學習視頻：第3章-二分類線性判別分析_嗶哩嗶哩_bilibili
西瓜書對應章節： 3.4

---

---

- 算法原理

- 損失函數推導

---- 投影后 ------

– 異類樣本中心盡可能遠

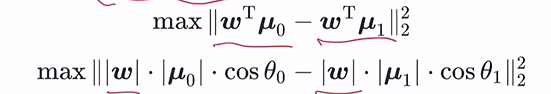
– 同類樣本方差盡可能小

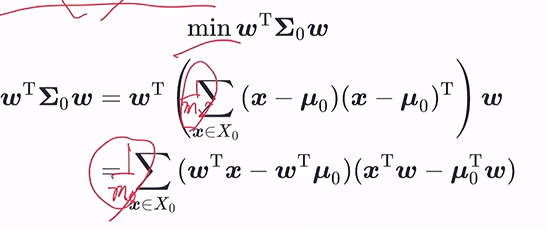
– 綜合

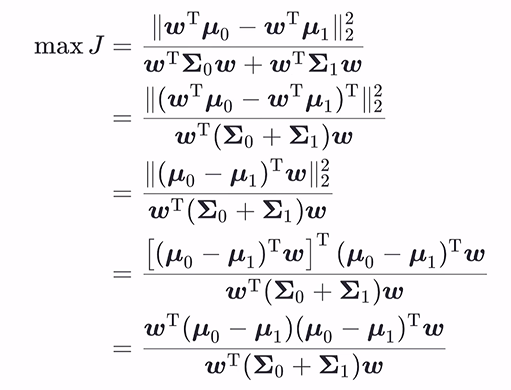
分母為 同類樣本之間的關系，分子為異類樣本之間的關系，使分子盡量小（同類樣本方差盡可能小），分母盡量大（異類樣本中心盡量遠），則有 $Max$ $J$

---

知識點補充 - 二范數

二范數（2-norm）詳解

定義

對于一個n維歐幾里得空間中的向量 $\mathbf{x}=[x_1,x_2,\dots ,x_n{]}^{\text{T}}$，其二范數定義為：
$\Vert \mathbf{x}{\Vert }_2=\sqrt{x_1^2+x_2^2+?+x_n^2}=\sqrt{{\mathbf{x}}^{\text{T}}\mathbf{x}}$

幾何意義

在二維或三維空間中，二范數表示向量末端到原點的歐幾里得距離。例如，在二維空間中，向量 $\mathbf{x}=[x_1,x_2{]}^{\text{T}}$ 的二范數表示為：
$\Vert \mathbf{x}{\Vert }_2=\sqrt{x_1^2+x_2^2}$
這正是勾股定理的直接應用，表示向量 $\mathbf{x}$ 在平面上的長度。

性質

1. 非負性：對于所有向量 $\mathbf{x}，\Vert \mathbf{x}{\Vert }_2\ge 0，且\Vert \mathbf{x}{\Vert }_2=0當且僅當\mathbf{x}=0$。
2. 齊次性：對于所有向量 $\mathbf{x}$ 和所有標量 $c$，$\Vert c\mathbf{x}{\Vert }_2=|c|\Vert \mathbf{x}{\Vert }_2$。
3. 三角不等式：對于所有向量 $\mathbf{x}$ 和 $\mathbf{y}$，$\Vert \mathbf{x}+\mathbf{y}{\Vert }_2\le \Vert \mathbf{x}{\Vert }_2+\Vert \mathbf{y}{\Vert }_2$。

應用

二范數在數值分析、機器學習、信號處理等領域有廣泛應用。例如，在機器學習中，二范數常用于正則化項，以防止模型過擬合；在信號處理中，二范數用于衡量信號的能量。

示例

考慮向量 $\mathbf{x}=[3,4{]}^{\text{T}}$，其二范數為：
$\Vert \mathbf{x}{\Vert }_2=\sqrt{3^2+4^2}=\sqrt{9+16}=\sqrt{25}=5$
這表示向量 (\mathbf{x}) 在二維空間中的長度為5。

---

---

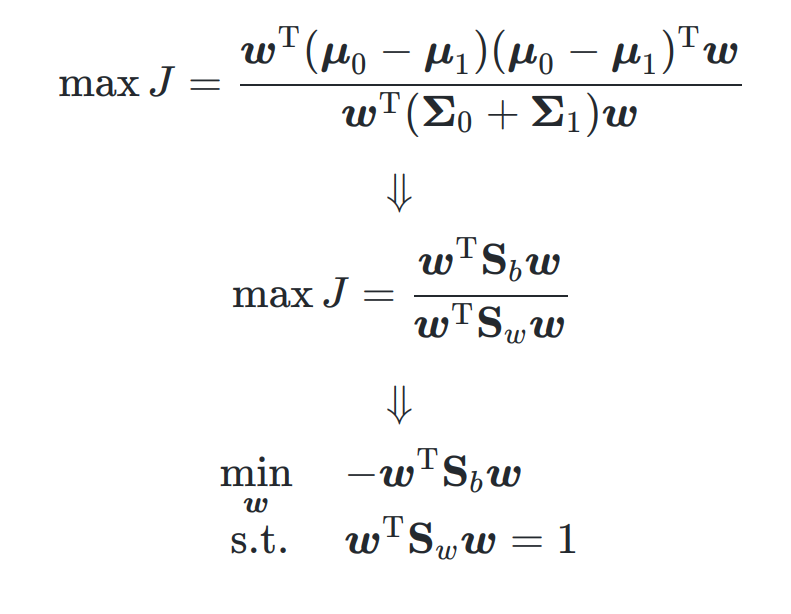
求解 w

• 利用 拉格朗日乘子法 對該式子進行轉化
  

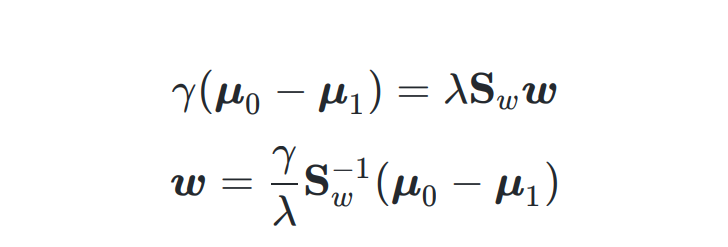
知識點補充 - 廣義瑞利商

廣義瑞利商（Generalized Rayleigh Quotient）是一種在數學和工程中廣泛使用的概念，特別是在信號處理、模式識別和最優化問題中。它是經典瑞利商的推廣，用于衡量向量在不同矩陣（通常是對稱正定矩陣）下的分布情況。

定義

廣義瑞利商的形式如下：

$R(\mathbf{w})=\frac{{\mathbf{w}}^{?}\mathbf{Aw}}{{\mathbf{w}}^{?}\mathbf{Bw}}$

其中，$\mathbf{A}$ 和 $\mathbf{B}$ 是對稱矩陣，$\mathbf{B}$ 通常是正定的，$\mathbf{w}$ 是一個非零向量。

解釋

• $\mathbf{A}$ 通常表示待優化的問題中涉及的矩陣，例如散布矩陣或相關矩陣。
• $\mathbf{B}$ 通常表示一個約束矩陣，比如在模式識別中的類內散布矩陣或協方差矩陣。
• $\mathbf{w}$ 是我們要尋找的向量，使得廣義瑞利商 $R(\mathbf{w})$ 達到最大或最小。

應用

1. 線性判別分析 (LDA)：
   在模式識別中，LDA 通過最大化類間散布矩陣$\mathbf{S}$與類內散布矩陣 ${\mathbf{S}}_w$的廣義瑞利商來找到最優的投影方向：
   $R(\mathbf{w})=\frac{{\mathbf{w}}^{?}{\mathbf{S}}_b\mathbf{w}}{{\mathbf{w}}^{?}{\mathbf{S}}_w\mathbf{w}}$

2. 特征值問題：
   廣義瑞利商的極值問題可以轉化為廣義特征值問題，解決矩陣 $\mathbf{Aw}=\lambda \mathbf{Bw}$ 中的特征值 $\lambda$ 和特征向量 $\mathbf{w}$。

3. 振動分析：
   在結構工程和機械工程中，用于分析系統在不同狀態下的振動模式。

優化廣義瑞利商

求解廣義瑞利商最大化或最小化的問題通常涉及求解廣義特征值問題：
$\mathbf{Aw}=\lambda \mathbf{Bw}$
其中，$\lambda$ 是廣義瑞利商的極值。

通過解這個特征值問題，可以得到使廣義瑞利商達到極值的 $\mathbf{w}$ 和對應的特征值 $\lambda$。

---