前言
排序作為生產環境中常見的需求之一,對整個產品有舉足輕重的影響,可以說使用一個合適的排序算法是業務邏輯中比較重要的一部分。今天我們就來介紹常見的排序算法以及實現
排序
所謂排序無非就是按照特定的規則對一組數據就行順序化。
常見的排序有升序和降序。
對于數字類型的數據常見的規則是按照其大小排序。如果學過Java的朋友應該知道,Java引入了對象的概念,對象的排序規則一般需要程序員自己定義,實現Comparable或者Comparator接口,在在接口內部實現排序的邏輯
除排序本身的定義外,我們還需要了解一點關于排序的性質
- 穩定性:當“大小”一致的兩個數據應該如何規定兩者的順序呢?比如一個班級中有兩位考100分的同學,我們應該如何規定兩者的順序呢?顯然,一個常見的想法是誰先交卷誰是第一名。這種保證“交卷順序”的排序算法,我們可以描述為穩定的排序算法。穩定性即保證排序后“大小”一致的數據順序與排序前一致
- 內/外排序:這是一組相對的概念。內部排序要求排序的數據全部在內存中完成排序。外部排序要求排序的數據在硬盤內存中移動來完成排序,常用于數據量巨大或者內存不夠的時候使用。
常見的排序算法
常見的排序算法有比較類的排序:冒泡排序,插入排序,希爾排序,選擇排序,堆排序,快速排序,歸并排序
非比較類的排序:基數排序,計數排序,桶排序
下面我們就一個一個來了解上述算法的思想和代碼實現,以下筆者均以排升序舉例。
筆者在排序算法的實現中可能會用到交換算法,在這里先實現,后面不在介紹
//交換元素
void swap(int* p1, int* p2) {int tmp = *p1;*p1 = *p2;*p2 = tmp;
}這里是一個簡答的交換,我們只是把它封裝一層,實現代碼的復用
冒泡排序
冒牌排序,思路是相鄰兩個數據就行比較,遍歷一遍為一趟排序。一趟排序后可以保證本趟最大值位于合適的位置。由此,每趟排序后下一趟的比較次數可以優化。也可以定義一個標記,如果本趟沒有交換,整個序列均有序
實現
//冒泡排序
void BubbleSort(int* a, int n);void BubbleSort(int* a, int n)
{for (int y = 0; y < n - 1; y++){int flag = 1;int len = n - y;for (int i = 0; i < len - 1; i++){if (a[i] > a[i + 1]){swap(a + i + 1, a + i);flag = 0;}}if (flag) return;}
}1. 冒泡排序是一種非常容易理解的排序
2. 時間復雜度:O(N^2)
3. 空間復雜度:O(1)
4. 穩定性:穩定
插入排序
插入排序,思路是假設前n個數據已經有序,第n+1個數據插入到有序的序列中。這個算法的適應性很強
實現
//插入排序
void InsertSort(int* a, int n);void InsertSort(int* a, int n)
{for (int i = 0; i < n - 1; i++){int end = i;int tmp = a[end + 1];while (end >= 0){if (tmp < a[end]){a[end + 1] = a[end];end--;}else{break;}}a[end + 1] = tmp;}
}1. 元素集合越接近有序,直接插入排序算法的時間效率越高
2. 時間復雜度:O(N^2)
3. 空間復雜度:O(1)
4. 穩定性:穩定
?
希爾排序
希爾排序是對插入排序的優化。插入排序的缺陷在于,在將降序排序成升序時,后面的較小值越來越難以移動到前面的位置,因為移動的次數由1,2,3……往上自增。希爾排序的優化在于增加跨度的方讓序列更快的接近有序。 引入一個gap變量,即數據分為gap組,以組為單位進行插入排序。不斷改變gap的值,有兩個常用的gap算式 gap=gap/2 和 gap=gap/3+1。這兩個算式均可以保證最后一次gap為1,即保證最后一次希爾排序轉換為插入排序(此時序列接近有序,前面介紹插入排序時介紹插入排序的適應性很強,表現在排序一個接近有序的序列時效率很高)。當然也可以自定義gap算式,但是需要保證gap最后一次的取值是1
實現
//希爾排序
void ShellSort(int* a, int n);void ShellSort(int* a, int n)
{int gap = n;while (gap > 1){gap = gap / 3 + 1;int i = 0;while (i < gap){int y = i;while (1){if (y >= n || y + gap >= n)break;if (a[y + gap] < a[y]) {int x = y;int tmp = a[y + gap];while (x >= 0 && tmp < a[x]){a[x + gap] = a[x];x -= gap;}a[x + gap] = tmp;}y += gap;}i++;}}
}1. 可以理解為gap!=1時是預排序,gap=1時是插入排序。希爾排序是對插入排序的優化
2. 時間復雜度:O(N^1.3)
3. 空間復雜度:O(1)
4. 穩定性:不穩定
選擇排序
選擇排序是一個比較簡單的排序算法,主要的邏輯就是每一趟找出最小的值,和本趟開頭位置的元素呼喚。這里可以有一點優化,就是在一趟遍歷的時候,同時找最大值和最小值。
實現
這里我們提供兩個版本的實現,優化和非優化的版本(說是優化,其實性能并沒有提升多少)
//選擇排序
void SelectSort(int* a, int n);//優化版,同時選擇大小
void SelectSort1(int* a, int n);//只選擇小void SelectSort1(int* a, int n)//取小交換
{for (int y = 0; y < n - 1; y++) {int i = y;int tmp = y + 1;for (; tmp < n; tmp++){if (a[tmp] < a[i])i = tmp;}swap(a + i, a + y);}
}
void SelectSort(int* a, int n)//優化,取大小交換
{int begin = 0;int end = n - 1;while (begin < end){int min = begin;int max = begin;for (int i = begin + 1; i <= end; i++){if (a[i] < a[min])min = i;else if (a[i] > a[max])max = i;}swap(a + begin, a + min);if (begin == max)max = min;swap(a + end, a + max);begin++;end--;}
}1. 直接選擇排序思考非常好理解,但是效率不是很好。實際中很少使用
2. 時間復雜度:O(N^2)
3. 空間復雜度:O(1)
4. 穩定性:不穩定
?
堆排序
堆排序是依賴于堆這個數據結構實現的一種排序算法。什么是堆這里不再展開。我們想要用堆排序算法實現升序,需要用所有的數據建立一個大根堆,然后不斷的pop堆頂的元素與堆末尾(邏輯上是堆,實際上是數組)元素交換,調整堆……知道堆中只剩一個元素,此時排序完成。
實現
//堆排序
void HeapSort(int* a, int n);void xiangXiaTiaoZheng(int* arr, int pr, int k) {//向下調整int ch = pr * 2 + 1;while (ch < k) {if (ch + 1 < k && arr[ch + 1] > arr[ch]) ch++;if (arr[ch] > arr[pr]) {swap(arr + ch, arr + pr);pr = ch;ch = pr * 2 + 1;}else return;}
}
void jianDui(int* arr, int k)//建堆
{for (int i = (k - 2) / 2; i >= 0; i--) {xiangXiaTiaoZheng(arr, i, k);}
}
void HeapSort(int* a, int n)
{jianDui(a, n);int end = n - 1;while (end > 0) {swap(a, a + end);xiangXiaTiaoZheng(a, 0, end);end--;}
}1. 堆排序使用堆來選數,效率就高了很多(topK問題)。向下調整建堆的算法要比向上調整建堆的算法效率高
2. 時間復雜度:O(N*logN)
3. 空間復雜度:O(1)
4. 穩定性:不穩定
?
快速排序
快速排序的思想是以每趟開始的元素為基準,將大于基準的元素放在基準數的右邊,將小于基準的元素放在基準的左邊,此時可以保證基準位于合適的位置。然后再分別處理基準的左半邊和右半邊,知道所有的元素都位于合適的位置上。
我們可以將實現分類為遞歸實現和非遞歸實現
遞歸實現
遞歸實現的大體邏輯是相同的,只不過在每一趟的實現有可以分為不同的版本。這里我們介紹三種不同的實現方式——hoare版本、挖坑版本、雙指針版本
hoare版本
這里單趟的邏輯是以左側開始位置的元素為基準元素,右邊開始向左遍歷在第一個小于基準元素的位置停下,左邊開始向右遍歷在第一個大于基準元素的位置停下,交換左右的元素,以上邏輯循環直到左右相遇,退出循環再交換相遇位置和起始位置的元素。
void QuickSort(int* a, int begin, int end);//hoare版本void QuickSort(int* a, int begin, int end)//hoare版本
{if (begin >= end)return;/*if ((end - begin + 1) < 10){InsertSort(a + begin, end - begin + 1);return;}int z = QuZhong(a, begin, end);swap(a + begin, a + z);*/int tmp = a[begin];int left = begin;int right = end;while (left < right){while (left < right && a[right] >= tmp){right--;}while (left < right && a[left] <= tmp){left++;}swap(a + left, a + right);}swap(a + begin, a + left);QuickSort(a, begin, left - 1);QuickSort(a, left + 1, end);
}此版本是最初實現快速排序是使用的版本。
為了方便理解,后面再開發出雙指針法和挖坑法
挖坑版本
挖坑法單趟的思路是以左側開始位置的元素為基準元素,同時將左側開始位置的元素記錄到tmp中,設置此位置為坑。右邊開始向左遍歷在第一個小于基準元素的位置停下,將此位置的元素放到坑中,再將此位置設置為坑。將左邊開始向右遍歷在第一個大于基準元素的位置停下,將此位置的元素放到坑中,再將此位置設置為坑。以上邏輯循環直到左右相遇,退出循環,此時相遇的位置是坑位,將tmp添入坑位中
void QuickSort1(int* a, int begin, int end);//挖坑法版本void QuickSort1(int* a, int begin, int end)
{if (begin >= end)return;/*if ((end - begin + 1) < 10){InsertSort(a + begin, end - begin + 1);return;}int z = QuZhong(a, begin, end);swap(a + begin, a + z);*/int tmp = a[begin];int tmpi = begin;int left = begin;int right = end;while (left < right){while (left < right && a[right] >= tmp){right--;}if (left < right){swap(a + tmpi, a + right);tmpi = right;left++;}while (left < right && a[left] <= tmp){left++;}if (left < right){swap(a + tmpi, a + left);tmpi = left;right--;}}QuickSort1(a, begin, left - 1);QuickSort1(a, left + 1, end);
}雙指針版本
以本趟開始位置的元素為基準元素。定義兩個指針變量,第一個指針prev指向本趟開始的元素,第二個指針cut指向本趟的第二個元素。如果cut指向的元素小于等于基準,則prev指針+1,prev與cut元素交換,cut指針+1:否則cut指針+1。直到cut指向空指針,退出循環,將基準元素與prev指向的元素互換。
void QuickSort2(int* a, int begin, int end);//雙指針版本void QuickSort2(int* a, int begin, int end)
{if (begin >= end)return;/*if ((end - begin + 1) < 10){InsertSort(a + begin, end - begin + 1);return;}int z = QuZhong(a, begin, end);swap(a + begin, a + z);*/int prev = begin;int cut = begin + 1;int tmp = a[begin];while (cut <= end){while (cut <= end && a[cut] <= tmp){prev++;cut++;}while (cut <= end && a[cut] > tmp){cut++;}if (cut <= end){prev++;swap(a + prev, a + cut);}}swap(a + begin, a + prev);QuickSort2(a, begin, prev - 1);QuickSort2(a, prev + 1, end);
}非遞歸實現
遞歸版本在內存的開銷上有可能會造成棧溢出,此時改成非遞歸是常見的需求。該非遞歸的核心思路就是用棧模擬遞歸的過程,利用棧存儲關鍵的信息。
非遞歸需要依賴于棧這個數據結構,這里也不在展開
棧:
#pragma once
#include <stdio.h>
#include <stdlib.h>// 支持動態增長的棧
typedef int STDataType;
typedef struct Stack
{STDataType* _a;int _top; // 棧頂int _capacity; // 容量
}Stack;// 初始化棧
void StackInit(Stack* ps);
// 入棧
void StackPush(Stack* ps, STDataType data);
// 出棧
void StackPop(Stack* ps);
// 獲取棧頂元素
STDataType StackTop(Stack* ps);
// 獲取棧中有效元素個數
int StackSize(Stack* ps);
// 檢測棧是否為空,如果為空返回非零結果,如果不為空返回0
int StackEmpty(Stack* ps);
// 銷毀棧
void StackDestroy(Stack* ps);#define _CRT_SECURE_NO_WARNINGS 1
#include "Stack.h"void StackInit(Stack* ps)
{ps->_a = NULL;ps->_top = -1;ps->_capacity = 0;
}void StackPush(Stack* ps, STDataType data)
{if (ps->_capacity == 0) {ps->_a = (STDataType*)malloc(sizeof(STDataType) * 4);//默認初始化長度為4ps->_capacity = 4;ps->_top = 0;}else if (ps->_top == ps->_capacity){ps->_capacity *= 2;ps->_a = (STDataType*)realloc(ps->_a, sizeof(STDataType) * ps->_capacity);//默認擴容至原先的兩倍}(ps->_a)[ps->_top++] = data;
}void StackPop(Stack* ps)
{if (ps->_top <= 0) return;ps->_top--;
}STDataType StackTop(Stack* ps) {if (ps->_top <= 0) return 0;return (ps->_a)[--ps->_top];
}int StackSize(Stack* ps)
{return ps->_top;
}int StackEmpty(Stack* ps)
{if (ps->_top <= 0) return 1;return 0;
}void StackDestroy(Stack* ps)
{free(ps->_a);ps->_a = NULL;ps = NULL;
}void QuickSortNonR(int* a, int begin, int end);//非遞歸版本void QuickSortNonR(int* a, int begin, int end) //非遞歸版本
{Stack sk;StackInit(&sk);StackPush(&sk, end);StackPush(&sk, begin);while (!StackEmpty(&sk)){int left = StackTop(&sk);int right = StackTop(&sk);int rembegin = left;int remend = right;int tmp = a[left];while (left < right){while (left < right && a[right] >= tmp){right--;}while (left < right && a[left] <= tmp){left++;}swap(a + left, a + right);}swap(a + rembegin, a + left);if (left + 1 < remend) {StackPush(&sk, remend);StackPush(&sk, left + 1);}if (rembegin < left - 1) {StackPush(&sk, left - 1);StackPush(&sk, rembegin);}}StackDestroy(&sk);
}優化
在此基礎上可以對快速排序展開兩個簡單的優化
- 小區間優化(當排序元素小于10可以轉換為插入排序,減少遞歸的深度,減少開銷)
將代碼中注釋的部分放開即可以實現小區間優化
- 三數取中(避免出現向一邊遞歸,算法退化為N^2的情況)
int QuZhong(int* arr, int first, int last)//優化,三數取中
{int z = (first + last) / 2;int a = arr[first];int b = arr[z];int c = arr[last];if (b > c){if (c > a)return last;else{if (a < b)return first;elsereturn z;}}else{if (b > a)return z;else{if (a < c)return first;elsereturn last;}}
}1. 快速排序整體的綜合性能和使用場景都是比較好的,所以才敢叫快速排序
2. 時間復雜度:O(N*logN)
3. 空間復雜度:O(logN)
4. 穩定性:不穩定
?
歸并排序
歸并排序是一種典型的分治思想,將大問題拆分成不能再分割的小問題。思路在將待排序不斷對半分割分割,分割到不能再分割時將相鄰兩個組合并為一個有序的大組,再將兩個相鄰的兩個大組合并為一個有序的大大組……
這里依然是提供兩個版本的實現,遞歸版和非遞歸版
這里非遞歸的實現,是直接將單個元素視為遞歸下來不能再分割的最小單位,實現往上回歸的部分
//歸并排序
void MergeSort(int* a, int begin, int end);//遞歸版本
void MergeSortNonR(int* a, int begin, int end);//非遞歸版本void MergeSort(int* a, int begin, int end)//歸并排序
{int n = end - begin + 1;if (n < 2) return;int min = begin + n / 2;MergeSort(a, begin, min - 1);MergeSort(a, min, end);int* arr = (int*)malloc(sizeof(int) * n);int left = begin;int right = min;int i = 0;while (left < min && right <= end){if (a[left] < a[right]){arr[i++] = a[left++];}else{arr[i++] = a[right++];}}if (left == min) {while (right <= end) {arr[i++] = a[right++];}}else{while (left < min) {arr[i++] = a[left++];}}i = 0;for (int y = begin; y <= end; y++){a[y] = arr[i++];}free(arr);
}void MergeSortNonR(int* a, int begin, int end)//非遞歸版本
{int gap = 1;int n = end - begin + 1;int* arr = (int*)malloc(sizeof(int) * n);while (gap < n){for (int y = 0; y < n; y += gap * 2){int left = y;int right = y + gap;if (right >= n) {for (int z = left; z < n; z++){arr[z] = a[z];}break;}int i = y;int end1 = y + gap;int end2 = right + gap;if (end2 >= n)end2 = n;while (left < end1 && right < end2){if (a[left] < a[right]){arr[i++] = a[left++];}else{arr[i++] = a[right++];}}if (left == end1) {while (right < end2) {arr[i++] = a[right++];}}else{while (left < end1) {arr[i++] = a[left++];}}}for (int z = 0; z < n; z++){a[z] = arr[z];}gap *= 2;}free(arr);
}1. 歸并的缺點在于需要O(N)的空間復雜度,歸并排序的思考更多的是解決在磁盤中的外排序問題。
2. 時間復雜度:O(N*logN)
3. 空間復雜度:O(N)
4. 穩定性:穩定
?
計數排序
計數排序是一種非比較的排序,適用于對整數進行排序。思想是得到序列中的最大值和最小值,計算得到中間最多有多少個元素,遍歷一遍序列,將元素映射到計數表中,再從計數表中依次讀取出元素。
//計數排序
void CountSort(int* a, int n);void CountSort(int* a, int n)
{int min = a[0];int max = a[0];for (int i = 1; i < n; i++){if (a[i] < min)min = a[i];else if (a[i] > max)max = a[i];}int countN = max - min + 1;int* arr = (int*)calloc(countN, sizeof(int));for (int i = 0; i < n; i++){arr[a[i] - min]++;}int y = 0;for (int i = 0; i < countN&&y<n; i++){int sz = arr[i];while (sz--){a[y++] = i + min;}}
}1. 計數排序在數據范圍集中時,效率很高,但是適用范圍及場景有限。
2. 時間復雜度:O(MAX(N,范圍))
3. 空間復雜度:O(范圍)
4. 穩定性:穩定
桶排序和基數排序
桶排序和基數排序不常用,這里只簡單介紹思想不介紹具體實現
桶排序工作的原理是將數組分到有限數量的桶里。每個桶再分別排序,最后依次把各個桶中的記錄列出來記得到有序序列
基數排序是一種非比較型整數排序算法,其原理是將整數按位數切割成不同的數字,然后按每個位數分別比較
排序算法的比較
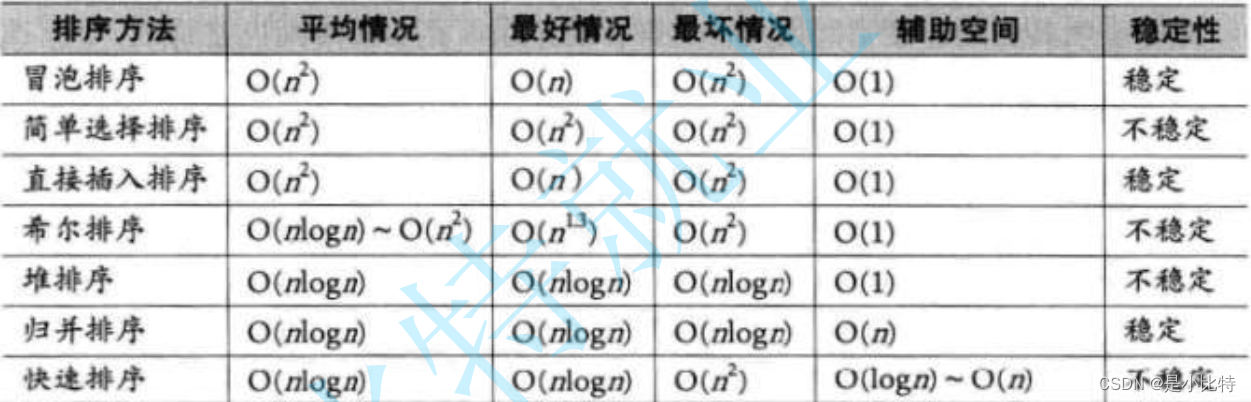
?
?
結語
排序這部分重點掌握不同算法的思想,把握一趟是如何實現的,其他每一趟都是一樣的思想
以上便是今天的全部內容。如果有幫助到你,請給我一個免費的贊。
因為這對我很重要。
編程世界的小比特,希望與大家一起無限進步。
感謝閱讀!



![[Cocos Creator] v3.8開發知識點記錄(持續更新)](http://pic.xiahunao.cn/[Cocos Creator] v3.8開發知識點記錄(持續更新))




五千字好文)
![C語言力扣刷題7——刪除排序鏈表中的重復元素 II——[快慢雙指針法]](http://pic.xiahunao.cn/C語言力扣刷題7——刪除排序鏈表中的重復元素 II——[快慢雙指針法])
輕松入門LangChain)








+AI繪畫,文生圖,TTS語音識別輸入,文檔分析)