AIM?— 圖像領域中 LLM 的對應物。盡管?iGPT?已經存在 2 年多了,但自回歸尚未得到充分探索。在本文中,作者表明,當使用 AIM 對網絡進行預訓練時,一組圖像數據集上的下游任務的平均準確率會隨著數據和參數的增加而線性增加。
要運行下面的代碼,請使用我的?Jupyter 筆記本
NSDT工具推薦:?Three.js AI紋理開發包?-?YOLO合成數據生成器?-?GLTF/GLB在線編輯?-?3D模型格式在線轉換?-?可編程3D場景編輯器?-?REVIT導出3D模型插件?-?3D模型語義搜索引擎?-?Three.js虛擬軸心開發包?-?3D模型在線減面?-?STL模型在線切割?
AIM 引入了兩個概念:
- 對于預訓練:AIM 引入了一種稱為 PrefixLM 的東西,它允許在下游任務期間進行雙向 attn 并進行預訓練而無需改變架構。
- 對于下游:Attentive Probing
在這篇博客中,我們將了解自注意力中的 Casual Masking 是什么,然后看看 PrefixLM 是如何設計的。
在閱讀這篇博客之前,我強烈建議你先觀看這個?nanoGPT 視頻教程?。
讓我們先加載所需的庫。
import math
import numpy as np
import torch
import torch.nn as nn
import fastcore.all as fc
from PIL import Image
from functools import partial
from torchvision.transforms import RandomResizedCrop, RandomHorizontalFlip, Compose, ToTensor, ToPILImageimport matplotlib.pyplot as plt
plt.style.use("bmh")
%matplotlib inline讓我們創建一個大小為 224x224 的圖像,其中補丁大小為 32
img_size = 224
patch_size = 321、加載并可視化圖像
我們加載并使用 coco val 數據。為了這個博客的目的,你可以從互聯網上挑選任何圖像。
imgs = fc.L(fc.Path("../coco/val2017/").glob("*.jpg"))
imgs(#5000) [Path('../coco/val2017/000000182611.jpg'),Path('../coco/val2017/000000335177.jpg'),Path('../coco/val2017/000000278705.jpg'),Path('../coco/val2017/000000463618.jpg'),Path('../coco/val2017/000000568981.jpg'),Path('../coco/val2017/000000092416.jpg'),Path('../coco/val2017/000000173830.jpg'),Path('../coco/val2017/000000476215.jpg'),Path('../coco/val2017/000000479126.jpg'),Path('../coco/val2017/000000570664.jpg')...]以下是論文中提到的標準變換:
def transforms():return Compose([RandomResizedCrop(size=224, scale=[0.4, 1], ratio=[0.75, 1.33], interpolation=2), RandomHorizontalFlip(p=0.5), ToTensor()])def load_img(img_loc, transforms):img = Image.open(img_loc)return transforms(img)load_img = partial(load_img, transforms=transforms())img = load_img(imgs[1])
img.shape #torch.Size([3, 224, 224])
coco val image
2、如何設置用于自動回歸的輸入數據?
圖像被分割成 K 個不重疊的塊網格,這些塊共同形成一個標記序列。由于圖像大小為 (224, 224),塊大小為 (32, 32),我們將獲得總共 7x7 =49 個塊。
imgp = img.unfold(1, patch_size, patch_size).unfold(2, patch_size, patch_size).permute((0, 3, 4, 1, 2)).flatten(3).permute((3, 0, 1, 2))
imgp.shape #torch.Size([49, 3, 32, 32])fig, ax = plt.subplots(figsize=(4, 4), nrows=7, ncols=7)
for n, i in enumerate(imgp):ax.flat[n].imshow(ToPILImage()(i))ax.flat[n].axis("off")
plt.show()
image to tokens
自回歸的設置方式如下:
- 對于 token 1 -> token 2 是預測
- 對于 token 1, 2 -> token 3 是預測
- 對于 token 1, 2, 3 -> token 4 是預測
- 對于 token 1, 2, 3, … n-1 -> token n 是預測。
因此輸入 token 將達到 [0, n-1],輸出 token 將達到 [1, n]
x = imgp[:-1]
y = imgp[1:]
x.shape, y.shape
#(torch.Size([48, 3, 32, 32]), torch.Size([48, 3, 32, 32]))例如,如果我們有 [0, 24] 以內的標記,則第 25 個標記是預測。在下圖中,RGB 圖像是輸入標記,用紅色邊框突出顯示的標記是該組輸入標記的預測標記。
prediction = 25
fig, ax = plt.subplots(figsize=(4, 4), nrows=7, ncols=7)
for n, i in enumerate(imgp):token = ToPILImage()(i)if n <prediction:ax.flat[n].imshow(token)elif n == prediction:new_size = (48, 48)new_im=np.zeros((48, 48, 3))new_im[:, :, 0] = 255new_im = Image.fromarray(np.uint8(new_im))box = tuple((n - o) // 2 for n, o in zip(new_size, token.size))new_im.paste(token, box)ax.flat[n].imshow(new_im, cmap="hsv")else:ax.flat[n].imshow(token.convert("L"), cmap="gray")ax.flat[n].axis("off")
plt.show()
前 N 個token和 GT token
3、如何將自注意力應用于輸入token
注意力不過是兩個矩陣之間的余弦相似度。但是在進行token級別預測時,網絡應該只看到那些到那時為止的標記,而不是那些之后的標記。例如,對于標記 25 的預測,我們應該只使用從 1 到 24 的標記,并丟棄從 26 到 49 的標記(在我們采用的示例中,我們有 49 個標記)。接下來我們將看看如何實現這一點。
在上面,我們得到 x 形狀為 (48, 3, 32, 32),y 形狀為 (48, 3, 32, 32)。y 是我們需要的輸出或基本事實,但我們將直接使用 PatchEmbed 將原始圖像轉換為標記,然后丟棄最終的標記。
首先執行?pip install git+https://git@github.com/apple/ml-aim.git?并導入必要的函數。
from aim.torch.layers import PatchEmbed, LayerNorm, SinCosPosEmbed, MLPpe = PatchEmbed(img_size=img_size, patch_size=patch_size, norm_layer=LayerNorm)
pePatchEmbed((proj): Conv2d(3, 768, kernel_size=(32, 32), stride=(32, 32))(norm): LayerNorm((768,), eps=1e-06, elementwise_affine=True)
)tokens = pe(img.unsqueeze(0))
tokens.shape #torch.Size([1, 49, 768])在 AIM 中,他們沒有使用類token。我們將添加 sincos 位置嵌入
scpe = SinCosPosEmbed(cls_token=False)pe = scpe(h=7, w=7, embed_dim=768)
pe.shape #torch.Size([49, 768])將這些位置嵌入添加到輸入token中
tokens = tokens+pe[None]
tokens.shape #torch.Size([1, 49, 768])我們現在將刪除最后一個標記,因為它沒有任何 Gt
tokens = tokens[:, :48, :]
tokens.shape #torch.Size([1, 48, 768])4、自注意力
Transformer 塊內會發生很多事情。但簡單來說,我們首先
- 規范化輸入
- 應用注意
- 應用 MLP
4.1 規范化
在 transformer 塊中,我們需要層規范化。層規范化通常在 token 級別完成,因此 token 之間沒有信息交換。
token_norms = LayerNorm(768)(tokens)
token_norms.mean((0, 2)),token_norms.var((0, 2))(tensor([ 0.0000e+00, -1.7385e-08, -2.1110e-08, -2.4835e-09, 1.8626e-09,1.2418e-09, 3.7253e-08, 2.3594e-08, 1.0555e-08, -9.9341e-09,1.2418e-08, -2.0800e-08, 1.9247e-08, -1.1797e-08, 6.7055e-08,1.1176e-08, 3.6632e-08, -3.6632e-08, -5.2465e-08, -2.4835e-08,-1.0245e-08, -1.5212e-08, 1.7385e-08, -3.3528e-08, -2.1110e-08,-2.2352e-08, 1.3039e-08, 1.8626e-08, -6.5193e-09, -2.7319e-08,-1.4280e-08, 2.1110e-08, -1.5522e-08, 3.1044e-09, 2.2041e-08,-9.3132e-10, 9.3132e-09, -2.8871e-08, -1.8626e-08, 3.1044e-09,2.6077e-08, 1.4901e-08, 1.1797e-08, -8.0715e-09, 4.8429e-08,-1.5522e-09, -4.1910e-08, -1.8316e-08], grad_fn=<MeanBackward1>),tensor([1.0013, 1.0013, 1.0013, 1.0013, 1.0013, 1.0013, 1.0013, 1.0013, 1.0013,1.0013, 1.0013, 1.0013, 1.0013, 1.0013, 1.0013, 1.0013, 1.0013, 1.0013,1.0013, 1.0013, 1.0013, 1.0013, 1.0013, 1.0013, 1.0013, 1.0013, 1.0013,1.0013, 1.0013, 1.0013, 1.0013, 1.0013, 1.0013, 1.0013, 1.0013, 1.0013,1.0013, 1.0013, 1.0013, 1.0013, 1.0013, 1.0013, 1.0013, 1.0013, 1.0013,1.0013, 1.0013, 1.0013], grad_fn=<VarBackward0>))4.2 MLP
在 MLP 中,每個 token [行] 也與 MLP 權重矩陣的每個 [列] 相乘。因此 token 之間沒有交互,這實際上意味著我們可以使用該網絡分別處理每個 token
mlp = MLP(in_features=768,hidden_features=768*4,act_layer=nn.GELU,drop=0.2,use_bias=False
)
mlpMLP((fc1): Linear(in_features=768, out_features=3072, bias=False)(act): GELU(approximate='none')(fc2): Linear(in_features=3072, out_features=768, bias=False)(drop): Dropout(p=0.2, inplace=False)
)mlp(token_norms).shape #torch.Size([1, 48, 768])4.3 因果注意力
注意力是我們使用查詢、鍵和值計算標記之間交互的唯一地方。但對于自回歸,過去的token不應該從未來學習。例如,如果我們預測token 5,我們應該只使用token 1、2、3、4 并丟棄來自 5 的所有token。在 Transformers 中,這是使用一種稱為因果注意力的東西實現的。我們將在本節中學習和理解它是什么。為了簡化理解,我們將只使用單個頭,而不是使用多個頭。
在注意力中,發生以下步驟
- 使用 mlp,獲取鍵、查詢和值。
- 在查詢和鍵之間應用自注意力(本質上是點積)。我們得到一個 qk 矩陣(49x49)。縮放值
- 應用 softmax
- qk 和 v 之間的自注意力。
# lets see a single head perform self-attention
B, T, C = token_norms.shape
head_size = 768
key = nn.Linear(C, head_size, bias=False)
query = nn.Linear(C, head_size, bias=False)
value = nn.Linear(C, head_size, bias=False)
k = key(token_norms)
q = query(token_norms)
v = value(token_norms)
scale_factor = 1 / math.sqrt(q.size(-1))
qk = q@k.transpose(-2, -1) * scale_factor #(B, T, 16) @ (B, 16, T) --. B, T, T
qk.shape #torch.Size([1, 48, 48])這個矩陣本質上會告訴你每個 token 之間的相互作用強度。
值會匯總來自所有其他 token 的每個 token 的信息。qk 的行 1 與值的所有列相乘,但 token1 應該只包含來自 token1 的信息,并丟棄所有其他信息。類似地,token2 應該只包含來自 token1 和 token2 的 qk 值,并丟棄所有其他值。如果你按照這個思路操作,我們理想情況下希望從矩陣的上三角中刪除所有值。
在注意力論文中,他們不是刪除,而是用 -inf 替換它。這是因為當應用 softmax 時,這些極小的值將變為零,因此不會產生任何影響。
tril = torch.tril(torch.ones(T,T))
plt.figure(figsize=(4, 4))
plt.imshow(tril.numpy())
plt.show()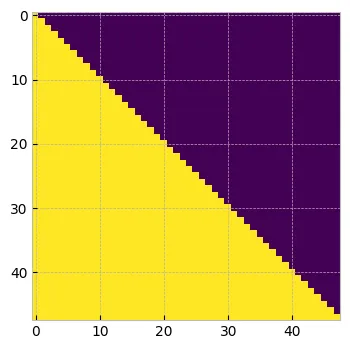
因果掩碼
qk = qk.masked_fill(tril==0, float("-inf"))
qk[0]tensor([[0.3354, -inf, -inf, ..., -inf, -inf, -inf],[0.3412, 0.3489, -inf, ..., -inf, -inf, -inf],[0.3663, 0.3698, 0.3422, ..., -inf, -inf, -inf],...,[0.9337, 0.9750, 0.9633, ..., 0.8890, -inf, -inf],[0.8462, 0.8887, 0.8814, ..., 0.8392, 0.7537, -inf],[0.6571, 0.6705, 0.6382, ..., 0.5844, 0.5688, 0.6007]],grad_fn=<SelectBackward0>)qk = torch.softmax(qk, dim=-1)
qk[0]tensor([[1.0000, 0.0000, 0.0000, ..., 0.0000, 0.0000, 0.0000],[0.4981, 0.5019, 0.0000, ..., 0.0000, 0.0000, 0.0000],[0.3356, 0.3368, 0.3276, ..., 0.0000, 0.0000, 0.0000],...,[0.0216, 0.0225, 0.0222, ..., 0.0206, 0.0000, 0.0000],[0.0211, 0.0220, 0.0219, ..., 0.0210, 0.0192, 0.0000],[0.0211, 0.0214, 0.0207, ..., 0.0196, 0.0193, 0.0199]],grad_fn=<SelectBackward0>)plt.figure(figsize=(4, 4))
plt.imshow(qk.detach().numpy()[0])
plt.show()
使用因果掩碼的注意力矩陣
現在,當我們用值進行相乘時,只有到那時為止的token才會共享信息。
attn = qk@v
attn.shape #torch.Size([1, 48, 768])這個注意力通過線性和 dropout 層傳播。
proj = nn.Linear(768, 768, bias=False)
tokens = proj(attn)
tokens.shape #torch.Size([1, 48, 768])Transformers 內部有一些跳躍連接和其他 MLP 塊用于穩定訓練,但這本質上是 Transformer 塊中發生的事情
5、PrefixLM
從上面我們可以看出,在自回歸預訓練時,我們應用了因果掩碼,而在微調時,如果我們刪除因果掩碼,我們正在進行雙向自我注意。這種差異導致微調時的性能低于標準。
為了解決這個問題,論文中的作者建議將序列的初始標記(稱為前綴)視為預測剩余補丁的上下文。因此,對初始 K 個標記應用雙向自我注意,并且不考慮對這些標記的預測。對于剩余的標記,我們將執行如上所述的因果掩碼。讓我們看看這是如何做到的。
假設我們考慮 k=25。我們將獲得 N 個補丁的掩碼
K = 25
mask = torch.ones(B, tokens.shape[1]).to(torch.bool)
mask[:, :K] = 0
print(mask.shape) #torch.Size([1, 48])
masktensor([[False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True]])prefix_mask = (~mask).unsqueeze(1).expand(-1, tokens.shape[1], -1).bool()
print(prefix_mask.shape)
prefix_mask[0] #torch.Size([1, 48, 48])tensor([[ True, True, True, ..., False, False, False],[ True, True, True, ..., False, False, False],[ True, True, True, ..., False, False, False],...,[ True, True, True, ..., False, False, False],[ True, True, True, ..., False, False, False],[ True, True, True, ..., False, False, False]])plt.figure(figsize=(4, 4))
plt.imshow(prefix_mask.numpy()[0])
plt.show()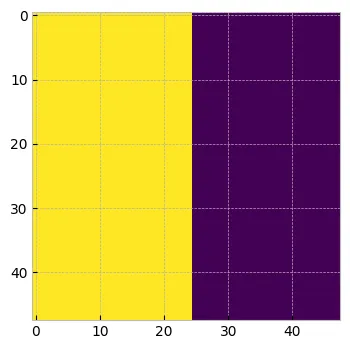
PrefixLM
我們現在將定義 attn_mask,其上限訓練值為零
attn_mask = torch.ones(1, tokens.shape[1], tokens.shape[1], dtype=torch.bool).tril(diagonal=0)
print(attn_mask.shape) #torch.Size([1, 48, 48])
plt.figure(figsize=(4, 4))
plt.imshow(attn_mask.numpy()[0])
plt.show()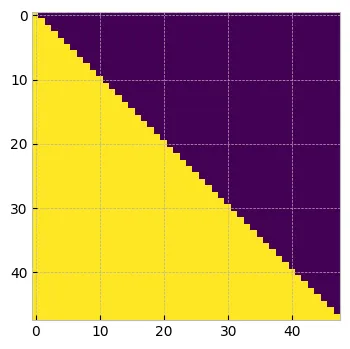
attn_mask = torch.logical_or(attn_mask, prefix_mask)
print(attn_mask.shape) #torch.Size([1, 48, 48])
plt.figure(figsize=(4, 4))
plt.imshow(attn_mask.numpy()[0])
plt.show()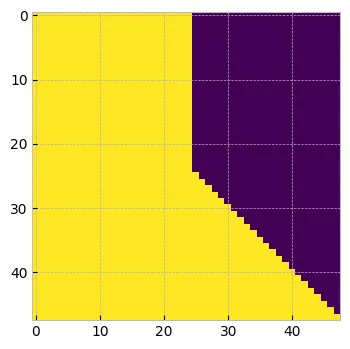
最終的因果掩碼
上述 attn_mask 將確保對于前 25 個標記我們將進行雙向自注意,并且對于剩余的標記應用 causual_masking。
qk = qk.masked_fill(attn_mask==0, float("-inf"))
print(qk.shape) #torch.Size([1, 48, 48])
qk[0]tensor([[1.0000, 0.0000, 0.0000, ..., -inf, -inf, -inf],[0.4981, 0.5019, 0.0000, ..., -inf, -inf, -inf],[0.3356, 0.3368, 0.3276, ..., -inf, -inf, -inf],...,[0.0216, 0.0225, 0.0222, ..., 0.0206, -inf, -inf],[0.0211, 0.0220, 0.0219, ..., 0.0210, 0.0192, -inf],[0.0211, 0.0214, 0.0207, ..., 0.0196, 0.0193, 0.0199]],grad_fn=<SelectBackward0>)qk = torch.softmax(qk, dim=-1)
qk[0]tensor([[0.1017, 0.0374, 0.0374, ..., 0.0000, 0.0000, 0.0000],[0.0626, 0.0628, 0.0380, ..., 0.0000, 0.0000, 0.0000],[0.0534, 0.0535, 0.0530, ..., 0.0000, 0.0000, 0.0000],...,[0.0217, 0.0218, 0.0217, ..., 0.0217, 0.0000, 0.0000],[0.0213, 0.0213, 0.0213, ..., 0.0213, 0.0212, 0.0000],[0.0208, 0.0208, 0.0208, ..., 0.0208, 0.0208, 0.0208]],grad_fn=<SelectBackward0>)plt.figure(figsize=(4, 4))
plt.imshow(qk.detach().numpy()[0])
plt.show()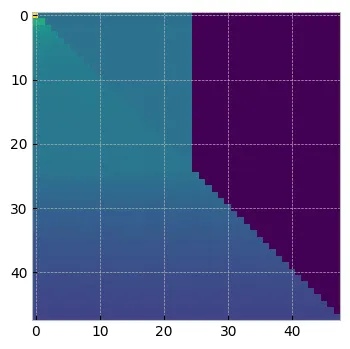
使用 PrefixLM 的最終 attn 矩陣
attn = qk@vtensor([[ 0.9102, 0.2899, -0.4562, ..., -0.0554, 0.2982, 1.4015],[ 0.9125, 0.2941, -0.4578, ..., -0.0558, 0.2949, 1.4056],[ 0.9135, 0.2954, -0.4594, ..., -0.0551, 0.2924, 1.4080],...,[ 0.8787, 0.3149, -0.5150, ..., -0.0829, 0.1735, 1.3375],[ 0.8820, 0.3152, -0.5220, ..., -0.0798, 0.1744, 1.3371],[ 0.8860, 0.3186, -0.5214, ..., -0.0759, 0.1729, 1.3319]],grad_fn=<SelectBackward0>)在 AIM 的背景下,他們沒有提到要使用什么 K 值。但我正在考慮我們可以在每次迭代中選擇一個隨機數。
在下一篇博客中,我們將看到如何使用 CIFAR 數據對 AIM 進行預訓練。
原文鏈接:AIM注意力和因果掩碼 - BimAnt

![[Cocos Creator] v3.8開發知識點記錄(持續更新)](http://pic.xiahunao.cn/[Cocos Creator] v3.8開發知識點記錄(持續更新))




五千字好文)
![C語言力扣刷題7——刪除排序鏈表中的重復元素 II——[快慢雙指針法]](http://pic.xiahunao.cn/C語言力扣刷題7——刪除排序鏈表中的重復元素 II——[快慢雙指針法])
輕松入門LangChain)








+AI繪畫,文生圖,TTS語音識別輸入,文檔分析)

)