每日一題——力扣144. 二叉樹的前序遍歷（舉一反三+思想解讀+逐步優化）五千字好文

一個認為一切根源都是“自己不夠強”的INTJ

個人主頁：用哲學編程-CSDN博客
專欄：每日一題——舉一反三
Python編程學習
Python內置函數

Python-3.12.0文檔解讀

?我的寫法：

代碼結構

時間復雜度

空間復雜度

總結

我要更強

代碼說明

時間復雜度

空間復雜度

哲學和編程思想

迭代與遞歸：

空間與時間的權衡：

抽象與具體化：

數據結構的選擇：

內存管理：

算法優化：

舉一反三

題目鏈接：https://leetcode.cn/problems/binary-tree-preorder-traversal/description/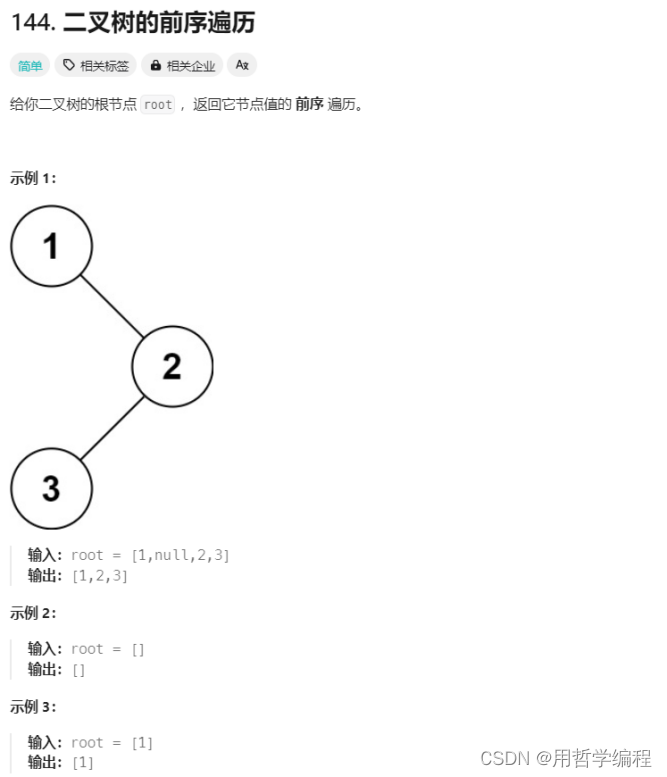

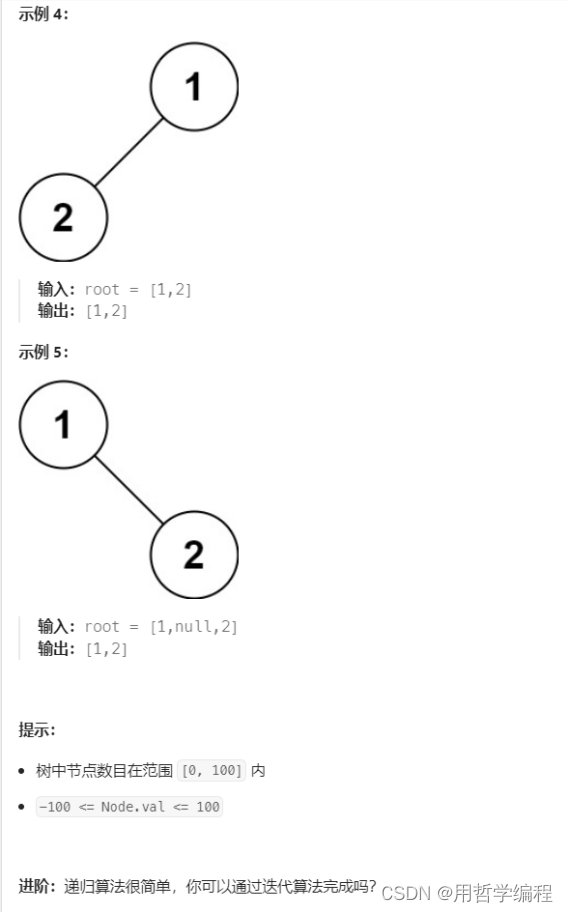
?我的寫法：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     struct TreeNode *left;*     struct TreeNode *right;* };*/
int TreeSize(struct TreeNode* root){return root == NULL ? 0 :1+TreeSize(root->left)+TreeSize(root->right);
}void perorder(struct TreeNode* root,int* a,int* pi){if(root==NULL)return;a[(*pi)++]=root->val;perorder(root->left,a,pi);perorder(root->right,a,pi);
}int* preorderTraversal(struct TreeNode* root, int* returnSize){*returnSize=TreeSize(root);int* a=(int*)malloc(*returnSize*sizeof(int));int i=0;perorder(root,a,&i);return a;
}

這段代碼實現了二叉樹的前序遍歷（Preorder Traversal），并返回一個包含遍歷結果的動態數組。下面是對這段代碼的專業點評：

代碼結構

TreeSize 函數：
- 該函數用于計算二叉樹的節點數量。它通過遞歸地遍歷左子樹和右子樹，并累加節點數來實現。如果根節點為空，則返回0；否則，返回1加上左子樹和右子樹的節點數。
perorder 函數：
- 這是一個遞歸函數，用于執行前序遍歷。前序遍歷的順序是：根節點 -> 左子樹 -> 右子樹。該函數將遍歷到的節點值存儲到數組?a?中，并通過引用傳遞的?pi?指針來更新數組索引。
preorderTraversal 函數：

這是主函數，負責分配返回數組的空間，調用?perorder?函數進行遍歷，并返回遍歷結果。它首先通過?TreeSize?函數確定返回數組的大小，然后分配相應大小的內存空間，并調用?perorder?函數填充數組。

時間復雜度

TreeSize 函數：O(n)，其中 n 是樹中的節點數。每個節點都被訪問一次。
perorder 函數：O(n)，同樣地，每個節點都被訪問一次。
preorderTraversal 函數：O(n)，因為它調用了?perorder?函數，而?perorder?函數的時間復雜度是 O(n)。

空間復雜度

TreeSize 函數：O(h)，其中 h 是樹的高度。在最壞的情況下，遞歸調用的棧深度等于樹的高度。
perorder 函數：O(h)，同樣地，遞歸調用的棧深度等于樹的高度。
preorderTraversal 函數：O(n)，因為需要分配一個大小為 n 的數組來存儲遍歷結果。此外，遞歸調用的棧空間也是 O(h)。

總結

這段代碼有效地實現了二叉樹的前序遍歷，并且時間復雜度和空間復雜度都是合理的。注意，空間復雜度中的 O(h) 部分是由于遞歸調用棧的使用，這在樹的高度較大時可能會成為一個問題。在實際應用中，需要考慮樹的平衡性以及可能的最大高度。

我要更強

為了優化時間復雜度和空間復雜度，我們可以考慮使用迭代方法而不是遞歸來實現前序遍歷。這樣可以避免遞歸調用棧的空間開銷，并且時間復雜度仍然是 O(n)，因為每個節點仍然只被訪問一次。

下面是使用迭代方法實現的完整代碼：

#include <stdlib.h>
#include <stdbool.h>struct TreeNode {int val;struct TreeNode *left;struct TreeNode *right;
};int* preorderTraversal(struct TreeNode* root, int* returnSize) {if (root == NULL) {*returnSize = 0;return NULL;}int* result = (int*)malloc(100 * sizeof(int)); // 假設最多100個節點，可根據實際情況調整struct TreeNode** stack = (struct TreeNode**)malloc(100 * sizeof(struct TreeNode*)); // 棧空間int top = -1; // 棧頂指針int index = 0; // 結果數組索引stack[++top] = root; // 根節點入棧while (top >= 0) {struct TreeNode* node = stack[top--]; // 出棧result[index++] = node->val; // 訪問節點// 由于前序遍歷是根-左-右，先右子樹入棧，再左子樹入棧if (node->right != NULL) {stack[++top] = node->right;}if (node->left != NULL) {stack[++top] = node->left;}}*returnSize = index; // 設置返回數組大小free(stack); // 釋放棧空間return result;
}

代碼說明

棧的使用：我們使用一個棧來模擬遞歸調用的過程。在迭代方法中，我們手動管理這個棧。
前序遍歷的順序：根節點首先被訪問，然后是左子樹，最后是右子樹。因此，我們在棧中先壓入右子樹，然后是左子樹，這樣在出棧時，左子樹會在右子樹之前被訪問。
內存管理：我們動態分配了棧和結果數組的空間。在函數結束前，我們釋放了棧的空間，但結果數組的空間由調用者負責釋放。

時間復雜度

O(n)：每個節點被訪問一次。

空間復雜度

O(h)：在最壞情況下，棧的大小等于樹的高度。在最好情況下（平衡樹），空間復雜度為 O(log n)。

這種方法在空間效率上優于遞歸方法，因為它避免了遞歸調用棧的空間開銷。然而，它仍然需要一個棧來模擬遞歸過程，因此在最壞情況下的空間復雜度仍然是 O(h)。如果樹非常不平衡，這可能會導致較高的空間使用。

哲學和編程思想

這些方法體現了以下哲學和編程思想：

迭代與遞歸：
- 遞歸是一種自我調用的方法，它依賴于調用棧來保存狀態。遞歸通常使得代碼更簡潔、易于理解，但在處理大量數據時可能會導致棧溢出。
- 迭代是一種循環結構，它通過顯式地管理狀態來避免遞歸的缺點。迭代通常更節省空間，因為它不需要額外的棧空間來保存中間狀態。
- 在上述代碼中，我們使用了迭代方法來實現前序遍歷，這體現了在空間效率和性能之間的權衡。
空間與時間的權衡：
- 在編程中，我們經常需要在空間復雜度和時間復雜度之間做出權衡。例如，使用額外的空間（如棧）來存儲中間結果，可以減少時間復雜度。
- 在迭代方法中，我們犧牲了一定的空間（棧空間）來減少遞歸調用棧的空間開銷，從而優化了整體的空間復雜度。
抽象與具體化：
- 抽象是指忽略問題的某些細節，專注于核心概念。在二叉樹遍歷中，我們抽象出了遍歷的順序（根-左-右），而不關心具體的實現細節。
- 具體化是指將抽象的概念轉化為具體的實現。在迭代方法中，我們將抽象的遍歷順序具體化為棧的操作，通過入棧和出棧來實現遍歷。
數據結構的選擇：
- 選擇合適的數據結構是編程中的一個重要決策。在二叉樹遍歷中，我們選擇了棧作為輔助數據結構，因為它可以有效地存儲和訪問節點的順序。
- 棧的先進后出（LIFO）特性非常適合模擬遞歸調用的過程，使得我們可以在迭代中實現與遞歸相同的前序遍歷順序。
內存管理：
- 在C語言中，內存管理是一個重要的編程實踐。我們手動分配和釋放內存，以避免內存泄漏和懸掛指針。
- 在代碼中，我們動態分配了棧和結果數組的空間，并在不再需要時釋放了棧的空間，這體現了良好的內存管理習慣。
算法優化：

算法優化是提高程序效率的關鍵。在迭代方法中，我們通過優化棧的使用順序（先右后左）來確保前序遍歷的正確性，這是一種算法層面的優化。

這些哲學和編程思想是解決復雜問題的基石，它們幫助我們在設計和實現代碼時做出明智的決策，以達到高效、可維護和可擴展的解決方案。

舉一反三

根據上述哲學和編程思想，以下是一些技巧和策略，可以幫助在面對類似問題時舉一反三：

理解問題本質：
- 在解決任何問題之前，首先要深入理解問題的本質。例如，在二叉樹遍歷問題中，理解前序遍歷的定義（根-左-右）是至關重要的。
- 技巧：將問題抽象為基本概念，然后從這些概念出發尋找解決方案。
選擇合適的數據結構：
- 根據問題的特點選擇合適的數據結構。例如，棧在處理需要逆序操作的問題時非常有用。
- 技巧：熟悉各種數據結構的特性，并能夠根據問題的需求靈活選擇。
迭代與遞歸的轉換：
- 學會將遞歸算法轉換為迭代算法，或者反之。這種轉換通常涉及到使用棧或隊列來模擬遞歸調用棧。
- 技巧：練習將遞歸算法重寫為迭代算法，以提高對這兩種方法的理解和應用能力。
空間與時間的權衡：
- 在設計算法時，考慮時間和空間的權衡。有時候，犧牲一些空間可以顯著提高時間效率。
- 技巧：評估不同解決方案的時間和空間復雜度，選擇最合適的平衡點。
內存管理：
- 在需要手動管理內存的編程語言中，如C語言，注意內存的分配和釋放。
- 技巧：養成良好的內存管理習慣，確保在不再需要內存時及時釋放。
算法優化：
- 不斷尋找算法優化的可能性。例如，通過改變數據結構的使用順序或方式來提高效率。
- 技巧：分析算法的瓶頸，嘗試不同的優化策略，如減少不必要的計算或改進數據訪問模式。
抽象與具體化：
- 學會將復雜問題抽象為簡單的模型，然后將這些模型具體化為可執行的代碼。
- 技巧：練習將問題分解為更小、更易于管理的部分，然后逐步構建解決方案。
代碼復用與模塊化：
- 在編寫代碼時，考慮代碼的復用性和模塊化。這有助于提高代碼的可維護性和可擴展性。
- 技巧：設計可重用的函數和類，將代碼分解為獨立的模塊。
測試與調試：