概述
作為一名軟件開發工程師,你對數據庫肯定再熟悉不過了。MySQL 作為主流的數據庫存儲系統,它在我們的業務開發中,有著舉足輕重的地位。在工作中,為了加速數據庫中數據的查找速度,我們常用的處理思路是,對表中的數據創建索引。那你是否考慮過,數據庫索引是如何實現的呢?底層使用的是什么數據結構和算法呢?
算法解析
思考的過程比結論重要,本章會盡量還原這個解決方案的思考過程,讓你知其然,并知其所以然。
1.解決問題的前提是定義清楚問題
如何定義清楚問題呢?除了對問題進行詳細的調研,還有一個辦法,那就是,通過對一些模糊的需求進行假設,來限定要解決的問題的范圍。
如果你對數據庫的操作非常了解,針對我們現在這個問題,你就能把索引的需求定義得非常清楚。但是,對于大部分軟件工程師來說,我們可能只了解一小部分常用的 SQL 語句,所以,我們這里假設要解決的問題,只包含這樣兩個常用的需求:
- 根據某個值查找數據,比如
select * from user where id = 1234。 - 根據區間來查找某些數據,比如
select * from user where id > 1234 and id < 2345。
除了這些功能性需求之外,這種問題往往還會涉及一些非功能性需求,比如安全、性能、用戶體驗等等。限于本章要討論的是數據結構和算法,對于非功能性需求,我們著重考慮性能方面的需求。性能方面的需求,我們主要考察時間和空間兩方面,也就是執行效率和存儲空間。
在執行效率方面,我們系統通過索引,查詢數據的效率盡可能地高;在存儲空間方面,我們希望索引不要消耗太多的內存空間。
2.嘗試用學過的數據結構解決這個問題
問題的需求大致定義清楚了,現在回想一下,能否利用已經學習過的數據結構解決這個問題呢?支持快速查詢、插入等操作的動態數據結構,我們學習過散列表、平衡二叉查找樹、跳表。
先來看散列表。散列表的查詢性能很好,時間復雜度是 O ( 1 ) O(1) O(1)。但是,散列表不支持按區間快速查找數據。所以,散列表不能滿足我們的需求。
再看下平衡二叉查找樹。盡管平衡二叉查找樹查詢的性能也很高,時間復雜度是 O ( l o g n ) O(logn) O(logn)。而且,對數進行中序遍歷,還可以得到一個從小到大的有序的數據序列,但仍然不足以支持按照區間快速查找數據。
最后看下跳表。跳表是在鏈表之上加上多層索引構成的。它支持快速插入、查找、刪除數據,對應的時間復雜度是 O ( l o g n ) O(logn) O(logn)。并且跳表也支持按區間快速查找數據。我們只需要定位區間的起點值對應在鏈表中的位置,然后從這個節點開始,順序遍歷鏈表,直到區間終點對應的結點為止,這期間遍歷得到的數據就是滿足區間值的數據。
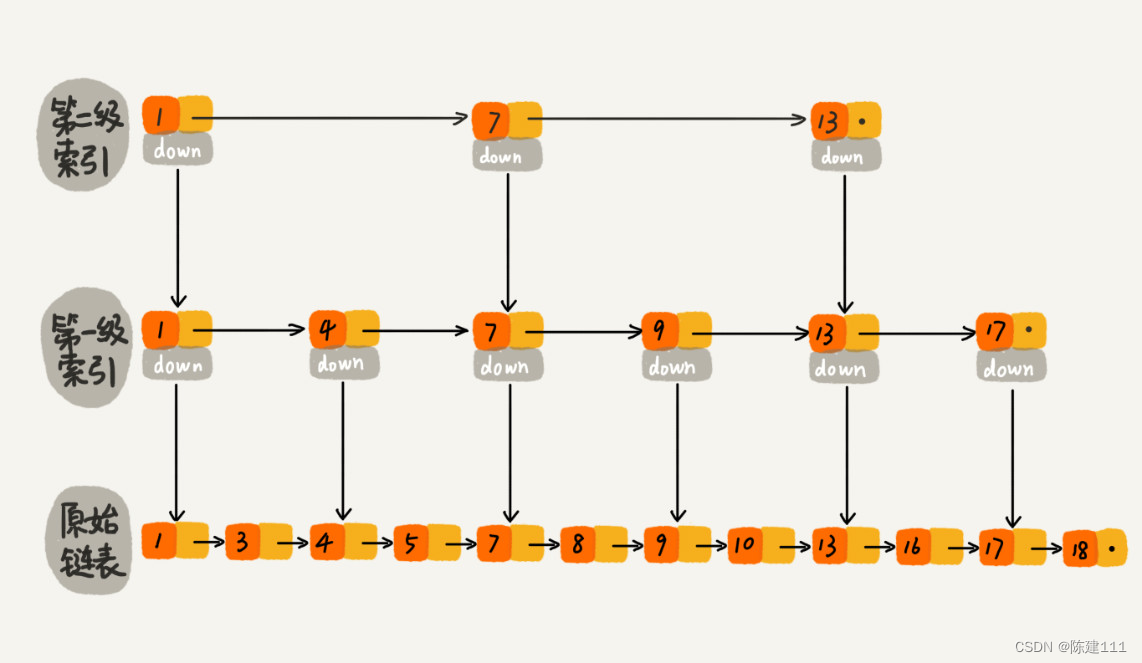
這樣看來,跳表是可以解決這個問題。實際上,數據庫索引所用到的數據結構跟跳表非常相似,叫作 B+ 樹。不過,它是通過二叉查找樹演化過來的,而非跳表。為了給你還原發明 B+ 樹的整個思考過程,所以,接下來,我還要從二叉查找樹將其,看它是如何一步一步被改造成 B+ 樹的。
改造二叉查找樹來解決這個問題
為了讓二叉查找樹支持按照區間來查找數據,我們可以對它進行這樣的改造:樹中的節點并不存儲數據本身,而是只是作為索引。此外,我們把每個葉子節點串在一條鏈表上,鏈表中的數據時從小到大有序的。經過改造之后的二叉樹,就像圖中這樣,看起來是不是很像跳表。

改造之后,如果我們要求某個區間的數據。我們只需要拿到區間的起始值,在樹中進行查找,當查找到某個葉子節點后,我們再順著鏈表往后遍歷,直到鏈表中的節點數據值大于區間的終止值為止。所有遍歷的數據,就是符合區間值的所有數據。
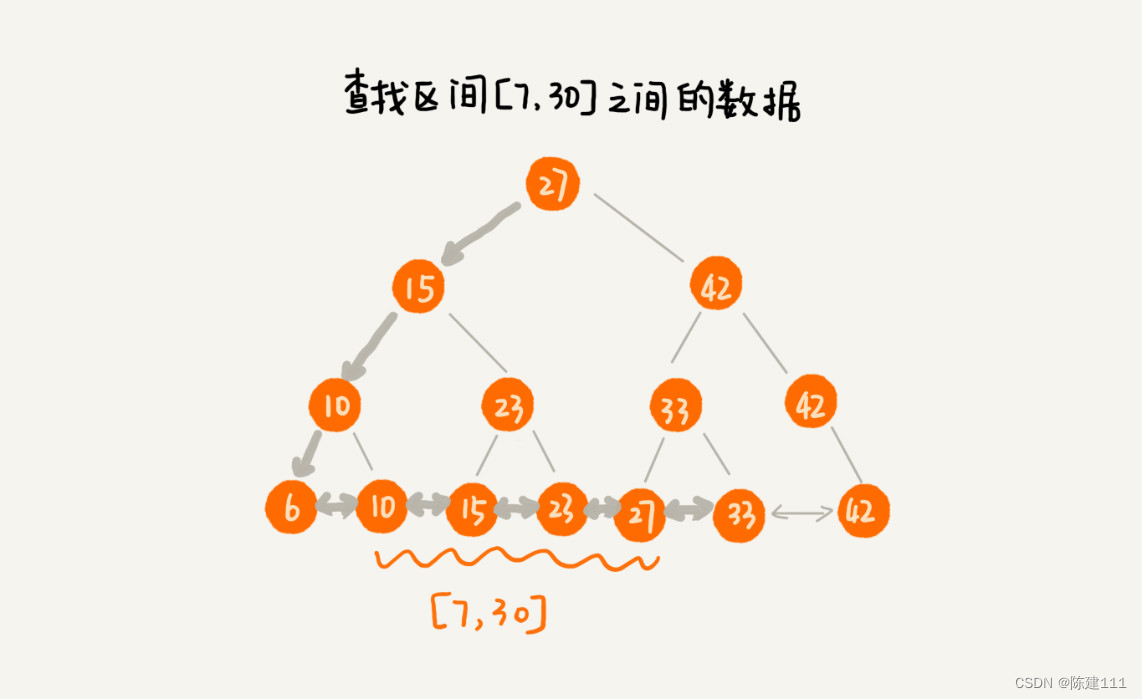
但是,我們要為幾千萬、上億的數據構建索引,如果將索引存儲在內存中,盡管內存訪問的速度非常快,查詢的效率非常高,但是,占用的內存會非常多。
比如,我們給一億個數據構建二級索引,那索引中會保護大約 1 億個節點,每個節點假設占 16 個字節,那就需要大約 1GB 的內存空間。給一張表建立索引,我們需要 1GB 的內存空間。如果我們要給 10 張表構建索引,那對內存的需求是無法滿足的。如何解決索引占用太多內存這個問題呢?
我們可以借助時間換空間的思路,把索引存儲到磁盤中,而非內存中。我們都知道,硬盤是一個非常慢速的存儲設備。通常內存的訪問速度是納秒級的,而磁盤的訪問速度是毫秒級別的。讀取同樣大小的數據,從磁盤總讀取花費的時間,是從內存中讀取所花費時間的上萬倍,甚至幾十萬倍。
這種將索引存儲在磁盤中的方案,盡管減少了內存消耗,但是在查找數據的過程中,需要讀取磁盤中的索引,因此數據查詢效率就相應降低很多。
二叉查找樹經過改造之后,支持區間查找的功能實現了。不過,為了節省內存,如果把樹存儲在硬盤中,那么每個節點的讀取(或者訪問),都對應一次磁盤 IO 操作。樹的高度就等于每次查詢數據時磁盤 IO 操作的次數。
前面說過,比起內存讀寫操作,磁盤 IO 操作非常耗時,所以我們優化的重點就是盡量減少磁盤 IO 的次數,也就是盡量降低樹的高度。那如何降低樹的高度呢?
我們來看下,如果我們把索引構建成 m 叉樹,高度是不是比二叉樹要小呢?如圖所示,給 16 個數據構建二叉樹索引,樹的高度是 4,查找一個數據,需要 4 個磁盤 IO 操作(如果根節點存儲子內存中,其他節點存儲在磁盤中),如果對 16 個數據構建五叉樹索引,那高度只有 2,查找一個數據,對應只需要 2 次磁盤操作。如果 m 叉樹中的 m 是 100,那對一億個數據構建索引,樹的高度也只是 3,最多只要 3 次磁盤 IO 就能獲取到數據。磁盤 IO 變少了,查找數據的效率也就提高了。


如果我們將 m 叉樹實現 B+ 樹索引,用代碼實現出來,就是下面這樣剛子(假設我們給 int 類型的數據庫字段添加索引,所以代碼中的 keywords 是 int 類型的)。
/*** 這是B+樹非葉子節點的定義** 假設keywords=[3, 5, 8, 10]* 4個鍵值將數據分為5個區間:(-INF,3), [3,5), [5,8), [8,10), [10,INF)* 5個區間分別對應: children[0]...children[4]** m值是事先計算得到的,計算的依據是讓所有信息的大小正好等于頁的大小:* PAGE_SIZE = (m-1)*4[keywords大小] + m*8[children大小]*/
public class BPlusTreeNode {public static int m = 5; // 5叉樹public int[] keywords = new int[m-1]; // 鍵值,用來劃分數據區間public BPlusTreeNode[] children = new BPlusTreeNode[m]; // 保存子節點指針
}/*** 這是B+樹的葉子節點的定義。** B+樹中的葉子節點跟內部節點是不一樣的* 葉子節點存儲的是值,而非區間。* 這個定義里,每個葉子節點存儲3個數據行的鍵值及地址信息。** k是事先計算得到的,計算的基于是讓所有信息的大小正好等于頁的大小* PAGE_SIZE = k*4[keywords大小] + k*8[dataAddress大小]+8[prev大小]+8[next大小]*/
public class BPlusTreeLeafNode {public static int k = 3;public int[] keywords = new int[k]; // 數據的鍵值public long[] dataAddress = new long[k]; // 數據地址public BPlusTreeLeafNode prev; // 這個節點在鏈表中的前驅節點public BPlusTreeLeafNode next; // 這個節點在鏈表中的后繼節點
}
我稍微解釋下這段代碼。
對于相同個數的數據構建 m 叉索引,m 叉樹中的 m 越大,那樹的高度就越小,那 m 叉樹中的 m 是不是越大就越好呢?到底多大才最合適呢?
不管是內存中的數據,還是磁盤中的數據,操作系統都是按頁(一頁大小通常是 4KB,這個值可以通過 getconfig PAGE_SIZE 命令查看)來讀取,一次會讀一頁的數據。如果讀取的數據量超過一頁的大小,就會觸發多次 IO 操作。所以,我們在選擇 m 大小的時候,要盡量讓每個節點大小等于一個頁的大小。讀取一個節點,只需要一次磁盤 IO 操作。
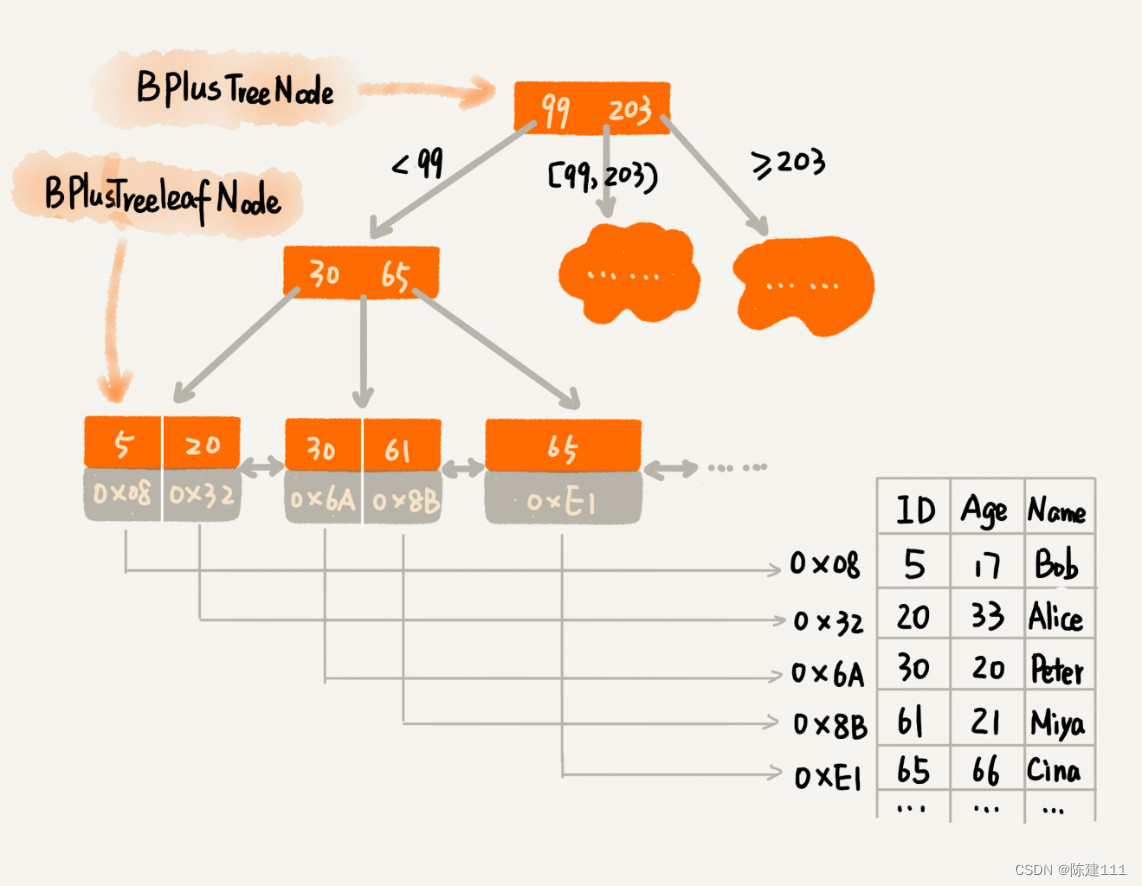
正式因為要時刻保證 B+ 樹索引是一個 m 叉樹,所以,索引的存在會導致數據寫入的速度降低。實際上,不光寫入數據會變慢,刪除數據也會變慢。這是為什么呢?
我們在刪除某個數據時,也要對應的更新索引節點。這個處理思路有點類似跳表中刪除數據的處理思路。頻繁的數據刪除,就會導致某個子節點中,子節點的個數變得非常少,長此以往,如果每個節點的子節點都比較少,勢必會影響索引的效率。
我們可以設置一個閾值。在 B+ 樹中,閾值等于 m/2。如果某個節點的子節點個數小于 m/2,我們就將他跟相鄰的兄弟節點合并。不過,合并之后的節點個數有可能超過 m。針對這種情況,我們可以借助插入數據時候的處理方法,再分裂節點。
文字描述不是很直觀,我舉了一個刪除操作的例子,你對比看下(圖中的 B+ 樹是一個五叉樹。我們限定葉子節點中,數據的個數少于 2 個就合并節點;非葉子節點中,子節點的個數少于 3 個就合并節點)。
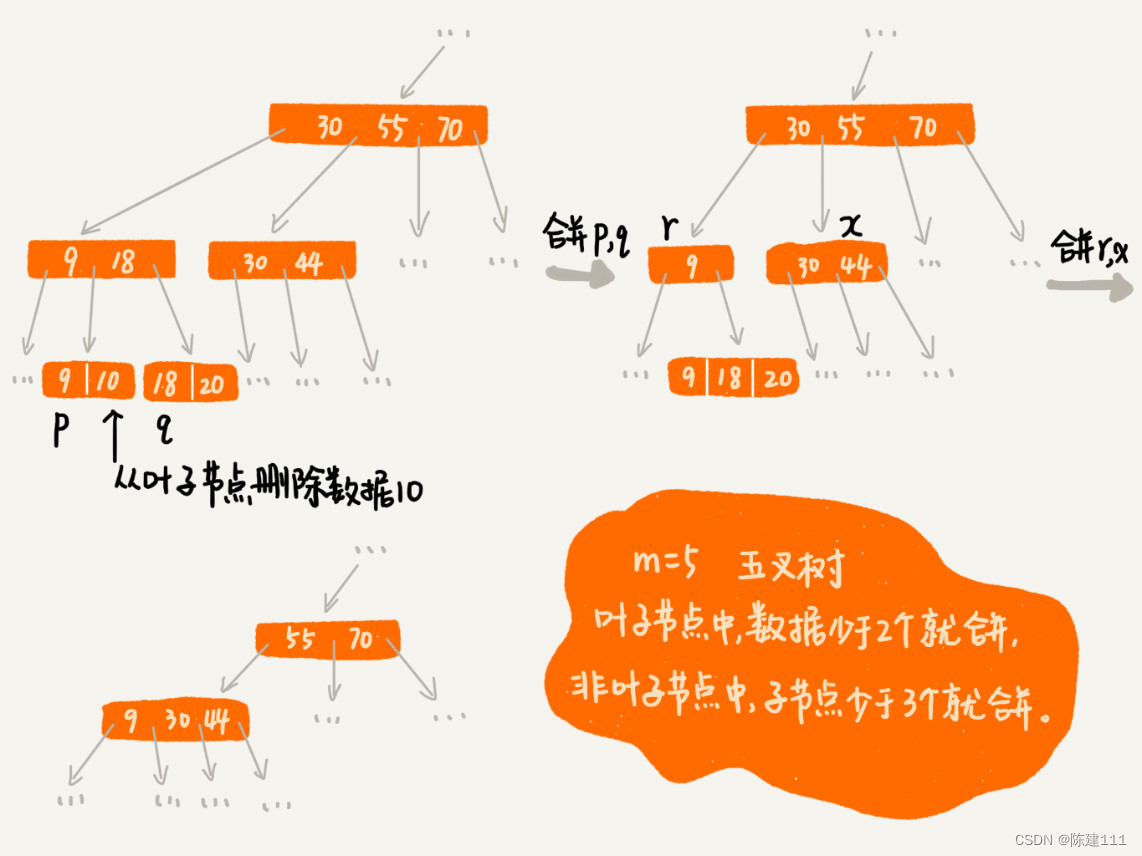
數據庫索引以及 B+ 樹的由來,至此就講完了。你有沒有發現,B+ 樹的結構和操作,跟跳表非常類似。理論上將,對跳表稍加改造,也可以替換 B+ 樹,作為數據的索引實現。
B+ 樹發明與 1972 年,跳表發明與 1989 年,我們可以大膽猜想下,跳表的作者可能就是受到了 B+ 樹的啟發,才發明出跳表來的。不過,這個也無從考證了。
總結
本章,講解了數據庫索引的實現,依賴的底層數據結構,B+ 樹。它通過存儲在磁盤的多叉樹結構,做到了時間、空間的平衡,既保證了執行效率,又節省了內存。
前面的講解中,為一步一步詳細地給你介紹 B+ 樹的由來,內容看起來比較零散。為了方便你掌握和記憶,這里再總結一下 B+ 樹的特點:
- 每個葉子節點中子節點的個數不能超過 m,也不能小于 m/2。
- 根節點的子節點個數可以不超過 m/2,這是一個例外。
- m 叉樹只存儲索引,并不真正存儲數據,這個有點而類似跳表。
- 通過鏈表將葉子節點串聯在一起,這樣可以方便按區間查找。
- 一般情況,根節點會被存儲在內存中,其他節點存儲在磁盤中。
除了 B+ 樹,你可能還聽說過 B 樹、B- 樹,這里簡單提一下。實際上 B- 樹就是 B 樹,英文翻譯為 B-Tree,這里的 “-” 并不是相對 B+ 樹中的 “+”,而只是一個連接符。這個很容易誤解,所以我強調下。
而 B 樹實際上是低級版的 B+ 樹,或者說 B+ 樹是 B 樹的改進版。B 樹跟 B+ 樹的不同點主要集中在這幾個地方:
- B+ 樹中的節點不存儲數據,只存儲索引,而 B 樹中的節點存儲數據;
- B 樹中的葉子節點并不需要鏈表來串聯。
也就是說,B 樹只是一個每個葉子節點個數不能小于 m/2 的 m 叉樹。




)
】ControlNet 和 IP-Adapter 之間的區別有哪些?)


進程間通信IPC)
:數據傾斜優化)









