在程序開發中，算法是解決問題的核心。本篇博客將詳細講解一種高效的查找算法——二分查找，并通過Java代碼示例幫助你理解其實現和應用。
如果你覺得這篇文章對你有幫助，不要忘記點贊、收藏和關注我，這將是對我最大的支持和鼓勵！
什么是算法？
算法是解決問題的一系列步驟或規則。它們是計算機程序的核心，決定了程序的性能和效率。一個好的算法可以極大地提高程序的運行速度和資源利用率。
大O表示法
大O表示法用于描述算法的效率，特別是它在數據規模增長時的表現。常見的大O表示法包括：
- O(1)：常數時間，不論數據規模多大，執行時間都不變。
- O(log n)：對數時間，常見于二分查找。
- O(n)：線性時間，算法的執行時間與數據規模成正比。
- O(n log n)：線性對數時間，常見于快速排序、歸并排序等。
- O(n^2)：平方時間，常見于簡單排序算法，如冒泡排序。
- O(2^n)：指數時間，常見于解決復雜問題的遞歸算法。
二分查找簡介
二分查找是一種用于在有序數組中查找特定元素的高效算法。其基本思想是通過逐步縮小查找范圍，將查找時間復雜度降低到 O(log n)。相比于線性查找的 O(n)，二分查找的效率要高得多。
二分查找步驟
- 找到數組的中間元素。
- 如果中間元素正好是目標元素，查找成功。
- 如果目標元素比中間元素小，則在左半部分繼續查找。
- 如果目標元素比中間元素大，則在右半部分繼續查找。
- 重復上述步驟，直到找到目標元素或范圍縮小為零。
二分查找圖解
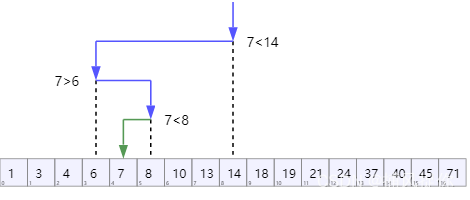
Java實現
下面是一個簡單的Java代碼實現：
public class BinarySearch {public static int binarySearch(int[] array, int target) {int low = 0;int high = array.length - 1;while (low <= high) {int mid = (low + high) / 2;int guess = array[mid];if (guess == target) {return mid;} else if (guess > target) {high = mid - 1;} else {low = mid + 1;}}return -1; // 表示未找到}public static void main(String[] args) {int[] array = {1, 3, 5, 7, 9};int target = 7;int result = binarySearch(array, target);System.out.println("元素 " + target + " 的索引為: " + result);}
}
代碼解釋
binarySearch方法接受一個有序數組和一個目標值作為輸入。- 通過初始化
low和high指針，逐步縮小查找范圍。 - 計算中間位置
mid并檢查其值是否等于目標值。 - 根據目標值與中間值的比較結果，調整
low和high指針。 - 循環直到找到目標值或范圍縮小為零。
算法分析
- 時間復雜度：二分查找的時間復雜度為 O(log n)，因為每次查找都會將查找范圍減半。
- 空間復雜度：二分查找的空間復雜度為 O(1)，因為它只使用了常數的額外空間。
示例運行結果
運行上述代碼，你將看到以下輸出：
元素 7 的索引為: 3
練習題
- 修改
binarySearch方法，使其能處理包含重復元素的數組，并返回第一個匹配的元素。 - 實現一個線性查找算法，并比較它與二分查找的性能。
總結
通過本文的學習，我們了解了二分查找的基本概念、實現步驟和Java代碼示例。二分查找是一種高效的查找算法，適用于大多數有序數據集的查找問題。
如果你覺得這篇文章對你有幫助，請點贊、收藏，并關注我的CSDN博客。我會持續分享更多高質量的算法和編程知識。
感謝你的閱讀和支持！如果有任何問題或建議，歡迎在評論區留言，我會盡快回復。
希望這篇博客對你有幫助。如果有任何問題或需要進一步的解釋，請告訴我！
