---

期刊: IEEE Trans. Vis. Comput. Graph.（發表日期: 2019）
作者: Johanna Schmidt; Dominik Fleischmann; Bernhard Preim; Norbert Br?ndle; Gabriel Mistelbauer

摘要

時間數據可視化用于分析隨時間變化的因變量，其中時間是一個獨立變量。由于需要向用戶傳達許多方面的信息（例如，時間和變量的變化），可視化時間數據本質上是困難的。這是可視化中的一個重要主題，已經設計了許多處理不同任務的可視化技術。在本文中，我們提出了一種新穎的概念——彈出圖（popup-plots），其中利用常見的3D旋轉交互來瀏覽數據。這使用戶能夠從不同的角度查看數據，而無需學習和適應新的交互概念。因此，彈出圖是一種新穎的可視化和與時間相關的因變量交互方法。我們通過根據時間彎曲空間來擴展2D圖來加入時間信息。彎曲是基于球坐標系方法計算的，其受到朝向圖的視角的持續影響。因此，可以從不同的角度觀察圖，之間無縫切換，提供了分析所表示數據不同方面的可能性。由于當前視角是通過數據的形狀來表示的，用戶可以推斷出當前查看的數據的哪一部分。時間信息被編碼到可視化本身中，類似于樹的年輪。我們通過將其應用于來自兩個不同領域的數據（包括隨時間的空間位置上的測量），以及評估我們解決方案的可用性來演示我們的方法。

關鍵詞：時態數據、時間相關可視化、3D 繪圖、橢球坐標系。

1 引言

時空數據集的可視化本質上是一項具有挑戰性的任務[1]，因為必須以視覺方式傳達時間背景、隨時間的變化以及因變量之間的關系。因此，時間相關數據可視化 [2] 是一個新興主題，應用于許多不同領域。

在許多情況下，時間數據集由在連續時間點獲取的測量值組成。此類測量值可以是溫度 [3]、交通量 [4]、醫療參數 [5] 或可能隨時間變化的其他測量值。我們將此類測量稱為屬性。為了保持一致性，并且為了能夠比較隨時間變化的值，測量結果經常記錄在固定的空間位置。我們將這些位置稱為地標。作為此類數據集的一個示例，我們可以想象一份溫度值記錄，該記錄是在一個月內每天使用固定溫度計在特定空間位置測量的。地標、屬性和時間的組合類似于 3D 數據集，包含兩個因變量（屬性和地標）和自變量時間。不同的時間點可以定義為時間戳。

已經提出了幾種可視化技術來直觀地分析這種特定類型的數據。傳統的二維圖是一種廣泛使用且眾所周知的視覺表示形式，可用于可視化地標位置處的屬性。可以通過投影來包含時間信息（例如，使用顏色或線寬）。另一種方法是將二維表示擴展到三維以顯示時間。在這種情況下，三個數據維度被映射到三個空間維度。在這種情況下，最簡單的表示是 3D 曲面圖，將屬性值隨時間變化連接起來。三維時間數據的另一個突出且廣泛采用的視覺表示是時空立方體 [6]。最初，它使用二維來顯示二維空間信息（例如地圖數據），使用第三維來可視化時間；基本上沿著時間軸級聯幾個二維圖[7]。時空立方體的概念還可用于顯示隨時間變化的地標處的屬性，其中每個數據維度由三個空間維度之一編碼。

旋轉、縮放和平移等交互是探索三維數據的重要概念。我們利用它們，并在此提出了一種用于分析 3D 數據的 2.5D 圖的新概念，其中時間是交互的問題。從傳統且眾所周知的 2D 繪圖開始，通過使用 3D 旋轉改變觀察方向，相繼顯示更多時間信息。這是通過使用橢球模型而不是笛卡爾坐標系來實現的。與現有技術相比，橢圓體模型允許彎曲空間以查看時間。這種彎曲直接受到觀看方向的影響，而觀看方向由用戶控制。我們將這種新的可視化技術稱為彈出圖（PP），其靈感來自于著名的彈出賀卡。如果這樣的卡片關閉，它是平坦的（不顯示時間），但是當打開時，連續更多的結構（時間）變得可見。

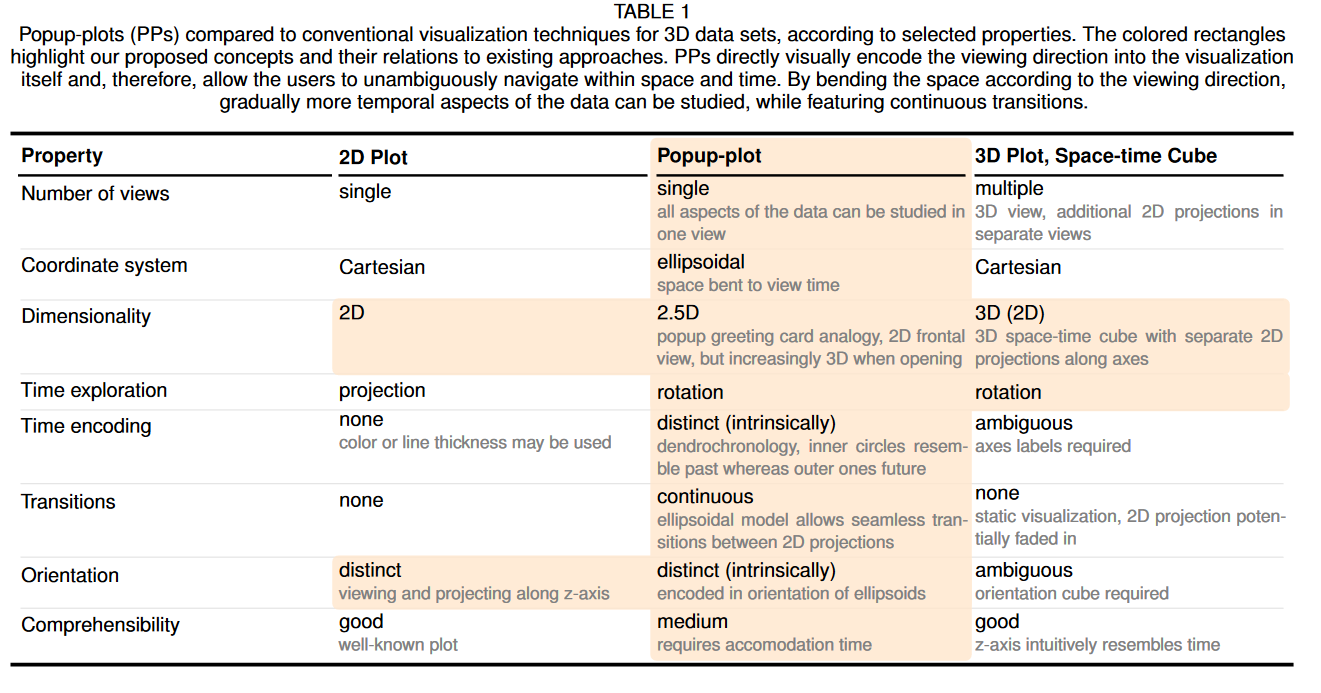
彈出圖（PP）使我們能夠將各個方面固有地編碼到可視化中，并通過簡單地改變觀察方向來研究數據的不同方面。因此，PP 允許在一個視圖中檢查數據，而無需使用投影、多個視圖或刷動和鏈接。由于空間彎曲，可以通過查看可視化的形狀來推斷數據的當前查看方向。橢球模型在視覺上對時間信息進行編碼，類似于樹的年輪，其中內環類似于過去。此外，解析橢球模型提供了不同觀察方向之間的無縫過渡。表 1 概述了傳統可視化技術與我們提出的 PP 之間的差異。

我們在第 2 節中概述了相關的最先進技術。第 3 節中描述的彈出圖 (PP) 的新穎概念已作為基于 Web 的應用程序實現（參見第 4 節） 。為了證明彈出圖（PP）的多功能性，我們將它們應用于兩個數據集，一個來自醫學，另一個來自流量分析（參見第 5 節）。這項工作在第 6 節中進行評估，并在第 7 節中進行討論。我們在第 8 節中對未來的方面進行總結。

2 相關工作

為了涵蓋我們工作的所有方面，我們必須參考有關可視化的幾個領域。最突出的是時間數據可視化和時空數據可視化，其次是交互技術。由于我們的用例基于醫療數據和交通數據，因此我們隨后對這些學科中的數據可視化方法進行回顧。

時態數據可視化描述了允許分析時態數據集的可視化系統和技術。現有的時態數據可視化應用程序非常異構，因為它們是為了解決不同領域內的各種任務而開發的。 Aigner 等人對時態數據可視化進行了全面的調查。 [2]。許多技術使用線性隱喻（即時間線）將時間可視化為連續變量。例如，ThemeRiver（Havre 等人[8]）和堆疊圖（Byron 和 Wattenberg [9]）沿水平時間軸繪制屬性值。此類應用程序對于探索屬性隨時間的變化以及研究單個時間戳內屬性的關系非常有用。這同樣適用于沿線性時間軸以成對方式連接相關信息的弧線圖[10]。循環圖采用時間的水平表示來描繪單變量 [11] 和多變量 [12] 時間序列數據中的循環模式。托明斯基等人。 [13]使用線性表示在時間輪中顯示時間，但建議圍繞時間軸以圓形布局排列屬性。托明斯基等人。 [14]后來將該技術擴展到三個維度。

其他方法也使用第三維來編碼可視化中的附加信息。 Timetunnel，由 Akaishi 和 Okada [15] 提出，以 3D 扇形方式圍繞中央時間條定位 2D 繪圖。流可視化中的隱喻可用于顯示屬性隨時間的變化 [16]，傳達故事情節的演變 [17]，或將屬性解釋為 3D 對象 [18] 以顯示其時間進程。更復雜的結構（例如 Noirhomme-Fraiture [19] 的變焦星）可用于包含附加信息（例如直方圖），以便對數據進行更詳細的分析。

由于線性時間軸在較大數據集的情況下可能會消耗大量空間，因此已經研究了徑向布局以有效地傳達時間信息空間。通過使用顏色[20]或分層方法[21]，可以觀察屬性隨時間的變化。韋伯等人。 [22]提出了一個圖，其中屬性沿著顯示時間進程的螺旋可視化。最近的方法采用更復雜的幾何變換來顯示時間信息。巴赫等人。 [23]使用基于曲線的布局來表示可視化中的時間。其他作者利用平行坐標并找到了通過合并時間信息來增強繪圖的新方法。格倫德爾等人。 [24]提出了一個小部件來探索并行坐標圖中的時間并比較兩個連續軸之間的時間關系。約翰遜等人。 [25]使用深度線索來整合平行坐標中的時間。通過這種方式，可視化可以在關注屬性時揭示數據中的時間模式。

我們使用新穎的曲線布局來顯示時間，這取決于觀察方向，這意味著球形或橢球體模型。這不僅提供了以與傳統和廣泛采用的繪圖相同的方式探索數據的可能性，而且還提供了通過改變觀看方向或更一般地通過交互來探索時間。此外，不同數據視圖之間的無縫轉換可以評估一個視圖內的時空關系。我們的方法類似于由Zhao等人提出的環圖。 [26]，將時間編碼為環。通過顯示與 2D 視圖交織在一起的 3D 視圖，可以探索數據中的模式。然而，環圖不會根據視角而改變，因此時空仍然是平坦的。

由于時間數據通常與空間位置相關，因此這兩個術語的組合導致時空數據的可視化[27]。我們提出的可視化技術也可以應用于一維時空數據集[28]。然后，第一因變量表示空間（例如，沿路徑的一維位置），第二因變量定義在這些空間位置測量的屬性。時空立方體是可視化此類數據的直觀且廣泛的概念[29]。作者描述了沿每個軸投影和展平的方法以及提取和轉換操作。與我們提出的技術相關的操作是彎曲和展開。

與我們的概念的主要區別在于，時空立方體考慮平坦時空，空間和時間之間具有不連續的過渡。然而，在時空數據的配置中[30]，例如，當將地理地圖作為兩個依賴屬性時，我們的方法將不會類似于令人滿意的視覺表示。因此，我們的方法不適用于完整分析這些數據。

交互技術支持對時空數據的理解。處理多維數據的典型方法是在多個視圖中呈現數據的不同方面[31]。我們專門設計了我們的方法，使用戶可以在一個視圖中直接與三維圖進行交互，以研究數據的不同方面。這是通過隱含時空橢球模型來實現的。空間折疊已經被其他方法所應用。埃爾姆奎斯特等人。 [32]提出了一種折疊空間以在探索過程中保留上下文和概覽的技術。當空間彎曲將二維地圖延伸到三維時，人們會得到折疊空間范圍的印象以及兩點之間距離的概念。同樣，我們對空間進行變形，以實現不同觀看視角之間的無縫過渡。 van Wijk 和 Nuij [33] 描述了對地圖上兩點之間的行進距離進行編碼的另一種方法。他們在過渡過程中使用了距離與相機速度和高度的非線性映射。

由于我們的 PP 根據觀察方向延伸到三維，我們還對數據點應用非線性（橢圓體）映射，以實現平滑和無縫的過渡。與 Azuma 等人類似。 [34]我們建議根據需要更改可視化的表示，但在我們的例子中取決于當前的觀看方向。科尼哈等人。 [35]介紹了一種在多視圖環境中研究曲線族的方法。對屬性隨時間的時間進展的分析也可以解釋為研究一組曲線。我們提出的方法允許通過 3D 交互來研究屬性值。

醫療應用程序以不同的方式利用時間和時空數據可視化。醫學上的時間進展通常是指一名或多名患者的病史，以研究模式[36]或事件[37]。在這種情況下，事件帶有時間戳但離散，并且通常無法隨著時間的推移在特定地標處連續監控。因此，事件可視化并不直接適用于我們的時態數據類型。在其他情況下，時空可視化技術用于描述測量數據的時間變化。 De ? anBen 等人。 [38]使用多個視圖來顯示心血管動力學的時間進展。他們同時使用 2D 圖形和 3D 渲染圖像。曹等人。 [39]關注的是測量間隔并不總是在簡單的線圖中顯示的事實。格拉瑟等人。 [40]使用平行坐標向三維的擴展來表達縱向灌注磁共振研究中的時間。在他們的可視化中，可以清楚地識別描述腫瘤邊界局部異質性的峰值。我們的方法可用于研究在局部感興趣點進行的醫學測量的時間進展。

交通數據包含多種不同的可能數據類型，包括空間中移動的物體的采樣位置，以及匯總研究，例如沿特定路線的物體數量。收集這些數據用于統計評估或實時監控交通狀況[41]。時間是一個重要方面，因為交通狀況通常在一天或一年內變化很大。交通數據可視化的主要研究目標是通過提供合適的解決方案[28]（如交互、聚合和內存管理方法）來分析大量數據。還有其他方法專注于分析交通系統中特定路線沿線的參數。托明斯基等人。 [42]實現了時空墻，用于分析隨時間變化的軌跡的屬性。格羅特爾等人。 [43]采用不同可視化技術（即平行坐標和熱圖）的組合來分析軌跡。我們的方法可用于可視化沿著預定義軌跡（例如火車軌道或高速公路）的屬性的時間進程。

3 彈出圖

彈出圖 (PP) 描述了一種新穎的 2.5D 類型的圖，用于時態數據的可視化。我們使用 3D 橢球模型來代替笛卡爾坐標系來顯示數據，這在 3.1 節中有詳細解釋。 PP 通過根據當前觀察方向連續添加時間信息來擴展傳統的 2D 繪圖。 PP 的概念允許我們在單一視圖中查看數據并與之交互。

PP 可應用于由三個數據維度組成或可投影到三個數據維度的數據，其中一維類似于時間。在本文中，我們處理的 3D 數據集由由兩個因變量（屬性、地標）和一個自變量（表示時間戳）定義的數據點組成。橢球模型為每個數據點分配一個 3D 位置。因此，PP 提供了一種在 3D 空間中繪制數據點的新穎概念，其中 3D 旋轉用作交互機制，從不同角度研究數據。現有的可視化技術也適用于點圖和線圖，可以用于增強視覺表示（例如，通過添加 viewcube [44]）。由于 PP 的橢球模型主要描述數據點如何變換，因此它不限于任何特定的可視化技術或應用領域。 3.2 節概述了數據的視覺表示和交互概念。

3.1 橢球模型

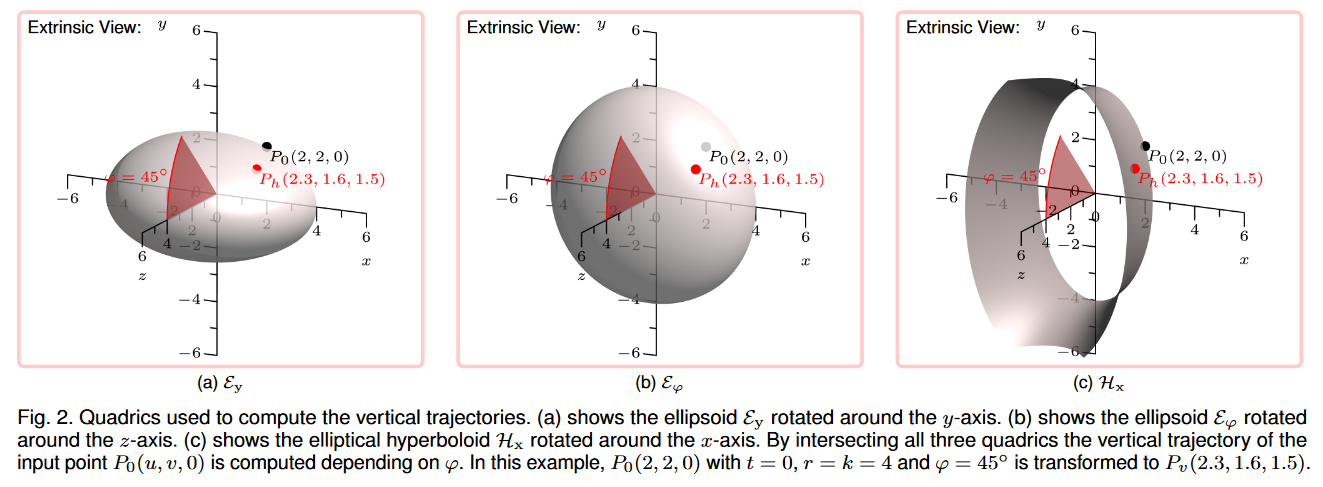
PP 采用橢圓體模型將數據點映射到 3D 位置。隨后，我們解釋了數學背景并介紹了該模型的理論概念。我們用二次曲面來模擬時空，例如橢球體和雙曲面。在本節中，我們使用球坐標表示法，其中幾何點由三元組 (r, θ, φ) 描述。我們進一步提出 PP 的內在和外在觀點。內在視圖顯示從用戶角度使用 PP 可視化的數據，從而產生一個橢圓彎曲的坐標系，其原點從笛卡爾 xy 平面連續向外移動。相反，外部視圖從固定的觀察者角度展示了嵌入笛卡爾坐標系的轉換后的數據。應該注意的是，所有附圖都是通過在矢量圖形語言 Asymptote 中實現并程來實現的 [45]。

PP 中的主要交互概念是 3D 旋轉。因此，為用戶提供了兩個自由度 θ 和 φ，分別類似于從左到右和從上到下的視角。不同的視角設置將導致數據以不同的方式可視化。同一數據點的所有可能的 3D 位置都被匯總為軌跡。水平觀察方向由 θ 控制，改變 θ 時生成的數據點的 3D 位置集合稱為水平軌跡（參見第 3.1.1 節）。類似地，φ 引導從上到下的觀察方向，因此我們將改變 φ 時生成的一組數據點 3D 位置稱為垂直軌跡（參見第 3.1.2 節）。最初，數據點的軌跡是針對兩個視角分別確定的，但隨后組合成單個連續軌跡（參見第 3.1.3 節）。由于時間是沿著朝向觀察者的正 z 軸編碼的，因此我們只考慮正半空間并使用 xy 平面剪切所有二次曲面。

3.1.1 水平軌跡

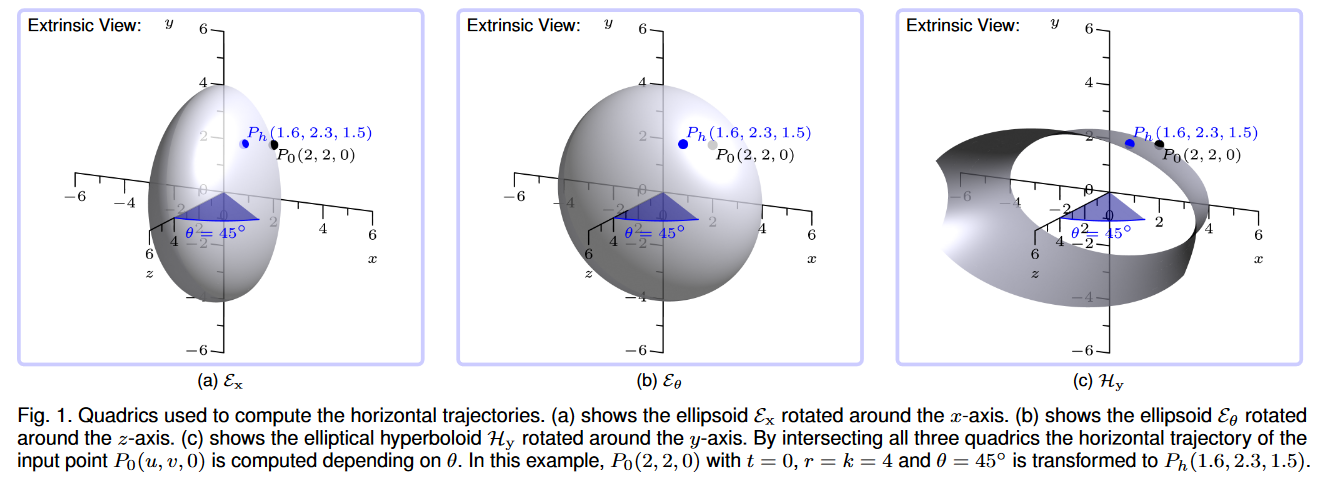
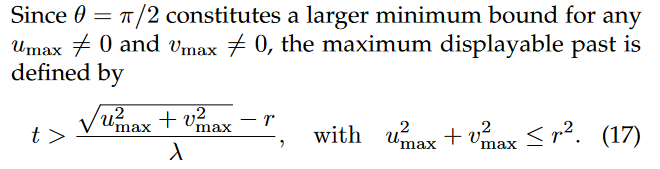
3.1.2 垂直軌跡

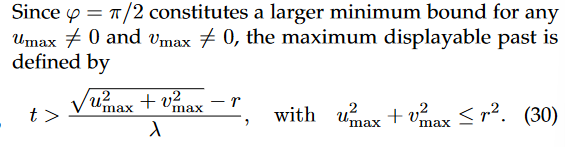
3.1.3 組合軌跡

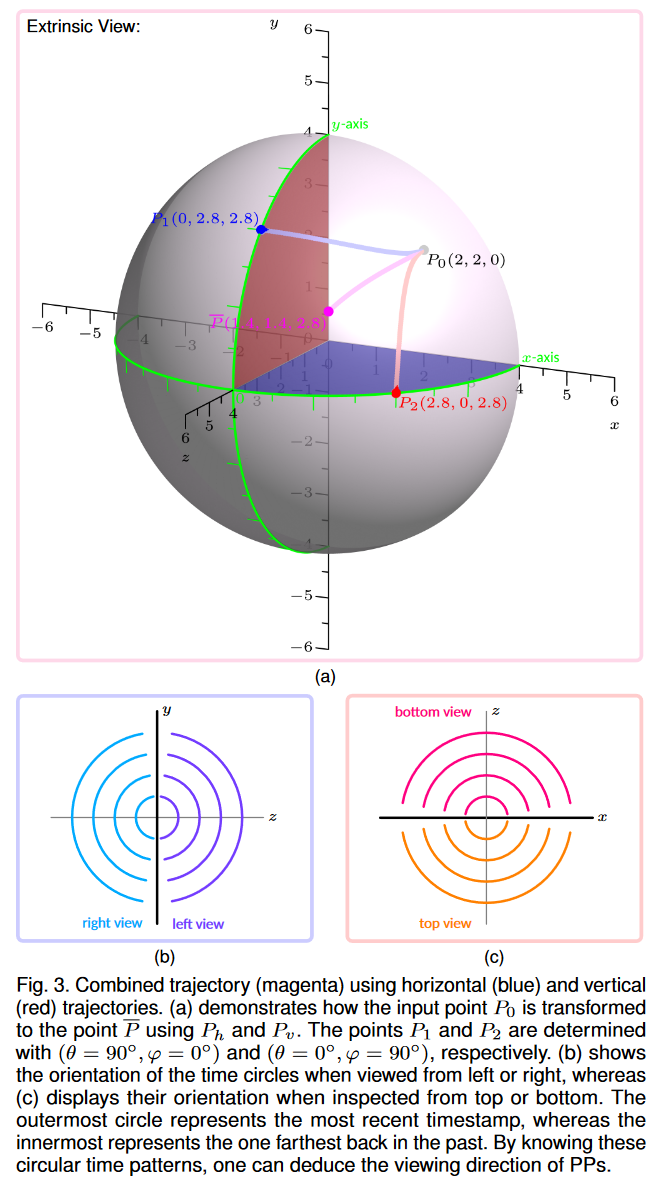
3.2 視覺映射與交互

橢球模型根據觀察方向定義 3D 數據點的位置。該模型確保不同觀看視角之間的連續無縫過渡。因此，PP 提供了一個在三個維度上顯示數據的基本框架，然后可以通過采用現有的可視化技術來豐富該框架。以最簡單的形式，我們建議在可視化中將數據點呈現為球體。我們進一步建議將同一時間的轉換數據點連接到連接曲線，例如，通過使用 Catmull-Rom 樣條線。隨后，對這些樣條線進行等距采樣，并將獲得的位置用于渲染。圖 4 概述了這些提出的視覺映射策略。

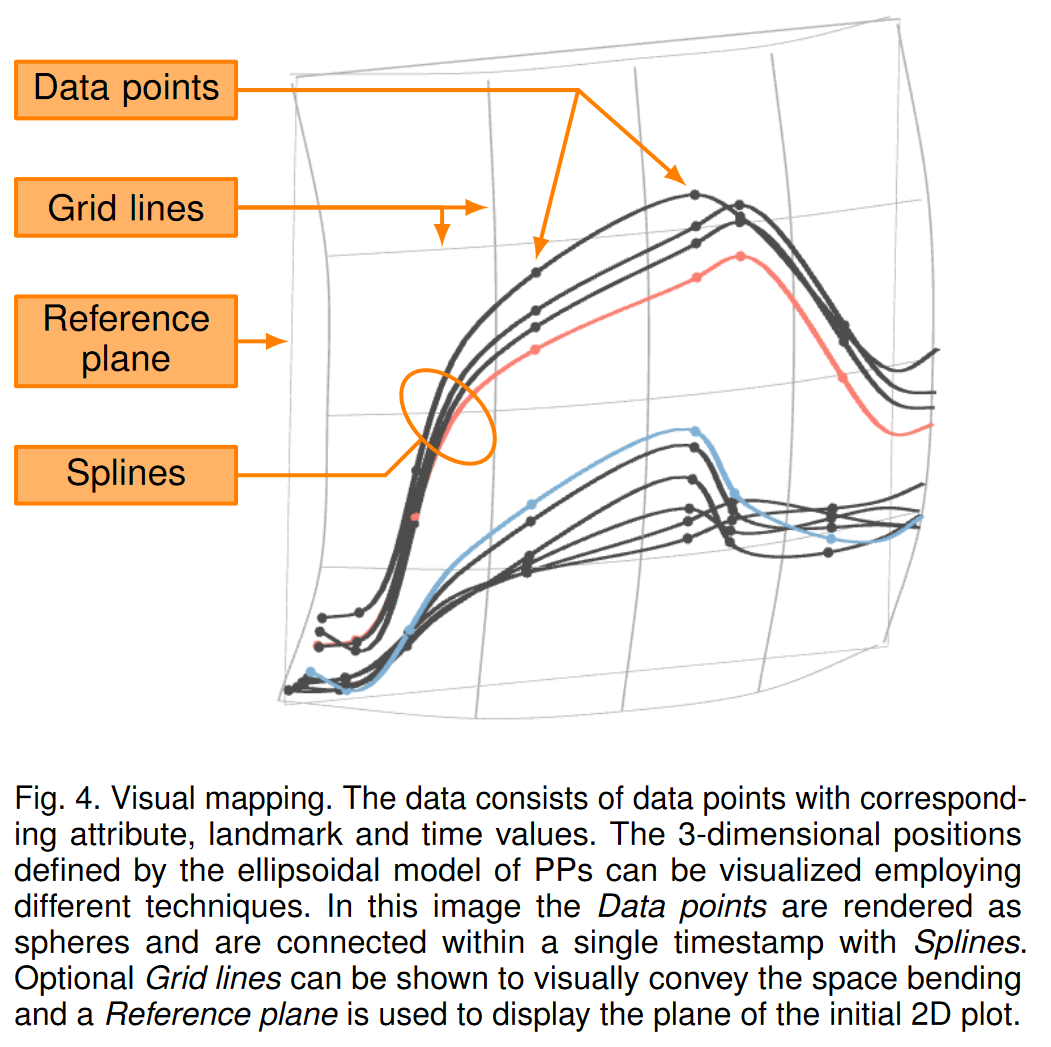
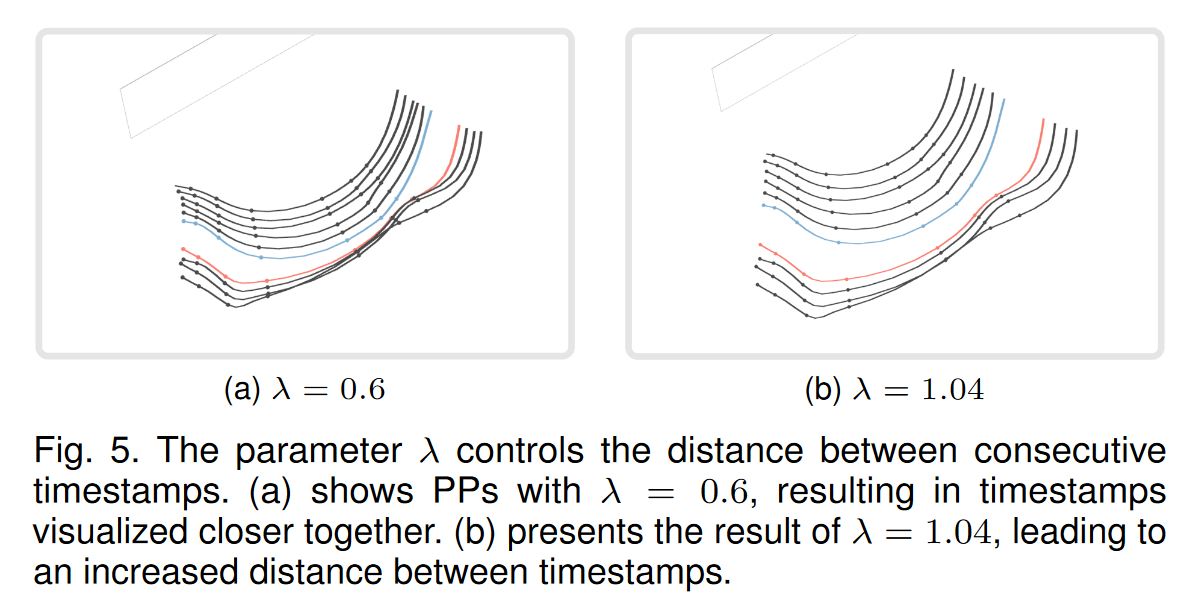
PP 可視化會受到參數 λ 和 r 的影響。時間戳之間的距離由 λ 控制（見圖 5），允許用戶放大和縮小 PP。不同的 λ 設置也使得 PP 能夠適應各種類型的數據集，甚至是不同時間跨度的數據集。橢圓體模型的半徑 r 定義了繪圖的大小和可顯示時間戳的數量（即最大可顯示過去，請參見公式 17 和公式 30）。

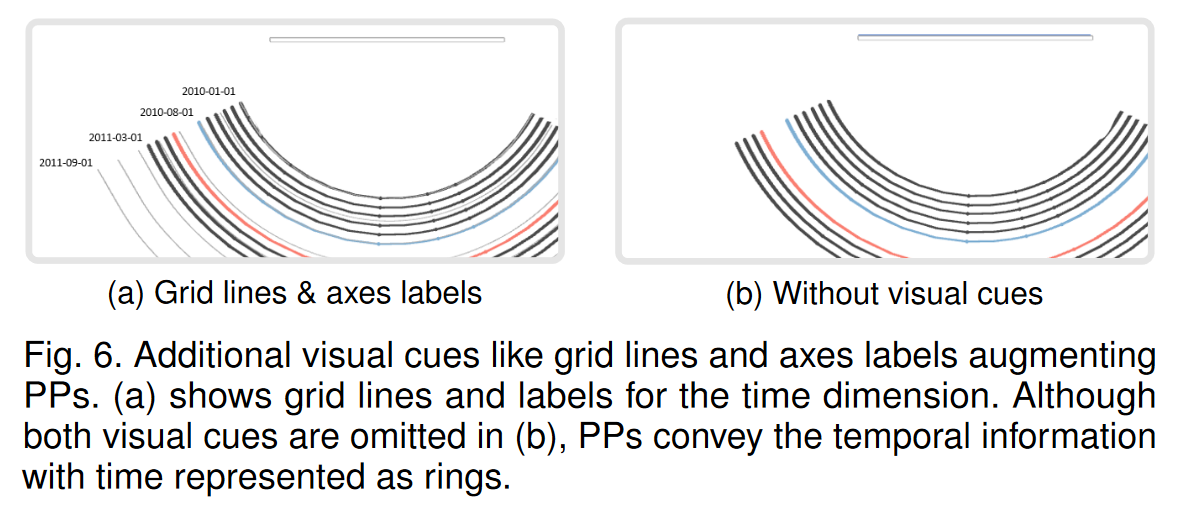
除了旋轉之外，我們還測試了進一步交互的可能性來分析數據。可以在可視化中顯示網格線和標簽（參見圖 4），以更好地傳達上下文信息。網格線的形狀和位置也是根據PP模型計算的。由于當前的觀看方向定義了可視化的形狀，因此，還可以在不閱讀標簽或解釋網格線的情況下解釋 PP（參見圖 6）。相反，當使用時空立方體等傳統技術時，人們總是需要參考線索才能解釋可視化。我們還添加了通過單擊按鈕快速選擇預定義數據視角的可能性。這些視角之一是傳統的 2D 圖，由 θ = 0°、φ = 0° 定義。另外兩個視角是從頂部（θ = 0°，φ = 90°）和從側面（θ = 90°，φ = 0°）查看數據。 PP 不限于這些預定義的設置，其他預定義的視角可能有助于強調數據中的某些模式。我們還添加了通過單擊各自的 3D 樣條曲線來選擇各個時間戳的可能性。然后，所選時間戳的更多詳細信息（即日期和最小/最大屬性值）將顯示在單獨的窗口中。不同的時間戳可以通過其分配的類別顏色在視覺上區分。為了一般性，我們沒有包含任何進一步的類別語義。類別可以映射到數據中特定領域的語義組（例如，通過聚類識別）。

PP 方法涵蓋了時態數據可視化所需的許多方面（表 1 中介紹）：

觀看次數。 PP 只需要一個視圖即可傳達數據集的所有方面。數據的不同視圖并不代表在單獨窗口中顯示的封裝狀態，而是通過用戶直接與數據交互來實現。
坐標系。數據點的位置根據PP橢球模型計算。可以識別屬性值隨時間顯著變化的地標以及時間變化較小的地標。
維度。根據橢球模型，PP 采用 2.5D 數據表示。可以通過 3D 旋轉來實現對數據的進一步探索（其中還包含時間）。每次旋轉都會揭示數據的不同方面。
時間探索。從側面觀察（θ = 90 且 φ = 0）時，會顯示屬性的時間進程。可以看出隨著時間的推移，屬性值是否持續增加或減少。當從頂部查看 PP（θ = 0 和 φ = 90）時，會顯示時間戳的數量和距離。
時間編碼。時間戳根據樹木的年輪進行編碼，過去的時間點位于內部。這種時間的循環編碼可以非常快速地識別較舊和較新的時間戳。人們可以識別時間戳是否大部分是等距的，或者它們之間是否存在較大的間隙。循環時間編碼表現出固有的時間順序。
過渡。 PP允許用戶在3D空間中自由旋轉。在旋轉過程中，PP 橢球模型保證了變換后的數據點位置的連續轉變。與數據集交互時看不到跳躍效果。
方向。這解決了 PP 的一個非常重要的方面，因為數據集的當前方向始終直接由可視化本身反映。這允許立即探索數據，而無需任何額外的視覺提示（例如，方向立方體）。
可理解性。由于 PP 會彎曲空間以顯示時間，因此可能需要一個初始適應階段來理解該概念。盡管如此，PP 提供了探索和解釋數據的豐富可能性。

4 實施

PP 是使用 JavaScript 和 WebGL 進行渲染的基于 Web 的解決方案。 2D 數據集存儲為 JSON 格式的文本文件。我們使用 ThreeJS (v. r84) [46] 來渲染，并使用 JQuery (v. 3.2.0) [47] 來實現用戶界面元素。我們的方法在配備 Intel Core i7 2.90GHz 處理器、16 GB RAM 和 NVIDIA GeForce GTX 670M 顯卡的系統上進行了測試，并在 Windows 8.1 64 位上使用網絡瀏覽器 Firefox（v. 52.0.2）。數據集的加載只需幾毫秒，并且交互是實時運行的。對于我們提出的兩個用例，該應用程序消耗了大約 300 MB（參見圖 7 和圖 8）。

5 結果

這項工作是由來自不同領域的兩個用例推動的。兩個用例的數據結構都適用于我們對包含兩個因變量和自變量時間的 3D 數據集的定義。隨后，我們解釋了如何使用 PP 來探索這些數據。

第一個用例屬于醫療領域，與稱為主動脈夾層 (AD) 的血管疾病有關。通常，在健康的血管中，血液在單個流動通道內流動。在 AD 的情況下，會形成幾個其他流動通道，導致容器直徑和壓力增加。由于這些通道并不是為了承受高血壓而設計的，它們最終往往會破裂，這是一種致命的事件。血管直徑是預測此類事件的重要指標。因此，主動脈直徑（屬性）是在特定測量點（標志）處評估的。這些測量必須在多次患者檢查（時間戳）中重復進行，以監測患者的健康狀況[48]。在我們的用例中，檢查了接受手術治療以縮小主動脈直徑的患者的數據集。 3D 數據集由十個時間戳組成，這些時間戳是在七年的時間內采集的。主動脈直徑是在主動脈沿線的 11 個標志處測量的。使用兩個類別來識別手術干預之前（藍色）和之后（橙色）的時間戳（見圖 7）。

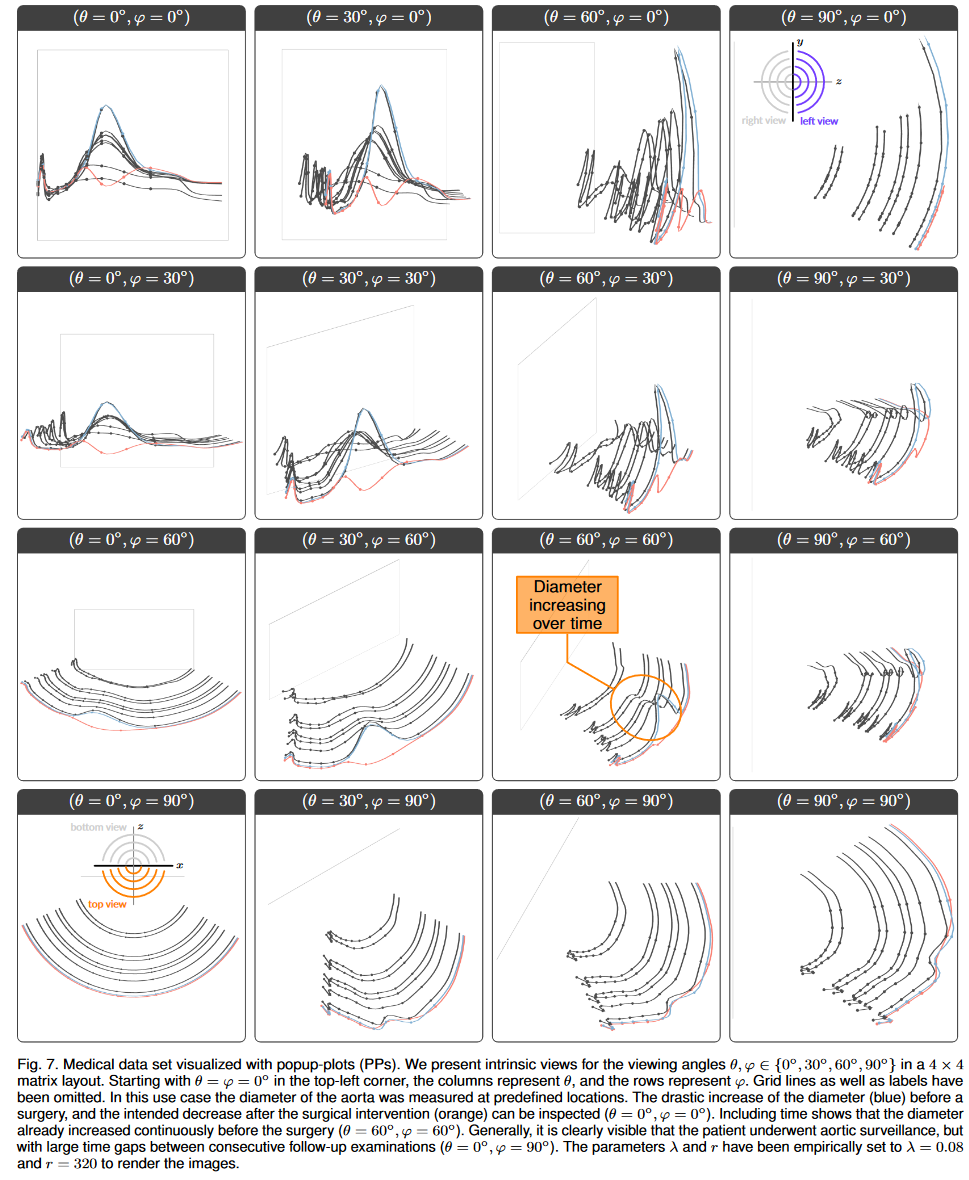
在中心標志處可以檢查相當不同的直徑值（θ = 0°，φ = 0°），而在外部標志處，直徑隨時間保持恒定。在手術干預之前可以看到最高直徑值（藍色）。當分析中包含時間時，我們可以認識到直徑的急劇增加是最近發生的（θ = 60°，φ = 60°，直徑隨著時間的推移而增加）。手術干預后立即對患者進行監測，由非常靠近的藍色和橙色時間戳表示。橙色時間戳還顯示了中間區域直徑的預期術后減小（θ = 30°，φ = 60°）。當查看時間戳（θ = 0°，φ = 90°）時，可以清楚地看到患者接受了定期醫療監測，但檢查之間的距離不同。由于中心區域的直徑值相當低，兩個時間戳描述的直徑值不同于數據集的其余部分。可以看出，這兩個時間戳描述了過去發生的檢查（θ = 30°，φ = 30°）。圖 7 中采用的矩陣視圖也可能包含在醫療報告中，以直觀地傳達時間和時間變化。

第二個用例與交通數據有關。在大城市的街道網絡中，有所謂的主動脈路線，它們對于整體交通狀況非常重要。這些路線可能是進出城市的高速公路或高速公路，或者繞開城市以引導周圍的交通。該用例的 3D 數據集包含沿著主動脈路線（穿過大城市的高速公路）行駛的車輛（汽車和卡車）數量。車輛數量（屬性）在計數站（地標）自動記錄。我們選擇了 24 個記錄，代表 2014 年一天的 24 小時（時間戳）。我們的 PP 結果如圖 8 所示。

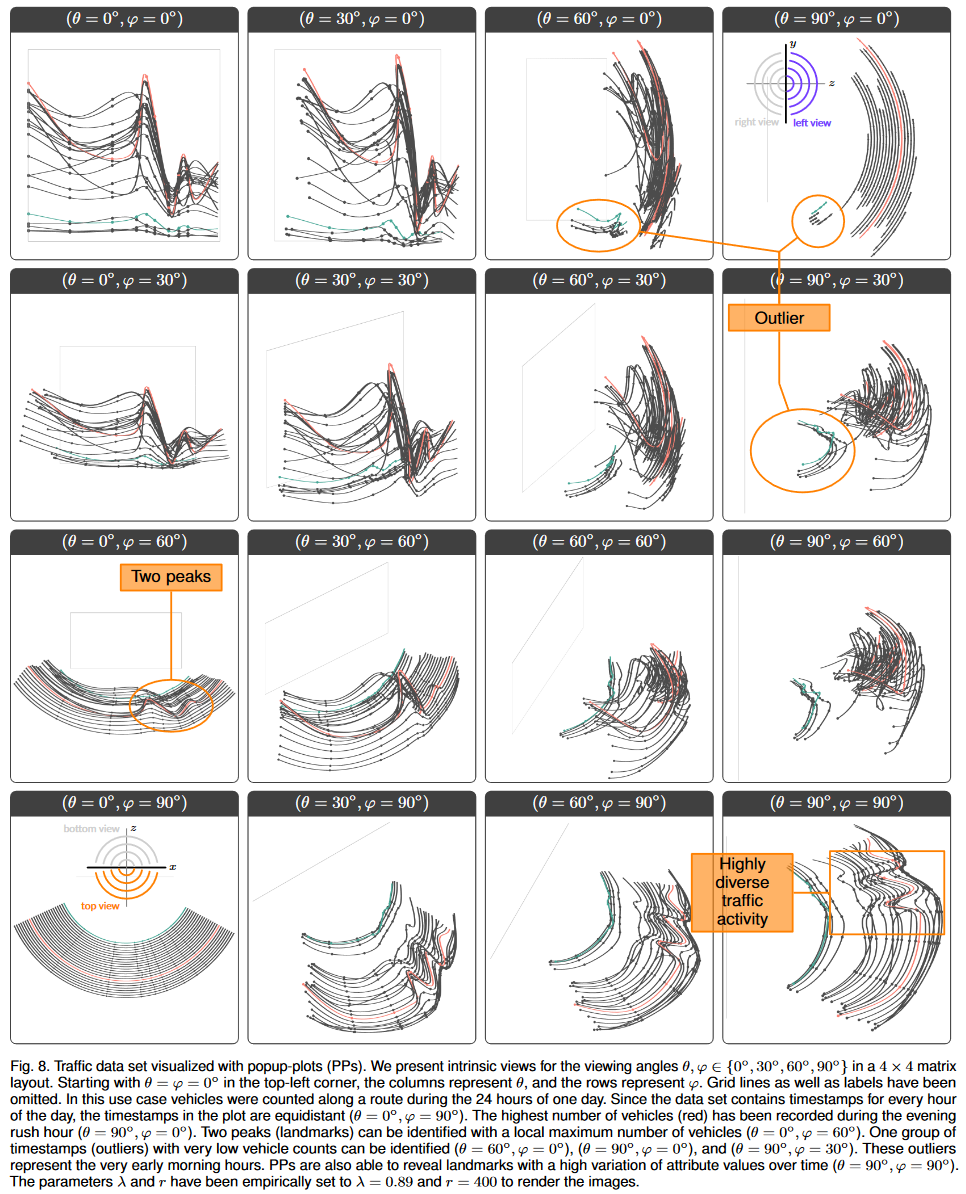
數據中可以識別出兩組（θ = 0°，φ = 0°），其中一大組時間戳記錄了相當高的流量計數，而一組異常值由四個時間戳組成，屬性值較低。我們將車輛數量最多的時間戳標記為紅色，將離群值組的一個時間戳標記為青綠色。當旋轉繪圖查看時間時，可以看到離群值組（Outlier）代表凌晨時段（θ = 60°，φ = 0°）、（θ = 90°，φ = 0°），并且（θ = 90°，φ = 30°）。據報告，晚高峰期間的交通量最高（θ = 90°，φ = 0°）。從側面查看數據，早晚高峰時段清晰可見。還可以看出，車輛數量在早上（一小時內）急劇增加，但在傍晚和夜間時間緩慢減少。數據中的局部最大值表明，特別是兩個地標在高峰時段報告了高車輛數量（兩個峰值）（θ = 0°，φ = 60°）。該數據集包含一天中每小時的流量計數，因此時間戳都是等距的（θ = 0°，φ = 90°）。數據的中間視圖（θ = 90°，φ = 90°）揭示了一些地標的交通計數隨時間的變化（高度多樣化的交通活動）。車輛數量在夜間保持相當恒定，但在白天發生變化。可以通過旋轉 PP 來分析數據中的此類模式，而無需創建額外的孤立視圖。

這些用例展示了 PP 如何允許研究數據的不同方面。從傳統的二維圖（θ = 0°，φ = 0°）開始，通過旋轉可視化來查看時間。當從左側或右側觀察時（例如，θ = 90°，φ = 0°），連續時間戳與最小和最大屬性值之間的距離是可見的。這些視圖呈現了數據的時間發展，時間按圓圈排列。在 PP 的頂部或底部視角（例如，θ = 0°，φ = 90°）中，時間再次被描繪為圓圈，并且地標的位置是可見的。這些視圖中未描述屬性值。 θ 和 φ 的其他值保證了不同視點之間的無縫過渡。

6 評估

我們進行了一項用戶研究，以評估 PP 在分析數據時的潛力。我們的研究包括來自不同領域的 15 名參與者，如軟件開發人員、放射技術專家、統計學家和計算機科學家。關于 3D 可視化參與者的專業水平，八名受訪者表示擁有豐富的經驗，四名受訪者表示擁有一些經驗，三名受訪者表示幾乎沒有經驗。用戶研究已以基于網絡的形式實施。單個評估表的平均完成時間在 8 至 15 分鐘之間。

我們的研究將 PP 與眾所周知的時空立方體概念進行了比較。由于PP提出了一種新穎且創新的概念，并不能立即與既定的接口標準相匹配，因此早期階段的評估很難設計[49]。因此，我們特意以通用的方式設計了用戶研究，以防止評估偏向特定領域。在用戶研究開始時，每個參與者都會收到有關該主題的簡短在線介紹，其中包括一些如何解釋 PP 和時空立方體的建議。在線介紹由一頁內容組成，其中包含描述 PP 主要特征的文本以及補充文本的插圖，其中使用人工數據集來繪制圖表。由于用戶研究是在線完成的，因此用戶可以花盡可能多的時間進行在線介紹。隨后，他們被要求完成三項任務：

T1 從不同的觀察方向識別數據。
T2 描述時間關系。
T3 識別數據中的異常值。

任務 T1 特別涉及方向和轉換（回想表 1）。首先，參與者必須跟蹤視頻序列中的數據峰值，其中時空立方體和 PP 在三個維度上旋轉。其次，他們必須在數據峰值的最后位置放置一個圓形標記。任務 T2 解決時間編碼問題（回想表 1），以便推斷兩個不同時間戳之間的時間關系。在可視化中，兩個時間戳用不同的顏色標記，參與者被要求選擇較早的時間戳。在任務 T3 中，參與者被要求檢測數據中的異常值。異常值之前被定義為與數據集的其余部分表現不同的數據點。參與者可以通過用鼠標繪制區域來標記異常值。只能繪制一個區域，繪制新區域會自動刪除舊區域。任務 T3 旨在測試是否可以以探索性方式使用 PP 來搜索數據中的重大變化或模式。

PP和時空立方體的所有任務都必須完成。我們為每個任務交替使用時空立方體和 PP 的順序。對于任務 T2，PP 和時空立方體使用了不同的顏色，以避免任何相關性。對于每個給定的答案，參與者必須按照 11 點李克特量表對自己的信心進行評分。該研究的實施方式是從可視化中省略參考尺度（例如軸標簽），以最純粹的形式比較兩種可視化。對于 PP，僅將 2D 圖的平面繪制為線框，對于時空立方體，僅將周圍的立方體繪制為線框。通過這種配置，我們測試了參與者是否能夠正確解釋 PP 可視化的橢圓體形狀，即使在沒有網格線和標簽支持的情況下也是如此。

我們使用不同的人工創建的 3D 數據集進行用戶研究。對于任務 T1，我們生成了一個與醫療用例類似的 3D 數據集（參見第 5 節），具有非等距時間戳和九個地標。在兩個地標處，屬性值隨著時間的推移而增加。對于任務 T2 和 T3，我們創建了一個與交通用例類似的 3D 數據集（參見第 5 節），具有等距時間戳和 10 個地標。該數據集包含兩個簇，隨著時間的推移，一個簇的屬性值較低，另一個簇的屬性值較高。

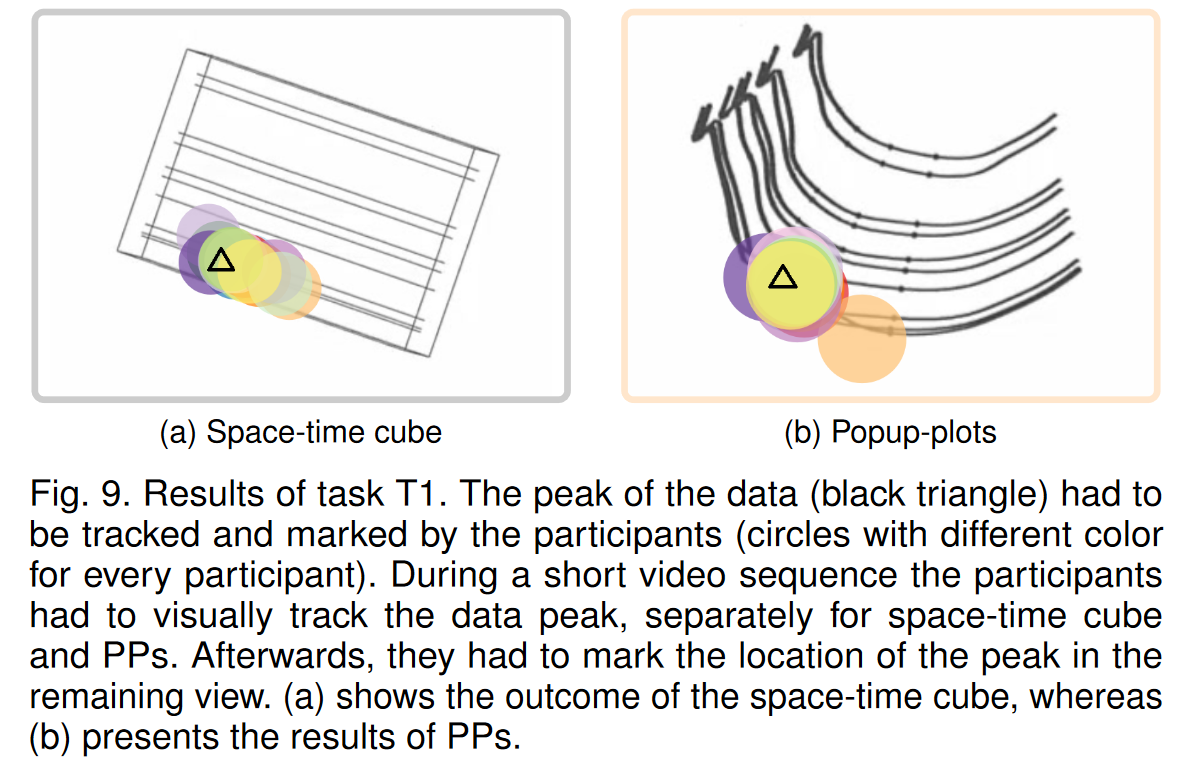
通過對覆蓋數據峰值最終位置的標記進行計數來計算命中率和未命中率來評估任務 T1（參見圖 9）。我們遇到的時空立方體的命中率為 9，而未命中率為 6。PP 的命中率為 14，未命中率為 1。標記位置如圖 9 所示。參與者較少與 PP (9.60 ± 1.06) 相比，使用時空立方體 (8.67 ± 2.53) 時對放置標記更有信心。造成這種情況的原因之一可能是 PP 的無縫過渡，使參與者能夠更好地在視覺上跟蹤峰值。第一項任務的結果表明，所有參與者都能夠正確解釋 PP 的彎曲時空表示，并在旋轉繪圖時正確遵循無縫過渡。

在任務 T2 中（見圖 10），七名參與者進行了猜測（正確率 43%），八名參與者選擇了“我不知道”時空立方體。出現這種結果的原因可能是時空立方體沒有最純粹形式的時間編碼，這得到了置信率 (6.80 ± 2.83) 的支持。對于 PP 可視化，14 名參與者 (93%) 正確選擇了較早的時間戳，只有 1 名參與者 (7%) 選擇了錯誤的時間戳；參與者也非常有信心（9.73 ± 0.59）。 PP 的結果表明，即使沒有標簽或網格線，參與者也能夠正確地將時間的視覺表示解釋為環。因此，PP 的概念似乎很容易理解，即使對于還不熟悉它的用戶來說也是如此。

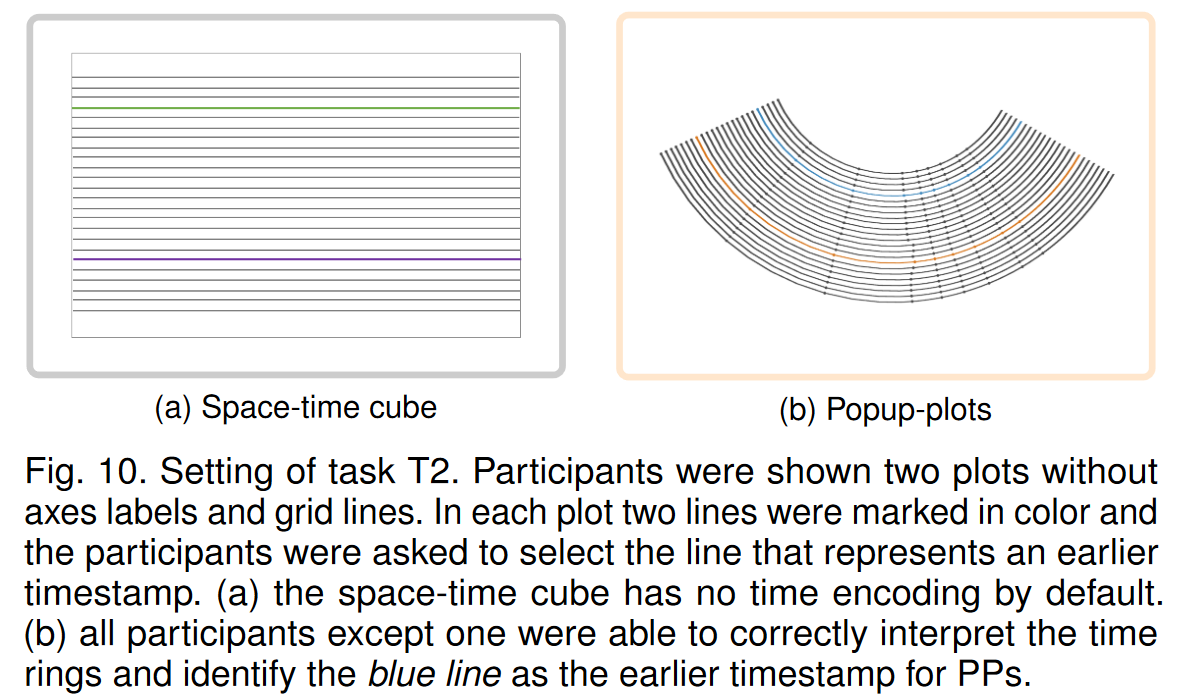
對于任務 T3（參見圖 11），我們計算了標記區域的邊界框和數據中簇的邊界框。準確度定義為標記區域與正確離群區域相比的 Jaccard 指數 [50] 的平均值。時空立方體的結果為 (0.54 ± 0.29)，PP 的結果為 (0.66 ± 0.15)。并非所有參與者都能正確回答，并且在某些情況下，參與者選擇的區域完全超出了實際異常值區域（兩個用于時空立方體，一個用于 PP）。時空立方體 (6.53 ± 3.20) 和 PP (7.40 ± 3.40) 的置信率支持了這一相當平均的結果。然而，結果表明，PP 可以在探索性環境中使用，以搜索數據中有趣的模式。

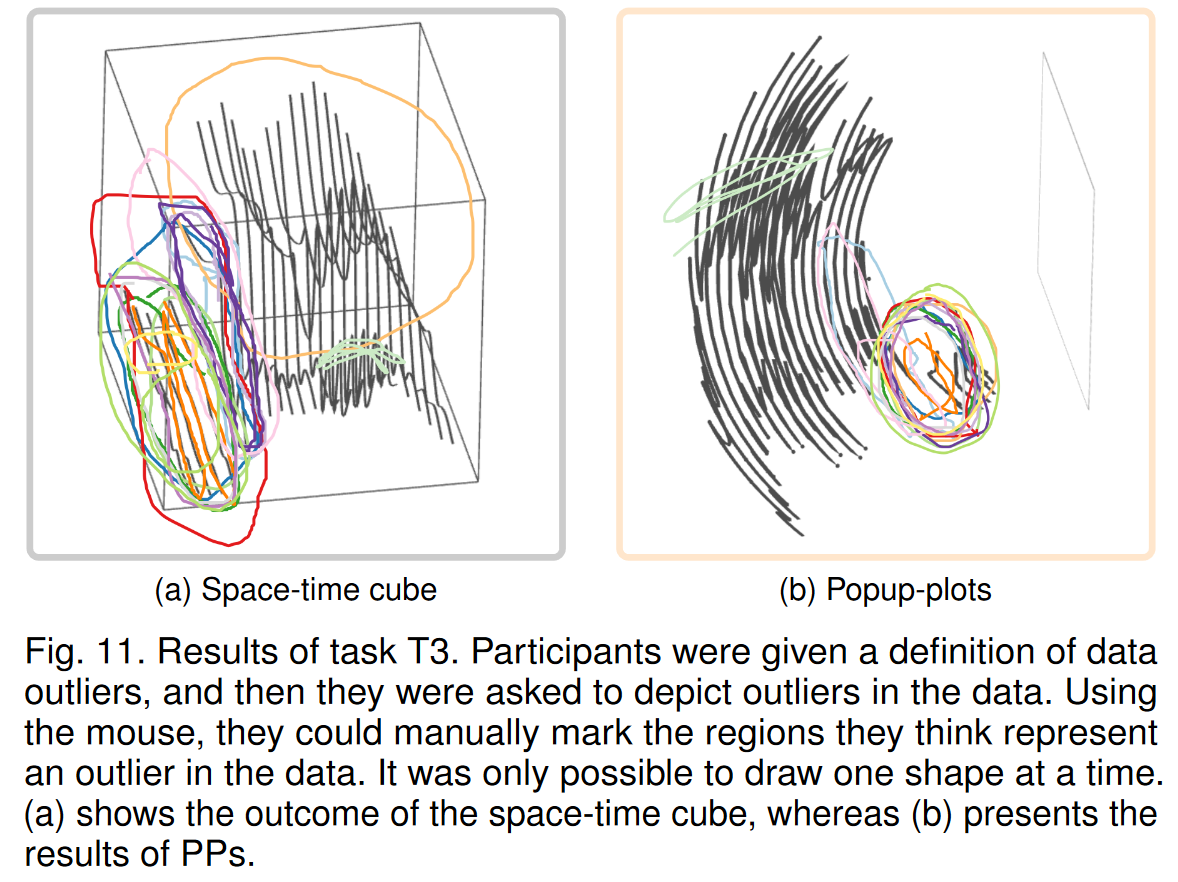
我們通過將參與者分為兩組來進一步評估任務 T1-3 的結果。第一組 (G1) 由已經熟悉 3D 可視化，特別是時空立方體的人員組成（8 名參與者）。相比之下，第二組 (G2) 包括沒有任何 3D 可視化經驗的參與者（7 名參與者）。 G1 組的參與者對所有三項任務的答案表現出稍高的信心，例如，G1 組的 PP 為 (5.33 ± 3.53)，T1 中的時空立方體為 (5.13 ± 3.44)，而 G1 組的參與者則為 (4.27 ± 3.58)。對于 PP，對于 G2 組的 T1 中的時空立方體，為 (3.53 ± 3.62)。可以看到，使用 PP 時置信度的小效應量（Cohen’s d [51]）為 0.30，而在 T1 中使用時空立方體時，置信度的效應量小為 0.45。這兩組之間的結果沒有顯著差異。例如，任務 T3 的結果對于 G1 組來說，PP 為（0.84±0.20），時空立方體為（0.79±0.31），PP 為（0.82±0.21），時空立方體為（0.74±0.32）。 G2組的時間立方體。 PP 的 0.10 和 0.16 的非常小的效應量證實了這一點。可以推斷，即使用戶不熟悉 3D 可視化，也能夠正確解釋數據并完成簡單但通用的任務。

完成任務 T1-3 后，我們要求參與者提供有關 PP 某些特性的定性反饋（回想表 1），同樣按照 11 分李克特量表進行評分。 PP 的環形時間編碼被評為有用 (8.07 ± 1.67) 且易于解釋 (7.80 ± 1.90)。參與者認為無縫過渡是有用的 (7.47 ± 2.17) 和可解釋的 (7.00 ± 2.90)。他們還表示，無縫過渡支持數據探索 (7.33 ± 1.95) 和對時間背景的理解 (7.80 ± 1.97)。參與者進一步報告說，“交互/視圖轉換看起來非常直觀”，并且“樹木年輪的隱喻讓我們很容易記住時間維度”。當被問及他們喜歡的功能時，他們回答“能夠旋轉它們并看到無縫過渡！這可以更好地理解數據的時間維度”。他們進一步認為PP“觀看起來很有趣”并提供“有趣的可能性”。當被問及其他應用場景時，與會者提到PP可以用于“行人計數、運動數據”、“心電圖、腦電圖、股票數據實時可視化”以及“PP可以應用于任何類型的數據測量” 。

7 討論

PP 提供了一種以 3D 方式可視化時態數據的新技術。我們可以證明，通過 PP，我們完全能夠根據自變量時間探索因變量。屬性值的連續和突然變化都清晰可見。通過采用橢圓體模型進行渲染，我們可以在一個視圖中顯示數據，而時間就是交互的問題。

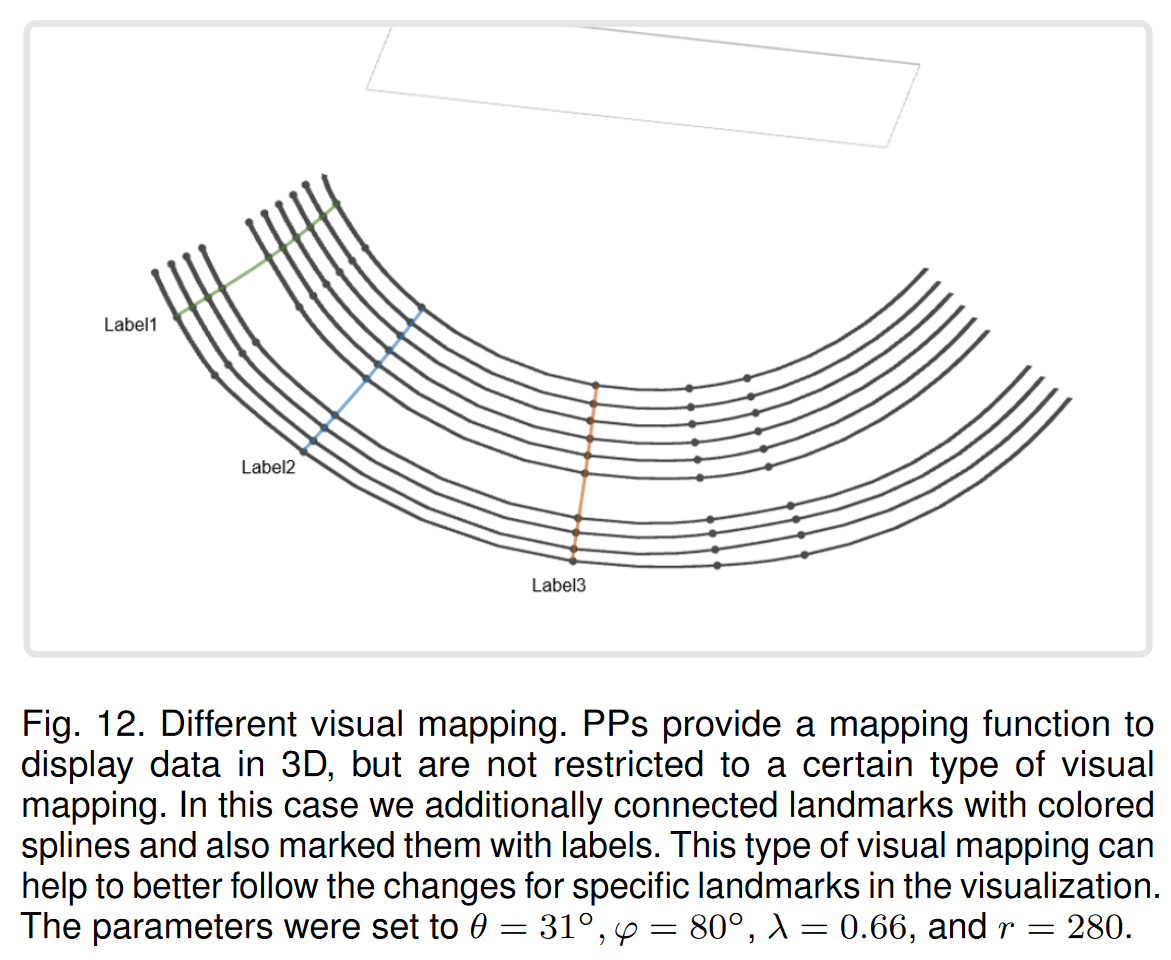
基于這種新方法，可以應用不同的現有視覺映射技術來增強視覺印象并幫助用戶分析數據。在本文中，我們將數據點渲染為球體，并用樣條線連接具有相同時間戳的數據點。根據應用程序領域，其他可視化技術可能更合適。為了說明這一點，我們測試了另一種類型的視覺映射，其中我們還使用樣條線連接了相同地標的數據點（參見圖 12）。我們還可以想象包含特定領域知識的方法，例如，在醫療用例中，可以通過 2D 切片圖像來豐富 PP。特定領域的知識還可以包括突出顯示時間和屬性的關鍵閾值。

我們的方法也有一些局限性。首先，PP 僅限于 3D 數據集，其中一維類似于時間。在時空數據的某些配置中[30]，例如，當將地理地圖作為兩個依賴屬性時，我們的方法可能不像令人滿意的視覺表示。因此，我們的方法不適用于完整分析這些數據。

其次，目前并程的輸入數據必須具有一定的結構。數據需要完整，具有所有時間戳中每個地標的屬性值。在某些應用中，情況可能并非如此，例如，由于傳感器數據丟失。這個問題可以通過在數據點之間進行插值來解決，并在可視化中直觀地突出顯示這些插值。還假設類似于空間（地標）的數據維度是離散的。如果空間是連續的，PP 必須以 3D 方式顯示表面。我們在論文中沒有遇到這樣的數據集，但這是未來探索的一個有趣的方向。

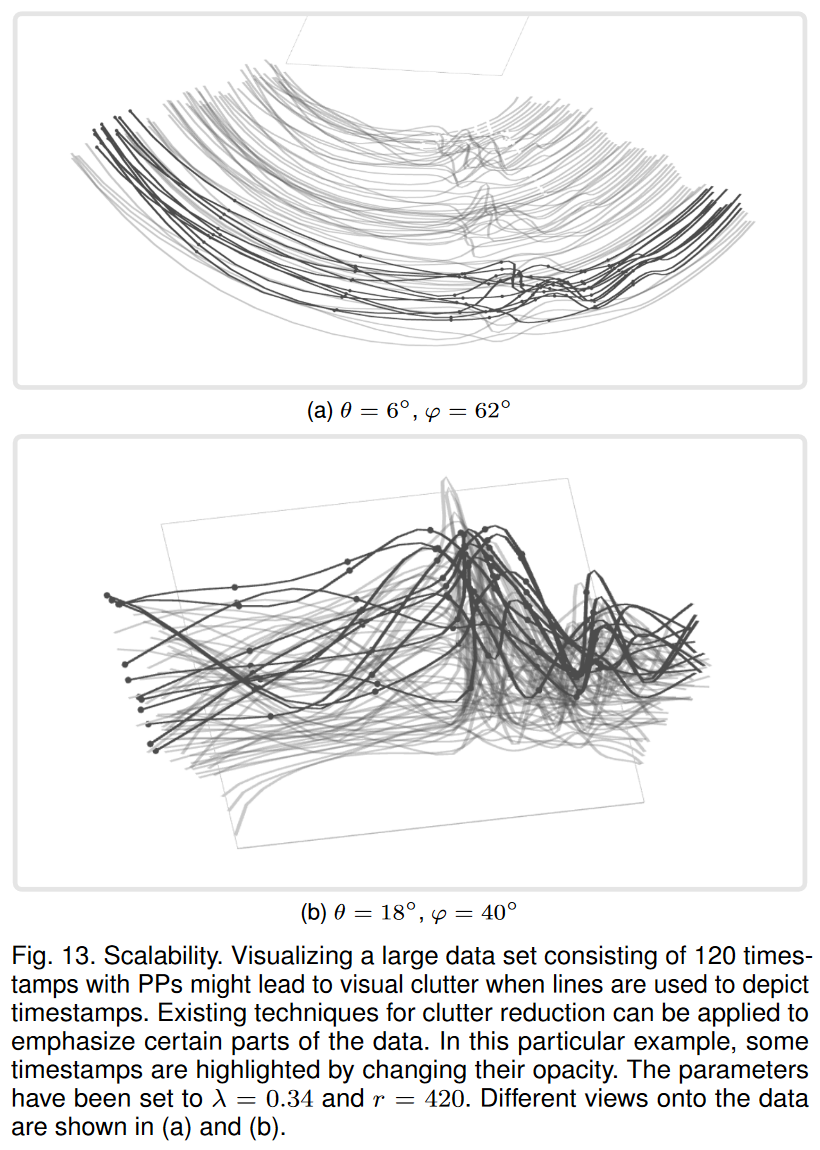
第三，人類只能評估屏幕上的一定量的信息。與平行坐標 [52] 或圖形 [53] 等其他可視化技術類似，如果必須顯示大量數據，PP 可能會變得混亂。由于視覺混亂是可視化中的一個突出主題[54]，其解決方案可以直接轉移到 PP 以增強其視覺表示。為了證明這一點，圖 13 展示了使用 PP 渲染的大型數據集，其中通過根據時間更改樣條線的不透明度來強調一些時間戳。我們使用具有 120 個時間戳的數據集來渲染 PP，參數設置為 λ = 0.34 和 r = 420。一個有趣的挑戰是根據觀看方向正確調整雜波減少技術，因為它們在觀看時可能不適合沿另一個軸的數據。或者，可以使用聚類或數據降維等預處理步驟來減少要顯示的數據量。

PP 提供不同數據視圖之間的無縫轉換。盡管這些轉換可能會給熟悉新可視化技術的用戶帶來額外的認知負擔，但用戶研究中 T1 的結果表明，無縫轉換很容易被用戶理解。另一方面，PP 概念使用戶能夠在單一視圖中分析數據。從這個意義上說，PP 使用戶免于保留對數據的幾種不同視圖的概述以及正確解釋刷動和鏈接技術的額外負擔。

8 結論和未來工作

在本文中，我們提出了彈出圖 (PP)，這是一種可視化包含兩個因變量和自變量時間的 3D 數據集的方法。在這種情況下，兩個因變量被映射到地標和屬性，其中屬性是特定于域的測量，而地標與空間位置相關。 PP 形成了一種新穎的映射技術，可以在三個維度上可視化數據。 PP 通過使用橢球模型彎曲空間，將傳統的二維空間圖和屬性擴展到時間維度。時間的可視化是一個交互問題，由用戶指定的 3D 旋轉控制。根據 PP 的觀察方向，可以研究數據的不同方面。橢球模型保證旋轉過程中的平滑過渡。我們將我們的技術應用于醫學和交通分析的兩個數據集，以評估我們方法的多功能性。

對于未來的工作，我們希望增強我們方法的數據分析功能。不同的視角可用于研究數據的不同方面（例如，θ = 0°、φ = 0° 顯示時間戳）。將來，我們希望自動從數據中提取預定義的查看方向，這可能會讓用戶感興趣，因為它們顯示了數據中的某些模式。這需要評估 3D 數據集的模式識別算法，并估計這些模式最可見的觀看方向。模式也可以從繪圖的拓撲中得出，這與 Lukasczyk 等人的工作類似。 [55]，他使用 Reeb 圖的拓撲來檢測軌跡數據中的熱點。 PP 的可視化會受到兩個參數 λ 和 r 的影響。這些參數能夠可視化具有不同時間粒度的數據集。將來，研究自動查找給定數據集的最佳參數值的技術將會很有趣。

致謝

醫療數據集由斯坦福大學醫學院提供，交通數據集由 AIT Austrian Institute of Technology GmbH 提供。作者感謝 Rosa Mistelbauer 對發展 PP 概念理論的支持。

參考文獻