在前面的機器學習和深度學習的內容中，大量出現了sigmoid函數，所以本篇為大家介紹下sigmoid函數，希望對大家理解前面的算法和后面的Transformer有所幫助

目錄

3.8. sigmoid函數

3.8.1. 定義

3.8.2. 性質

3.8.3. 應用

3.8.4. 缺點

3.8.5. sigmoid函數的導數

3.8.5.1. 導數的定義

3.8.5.2. 導數的性質

3.8.5.3. 導數的應用

3.8.5.4. 注意事項

3.8.6. Python代碼實現

---

3.8. sigmoid函數

3.8.1. 定義

sigmoid函數是一種常見的數學函數，其形狀為“S”形曲線。

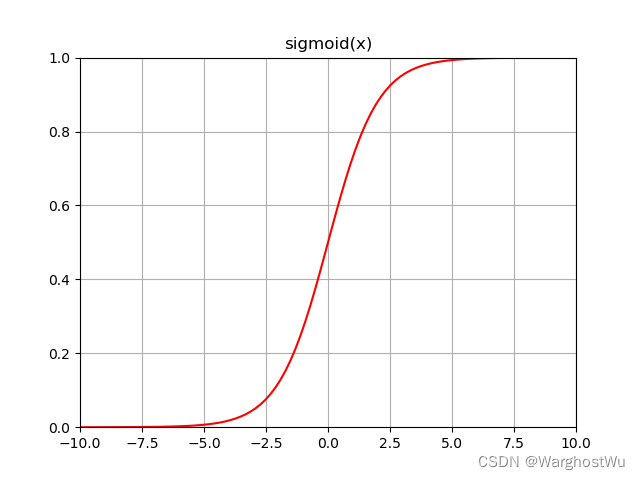
在機器學習和深度學習中，特別是在處理二分類問題時，sigmoid函數被廣泛用作激活函數。

sigmoid函數的數學公式為：

其中，是自然對數的底數（約等于2.71828）。

3.8.2. 性質

• 值域：sigmoid函數的值域為(0, 1)，這意味著無論輸入( x )是什么，輸出總是在0和1之間。這個性質使得sigmoid函數非常適合用于表示概率或者將任意實數映射到(0, 1)區間內。
• 單調性：sigmoid函數在其定義域內是單調遞增的。
• 可導性：sigmoid函數在其定義域內是可導的，這個性質在神經網絡中非常重要，因為它允許我們使用梯度下降等優化算法來訓練網絡。其導數為：

• 形狀：sigmoid函數的形狀類似于“S”，在附近變化較快，而在遠離0的地方變化較慢。這種特性使得sigmoid函數在處理一些需要非線性變換的問題時非常有用。

3.8.3. 應用

1. 二分類問題：在機器學習中，sigmoid函數常用于二分類問題的輸出層，將網絡的輸出轉換為概率值。例如，在邏輯回歸中，sigmoid函數用于將線性回歸的輸出轉換為預測為正類的概率。
2. 神經網絡激活函數：雖然近年來ReLU（Rectified Linear Unit）等激活函數在深度學習中更為流行，但sigmoid函數仍然在某些情況下被用作神經網絡的激活函數，特別是在需要輸出概率或進行二分類的任務中。

3.8.4. 缺點

盡管sigmoid函數有其優點，但在深度學習中作為激活函數時也存在一些缺點：

1. 梯度消失問題：當輸入值遠離0時，sigmoid函數的導數接近于0。在深層神經網絡中，這可能導致梯度在反向傳播過程中迅速減小，使得網絡難以訓練。
2. 計算成本：sigmoid函數涉及指數運算，這在計算上可能相對昂貴，尤其是在大規模數據集和深層網絡上。
3. 非零中心化：sigmoid函數的輸出總是大于0，這意味著在神經網絡中，后續層的輸入總是正的。這可能導致權重更新的不穩定性。

3.8.5. sigmoid函數的導數

sigmoid函數的導數表示了該函數的斜率，即函數值隨輸入變量變化的速率。以下是關于sigmoid函數導數的詳細解釋：

3.8.5.1. 導數的定義

sigmoid函數的導數定義為函數值與其補的乘積，具體公式為：

其中，是sigmoid函數的值。

這個公式表明，sigmoid函數的導數可以通過原函數的值來計算。

3.8.5.2. 導數的性質

• 范圍：sigmoid函數的導數值在0到0.25之間。當輸入值趨近于正無窮或負無窮時，導數值趨近于0；而當輸入值接近0時，導數值接近其最大值0.25。
• 與函數值的關系：導數值與原函數值密切相關。
  • 當sigmoid函數的值接近1或0時，其導數值會變小，表明函數在這些區域的變化率較小。
  • 相反，當接近0.5（即接近0）時，導數值較大，說明函數在這一區域變化較快。

3.8.5.3. 導數的應用

• 神經網絡訓練：在神經網絡中，sigmoid函數的導數對于使用反向傳播算法進行權重更新至關重要。通過計算導數，我們可以了解函數值隨輸入變化的敏感度，并據此調整網絡參數。
• 優化算法：在優化算法中，如梯度下降法，sigmoid函數的導數用于計算損失函數關于模型參數的梯度，從而指導參數更新的方向和步長。

3.8.5.4. 注意事項

雖然sigmoid函數的導數在神經網絡訓練中有其應用，但由于存在梯度消失的問題（即在函數值接近1或0時導數值很小），在深層網絡中可能導致訓練困難。

因此，在實際應用中需要權衡sigmoid函數的優缺點。

3.8.6. Python代碼實現

import numpy as np  def sigmoid(x):  """  計算sigmoid函數值。  參數:  x -- 輸入值，可以是標量、向量或矩陣  返回:  s -- sigmoid函數的值，與輸入x的形狀相同  """  s = 1 / (1 + np.exp(-x))  return s  def sigmoid_derivative(x):  """  計算sigmoid函數的導數。  參數:  x -- 輸入值，可以是標量、向量或矩陣  返回:  ds -- sigmoid函數的導數，與輸入x的形狀相同  """  s = sigmoid(x)  ds = s * (1 - s)  return ds  # 示例用法  
x = np.array([1, 2, 3])  
print("Sigmoid Function Values:")  
print(sigmoid(x))  print("Sigmoid Derivative Values:")  
print(sigmoid_derivative(x))

這段代碼首先定義了兩個函數：sigmoid和sigmoid_derivative。sigmoid函數計算給定輸入x的sigmoid值，而sigmoid_derivative函數則計算sigmoid函數在給定輸入x處的導數。

在示例用法部分，我們創建了一個NumPy數組x，其中包含三個元素，并分別調用了sigmoid和sigmoid_derivative函數來計算這些值的sigmoid函數值和導數。