目錄
1、題目鏈接
2、題目分析
1.狀態表示
?2.狀態轉移方程
?3.初始化
4.填表
5.返回值
3、代碼解析
1、題目鏈接
123. 買賣股票的最佳時機 III
2、題目分析
1.狀態表示
由題目可知，我們分為兩種狀態，買入和賣出，又因為只能完成兩次交易，我們可以畫圖分析：
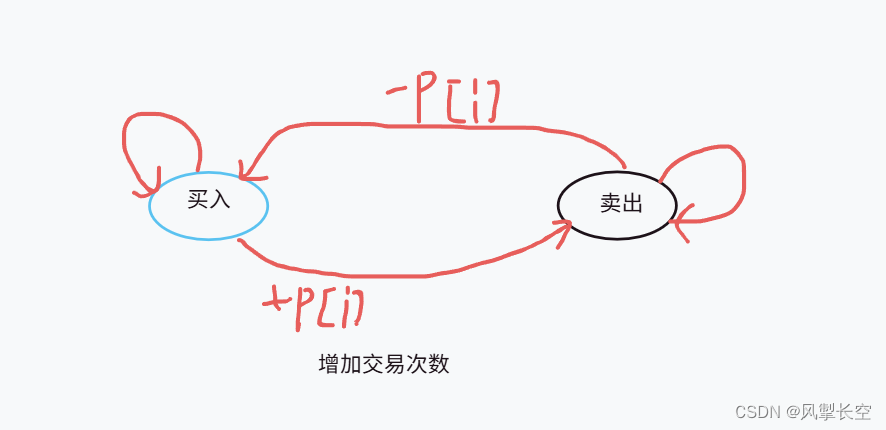
可以看出，從買入到買入，也可以從買入到賣出；
從賣出到賣出，也可以從賣出到買入，但是會增加交易次數；
所以我們用
f[i][j]表示第i天，交易j次后，處于買入狀態的最大利潤
g[i][j]表示第i天，交易j次后，處于賣出狀態的最大利潤
?2.狀態轉移方程
由圖分析：
f[i][j] = max(f[i - 1][j], g[i - 1][j] - prices[i]);
g[i][j] = max(g[i-1][j], f[i - 1][j - 1] + prices[i]);
?關于第二個狀態轉移方程，如果j=0,那么就會有報錯的風險，怎么解決呢？
加個if判斷就好了
g[i][j] = g[i - 1][j];
? ? ? ? ? ? ? ? if (j >= 1) // 如果該狀態存在
? ? ? ? ? ? ? ? ? ? g[i][j] = max(g[i][j], f[i - 1][j - 1] + prices[i]);
只有當j>=1的時候，才執行?g[i][j] = max(g[i][j], f[i - 1][j - 1] + prices[i])，就可以解決這個問題了；
?3.初始化
在第0天，交易0次，處于買入的狀態下，最大利潤是f[0][0]=-p[0];
在第0天，交易0次，處于賣出的狀態下，最大利潤是g[0][0]=0;
注意，在第0天，是不可能出現交易一次或者交易兩次的情況的，所以f[0][1]和f[0][2]是取不到的，所以我們將它設置為無窮小；這可以確保我們后面的計算是正確的；
還要注意，我們設置無窮小和無窮大時，和其他數計算會發生溢出的風險，所以為我們取int最大值的一半0x3f3f3f3f(十六進制)，這樣這個值既可以足夠小，又不會有溢出的風險；
4.填表
按照從上到下，從左到右的順序填表
5.返回值
我們需要返回的是在最后一天得到的最大的利潤，但是不知道交易了幾次，所以，我們要求出最后一天的利潤的最大值
3、代碼解析
int maxProfit(vector<int>& prices) {int n = prices.size();const int INT = 0x3f3f3f3f;vector<vector<int>> f(n, vector<int>(3, -INT));auto g = f;// 初始化f[0][0] = -prices[0], g[0][0] = 0;// 狀態轉移方程// f[i][j]表示第i天，交易j次后，處于買入狀態的最大利潤// g[i][j]表示第i天，交易j次后，處于賣出狀態的最大利潤for (int i = 1; i < n; i++) {for (int j = 0; j < 3; j++) {f[i][j] = max(f[i - 1][j], g[i - 1][j] - prices[i]);g[i][j] = g[i - 1][j];if (j >= 1) // 如果該狀態存在g[i][j] = max(g[i][j], f[i - 1][j - 1] + prices[i]);}}int ret = 0;for (int i = 0; i < 3; i++) {ret = max(ret, g[n - 1][i]);}return ret;
