39. 組合總和

題目🔗

題目描述

給你一個 無重復元素 的整數數組 candidates 和一個目標整數 target ，找出 candidates 中可以使數字和為目標數 target 的 所有 不同組合 ，并以列表形式返回。你可以按 任意順序 返回這些組合。

candidates 中的 同一個 數字可以 無限制重復被選取 。如果至少一個數字的被選數量不同，則兩種組合是不同的。

對于給定的輸入，保證和為 target 的不同組合數少于 150 個。

初始思路

好久沒有做回溯的題了，首先畫圖分析一下：

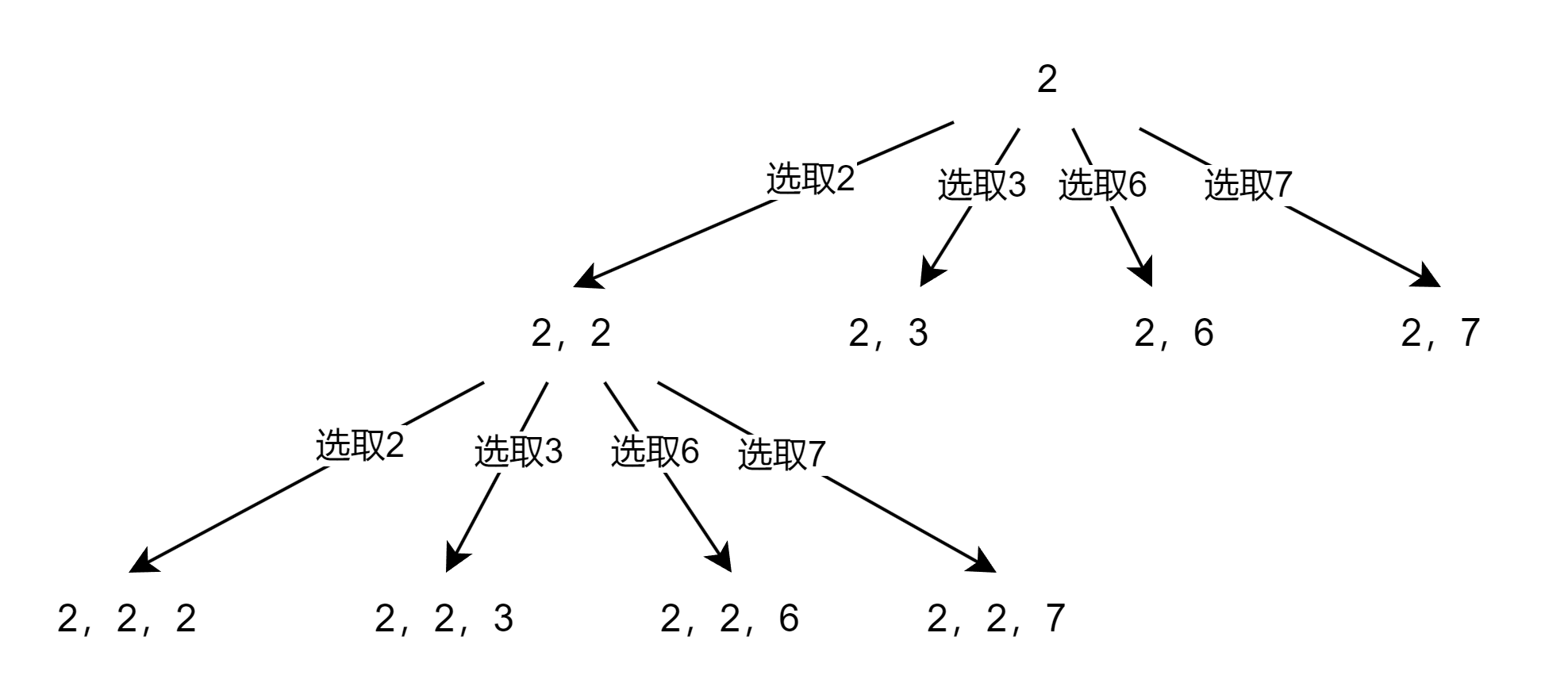
因為這題可以重復選取，那么我們每次選取都是在一個相同的集合中（例如candidates={2, 3, 6, 7}）。所以除了第一次選擇的元素之外，我們之后所做的操作都是相同的，那么就可以定義一個cur_idx來表示我們首次選擇的元素的index，用一個一維數組vec來記錄當前路徑，當vec中的和等于target時，就把這條路徑放入最終結果集result中。于是我開始寫的代碼就是這樣的：

class Solution {
public:void backtracking(int cur_idx, int target, vector<int>& candidates, vector<int>& vec, vector<vector<int>>& results){// 終止條件if(accumulate(vec.begin(), vec.end(), 0)==target){if(find(results.begin(), results.end(), vec)==results.end()) results.push_back(vec);return;}for(int i = 0; i < candidates.size(); i++){if(accumulate(vec.begin(), vec.end(), 0)+candidates[i]<=target)vec.push_back(candidates[i]);backtracking(i+1, target, candidates, vec, results);vec.pop_back();}  }vector<vector<int>> combinationSum(vector<int>& candidates, int target) {vector<int> vec;vector<vector<int>> results;backtracking(0, target, candidates, vec, results);return results;}
};

但是不出意料的沒通過。。

后續分析

還是認真地走一下三部曲吧QAQ

1. 遞歸函數參數
   和我上面分析的一樣：

vector<int>& vec;
vector<vector<int>>& results;
void backtracking(int cur_idx, int sum, int target, vector<int>& candidates);

把vec和results放在類成員變量中，就不用寫在函數入口。sum是當前路徑統計的和。

2. 遞歸終止條件
   
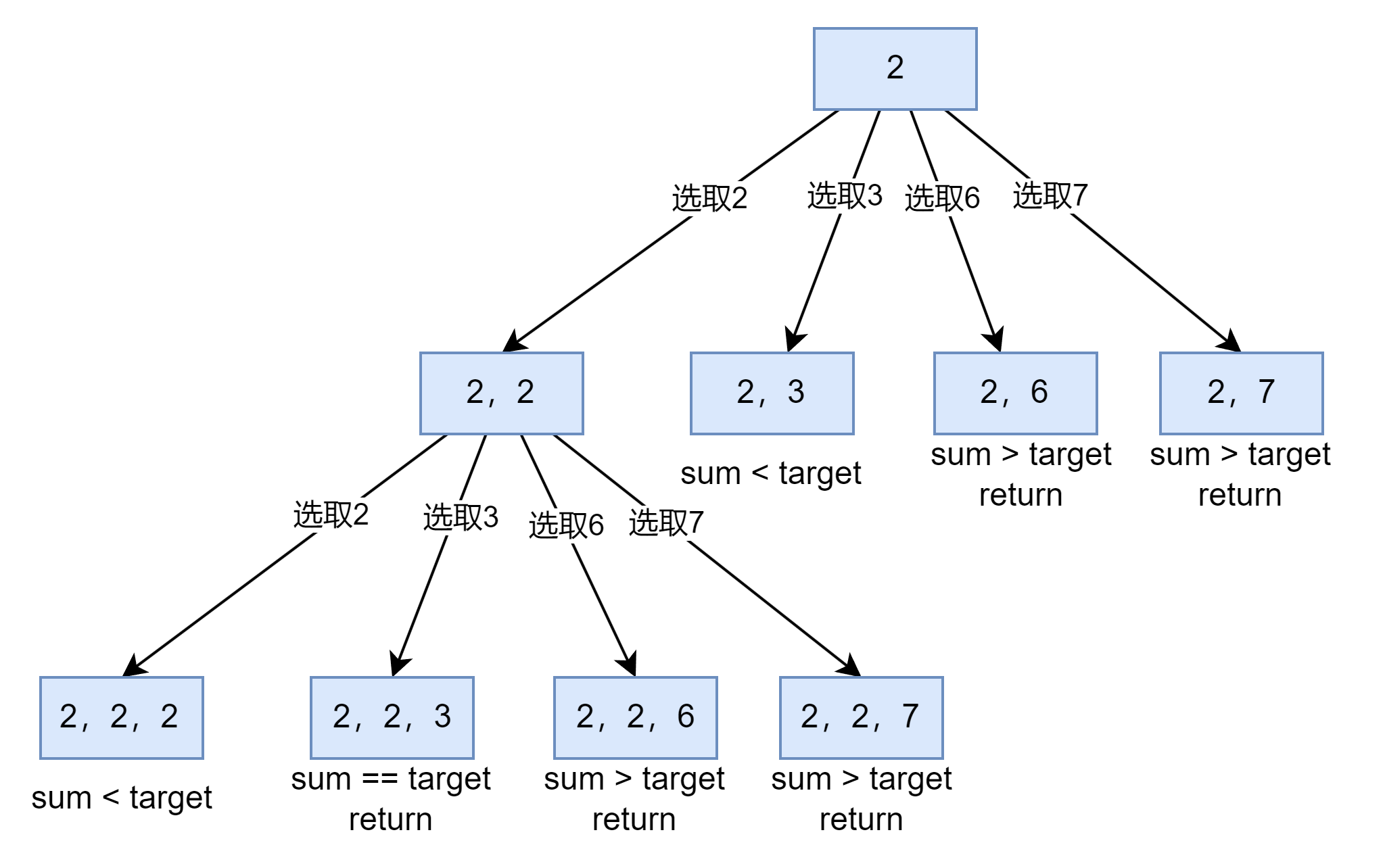
   從上圖來看，當前路徑vec的總和sum大于等于target時，就要返回，并且當sum==target時，我們就要收集結果。

if(sum > target) return;
if(sum == target) {result.push_back(vec);return;
}

啊，可以看出我剛開始忽略了sum>target的情況。

3. 單層搜索邏輯
   這層的重點在于重復選取的實現，先看代碼：

for (int i = cur_idx; i < candidates.size(); i++) {sum += candidates[i];path.push_back(candidates[i]);backtracking(candidates, target, sum, i); // 關鍵點:不用i+1了，表示可以重復讀取當前的數sum -= candidates[i];   // 回溯path.pop_back();        // 回溯
}

整體的邏輯就是我上面這張圖這樣（第二行的{2, 3} sum=5后面應該還有哈，但是我懶得畫了）。

所以整體代碼是：

class Solution {
public:vector<int> vec;vector<vector<int>> results;void backtracking(int cur_idx, int sum, int target, vector<int>& candidates){// 終止條件if(sum == target){results.push_back(vec);return;}if(sum > target) return;// 單層邏輯for(int i = cur_idx; i < candidates.size(); i++){vec.push_back(candidates[i]);sum += candidates[i];backtracking(i, sum, target, candidates);sum -= candidates[i];vec.pop_back();}  }vector<vector<int>> combinationSum(vector<int>& candidates, int target) {vec.clear();results.clear();backtracking(0, 0, target, candidates);return results;}
};

40. 組合總和 II

題目🔗

題目描述

給定一個候選人編號的集合 candidates 和一個目標數 target ，找出 candidates 中所有可以使數字和為 target 的組合。

candidates 中的每個數字在每個組合中只能使用 一次 。

注意：解集不能包含重復的組合。

思路（參考代碼隨想錄）

這題的難點在于集合中有重復元素，但是結果中不能包含重復的組合。

這里我們要明白重復有兩種情況：樹枝重復和樹層重復。

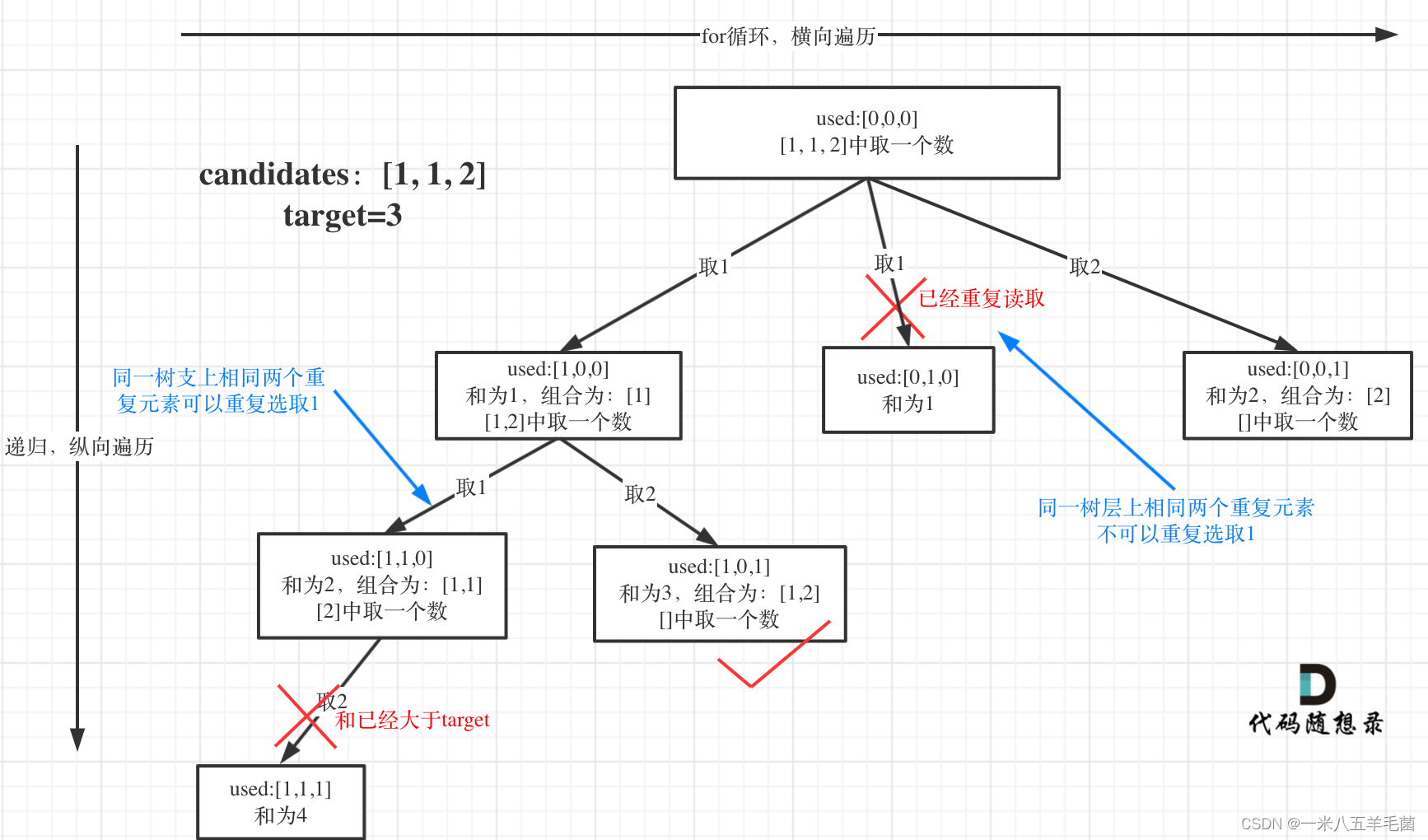
借用卡哥的圖來說明一下。樹枝重復是左邊的情況，樹層重復是中間的情況。而這題不能出現的是樹層重復。這里我們用一個used數組來表示每一個數是否被使用。

從上面這個圖可以看出，當我們在樹的第二層（集合已經被排序過了，相同元素挨在一起），當我們取第二個1的時候，也就是candicates[1]，而前面的candidates[0]也是1，說明已經重復讀取了，所以我們判斷在同一樹層是否重復讀取的邏輯是i > 0 && candidates[i] == candidates[i-1] && used[i-1] == 0。

整體代碼如下：

class Solution {
public:vector<int> path;vector<vector<int>> results;void backtracking(int index, int target, vector<int>& candidates, int sum, vector<int>& used) {if(sum == target) {results.push_back(path);return;}if(sum > target) {return;}for(int i = index; i < candidates.size(); i++) {if(i > 0 && candidates[i] == candidates[i-1] && used[i-1] == 0)continue;sum += candidates[i];path.push_back(candidates[i]);used[i] = 1;backtracking(i+1, target, candidates, sum, used);sum -= candidates[i];path.pop_back();used[i] = 0;}}vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {vector<int> used(candidates.size(), 0);sort(candidates.begin(), candidates.end());path.clear();results.clear();int sum = 0;backtracking(0, target, candidates, sum, used);return results;}
};