說實話，當我看到幾何光學的內容全是初中的解析幾何的時候，我就覺得講的方式太原始了，而且太過復雜也看不懂。所以我嘗試做了數學建模，發現建模之后模型可以解釋一些物理現象，也不會有矛盾的地方，那就算過得去了。換個角度解釋幾何光學有必要嗎？我覺得可以試試，或許有什么意外發現呢？但是這一切依然還是初中的解析幾何，什么都沒改變，僅僅是提供一種思考的角度而已。

? ? ? ?我在看到查閱光學中的畸變的時候，看到了枕形畸變和桶形畸變。

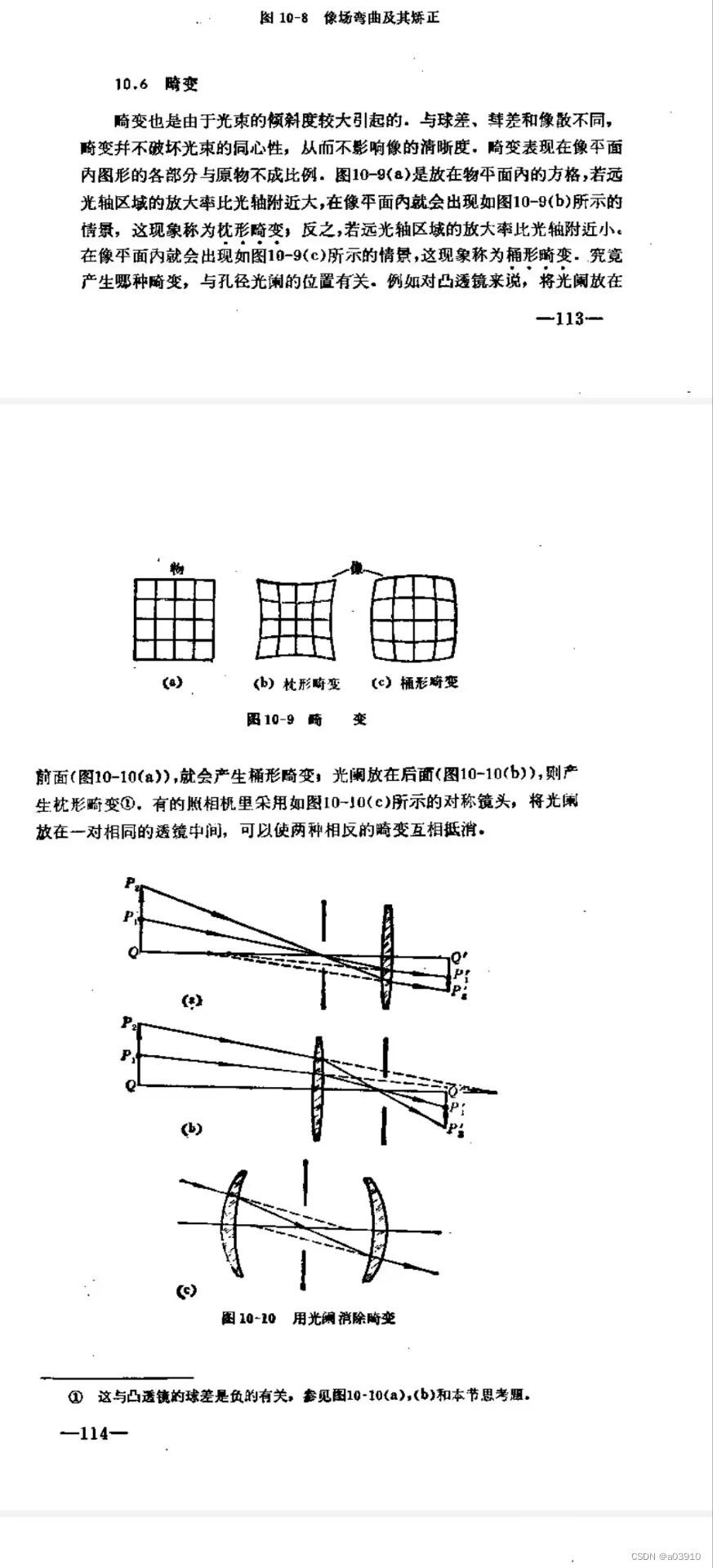
我在想，要想實現枕形畸變，就需要光程的和是固定的，建立橢圓曲線的概念，這個能做到嗎？?

這個真的可以做到，因為光學路徑不在凸透鏡和凹透鏡下不停的改變，? 最終要是能成像，那么這個過程都只是做了同胚變換而已。所以這個光程的路徑大小是可以隨便改的。那么整個圓錐曲線都能寫出來。? ?

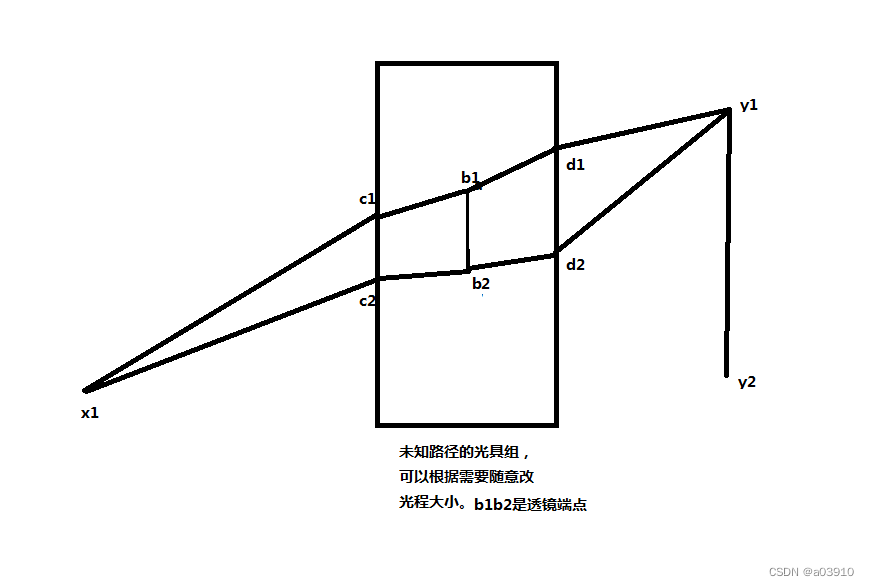
這里假設b1b2是透鏡的最上端點和最小端點，矩形框是我假設的包含某個無窮大的光程的空間區域。所以cibi和bidi的光程可以任意的更改。矩形外部的光程都是正常的按照比例的大小，內部不是。其實外部是歐式空間，內部是非歐式空間的。

現在我想做個橢圓曲線，根據等光程，那么就是x1c1+x1c2=常數。只要內部的不停地修改，然后相應的移動c1和c2的位置即可。并且這種變化可以是隨著x1的改變是連續的。

既然有了橢圓和雙曲線，那么拋物線應該也有。

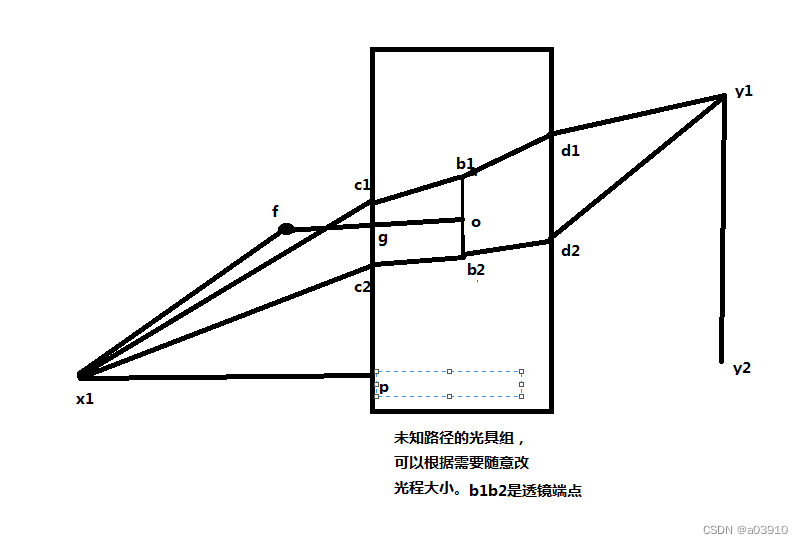
只要令x1p=fg, 那么就能得到拋物線了，只要不停地連續變化內部的光程，滿足x1c1+cd1+d1y1=x1c2+c2d2+d2y1即可。

關鍵是上圖畫出來的只是兩個光線，而不是所有的光線都滿足的情況，如果只是部分光線滿足的話，另外的光線很可能就造成了干擾。所以依然是要問存在性的問題。

在清晰度不高的情況下，不止是可能，是都存在。因為等同區域很寬。可以任意選擇這個區域內的點當做是另外的點。

如果這樣解釋，那就不只是圓錐曲線，任意的曲線都可以了。但是這樣太抽象了，我反而寫不出來什么東西了。暫時就不寫幾何光學的東西了。