Day28:回溯法 491.遞增子序列 46.全排列 47.全排列 II 332.重新安排行程 51. N皇后 37. 解數獨

491. 非遞減子序列

給你一個整數數組?nums?，找出并返回所有該數組中不同的遞增子序列，遞增子序列中?至少有兩個元素?。你可以按?任意順序?返回答案。

數組中可能含有重復元素，如出現兩個整數相等，也可以視作遞增序列的一種特殊情況。

示例 1：

輸入：nums = [4,6,7,7]
輸出：[[4,6],[4,6,7],[4,6,7,7],[4,7],[4,7,7],[6,7],[6,7,7],[7,7]]

示例 2：

輸入：nums = [4,4,3,2,1]
輸出：[[4,4]]

提示：

  • 1 <= nums.length <= 15
  • -100 <= nums[i] <= 100

思路:

本題和求子集相似,要求取有序子集,但子集不能重復,所以就不能將原數組排序后取子集實現去重,本題也是同一父節點下的同層上使用過的元素就不能再使用了

遞歸三部曲:

1.確定返回值和參數的類型

定義兩個全局變量

List<List<Integer>> result;記錄所有結點
? ? List<Integer> node;記錄當前結點

返回值為void,在遞歸過程中更高全局變量

2.確定遞歸結束條件

本題其實類似求子集問題，也是要遍歷樹形結構找每一個節點,但本題收集結果有所不同，題目要求遞增子序列大小至少為2

? if(startIndex>nums.length)
? ? ? ? return;
這行代碼可以省略,因為startIndex在遞歸過程中會加1,不會無限遞歸下去(進不去for循環)?

3.確定單層邏輯

?同一父節點下的同層上使用過的元素就不能再使用了,我們使用set對本層元素去重,注意set只負責本層,所以進入下一層需要清空

將個數大于1的node加入到result

對本層元素去重

遞歸找到所有node

代碼參考:
?

class Solution {List<List<Integer>> result = new  LinkedList<>();List<Integer> path = new LinkedList<>(); public List<List<Integer>> findSubsequences(int[] nums) {backTracking(nums,0);return result;}public void backTracking(int[] nums,int startIndex){if(path.size()>1)result.add(new LinkedList<>(path));if(startIndex == nums.length){return;}Set<Integer> hashSet= new HashSet<>();for(int i=startIndex;i<nums.length;i++){if(!path.isEmpty()&&nums[i]<path.get(path.size()-1)||hashSet.contains(nums[i])){continue;}     hashSet.add(nums[i]);path.add(nums[i]);backTracking(nums,i+1);path.removeLast();}}}

46. 全排列

給定一個不含重復數字的數組?nums?，返回其?所有可能的全排列?。你可以?按任意順序?返回答案。

示例 1：

輸入：nums = [1,2,3]
輸出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

示例 2：

輸入：nums = [0,1]
輸出：[[0,1],[1,0]]

示例 3：

輸入：nums = [1]
輸出：[[1]]

提示：

  • 1 <= nums.length <= 6
  • -10 <= nums[i] <= 10
  • nums?中的所有整數?互不相同

思路:

思路:用回溯法收集葉節點,用uesd數組記錄路徑上哪些數字已經使用,實現路徑去重,這里就不是樹層去重了

遞歸三部曲:

1.確定返回值和參數的類型

定義兩個全局變量List<List<Integer>> result=new ArrayList<>();記錄結果集
? ? List<Integer>path=new LinkedList<>();記錄遞歸路徑,也就是全排列的過程

返回值為void,傳入需要排列 的數組nums,和數組used(記錄遞歸過程中哪些數被用掉了,實現路徑去重)

2.確定遞歸結束條件

? if(nums.length==path.size()){
? ? ? ? ? ? result.add(new ArrayList<>(path));
? ? ? ? ? ? return;
? ? ? ? }

nums.length==path.size()時到達葉節點,也就是找到一組全排列了

3.確定單層邏輯

將路徑上沒用過的數加入路徑

代碼:

class Solution {List<List<Integer>>  result = new LinkedList<>();List<Integer> path = new LinkedList<>();public List<List<Integer>> permute(int[] nums) {boolean[] used = new boolean[nums.length];backTracking(nums,used);return result;}public void backTracking(int[] nums,boolean[] used){if(path.size()==nums.length){result.add(new LinkedList(path));}for(int i=0;i<nums.length;i++){if(used[i]){continue;}path.add(nums[i]);used[i]=true;backTracking(nums,used);used[i]=false;path.removeLast();}}
}

47. 全排列 II

給定一個可包含重復數字的序列?nums?，按任意順序?返回所有不重復的全排列。

示例 1：

輸入：nums = [1,1,2]
輸出：
[[1,1,2],[1,2,1],[2,1,1]]

示例 2：

輸入：nums = [1,2,3]
輸出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

提示：

  • 1 <= nums.length <= 8
  • -10 <= nums[i] <= 10

思路:本題與上一題區別在于,序列nums包含重復數字, 本題該如何去重 呢?

先將數組排序,讓相同的數字排在一起,實現樹層去重,利用used數組實現路徑去重

i>0&&nums[i-1]==nums[i]&&!used[i-1]:說明在同一層使用了,注意這里的used[i-1]必須為false,只有這樣兩個相同的數才會出現在同一層

used[i]:說明該數在路徑中已經使用了,不能再使用了

代碼:

?if(i>0&&nums[i-1]==nums[i]&&!used[i-1]||used[i]){
? ? ? ? ? ? ? ? continue;
? ? ? ? ? ? }

代碼參考:

class Solution {List<List<Integer>> result= new LinkedList<>();List<Integer> path= new LinkedList<>();public List<List<Integer>> permuteUnique(int[] nums) {boolean[] used = new boolean[nums.length];Arrays.sort(nums);backTracking(nums,used);return result;}public void backTracking(int[] nums,boolean[] used){if(nums.length==path.size()){result.add(new LinkedList<>(path));return;}for(int i=0;i<nums.length;i++){if(i>0&&nums[i-1]==nums[i]&&!used[i-1]||used[i]){continue;}used[i]=true;path.add(nums[i]);backTracking(nums,used);used[i]=false;path.removeLast();}}
}

332. 重新安排行程

給你一份航線列表?tickets?，其中?tickets[i] = [fromi, toi]?表示飛機出發和降落的機場地點。請你對該行程進行重新規劃排序。

所有這些機票都屬于一個從?JFK（肯尼迪國際機場）出發的先生，所以該行程必須從?JFK?開始。如果存在多種有效的行程，請你按字典排序返回最小的行程組合。

  • 例如，行程?["JFK", "LGA"]?與?["JFK", "LGB"]?相比就更小，排序更靠前。

假定所有機票至少存在一種合理的行程。且所有的機票 必須都用一次 且 只能用一次。

示例 1：

輸入：tickets = [["MUC","LHR"],["JFK","MUC"],["SFO","SJC"],["LHR","SFO"]]
輸出：["JFK","MUC","LHR","SFO","SJC"]

示例 2：

輸入：tickets = [["JFK","SFO"],["JFK","ATL"],["SFO","ATL"],["ATL","JFK"],["ATL","SFO"]]
輸出：["JFK","ATL","JFK","SFO","ATL","SFO"]
解釋：另一種有效的行程是 ["JFK","SFO","ATL","JFK","ATL","SFO"] ，但是它字典排序更大更靠后。

提示：

  • 1 <= tickets.length <= 300
  • tickets[i].length == 2
  • fromi.length == 3
  • toi.length == 3
  • fromi?和?toi?由大寫英文字母組成
  • fromi != toi

思路:

本題用回溯法,遍歷所有的票的使用順序,由于所有機票至少存在一種合理的行程,我們先將票按照起始位置的開頭字母小的排序,遞歸過程中找到其中一種合理行程就返回,該行程一定是字典排序更小的行程。

遞歸三部曲:

1.確定返回值和參數的類型

使用全局變量保存結果 ,參數傳入所有的票(List<List<String>> tickets),和每張票的使用情況(used[])

由于只取第一個結果,所有返回值類型設置為boolean類型,當找到第一個結果時,就返回true

?List<String> path=new LinkedList<>();
? ? List<String> result;
boolean travel(List<List<String>> tickets,boolean used[])
2.確定遞歸結束條件

當記錄路徑的數組的長度==票的長度+1,說明合理用完了所有票,找到了合理旅游路徑,結束遞歸

? ?if(path.size()==tickets.size()+1){
? ? ? ? ? ? result=new ArrayList<>(path);
? ? ? ? ? ? return true;
? ? ? ? }
3.單層遞歸邏輯

遞歸找到所有方案

?for(int i=0;i<tickets.size();i++){
? ? ? ? ? ? if(!used[i]&&path.get(path.size()-1).equals(tickets.get(i).get(0))){
? ? ? ? ? ? ? path.add(tickets.get(i).get(1));
? ? ? ? ? ? ? used[i]=true;
? ? ? ? ? ? ? //找到第一個方案,結束遞歸
? ? ? ? ? ? if( travel(tickets,used))return true;
? ? ? ? ? ? ? path.remove(path.size()-1);
? ? ? ? ? ? ? used[i]=false;
? ? ? ? ? ? }
?
? ? ? ? }
? ? ? ? return false;
總體代碼:

class Solution {List<String> path=new LinkedList<>();List<String> result;public List<String> findItinerary(List<List<String>> tickets) {boolean[] used=new boolean[tickets.size()];//給票排序Collections.sort(tickets,(a,b)->a.get(1).compareTo(b.get(1)));path.add("JFK");travel(tickets,used);return result;}boolean travel(List<List<String>> tickets,boolean used[]){if(path.size()==tickets.size()+1){result=new ArrayList<>(path);return true;}for(int i=0;i<tickets.size();i++){if(!used[i]&&path.get(path.size()-1).equals(tickets.get(i).get(0))){path.add(tickets.get(i).get(1));used[i]=true;//找到第一個方案,結束遞歸if( travel(tickets,used))return true;path.remove(path.size()-1);used[i]=false;}}return false;}
}


使用本方法因為排序的原因會出現超時?

改進方法:

用Map<出發機場, Map<到達機場, 航班次數>> map來記錄車票,Map<到達機場, 航班次數>為升序TreeMap

class Solution {private Deque<String> path = new LinkedList<>();//雙端隊列,用來存儲飛行路徑private Map<String,Map<String,Integer>> map = new HashMap<>();//hashmap存儲一個其他到其他地方的票數public List<String> findItinerary(List<List<String>> tickets) {for(int i=0;i<tickets.size();i++){//統計每個出發地到目的地的票數if(map.containsKey(tickets.get(i).get(0))){Map<String,Integer> temp= map.get(tickets.get(i).get(0));//獲取目的地們與其對應的票數temp.put(tickets.get(i).get(1),temp.getOrDefault(tickets.get(i).get(1),0)+1);map.put(tickets.get(i).get(0),temp);}else{Map temp = new TreeMap<>();temp.put(tickets.get(i).get(1),1);map.put(tickets.get(i).get(0),temp);}}path.add("JFK");backTracking(tickets.size());return new LinkedList( path);}public boolean backTracking(int tickets){if(path.size()==tickets+1){return true;}String start =  path.getLast();//取出同一出發地點的各個機票的目的地和對應的票數if(map.get(start)!=null)for(Map.Entry<String, Integer> target : map.get(start).entrySet()){int  times= target.getValue();if(times>0){path.add(target.getKey());target.setValue(times-1);if( backTracking(tickets)){return true;}path.removeLast();target.setValue(times);}}return false;}
}

51. N 皇后

按照國際象棋的規則，皇后可以攻擊與之處在同一行或同一列或同一斜線上的棋子。

n?皇后問題?研究的是如何將?n?個皇后放置在?n×n?的棋盤上，并且使皇后彼此之間不能相互攻擊。

給你一個整數?n?，返回所有不同的?n?皇后問題?的解決方案。

每一種解法包含一個不同的?n 皇后問題?的棋子放置方案，該方案中?'Q'?和?'.'?分別代表了皇后和空位。

示例 1：

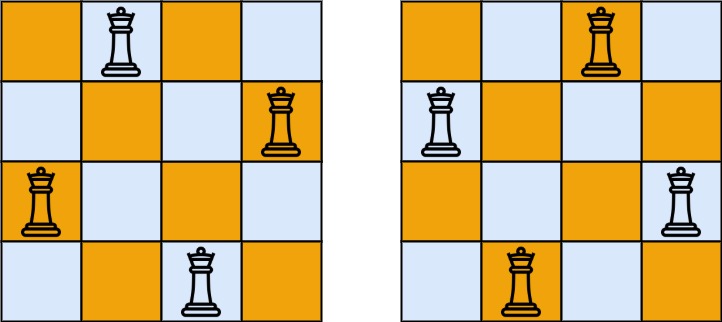
輸入：n = 4
輸出：[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解釋：如上圖所示，4 皇后問題存在兩個不同的解法。

示例 2：

輸入：n = 1
輸出：[["Q"]]

提示：

  • 1 <= n <= 9

皇后們的約束條件：

  1. 不能同行
  2. 不能同列
  3. 不能同斜線

?思路:用回溯法,遍歷出所有可以放置的可能性

遞歸三部曲:

1.確定返回值和參數類型

要把所有能擺放的位置都得出,用全局變量public List<List<String>> result=new ArrayList<>();記錄所有合理的棋盤,返回值為void,傳入棋盤(char[][] chessboard),要放置的皇后在哪一行(int row),棋盤的寬度(n);

?public void backTracking(int n,int row,char[][] chessboard)

2.確定遞歸結束條件

當row==n時,說明所有行都放置了皇后,找到了一種合理放法,將該棋盤存入result中,遞歸結束

?if(row==n){
? ? ? ? ? ?List<String> temp= array2List(chessboard);
? ? ? ? ? ?result.add(temp);
? ? ? ? ? ?return;
? ? ? ?}

3.確定單層遞歸邏輯

遍歷該行的每一個位置并檢查其合理性,如果合理,進入下一行棋盤的擺放

for(int i=0;i<n;i++){
? ? ? ? //如果當前位置合法,就遞歸放下一行
? ? ? ? if(isVaild(chessboard,row,i,n)){
? ? ? ? chessboard[row][i]='Q';
? ? ? ? backTracking(n,row+1,chessboard);
? ? ? ? chessboard[row][i]='.';
? ? ? ? }
? ? ? ?}

class Solution {List<List<String>> result = new LinkedList<>();List<String> board = new LinkedList<>();public List<List<String>> solveNQueens(int n) {char[][] chessboard = new char[n][n];for(char[] c:chessboard){Arrays.fill(c,'.');}backTracking(n,0,chessboard);return result;}public void backTracking(int n,int row,char[][] chessboard){if(row==chessboard.length){List<String> temp= array2List(chessboard);result.add(temp);return;}for(int i=0;i<chessboard.length;i++){if(isVaild(n,chessboard,row,i)){chessboard[row][i]='Q';backTracking(n,row+1,chessboard);chessboard[row][i]='.';}}}//將數組轉為listList<String> array2List(char[][] chessboard){List<String> result=new ArrayList<>();for(int i=0;i<chessboard.length;i++){StringBuilder temp=new StringBuilder();for(int j=0;j<chessboard[0].length;j++){temp.append(chessboard[i][j]);}result.add(temp.toString());}return result;}public boolean isVaild(int n,char[][] chessboard,int row,int col){//檢查列for(int i=row;i>=0;i--){if(chessboard[i][col]=='Q'){return false;}}//45°角for(int i=row-1,j=col+1;i>=0&&j<n;i--,j++){if(chessboard[i][j]=='Q'){return false;}}//135°for(int i=row-1,j=col-1;i>=0&&j>=0;i--,j--){if(chessboard[i][j]=='Q'){return false;}}return true;}
}

37. 解數獨

編寫一個程序，通過填充空格來解決數獨問題。

數獨的解法需?遵循如下規則：

  1. 數字?1-9?在每一行只能出現一次。
  2. 數字?1-9?在每一列只能出現一次。
  3. 數字?1-9?在每一個以粗實線分隔的?3x3?宮內只能出現一次。（請參考示例圖）

數獨部分空格內已填入了數字，空白格用?'.'?表示。

示例 1：

輸入：board = [["5","3",".",".","7",".",".",".","."],["6",".",".","1","9","5",".",".","."],[".","9","8",".",".",".",".","6","."],["8",".",".",".","6",".",".",".","3"],["4",".",".","8",".","3",".",".","1"],["7",".",".",".","2",".",".",".","6"],[".","6",".",".",".",".","2","8","."],[".",".",".","4","1","9",".",".","5"],[".",".",".",".","8",".",".","7","9"]]
輸出：[["5","3","4","6","7","8","9","1","2"],["6","7","2","1","9","5","3","4","8"],["1","9","8","3","4","2","5","6","7"],["8","5","9","7","6","1","4","2","3"],["4","2","6","8","5","3","7","9","1"],["7","1","3","9","2","4","8","5","6"],["9","6","1","5","3","7","2","8","4"],["2","8","7","4","1","9","6","3","5"],["3","4","5","2","8","6","1","7","9"]]
解釋：輸入的數獨如上圖所示，唯一有效的解決方案如下所示：

提示：

  • board.length == 9
  • board[i].length == 9
  • board[i][j]?是一位數字或者?'.'
  • 題目數據?保證?輸入數獨僅有一個解

37. 解數獨

已解答

困難

相關標簽

相關企業

編寫一個程序，通過填充空格來解決數獨問題。

數獨的解法需?遵循如下規則：

  1. 數字?1-9?在每一行只能出現一次。
  2. 數字?1-9?在每一列只能出現一次。
  3. 數字?1-9?在每一個以粗實線分隔的?3x3?宮內只能出現一次。（請參考示例圖）

數獨部分空格內已填入了數字，空白格用?'.'?表示。

示例 1：

輸入：board = [["5","3",".",".","7",".",".",".","."],["6",".",".","1","9","5",".",".","."],[".","9","8",".",".",".",".","6","."],["8",".",".",".","6",".",".",".","3"],["4",".",".","8",".","3",".",".","1"],["7",".",".",".","2",".",".",".","6"],[".","6",".",".",".",".","2","8","."],[".",".",".","4","1","9",".",".","5"],[".",".",".",".","8",".",".","7","9"]]
輸出：[["5","3","4","6","7","8","9","1","2"],["6","7","2","1","9","5","3","4","8"],["1","9","8","3","4","2","5","6","7"],["8","5","9","7","6","1","4","2","3"],["4","2","6","8","5","3","7","9","1"],["7","1","3","9","2","4","8","5","6"],["9","6","1","5","3","7","2","8","4"],["2","8","7","4","1","9","6","3","5"],["3","4","5","2","8","6","1","7","9"]]
解釋：輸入的數獨如上圖所示，唯一有效的解決方案如下所示：

提示：

  • board.length == 9
  • board[i].length == 9
  • board[i][j]?是一位數字或者?'.'
  • 題目數據?保證?輸入數獨僅有一個解

思路:n皇后問題一行只需要放一個皇后,本題一行可能填好幾個數,所以本題是二維遞歸 ,

一個for循環遍歷棋盤的行，一個for循環遍歷棋盤的列，一行一列確定下來之后，遞歸遍歷這個位置放9個數字的可能性！

判斷棋盤是否合法
判斷棋盤是否合法有如下三個維度：

同行是否重復
同列是否重復
9宮格里是否重復

遞歸三部曲:

1.確定返回值和參數類型

只有一個解,只需要找一個解,返回類型為boolean,當回溯返回true時,結束當前遞歸

?Boolean backTracking(char[][] board)

當有多個解時,返回類型為void,需要找遍所有可能

傳入棋盤char[][] board

2.確定遞歸結束條件

本題遞歸不用終止條件，解數獨是要遍歷整個樹形結構尋找可能的葉子節點就立刻返回。

遞歸的下一層的棋盤一定比上一層的棋盤多一個數，等數填滿了棋盤自然就終止（填滿當然好了，說明找到結果了），所以不需要終止條件！

3.確定當層邏輯

一個for循環遍歷棋盤的行，一個for循環遍歷棋盤的列，一行一列確定下來之后，遞歸遍歷這個位置放9個數字的可能性！

class Solution {public void solveSudoku(char[][] board) {backTracking(board);}
public Boolean backTracking(char[][] board){for(int i=0;i<9;i++){for(int j=0;j<9;j++){if(board[i][j]!='.')continue;for(char c='1';c<='9';c++){if(isVaild(i,j,c,board)){board[i][j]=c;if( backTracking(board)) return true;;board[i][j]='.';}}return false;}}return true;
}Boolean isVaild(int row,int col,char val,char[][] board){//同行是否重復for(int i=0;i<9;i++){if(board[row][i]==val){return false;}}//同列是否重復for(int i=0;i<9;i++){if(board[i][col]==val){return false;}}//9宮格內是否重復int startRow=row/3*3;int startCol=col/3*3;for(int i=startRow;i<startRow+3;i++){for(int j=startCol;j<startCol+3;j++){if(board[i][j]==val){return false;}}}return true;}
}

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/diannao/35598.shtml
繁體地址，請注明出處：http://hk.pswp.cn/diannao/35598.shtml
英文地址，請注明出處：http://en.pswp.cn/diannao/35598.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！

相關文章

Atcoder ABC359E Water Tank 題解

Atcoder ABC359E Water Tank 題解

題目傳送門 題解 分析 分類討論。 記第 i i i 個答案為 a n s i 1 ans_i1 ansi?1。 第 i i i 個數就是目前的最大值。 顯然&#xff0c; a n s i h i i ans_ih_i \times i ansi?hi?i。第 i i i 個數就是目前的最大值。 記 l a s t i last_i lasti? 為 i i i …
閱讀更多...
網絡安全學習路線圖（2024版詳解）

網絡安全學習路線圖（2024版詳解）

近期&#xff0c;大家在網上對于網絡安全討論比較多&#xff0c;想要學習的人也不少&#xff0c;但是需要學習哪些內容&#xff0c;按照什么順序去學習呢&#xff1f;其實我們已經出國多版本的網絡安全學習路線圖&#xff0c;一直以來效果也比較不錯&#xff0c;本次我們針對市…
閱讀更多...
Java中多態的實現原理解析

Java中多態的實現原理解析

Java中多態的實現原理解析 大家好&#xff0c;我是免費搭建查券返利機器人省錢賺傭金就用微賺淘客系統3.0的小編&#xff0c;也是冬天不穿秋褲&#xff0c;天冷也要風度的程序猿&#xff01;在本文中&#xff0c;我們將深入探討Java中多態的實現原理及其應用。多態是面向對象編…
閱讀更多...
centos中查看服務的日志

centos中查看服務的日志

在CentOS中查看服務的日志通常涉及查看系統日志文件&#xff0c;這些文件通常位于/var/log/目錄下。不同的服務可能會有不同的日志文件。以下是一些常見的日志文件和查看它們的方法&#xff1a; 1. **系統日志**&#xff1a;系統日志通常存儲在/var/log/messages或/var/log/sy…
閱讀更多...
學會python——生成日志信息（python實例十二）

學會python——生成日志信息（python實例十二）

目錄 1、認識Python 2、環境與工具 2.1 python環境 2.2 Visual Studio Code編譯 3、生成日志信息 3.1 代碼構思 3.2 代碼示例 3.3 運行結果 4、總結 1、認識Python Python 是一個高層次的結合了解釋性、編譯性、互動性和面向對象的腳本語言。 Python 的設計具有很強的…
閱讀更多...
MySQL serverTimezone=UTC

MySQL serverTimezone=UTC

在數據庫連接字符串中使用 serverTimezoneUTC 是一個常見的配置選項&#xff0c;特別是當數據庫服務器和應用程序服務器位于不同的時區時。這個選項指定了數據庫服務器應當使用的時區&#xff0c;以確保日期和時間數據在客戶端和服務器之間正確傳輸和處理。 UTC&#xff08;協…
閱讀更多...
Vue-雙向數據綁定指令

Vue-雙向數據綁定指令

v-model指令 雙向數據綁定就是當數據設置給表單元素時&#xff0c;修改這個數據會修改表單元素的值&#xff0c; 修改表單元素的值同樣也會修改這個數據 <body><div id"app"><input type"text" v-model"name"><p>{{name…
閱讀更多...
利用 Swifter 加速 Pandas 操作的詳細教程

利用 Swifter 加速 Pandas 操作的詳細教程

利用 Swifter 加速 Pandas 操作的詳細教程 引言 Pandas 是數據分析中常用的庫&#xff0c;但在處理大型數據集時效率可能會較低。Swifter 提供了一種簡便的方法&#xff0c;通過并行處理來顯著加速 Pandas 操作。 Swifter 簡介 Swifter 是一個開源庫&#xff0c;旨在自動優…
閱讀更多...
一個項目學習Vue3---創建一個 Vue 應用

一個項目學習Vue3---創建一個 Vue 應用

步驟1&#xff1a;安裝符合要求的node版本 目前官網要求使用的node.js版本為18.3及其以上 所以我們要安裝node.js 18.3及其以上版本 NVM安裝教程&#xff1a;一個項目學習Vue3---NVM和NPM安裝-CSDN博客 若不想安裝NVM&#xff0c;可以直接下載適合自己的node版本Node.js — …
閱讀更多...
Go 延遲調用 defer

Go 延遲調用 defer

&#x1f49d;&#x1f49d;&#x1f49d;歡迎蒞臨我的博客&#xff0c;很高興能夠在這里和您見面&#xff01;希望您在這里可以感受到一份輕松愉快的氛圍&#xff0c;不僅可以獲得有趣的內容和知識&#xff0c;也可以暢所欲言、分享您的想法和見解。 推薦:「stormsha的主頁」…
閱讀更多...
硬件實用技巧：電阻精度和常用阻值表

硬件實用技巧：電阻精度和常用阻值表

若該文為原創文章&#xff0c;轉載請注明原文出處 本文章博客地址&#xff1a;https://hpzwl.blog.csdn.net/article/details/139986658 長沙紅胖子Qt&#xff08;長沙創微智科&#xff09;博文大全&#xff1a;開發技術集合&#xff08;包含Qt實用技術、樹莓派、三維、OpenCV…
閱讀更多...
Linux Vim最全面的教程

Linux Vim最全面的教程

Vim編輯器概述 Vim是一款功能強大的文本編輯器&#xff0c;廣泛應用于Linux和Unix系統中。它是Vi編輯器的增強版&#xff0c;提供了更多的功能和更好的用戶界面。Vim的特點包括多模式編輯、高度可配置性、豐富的插件生態系統以及強大的文本處理能力。 Vim的基本操作 Vim的基…
閱讀更多...
C++ 20新特性之模塊

C++ 20新特性之模塊

&#x1f4a1; 如果想閱讀最新的文章&#xff0c;或者有技術問題需要交流和溝通&#xff0c;可搜索并關注微信公眾號“希望睿智”。 為什么要引入模塊 在C 20之前&#xff0c;所有的代碼組織都依賴于預處理器和頭文件。這種方式主要存在以下四個問題&#xff1a;一是大型項目中…
閱讀更多...
來了，你的第一個AI智能體

來了，你的第一個AI智能體

為了能直觀的感受AI智能體&#xff0c;最好的方法是親手開發一個智能體&#xff0c;當然&#xff0c;這個智能體不能太復雜&#xff0c;否則難度太大&#xff0c;會打擊我們的熱情的&#xff0c;熱情是很寶貴的資源&#xff0c;必須要小心呵護。 我們在國內AI平臺語聚AI上搭建…
閱讀更多...
Batch入門教程

Batch入門教程

Batch學習在多個領域有不同的應用&#xff0c;但最常見的是在機器學習和教育學習領域。以下是一個關于Batch學習入門的清晰指南&#xff0c;將分別介紹這兩個領域中的Batch學習概念、方法和一些實用信息。 1. 機器學習中的Batch學習 定義與概念 Batch_Size&#xff1a;在機器…
閱讀更多...
RK3588 Android13 TvSetting 中增加 WebView 切換菜單

RK3588 Android13 TvSetting 中增加 WebView 切換菜單

前言 電視產品，客戶要求在設置中設備偏好設置子菜單下增加一個 WebView切換菜單，一開始不知道怎么下手，后來想起來在設置開發者選項里有一個類似的菜單， 去把實現邏輯搞出來應該就ok。 效果圖 TvSetting 部分修改文件清單 packages/apps/TvSettings/Settings/res/values…
閱讀更多...
【吊打面試官系列-Mysql面試題】為表中得字段選擇合適得數據類型

【吊打面試官系列-Mysql面試題】為表中得字段選擇合適得數據類型

大家好&#xff0c;我是鋒哥。今天分享關于 【為表中得字段選擇合適得數據類型】面試題&#xff0c;希望對大家有幫助&#xff1b; 為表中得字段選擇合適得數據類型 字段類型優先級: 整形>date,time>enum,char>varchar>blob,text 優先考慮數字類型&#xff0c;其次…
閱讀更多...
npm-check【實用教程】升級項目中的依賴

npm-check【實用教程】升級項目中的依賴

安裝 npm-check npm i -g npm-check檢查項目中的依賴 npm-check會顯示項目中沒有使用&#xff0c;以及有新版本的依賴 升級項目中的依賴 npm-check -u方向鍵上下可以移動圖中左側的箭頭空格鍵可選中/取消選中標注為 Major Update 和 Non-semver 類的版本&#xff0c;需去官網查…
閱讀更多...
Python課程設計：python制作俄羅斯方塊小游戲

Python課程設計：python制作俄羅斯方塊小游戲

基于python的俄羅斯方塊小游戲 目錄 基于python的俄羅斯方塊小游戲 1.概述 1.1 摘要 1.2 開發背景 1.3 開發環境 1.4 實現功能 2.代碼描述 2.1 模塊導入 2.2 初始化變量 2.3 播放音樂 2.4 創建方塊類 2.5 繪制游戲地圖 2.6 游戲初始化 2.7 繪制有邊框矩形 2.8 …
閱讀更多...
Curator框架的底層原理

Curator框架的底層原理

Curator框架的底層原理主要圍繞以下幾個核心方面&#xff1a; 1. **異步操作**&#xff1a;Curator框架通過異步操作來提高性能和可擴展性。它使用Future、Callback或Watcher模式&#xff0c;允許在適當的時機返回結果或通知應用程序狀態的變化。 2. **錯誤處理**&#xff1a…
閱讀更多...
最新文章

Copyright @ 2022~2023