????????在機器學習的聚類中，我們通常需要使用距離來進行類的劃分，或者比較不同類之間的各種距離，這里我們介紹西瓜書上所提出的一些距離計算方式。

? ? ? ? 首先介紹一下距離的一些性質：

西瓜書上給出了四條性質，第一個是非負性，這個好理解，一般來說，距離不會產生負值。下面三條我們結合著例子解釋，如下圖：

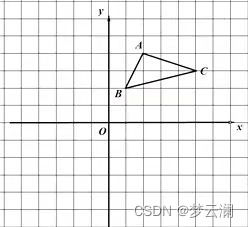
????????我們看圖，這里我們就采用大家都熟悉的歐式距離來說明，第二條距離為零，那肯定就是一個點的距離，比如圖中的A到A的距離；第三條的意思就是A到B的距離等于B到A的距離；第四條就是三角形的兩邊之和大于第三邊，反應到圖上就是B到C的距離小于B到A距離加A到C的距離。

????????接下來介紹距離公式，如圖所示：

第一個公式其實是一個總結的公式，我們令p為2就得到大家熟悉的歐式距離了，至于p為1時的曼哈頓距離，我們看下圖：

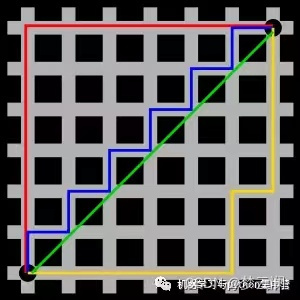
????????圖中的綠色線就是歐式距離，藍線、紅線、黃線都是曼哈頓距離，并且它們的距離都相等，這是為什么呢？其實，曼哈頓距離就是兩點的橫坐標和縱坐標之差再相加，在現實情況中，曼哈頓距離可能會更常用，因為一般情況下兩點之間總會有遮擋物，需要避開。

????????上述說的都是可以直接對“數”進行計算的，那有些不是數值型變量的，我們又該如何進行計算的呢？比如下圖中的變量：

比如圖中這種變量的，我們又該如何計算距離？西瓜書中給出了一種方案：

書中的公式看著好復雜呀，那我們先不看公式，我們先看一個例子：

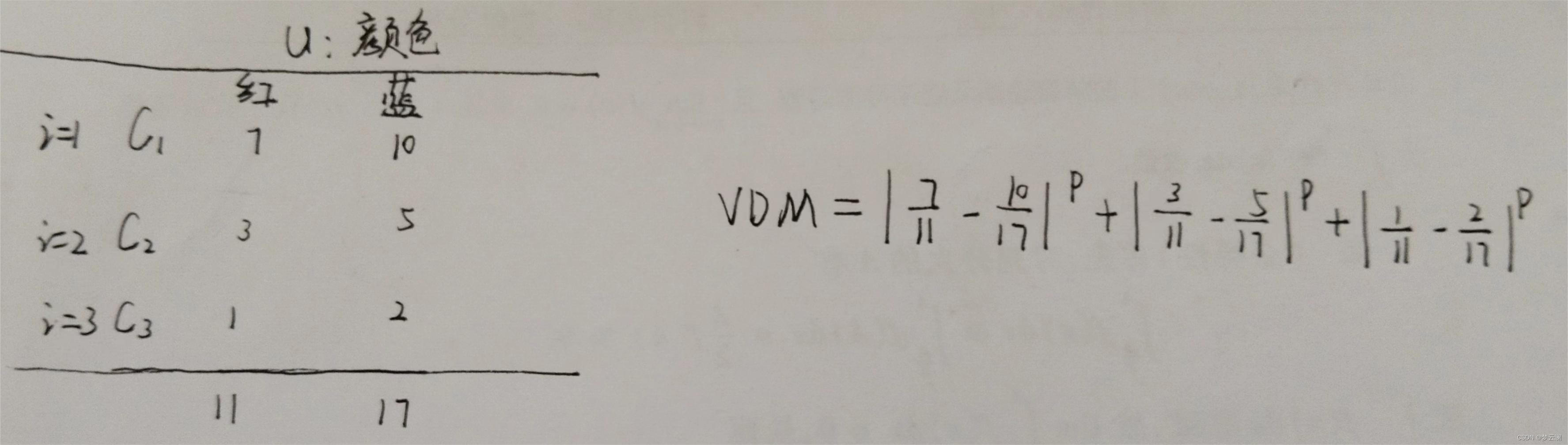
????????我們看圖中，假設說在顏色這個屬性上，有紅色和藍色這兩個值，一共有三個分類，我們看，第一個分類里面有七個紅色，10個藍色，紅色總數有11個，藍色總數有17，那在第一個類里面的距離計算就是紅色的個數除以紅色總數，藍色的個數除以藍色總數，就算出來了，以此類推，其他類也是這樣，再把所有值相加就得出VDM了。

????????現在再回頭看上述的公式，是不是就很簡單啦？

最后我們再介紹兩種變形的公式：

第一個公式就是對于那種既有數值變量也有列名變量混合的計算公式，就是兩種公式混合起來。

第二個公式加了一個權重，可能會有某些樣本值得重要程度不同，所以加了權重，其實和前面距離計算公式差不多。

ok,這篇就到這里啦，歡迎小伙伴們批評指正~（圖片來源于西瓜書和網絡）