五、位運算

常見位運算總結

&：有0就是0；

|：有1就是1

^：相同為0，相異就是1/無進位相加

給定一個數n,確定它的二進制表示中的第x位是0還是1：二進制中權值最小的是第0位，所以int整型是從第0位到第31位。于是n>>x &1就可以了

將一個數n的二進制表示的第x位修改成為1： (1<<x) | n

將一個數n的二進制表示的第x位修改成為0：(~(1<<x)) & n?

提取一個數n的二進制表示中最右側的1：n&(-n)，正數變成負數的二進制表示就是按位取法再加1。-n的本質是將最右側的1的左邊區域（不包括最右側的1也就是當前位置）全部變成相反，其余的都不變。

干掉一個數n二進制表示中最右側的1，也就是將這個1變成0：n&(n-1) ,n-1的本質是將最右側的1右邊的區域（包含1）全部變成相反。

異或：a^a=0；a^0=a；a^b^c=a^(b^c)；交換律；采用無進位相加很容易證明?

?1.判斷字符是否唯一

采用位圖的思想：因為單獨的一個整型變量就有32位比特位

優化點：鴿巢原理，也就是如果字符串的長度超過26，必定存在重復字符。

class Solution {
public:bool isUnique(string astr) {//利用鴿巢原理進行優化if(astr.size()>26) return false;int bitmap=0;for(auto ch:astr){//判斷字符出現在哈希表中if((1<<(ch-'a')) & bitmap) return false;//將當前字符加入到位圖中else bitmap+=(1<<(ch-'a'));//bitmap |= (1<<(ch-'a'))}return true;}
};

2.丟失的數字

class Solution {
public:int missingNumber(vector<int>& nums) {int n=nums.size()+1;int result=0;for(auto ch:nums) result^=ch;for(int i=0;i<n;i++) result^=i;return result;}
};

3.兩整數之和（巧妙）

利用異或的無進位相加，然后找到需要進位的地方。通過a&b可以找到需要進位的地方，因為只有1&1才能得到1，而這也是我們需要進位的地方。（a&b)<<1才是我們需要進位的位置。

class Solution {
public:int getSum(int a, int b) {while(b){int temp_a=a;a=temp_a^b;//先算出無進位相加的結果b=(temp_a&b)<<1;//算出進位}return a;}
};

4.只出現一次的數字

?

class Solution {
public:int singleNumber(vector<int>& nums) {int ret=0;for(int i=0;i<32;i++)//依次去修改ret中的每一位{int sum=0;//統計nums中第i比特位出現1的次數for(auto ch:nums)if(ch & (1<<i)) sum++;if(sum%3) ret |= (1<<i);//修改ret的第i比特位}return ret;}
};

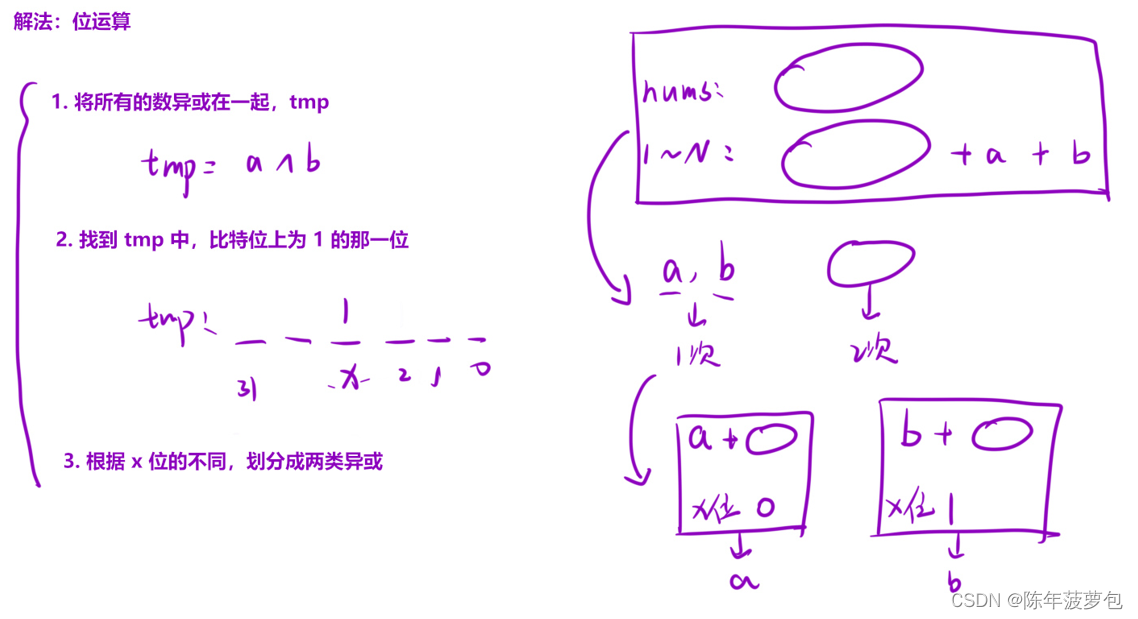
5.消失的兩個數

??

class Solution {
public:vector<int> missingTwo(vector<int>& nums) {vector<int> result;//將所有的數全部都異或到一起int tmp=0;int n=nums.size();for(auto ch:nums) tmp^=ch;for(int i=1;i<=n+2;i++) tmp^=i;//找到tmp中，比特位為1的那一位pos，在該比特位上a和b的比特值是不一樣的。int pos;for(pos=0;pos<32;pos++) if((tmp>>pos)&1) break;//根據pos位的不同，劃分成為兩類來異或int a=0,b=0;for(auto ch:nums){if((ch>>pos)&1) a^=ch;else b^=ch;}for(int i=1;i<=n+2;i++){if((i>>pos)&1) a^=i;else b^=i;}return {a,b};}
};

六、模擬算法

模擬算法就是依葫蘆畫瓢，思路比較簡單，但是算法流程存在很多細節，將流程轉換成為算法有比多要注意的細節。模擬題找優化一般都是通過找規律進行的。

6.替換所有的問號

class Solution {
public:string modifyString(string s) {int n=s.size();//遍歷字符串for(int i=0;i<n;i++){//找到？字符if(s[i]=='?'){//遍歷26個字母替換該字符for(char ch='a';ch<='z';ch++){//找到符合要求的字符，下面的if條件是關鍵if((i==0 || ch!=s[i-1]) && (i==n-1 || ch!=s[i+1])){s[i]=ch;break;}}}}return s;}
};

7.提莫攻擊

?

class Solution {
public:int findPoisonedDuration(vector<int>& timeSeries, int duration) {int result=0;for(int i=0;i<timeSeries.size()-1;i++){if(timeSeries[i+1]-timeSeries[i]>=duration) result+=duration;else result+=(timeSeries[i+1]-timeSeries[i]);}return result+duration;}
};

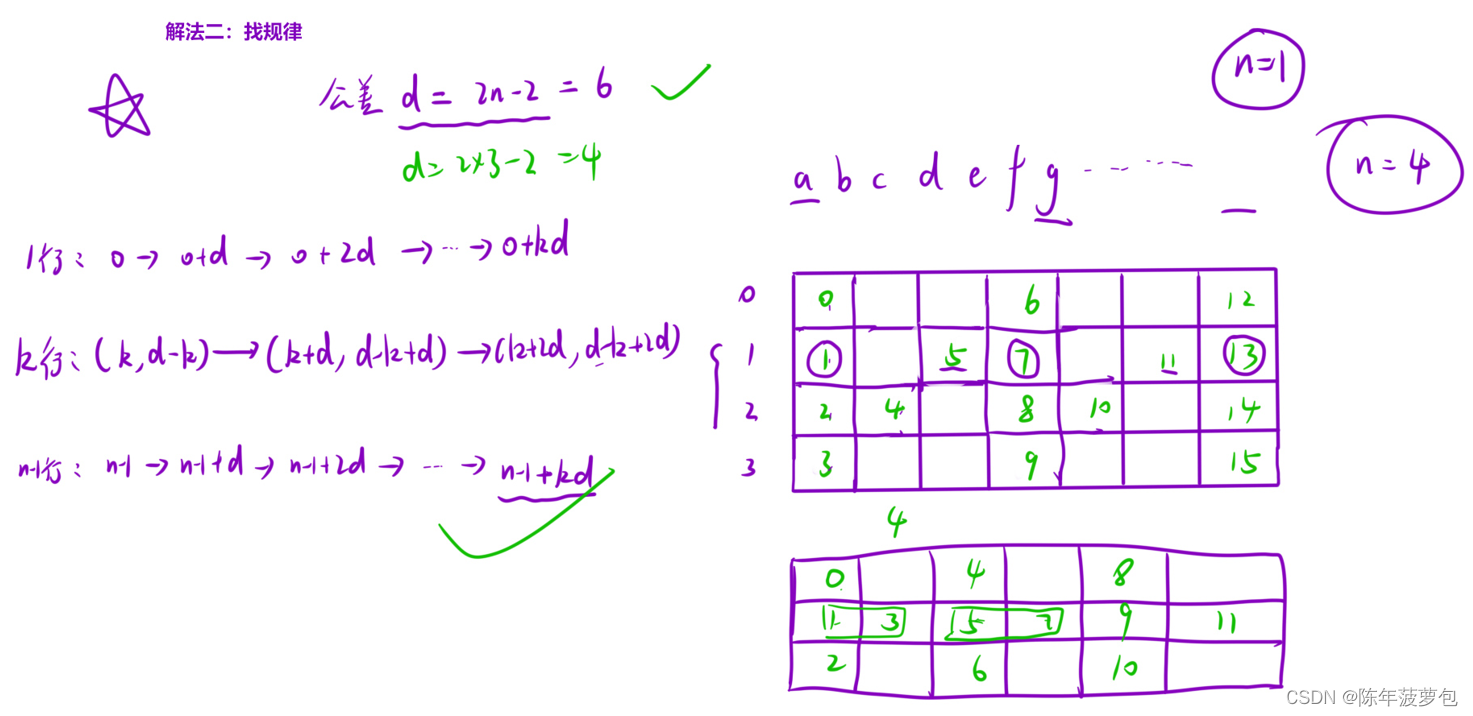
8.Z字形變換

class Solution {
public:string convert(string s, int numRows) {//處理邊界情況if(numRows==1) return s;string result;int n=s.size();int d=numRows*2-2;//公差d//1.先處理第一行for(int i=0;i<n;i+=d){result+=s[i];//}//2.處理中間行for(int k=1;k<numRows-1;k++)//枚舉每一行{for(int i=k,j=d-k;i<n || j<n;i+=d,j+=d)//注意不要將i<n || j<n寫成了i<n && j<n{if(i<n) result+=s[i];if(j<n) result+=s[j];}}//3.最后處理最后一行for(int i=numRows-1;i<n;i+=d){result+=s[i];}return result;}
};

9.外觀數列

class Solution {
public:string countAndSay(int n) {string result="1";if(n==1) return result;for(int i=1;i<n;i++)//翻譯n次{string tmp;int len=result.size();//采用雙指針來進行翻譯for(int left=0,right=0;right<len;){while(right<len && result[left]==result[right]) right++;//當right=len-1的邊界情況也可以正確處理tmp+=to_string(right-left);//to_string函數處理下標left和right的值不同的時候tmp+=result[left];left=right;}result=tmp;}return result;}
};

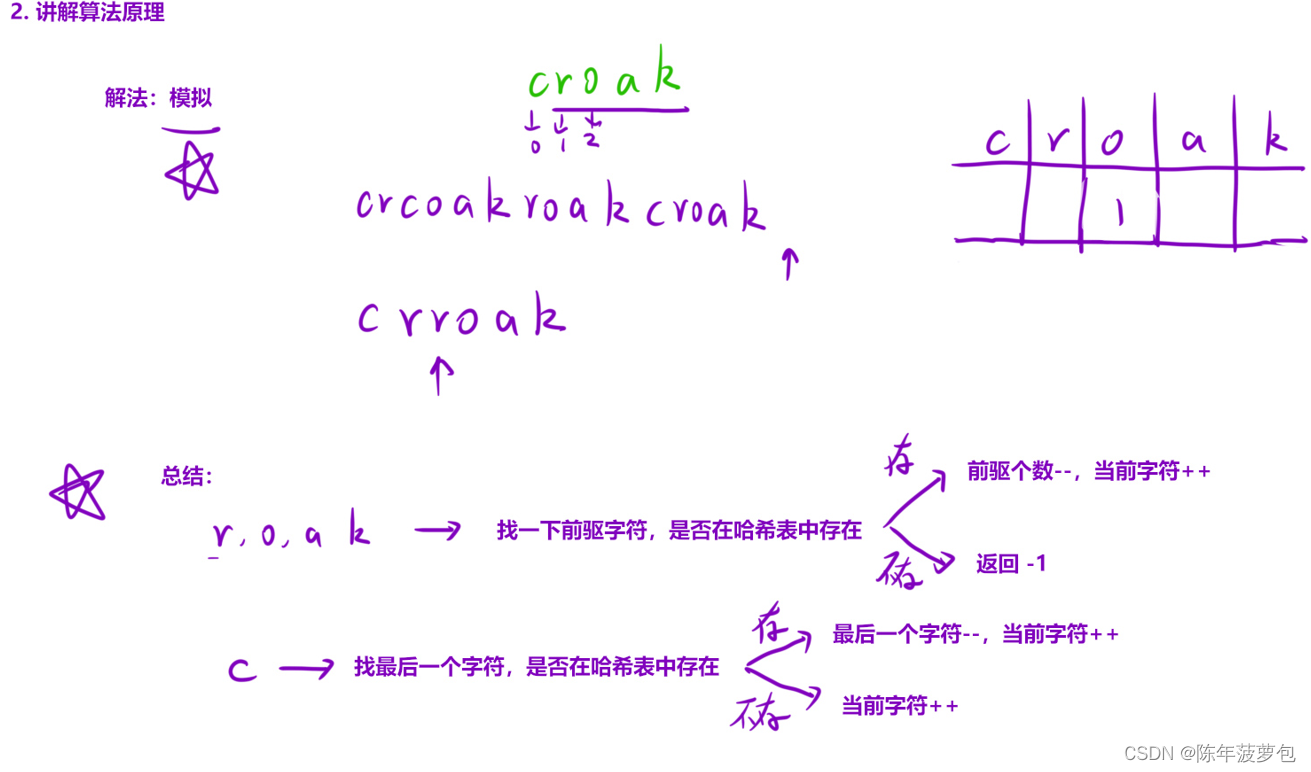
10.數青蛙

上述總結就是代碼的邏輯非常重要

class Solution {
public:int minNumberOfFrogs(string croakOfFrogs) {string t="croak";int n=t.size();vector<int> hash(n);//用數組來模擬哈希表unordered_map<char,int> index;//存儲t字符串每個字符char以及對應的下標intfor(int i=0;i<n;i++) index[t[i]]=i;//遍歷字符串for(auto ch:croakOfFrogs){//1、如果ch不在字符串t的范圍內if(index.count(ch)==0) return -1;//2、如果字符ch不是c并且前面并沒有匹配的字符if(ch!=t[0] && hash[index[ch]-1]<1) return -1;//3、正常運作if(ch==t[0] && hash[n-1]<1) hash[0]++;else if(ch==t[0] && hash[n-1]>=1) hash[0]++,hash[n-1]--;else hash[index[ch]]++,hash[index[ch]-1]--;}for(int i=0;i<n-1;i++) if(hash[i]!=0) return -1;return hash[n-1];}
};

七、分治

分治就是分而治之，將一個大問題轉換成為若干個相同或者相似的子問題，直到劃分到子問題可以快速解決為止。

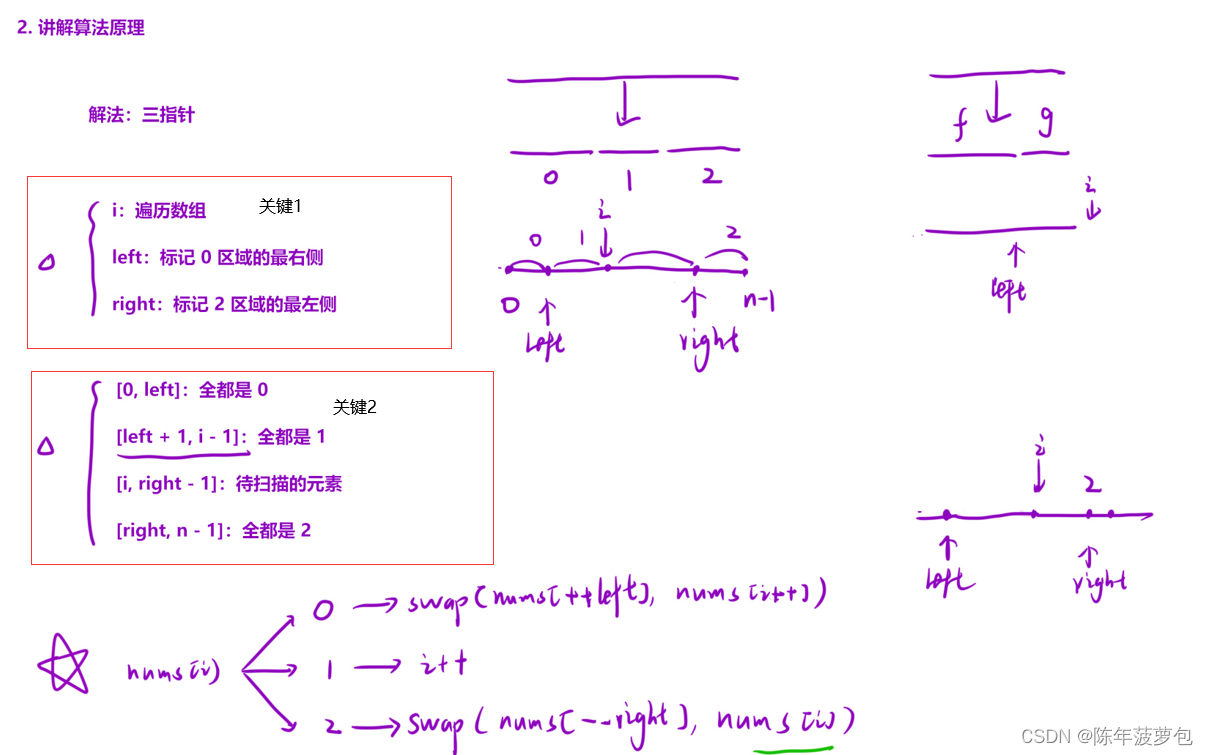
10.顏色分類(快排關鍵）

?

class Solution {
public:void sortColors(vector<int>& nums) {int n=nums.size();int left=-1,right=n;for(int i=0;i<right;)//條件是i<right不是i<n，這是一個易錯點。{if(nums[i]==0) swap(nums[++left],nums[i++]);else if(nums[i]==1) i++;else swap(nums[--right],nums[i]);}}
};

?11.排序數組 （快排）

class Solution {
public:int getrandom(vector<int>& nums,int left,int right){int r=rand();return nums[r % (right-left+1) + left];}void sortArray_help(vector<int>& nums,int l,int r){//定義遞歸出口if(l>=r) return;//隨機方式選擇基準元素int standar=getrandom(nums,l,r);int left=l-1;int right=r+1;//分成三塊for(int i=l;i<right;){if(nums[i]<standar) swap(nums[++left],nums[i++]);else if(nums[i]==standar) i++;else swap(nums[--right],nums[i]);  }sortArray_help(nums,l,left);sortArray_help(nums,right,r);}vector<int> sortArray(vector<int>& nums) {srand(time(NULL));//種下一棵隨機數種子sortArray_help(nums,0,nums.size()-1);return nums;}
};

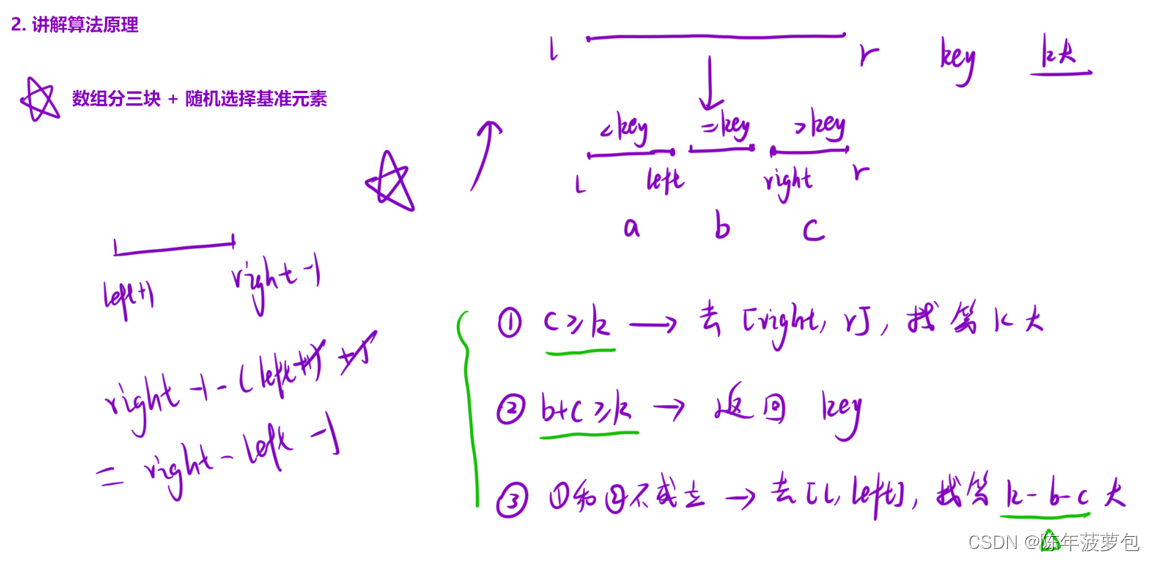
12.數組中的第k個最大元素

class Solution {
public:int getrandom(vector<int>&nums,int left,int right){int r=rand();return nums[r%(right-left+1)+left];}int qsort(vector<int>& nums,int l,int r,int k){if(l==r) return nums[l];//容易遺漏的點//1、隨機選擇基準元素int standard=getrandom(nums,l,r);//2、根據基準元素將數組分成三塊int left=l-1;int right=r+1;int i=l;while(i<right){if(nums[i]<standard) swap(nums[++left],nums[i++]);else if(nums[i]==standard) i++;else swap(nums[--right],nums[i]);}//分情況討論//下面的三個條件判斷是關鍵if(r-right+1>=k) return qsort(nums,right,r,k);else if(r-left>=k) return standard;else return qsort(nums,l,left,k-r+left);}int findKthLargest(vector<int>& nums, int k) {srand(time(NULL));return qsort(nums,0,nums.size()-1,k);}
};

13.最小k個數（未做）

14.歸并排序（歸并排序）

class Solution {
public:vector<int> tmp;//輔助數組用來排序void mergesort(vector<int>& nums,int left,int right){if(right<=left) return;//1、選擇中間點劃分區間int mid=(left+right)/2; //2、將左右區間排序int left1=left;int right1=mid;int left2=mid+1;int right2=right;mergesort(nums,left1,right1);mergesort(nums,left2,right2);int i=0;//3、合并兩個有序數組while(left1<=right1 && left2<=right2) tmp[i++]=nums[left1]<=nums[left2]?nums[left1++]:nums[left2++];//4、處理沒有遍歷完的數組while(left1<=right1) tmp[i++]=nums[left1++];while(left2<=right2) tmp[i++]=nums[left2++];//5、還原for(int i=left;i<=right;i++) nums[i]=tmp[i-left];     }vector<int> sortArray(vector<int>& nums) {tmp.resize(nums.size());mergesort(nums,0,nums.size()-1);return nums;}
};

15.交易逆序對的總數（未做）

class Solution {
public:int reversePairs_helper(vector<int>& nums,int left,int right){if(left>=right) return 0;int ret=0;//1、找中間點，將數組分成兩部分int mid=(left+right)>>1;//2.左邊的個數+排序+右邊的個數+排序ret +=reversePairs_helper(nums,left,mid);ret +=reversePairs_helper(nums,mid+1,right);//3.一左一右的個數int cur1=left,cur2=mid+1,i=0;vector<int> tmp(right-left+2);while(cur1<=mid && cur2<=right){if(nums[cur1]<=nums[cur2]) tmp[i++]=nums[cur1++];else{ret+= mid-cur1+1;tmp[i++]=nums[cur2++];}}while(cur1<=mid) tmp[i++]=nums[cur1++];while(cur2<=right) tmp[i++]=nums[cur2++];for(int j=left;j<=right;j++)nums[j]=tmp[j-left];return ret;}int reversePairs(vector<int>& record) {return reversePairs_helper(record,0,record.size()-1);}
};

16.計算右側小於當前元素的個數

class Solution {vector<int> ret;vector<int> index;//記錄nums當前元素的下標、int tmpNums[500010];int tmpIndex[500010];
public:vector<int> countSmaller(vector<int>& nums) {int n=nums.size();ret.resize(n);index.resize(n);for(int i=0;i<n;i++)index[i]=i;mergesort(nums,0,nums.size()-1);return ret;}void mergesort(vector<int>& nums,int left,int right)  {if(left>=right) return;int mid=(left+right)>>1;mergesort(nums,left,mid);mergesort(nums,mid+1,right);int cur1=left,cur2=mid+1,i=0;while(cur1<=mid && cur2<=right){if(nums[cur1]>nums[cur2]){tmpNums[i]=nums[cur1];ret[index[cur1]]+=right-cur2+1;tmpIndex[i]=index[cur1];i++;cur1++;}else{tmpNums[i]=nums[cur2];tmpIndex[i]=index[cur2];i++;cur2++;}}while(cur1<=mid){tmpNums[i]=nums[cur1];tmpIndex[i]=index[cur1];i++;cur1++;}while(cur2<=right){tmpNums[i]=nums[cur2];tmpIndex[i]=index[cur2];i++;cur2++;}for(int j=left;j<=right;j++){nums[j]=tmpNums[j-left];index[j]=tmpIndex[j-left];}}
};

17.翻轉對