Python 機器學習 基礎 之 數據表示與特征工程 【單變量非線性變換 / 自動化特征選擇/利用專家知識】的簡單說明
目錄
Python 機器學習 基礎 之 數據表示與特征工程 【單變量非線性變換 / 自動化特征選擇/利用專家知識】的簡單說明
一、簡單介紹
二、單變量非線性變換
三、自動化特征選擇
四、利用專家知識
附錄
一、參考文獻
一、簡單介紹
Python是一種跨平臺的計算機程序設計語言。是一種面向對象的動態類型語言,最初被設計用于編寫自動化腳本(shell),隨著版本的不斷更新和語言新功能的添加,越多被用于獨立的、大型項目的開發。Python是一種解釋型腳本語言,可以應用于以下領域: Web 和 Internet開發、科學計算和統計、人工智能、教育、桌面界面開發、軟件開發、后端開發、網絡爬蟲。
Python 機器學習是利用 Python 編程語言中的各種工具和庫來實現機器學習算法和技術的過程。Python 是一種功能強大且易于學習和使用的編程語言,因此成為了機器學習領域的首選語言之一。Python 提供了豐富的機器學習庫,如Scikit-learn、TensorFlow、Keras、PyTorch等,這些庫包含了許多常用的機器學習算法和深度學習框架,使得開發者能夠快速實現、測試和部署各種機器學習模型。
Python 機器學習涵蓋了許多任務和技術,包括但不限于:
- 監督學習:包括分類、回歸等任務。
- 無監督學習:如聚類、降維等。
- 半監督學習:結合了有監督和無監督學習的技術。
- 強化學習:通過與環境的交互學習來優化決策策略。
- 深度學習:利用深度神經網絡進行學習和預測。
通過 Python 進行機器學習,開發者可以利用其豐富的工具和庫來處理數據、構建模型、評估模型性能,并將模型部署到實際應用中。Python 的易用性和龐大的社區支持使得機器學習在各個領域都得到了廣泛的應用和發展。
二、單變量非線性變換
在機器學習中的特征工程中,單變量非線性變換是一種將單個特征應用非線性函數的技術,以便提高模型性能或滿足模型假設。這些變換有助于處理特征與目標變量之間的非線性關系。常見的單變量非線性變換包括對數變換、平方根變換、平方變換、指數變換等。
下面是一些常用的單變量非線性變換的示例:
1)示例:對數變換
對數變換常用于將具有右偏分布的數據拉近正態分布。它在處理正數數據時特別有用。
import numpy as np import matplotlib.pyplot as plt from sklearn.datasets import fetch_california_housing from sklearn.model_selection import train_test_split# 加載加州房價數據集 california = fetch_california_housing() X_train, X_test, y_train, y_test = train_test_split(california.data, california.target, random_state=0)# 選擇一個特征進行對數變換 feature = X_train[:, 0] # 'MedInc' 特征 log_feature = np.log(feature + 1) # 加1以避免對數0的情況# 繪制原始特征和對數變換后的特征 plt.figure(figsize=(12, 6)) plt.subplot(1, 2, 1) plt.hist(feature, bins=30) plt.title("Original Feature") plt.subplot(1, 2, 2) plt.hist(log_feature, bins=30) plt.title("Log-transformed Feature") plt.show()2)示例:平方根變換
平方根變換用于減弱特征中較大的數值的影響。它在處理計數數據時特別有用。
sqrt_feature = np.sqrt(feature)# 繪制原始特征和平方根變換后的特征 plt.figure(figsize=(12, 6)) plt.subplot(1, 2, 1) plt.hist(feature, bins=30) plt.title("Original Feature") plt.subplot(1, 2, 2) plt.hist(sqrt_feature, bins=30) plt.title("Square-root-transformed Feature") plt.show()3)示例:平方變換
平方變換用于增加特征的非線性性。它在處理特征與目標之間具有二次關系的數據時有用。
square_feature = np.square(feature)# 繪制原始特征和平方變換后的特征 plt.figure(figsize=(12, 6)) plt.subplot(1, 2, 1) plt.hist(feature, bins=30) plt.title("Original Feature") plt.subplot(1, 2, 2) plt.hist(square_feature, bins=30) plt.title("Square-transformed Feature") plt.show()4)示例:指數變換
指數變換用于增強特征中較小的數值的影響。
exp_feature = np.exp(feature)# 繪制原始特征和指數變換后的特征 plt.figure(figsize=(12, 6)) plt.subplot(1, 2, 1) plt.hist(feature, bins=30) plt.title("Original Feature") plt.subplot(1, 2, 2) plt.hist(exp_feature, bins=30) plt.title("Exponential-transformed Feature") plt.show()5)將非線性變換應用到所有特征
如果你想對數據集中的所有特征進行非線性變換,可以使用
FunctionTransformer。from sklearn.preprocessing import FunctionTransformer# 定義對數變換的函數 log_transformer = FunctionTransformer(np.log1p, validate=True)# 應用對數變換到所有特征 X_train_log = log_transformer.transform(X_train) X_test_log = log_transformer.transform(X_test)print("Original shape:", X_train.shape) print("Log-transformed shape:", X_train_log.shape)這些非線性變換可以幫助捕捉特征和目標變量之間的復雜關系,從而提高模型的性能。選擇適當的變換方法取決于數據的分布和模型的需求。
添加特征的平方或立方可以改進線性回歸模型。其他變換通常也對變換某些特征有用,特別是應用數學函數,比如 log 、exp 或 sin 。雖然基于樹的模型只關注特征的順序,但線性模型和神經網絡依賴于每個特征的尺度和分布。如果在特征和目標之間存在非線性關系,那么建模就變得非常困難,特別是對于回歸問題。log 和 exp 函數可以幫助調節數據的相對比例,從而改進線性模型或神經網絡的學習效果。我們之前對內存價格數據應用過這種函數。在處理具有周期性模式的數據時,sin 和 cos 函數非常有用。
大部分模型都在每個特征(在回歸問題中還包括目標值)大致遵循高斯分布時表現最好,也就是說,每個特征的直方圖應該具有類似于熟悉的“鐘形曲線”的形狀。使用諸如 log 和 exp 之類的變換并不稀奇,但卻是實現這一點的簡單又有效的方法。在一種特別常見的情況下,這樣的變換非常有用,就是處理整數計數數據時。計數數據是指類似“用戶 A 多長時間登錄一次?”這樣的特征。計數不可能取負值,并且通常遵循特定的統計模式。下面我們使用一個模擬的計數數據集,其性質與在自然狀態下能找到的數據集類似。特征全都是整數值,而響應是連續的:
import numpy as nprnd = np.random.RandomState(0)
X_org = rnd.normal(size=(1000, 3))
w = rnd.normal(size=3)X = rnd.poisson(10 * np.exp(X_org))
y = np.dot(X_org, w)
我們來看一下第一個特征的前 10 個元素。它們都是正整數,但除此之外很難找出特定的模式。
如果我們計算每個值的出現次數,那么數值的分布將變得更清楚:
print("Number of feature appearances:\n{}".format(np.bincount(X[:, 0])))Number of feature appearances: [28 38 68 48 61 59 45 56 37 40 35 34 36 26 23 26 27 21 23 23 18 21 10 917 9 7 14 12 7 3 8 4 5 5 3 4 2 4 1 1 3 2 5 3 8 2 52 1 2 3 3 2 2 3 3 0 1 2 1 0 0 3 1 0 0 0 1 3 0 10 2 0 1 1 0 0 0 0 1 0 0 2 2 0 1 1 0 0 0 0 1 1 00 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 1 0 0 0 0 0 0 01 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1]
數字 2 似乎是最常見的,共出現了 68 次(bincount?始終從 0 開始),更大數字的出現次數快速下降。但也有一些很大的數字,比如 134 出現了 2 次 (這里 134 實際的出現次數是 0,但 84 和 85 的出現次數是 2,作者想要表達的意思是沒錯的) 。我們在圖 4-7 中將計數可視化。
bins = np.bincount(X[:, 0])
plt.bar(range(len(bins)), bins, color='b')
plt.ylabel("Number of appearances")
plt.xlabel("Value")plt.tight_layout()
plt.savefig('Images/04UnivariateNonlinearTransformation-01.png', bbox_inches='tight')
plt.show()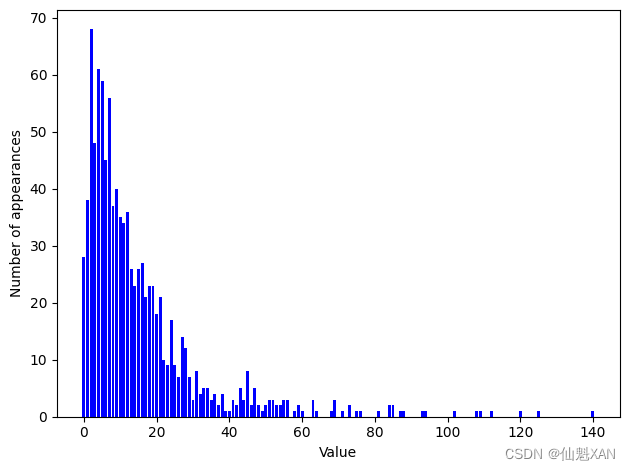
特征?X[:, 1]?和?X[:, 2]?具有類似的性質。這種類型的數值分布(許多較小的值和一些非常大的值)在實踐中非常常見(這是泊松分布,對計數數據相當重要)。 但大多數線性模型無法很好地處理這種數據。我們嘗試擬合一個嶺回歸模型:
from sklearn.linear_model import Ridge
from sklearn.model_selection import train_test_splitX_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
score = Ridge().fit(X_train, y_train).score(X_test, y_test)
print("Test score: {:.3f}".format(score))Test score: 0.622
你可以從相對較小的? 分數中看出,
Ridge?無法真正捕捉到?X?和?y?之間的關系。不過應用對數變換可能有用。由于數據取值中包括 0(對數在 0 處沒有定義),所以我們不能直接應用?log?,而是要計算?log(X + 1)?:
X_train_log = np.log(X_train + 1)
X_test_log = np.log(X_test + 1)
變換之后,數據分布的不對稱性變小,也不再有非常大的異常值(見圖 4-8):
plt.hist(X_train_log[:, 0], bins=25, color='b')
plt.ylabel("Number of appearances")
plt.xlabel("Value")plt.tight_layout()
plt.savefig('Images/04UnivariateNonlinearTransformation-02.png', bbox_inches='tight')
plt.show()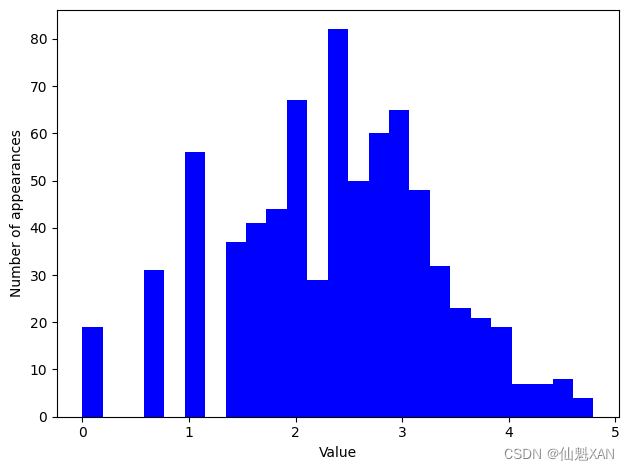
在新數據上構建一個嶺回歸模型,可以得到更好的擬合:
score = Ridge().fit(X_train_log, y_train).score(X_test_log, y_test)
print("Test score: {:.3f}".format(score))Test score: 0.875
為數據集和模型的所有組合尋找最佳變換,這在某種程度上是一門藝術。在這個例子中,所有特征都具有相同的性質,這在實踐中是非常少見的情況。通常來說,只有一部分特征應該進行變換,有時每個特征的變換方式也各不相同。前面提到過,對基于樹的模型而言,這種變換并不重要,但對線性模型來說可能至關重要。對回歸的目標變量?y?進行變換有時也是一個好主意。嘗試預測計數(比如訂單數量)是一項相當常見的任務,而且使用?log(y + 1)?變換也往往有用。(這是對泊松分布非常粗略的近似,而從概率的角度來看,這是正確的解決方法)
從前面的例子中可以看出,分箱、多項式和交互項都對模型在給定數據集上的性能有很大影響,對于復雜度較低的模型更是這樣,比如線性模型和樸素貝葉斯模型。與之相反,基于樹的模型通常能夠自己發現重要的交互項,大多數情況下不需要顯式地變換數據。其他模型,比如 SVM、最近鄰和神經網絡,有時可能會從使用分箱、交互項或多項式中受益,但其效果通常不如線性模型那么明顯。
三、自動化特征選擇
自動化特征選擇是機器學習中用于提高模型性能和減少模型復雜性的重要步驟。通過自動化特征選擇,我們可以選擇對模型預測有顯著影響的特征,去除冗余或不相關的特征,從而提高模型的泛化能力和訓練效率。
有了這么多種創建新特征的方法,你可能會想要增大數據的維度,使其遠大于原始特征的數量。但是,添加更多特征會使所有模型變得更加復雜,從而增大過擬合的可能性。在添加新特征或處理一般的高維數據集時,最好將特征的數量減少到只包含最有用的那些特征,并刪除其余特征。這樣會得到泛化能力更好、更簡單的模型。但你如何判斷每個特征的作用有多大呢?有三種基本的策略:單變量統計 (univariate statistics)、基于模型的選擇 (model-based selection)和迭代選擇 (iterative selection)。我們將詳細討論這三種策略。所有這些方法都是監督方法,即它們需要目標值來擬合模型。這也就是說,我們需要將數據劃分為訓練集和測試集,并只在訓練集上擬合特征選擇。
1、單變量統計
在單變量統計中,我們計算每個特征和目標值之間的關系是否存在統計顯著性,然后選擇具有最高置信度的特征。對于分類問題,這也被稱為方差分析?(analysis of variance,ANOVA)。這些測試的一個關鍵性質就是它們是單變量的?(univariate),即它們只單獨考慮每個特征。因此,如果一個特征只有在與另一個特征合并時才具有信息量,那么這個特征將被舍棄。單變量測試的計算速度通常很快,并且不需要構建模型。另一方面,它們完全獨立于你可能想要在特征選擇之后應用的模型。
想要在?scikit-learn?中使用單變量特征選擇,你需要選擇一項測試——對分類問題通常是?f_classif?(默認值),對回歸問題通常是?f_regression?——然后基于測試中確定的?p?值來選擇一種舍棄特征的方法。所有舍棄參數的方法都使用閾值來舍棄所有?p?值過大的特征(意味著它們不可能與目標值相關)。計算閾值的方法各有不同,最簡單的是?SelectKBest?和?SelectPercentile?,前者選擇固定數量的 k 個特征,后者選擇固定百分比的特征。我們將分類的特征選擇應用于?cancer?數據集。為了使任務更難一點,我們將向數據中添加一些沒有信息量的噪聲特征。我們期望特征選擇能能夠識別沒有信息量的特征并刪除它們:
from sklearn.datasets import load_breast_cancer
from sklearn.feature_selection import SelectPercentile
from sklearn.model_selection import train_test_split
import numpy as npcancer = load_breast_cancer()# 獲得確定性的隨機數
rng = np.random.RandomState(42)
noise = rng.normal(size=(len(cancer.data), 50))
# 向數據中添加噪聲特征
# 前30個特征來自數據集,后50個是噪聲
X_w_noise = np.hstack([cancer.data, noise])X_train, X_test, y_train, y_test = train_test_split(X_w_noise, cancer.target, random_state=0, test_size=.5)
# 使用f_classif(默認值)和SelectPercentile來選擇50%的特征
select = SelectPercentile(percentile=50)
select.fit(X_train, y_train)
# 對訓練集進行變換
X_train_selected = select.transform(X_train)print("X_train.shape: {}".format(X_train.shape))
print("X_train_selected.shape: {}".format(X_train_selected.shape))X_train.shape: (284, 80) X_train_selected.shape: (284, 40)
如你所見,特征的數量從 80 減少到 40(原始特征數量的 50%)。我們可以用?get_support?方法來查看哪些特征被選中,它會返回所選特征的布爾遮罩(mask)(其可視化見圖 4-9):
import matplotlib.pyplot as pltmask = select.get_support()
print(mask)
# 將遮罩可視化——黑色為True,白色為False
plt.matshow(mask.reshape(1, -1), cmap='gray_r')
plt.xlabel("Sample index")plt.tight_layout()
plt.savefig('Images/05AutomatedFeatureSelection-01.png', bbox_inches='tight')
plt.show()[ True True True True True True True True True False True FalseTrue True True True True True False False True True True TrueTrue True True True True True False False False True False TrueFalse False True False False False False True False False True FalseFalse True False True False False False False False False True FalseTrue False False False False True False True False False False FalseTrue True False True False False False False]

你可以從遮罩的可視化中看出,大多數所選擇的特征都是原始特征,并且大多數噪聲特征都已被刪除。但原始特征的還原并不完美。我們來比較 Logistic 回歸在所有特征上的性能與僅使用所選特征的性能:
from sklearn.linear_model import LogisticRegression# 對測試數據進行變換
X_test_selected = select.transform(X_test)lr = LogisticRegression()
lr.fit(X_train, y_train)
print("Score with all features: {:.3f}".format(lr.score(X_test, y_test)))
lr.fit(X_train_selected, y_train)
print("Score with only selected features: {:.3f}".format(lr.score(X_test_selected, y_test)))在這個例子中,刪除噪聲特征可以提高性能,即使丟失了某些原始特征。這是一個非常簡單的假想示例,在真實數據上的結果要更加復雜。不過,如果特征量太大以至于無法構建模型,或者你懷疑許多特征完全沒有信息量,那么單變量特征選擇還是非常有用的。
Score with all features: 0.919 Score with only selected features: 0.919
2、基于模型的特征選擇
基于模型的特征選擇使用一個監督機器學習模型來判斷每個特征的重要性,并且僅保留最重要的特征。用于特征選擇的監督模型不需要與用于最終監督建模的模型相同。特征選擇模型需要為每個特征提供某種重要性度量,以便用這個度量對特征進行排序。決策樹和基于決策樹的模型提供了?feature_importances_ 屬性,可以直接編碼每個特征的重要性。線性模型系數的絕對值也可以用于表示特征重要性。正如我們在之前所見,L1 懲罰的線性模型學到的是稀疏系數,它只用到了特征的一個很小的子集。這可以被視為模型本身的一種特征選擇形式,但也可以用作另一個模型選擇特征的預處理步驟。與單變量選擇不同,基于模型的選擇同時考慮所有特征,因此可以獲取交互項(如果模型能夠獲取它們的話)。要想使用基于模型的特征選擇,我們需要使用?SelectFromModel?變換器:
from sklearn.feature_selection import SelectFromModel
from sklearn.ensemble import RandomForestClassifier
select = SelectFromModel(RandomForestClassifier(n_estimators=100, random_state=42),threshold="median")SelectFromModel?類選出重要性度量(由監督模型提供)大于給定閾值的所有特征。為了得到可以與單變量特征選擇進行對比的結果,我們使用中位數作為閾值,這樣就可以選擇一半特征。我們用包含 100 棵樹的隨機森林分類器來計算特征重要性。這是一個相當復雜的模型,也比單變量測試要強大得多。下面我們來實際擬合模型:
select.fit(X_train, y_train)
X_train_l1 = select.transform(X_train)
print("X_train.shape: {}".format(X_train.shape))
print("X_train_l1.shape: {}".format(X_train_l1.shape))X_train.shape: (284, 80) X_train_l1.shape: (284, 40)
我們可以再次查看選中的特征(見圖 4-10):
mask = select.get_support()
# 將遮罩可視化——黑色為True,白色為False
plt.matshow(mask.reshape(1, -1), cmap='gray_r')
plt.xlabel("Sample index")plt.tight_layout()
plt.savefig('Images/05AutomatedFeatureSelection-02.png', bbox_inches='tight')
plt.show()
這次,除了兩個原始特征,其他原始特征都被選中。由于我們指定選擇 40 個特征,所以也選擇了一些噪聲特征。我們來看一下其性能:
X_test_l1 = select.transform(X_test)
score = LogisticRegression().fit(X_train_l1, y_train).score(X_test_l1, y_test)
print("Test score: {:.3f}".format(score))Test score: 0.930
利用更好的特征選擇,性能也得到了提高。
3、迭代特征選擇
在單變量測試中,我們沒有使用模型,而在基于模型的選擇中,我們使用了單個模型來選擇特征。在迭代特征選擇中,將會構建一系列模型,每個模型都使用不同數量的特征。有兩種基本方法:開始時沒有特征,然后逐個添加特征,直到滿足某個終止條件;或者從所有特征開始,然后逐個刪除特征,直到滿足某個終止條件。由于構建了一系列模型,所以這些方法的計算成本要比前面討論過的方法更高。其中一種特殊方法是遞歸特征消除?(recursive feature elimination,RFE),它從所有特征開始構建模型,并根據模型舍棄最不重要的特征,然后使用除被舍棄特征之外的所有特征來構建一個新模型,如此繼續,直到僅剩下預設數量的特征。為了讓這種方法能夠運行,用于選擇的模型需要提供某種確定特征重要性的方法,正如基于模型的選擇所做的那樣。下面我們使用之前用過的同一個隨機森林模型,得到的結果如圖 4-11 所示:
from sklearn.feature_selection import RFE
select = RFE(RandomForestClassifier(n_estimators=100, random_state=42),n_features_to_select=40)
select.fit(X_train, y_train)
# 將選中的特征可視化:
mask = select.get_support()
plt.matshow(mask.reshape(1, -1), cmap='gray_r')
plt.xlabel("Sample index")plt.tight_layout()
plt.savefig('Images/05AutomatedFeatureSelection-03.png', bbox_inches='tight')
plt.show()
與單變量選擇和基于模型的選擇相比,迭代特征選擇的結果更好,但仍然漏掉了一個特征。運行上述代碼需要的時間也比基于模型的選擇長得多,因為對一個隨機森林模型訓練了 40 次,每運行一次刪除一個特征。我們來測試一下使用 RFE 做特征選擇時 Logistic 回歸模型的精度:
X_train_rfe= select.transform(X_train)
X_test_rfe= select.transform(X_test)score = LogisticRegression().fit(X_train_rfe, y_train).score(X_test_rfe, y_test)
print("Test score: {:.3f}".format(score))Test score: 0.930
我們還可以利用在 RFE 內使用的模型來進行預測。這僅使用被選中的特征集:
print("Test score: {:.3f}".format(select.score(X_test, y_test)))Test score: 0.951
這里,在 RFE 內部使用的隨機森林的性能,與在所選特征上訓練一個 Logistic 回歸模型得到的性能相同。換句話說,只要我們選擇了正確的特征,線性模型的表現就與隨機森林一樣好。
如果你不確定何時選擇使用哪些特征作為機器學習算法的輸入,那么自動化特征選擇可能特別有用。它還有助于減少所需要的特征數量,加快預測速度,或允許可解釋性更強的模型。在大多數現實情況下,使用特征選擇不太可能大幅提升性能,但它仍是特征工程工具箱中一個非常有價值的工具。
四、利用專家知識
對于特定應用來說,在特征工程中通常可以利用專家知識 (expert knowledge)。雖然在許多情況下,機器學習的目的是避免創建一組專家設計的規則,但這并不意味著應該舍棄該應用或該領域的先驗知識。通常來說,領域專家可以幫助找出有用的特征,其信息量比數據原始表示要大得多。想象一下,你在一家旅行社工作,想要預測機票價格。假設你有價格以及日期、航空公司、出發地和目的地的記錄。機器學習模型可能從這些記錄中構建一個相當不錯的模型,但可能無法學到機票價格中的某些重要因素。例如,在度假高峰月份和假日期間,機票價格通常更高。雖然某些假日的日期是固定的(比如圣誕節),其影響可以從日期中學到,但其他假日的日期可能取決于月相(比如光明節和復活節),或者由官方規定(比如學校放假)。如果每個航班都只使用公歷記錄日期,則無法從數據中學到這些事件。但添加一個特征是很簡單的,其中編碼了一個航班在公休假日或學校假期的之前、之中還是之后。利用這種方法可以將關于任務屬性的先驗知識編碼到特征中,以輔助機器學習算法。添加一個特征并不會強制機器學習算法使用它,即使最終發現假日信息不包含關于機票價格的信息,用這一信息來擴充數據也不會有什么害處。
下面我們來看一個利用專家知識的特例——雖然在這個例子中,對這些專家知識更正確的叫法應該是“常識”。任務是預測在 Andreas 家門口的自行車出租。
在紐約,Citi Bike 運營著一個帶有付費系統的自行車租賃站網絡。這些站點遍布整個城市,提供了一種方便的交通方式。自行車出租數據以匿名形式公開(Citi Bike System Data | Citi Bike NYC ),并用各種方法進行了分析。我們想要解決的任務是,對于給定的日期和時間,預測有多少人將會在 Andreas 的家門口租一輛自行車——這樣他就知道是否還有自行車留給他。
我們首先將這個站點 2015 年 8 月的數據加載為一個?pandas?數據框。我們將數據重新采樣為每 3 小時一個數據,以得到每一天的主要趨勢:
import mglearncitibike = mglearn.datasets.load_citibike()
print("Citi Bike data:\n{}".format(citibike.head()))Citi Bike data: starttime 2015-08-01 00:00:00 3 2015-08-01 03:00:00 0 2015-08-01 06:00:00 9 2015-08-01 09:00:00 41 2015-08-01 12:00:00 39 Freq: 3h, Name: one, dtype: int64
下面這個示例給出了整個月租車數量的可視化(圖 4-12):
import pandas as pdplt.figure(figsize=(10, 3))
xticks = pd.date_range(start=citibike.index.min(), end=citibike.index.max(),freq='D')
plt.xticks(xticks, xticks.strftime("%a %m-%d"), rotation=90, ha="left")
plt.plot(citibike, linewidth=1)
plt.xlabel("Date")
plt.ylabel("Rentals")plt.tight_layout()
plt.savefig('Images/05AutomatedFeatureSelection-04.png', bbox_inches='tight')
plt.show()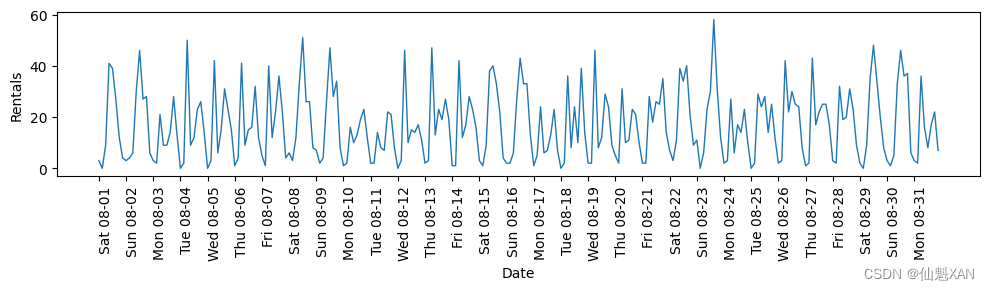
觀察此數據,我們可以清楚地區分每 24 小時中的白天和夜間。工作日和周末的模式似乎也有很大不同。在對這種時間序列上的預測任務進行評估時,我們通常希望從過去學習?并預測未來?。也就是說,在劃分訓練集和測試集的時候,我們希望使用某個特定日期之前的所有數據作為訓練集,該日期之后的所有數據作為測試集。這是我們通常使用時間序列預測的方式:已知過去所有的出租數據,我們認為明天會發生什么?我們將使用前 184 個數據點(對應前 23 天)作為訓練集,剩余的 64 個數據點(對應剩余的 8 天)作為測試集。
在我們的預測任務中,我們使用的唯一特征就是某一租車數量對應的日期和時間。因此輸入特征是日期和時間,比如?2015-08-01 00:00:00?,而輸出是在接下來 3 小時內的租車數量(根據我們的?DataFrame?,在這個例子中是 3)。
在計算機上存儲日期的常用方式是使用 POSIX 時間(這有些令人意外),它是從 1970 年 1 月 1 日 00:00:00(也就是 Unix 時間的起點)起至現在的總秒數。首先,我們可以嘗試使用這個單一整數特征作為數據表示:
# 提取目標值(租車數量)
y = citibike.values# 將時間轉換為 POSIX 時間(即時間戳)
X = citibike.index
X = pd.to_datetime(X) # 確保索引是日期時間格式
X = X.view('int64') // 10**9 # 轉換為秒時間戳并轉換為整數# 轉換為二維數組
X = X.reshape(-1, 1)print(X[:5])
print(y[:5])我們首先定義一個函數,它可以將數據劃分為訓練集和測試集,構建模型并將結果可視化:
# 使用前184個數據點用于訓練,剩余的數據點用于測試
n_train = 184# 對給定特征集上的回歸進行評估和作圖的函數
def eval_on_features(features, target, regressor):# 將給定特征劃分為訓練集和測試集X_train, X_test = features[:n_train], features[n_train:]# 同樣劃分目標數組y_train, y_test = target[:n_train], target[n_train:]regressor.fit(X_train, y_train)print("Test-set R^2: {:.2f}".format(regressor.score(X_test, y_test)))y_pred = regressor.predict(X_test)y_pred_train = regressor.predict(X_train)plt.figure(figsize=(10, 3))plt.xticks(range(0, len(X), 8), xticks.strftime("%a %m-%d"), rotation=90,ha="left")plt.plot(range(n_train), y_train, label="train")plt.plot(range(n_train, len(y_test) + n_train), y_test, '-', label="test")plt.plot(range(n_train), y_pred_train, '--', label="prediction train")plt.plot(range(n_train, len(y_test) + n_train), y_pred, '--',label="prediction test")plt.legend(loc=(1.01, 0))plt.xlabel("Date")plt.ylabel("Rentals")我們之前看到,隨機森林需要很少的數據預處理,因此它似乎很適合作為第一個模型。我們使用 POSIX 時間特征?X?,并將隨機森林回歸傳入我們的?eval_on_features?函數。結果如圖 4-13 所示。
from sklearn.ensemble import RandomForestRegressor
regressor = RandomForestRegressor(n_estimators=100, random_state=0)
plt.figure()
eval_on_features(X, y, regressor)plt.tight_layout()
plt.savefig('Images/05AutomatedFeatureSelection-05.png', bbox_inches='tight')
plt.show()Test-set R^2: -0.04
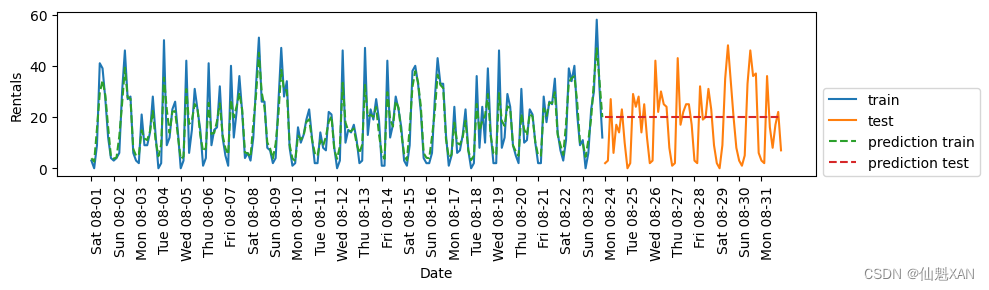
在訓練集上的預測結果相當好,這符合隨機森林通常的表現。但對于測試集來說,預測結果是一條常數直線。R2?為 -0.04,說明我們什么都沒有學到。發生了什么?
問題在于特征和隨機森林的組合。測試集中 POSIX 時間特征的值超出了訓練集中特征取值的范圍:測試集中數據點的時間戳要晚于訓練集中的所有數據點。樹以及隨機森林無法外推?(extrapolate)到訓練集之外的特征范圍。結果就是模型只能預測訓練集中最近數據點的目標值,即最后一次觀測到數據的時間。
顯然,我們可以做得更好。這就是我們的“專家知識”的用武之地。通過觀察訓練數據中的租車數量圖像,我們發現兩個因素似乎非常重要:一天內的時間與一周的星期幾。因此我們來添加這兩個特征。我們從 POSIX 時間中學不到任何東西,所以刪掉這個特征。首先,我們僅使用每天的時刻。如圖 4-14 所示,現在的預測結果對一周內的每天都具有相同的模式:
# 獲取小時信息并轉換為二維數組
X_hour = citibike.index.hour.to_numpy().reshape(-1, 1)
eval_on_features(X_hour, y, regressor)plt.tight_layout()
plt.savefig('Images/05AutomatedFeatureSelection-06.png', bbox_inches='tight')
plt.show()Test-set R^2: 0.60
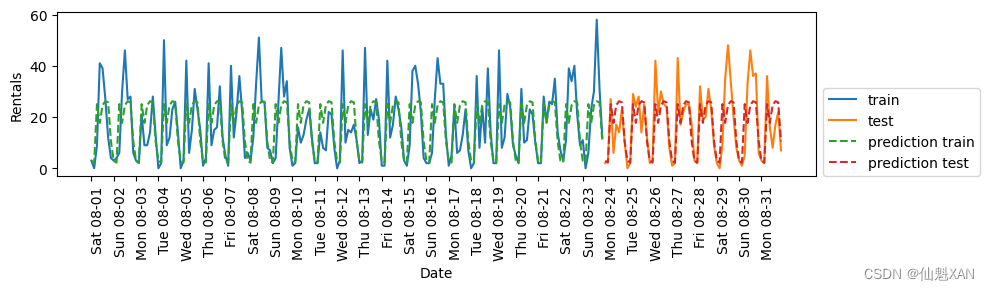
已經好多了,但預測結果顯然沒有抓住每周的模式。下面我們還添加一周的星期幾作為特征(見圖 4-15):
X_hour_week = np.hstack([citibike.index.dayofweek.to_numpy().reshape(-1, 1),citibike.index.hour.to_numpy().reshape(-1, 1)])
eval_on_features(X_hour_week, y, regressor)plt.tight_layout()
plt.savefig('Images/05AutomatedFeatureSelection-07.png', bbox_inches='tight')
plt.show()Test-set R^2: 0.84
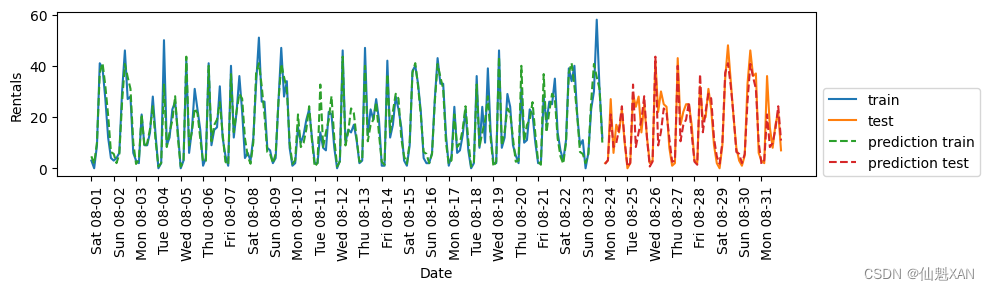
現在我們的模型通過考慮一周的星期幾和一天內的時間捕捉到了周期性的行為。它的 R2?為 0.84,預測性能相當好。模型學到的內容可能是 8 月前 23 天中星期幾與時刻每種組合的平均租車數量。這實際上不需要像隨機森林這樣復雜的模型,所以我們嘗試一個更簡單的模型——LinearRegression?(見圖 4-16):
from sklearn.linear_model import LinearRegression
eval_on_features(X_hour_week, y, LinearRegression())plt.tight_layout()
plt.savefig('Images/05AutomatedFeatureSelection-08.png', bbox_inches='tight')
plt.show()Test-set R^2: 0.13
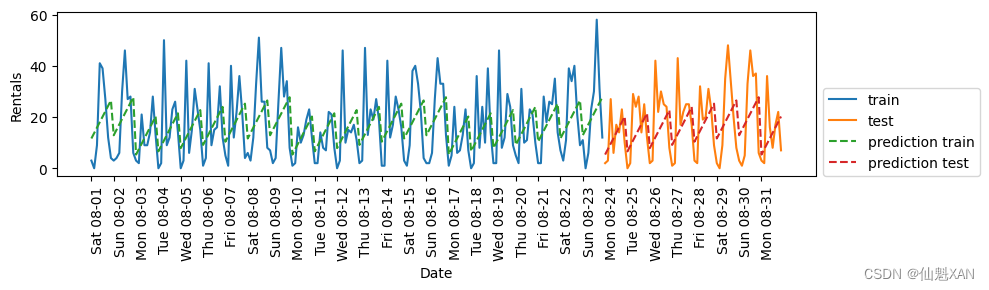
LinearRegression 的效果差得多,而且周期性模式看起來很奇怪。其原因在于我們用整數編碼一周的星期幾和一天內的時間,它們被解釋為連續變量。因此,線性模型只能學到關于每天時間的線性函數——它學到的是,時間越晚,租車數量越多。但實際模式比這要復雜得多。我們可以通過將整數解釋為分類變量(用 OneHotEncoder 進行變換)來獲取這種模式(見圖 4-17):
from sklearn.preprocessing import OneHotEncoder
from sklearn.linear_model import Ridgeenc = OneHotEncoder()
X_hour_week_onehot = enc.fit_transform(X_hour_week).toarray()eval_on_features(X_hour_week_onehot, y, Ridge())plt.tight_layout()
plt.savefig('Images/05AutomatedFeatureSelection-09.png', bbox_inches='tight')
plt.show()Test-set R^2: 0.62

它給出了比連續特征編碼好得多的匹配。現在線性模型為一周內的每天都學到了一個系數,為一天內的每個時刻都學到了一個系數。也就是說,一周七天共享“一天內每個時刻”的模式。
利用交互特征,我們可以讓模型為星期幾和時刻的每一種組合學到一個系數(見圖 4-18):
from sklearn.preprocessing import PolynomialFeaturespoly_transformer = PolynomialFeatures(degree=2, interaction_only=True,include_bias=False)
X_hour_week_onehot_poly = poly_transformer.fit_transform(X_hour_week_onehot)
lr = Ridge()
eval_on_features(X_hour_week_onehot_poly, y, lr)plt.tight_layout()
plt.savefig('Images/05AutomatedFeatureSelection-10.png', bbox_inches='tight')
plt.show()Test-set R^2: 0.85
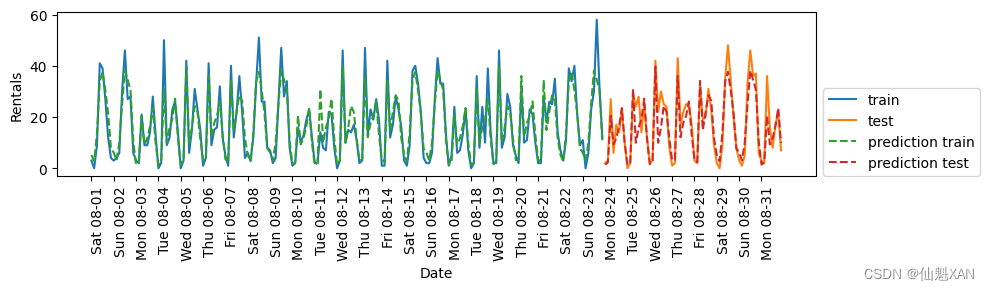
這一變換最終得到一個性能與隨機森林類似的模型。這個模型的一大優點是,可以很清楚地看到學到的內容:對每個星期幾和時刻的交互項學到了一個系數。我們可以將模型學到的系數作圖,而這對于隨機森林來說是不可能的。
首先,為時刻和星期幾特征創建特征名稱:
hour = ["%02d:00" % i for i in range(0, 24, 3)]
day = ["Mon", "Tue", "Wed", "Thu", "Fri", "Sat", "Sun"]
features = day + hour然后,利用?get_feature_names?方法對?PolynomialFeatures?提取的所有交互特征進行命名,并僅保留系數不為零的那些特征:
features_poly = poly_transformer.get_feature_names_out(features)
features_nonzero = np.array(features_poly)[lr.coef_ != 0]
coef_nonzero = lr.coef_[lr.coef_ != 0]下面將線性模型學到的系數可視化,如圖 4-19 所示:
plt.figure(figsize=(15, 2))
plt.plot(coef_nonzero, 'o')
plt.xticks(np.arange(len(coef_nonzero)), features_nonzero, rotation=90)
plt.xlabel("Feature name")
plt.ylabel("Feature magnitude")plt.tight_layout()
plt.savefig('Images/05AutomatedFeatureSelection-11.png', bbox_inches='tight')
plt.show()
附錄
一、參考文獻
參考文獻:[德] Andreas C. Müller [美] Sarah Guido 《Python Machine Learning Basics Tutorial》

:數據庫技術基礎)



)









)


