(1)單源點最短路徑問題
問題描述:
給定一個圖,任取其中一個節點為固定的起點,求從起點到任意節點的最短路徑距離。
例如: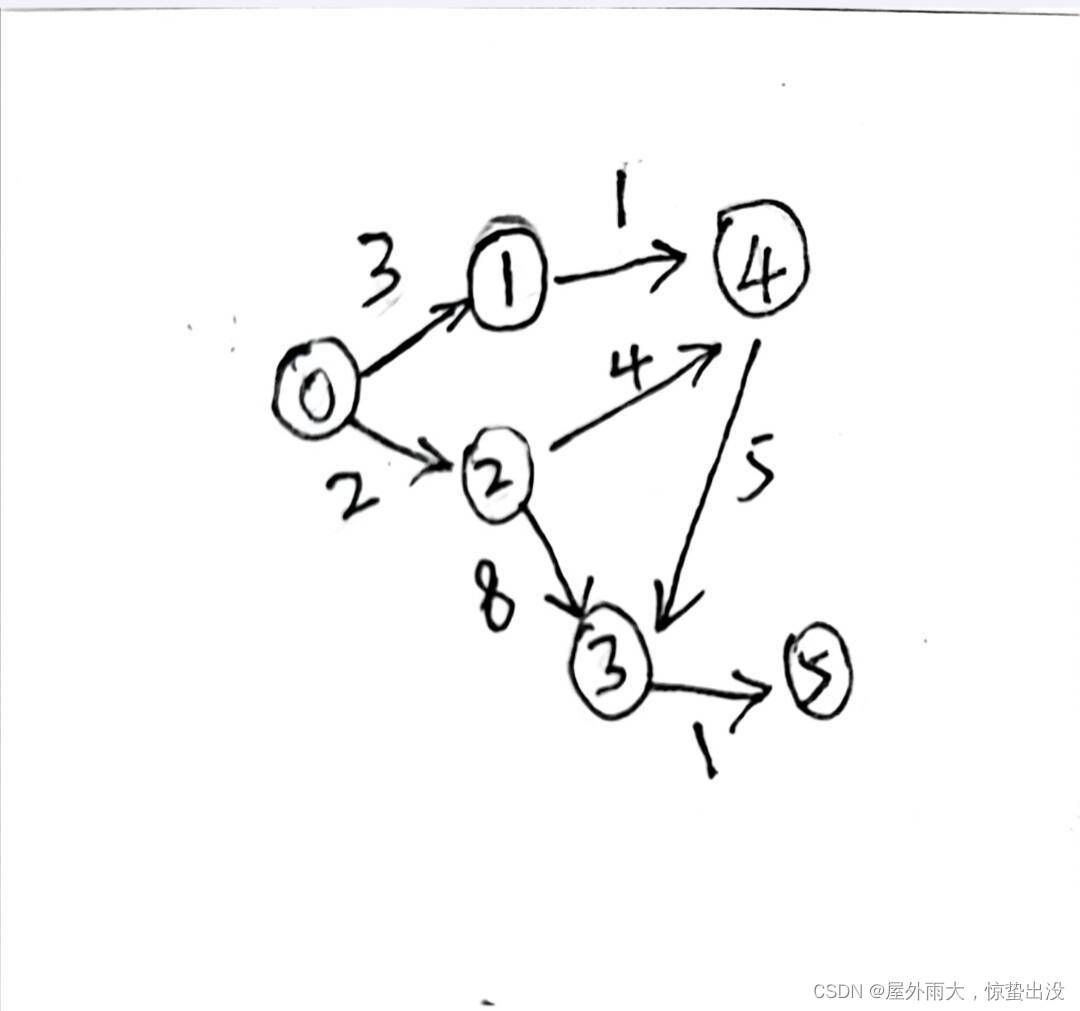
思路與關鍵點:
以下代碼中涉及到宏INT_MAX,存在于<limits.h>中。

首先,建立三個數組dist,S,W,prev分別用來存儲從起始節點到任意節點的最短距離;相對于s距離起點的最短路徑節點集合;存儲要遍歷的圖的各條邊的距離;用來存儲各個節點的直接前驅節點。
3個主要的個功能函數。
(1)minDistance函數用來尋找V-S集合中的距離起點的最短距離,并返回該節點的下標。
(2)dijkstra函數用來尋找從起始節點到任意節點的最短路徑長度。
思路是把節點分為兩類,一類是沒有放進S集合中的節點,一類是已經放進去的節點。那么,尋找從起始節點到節點v的最短路徑就有兩種可能的取值。
第一種是組成該最短路徑的就是dist[v]。
第二種是新加入S集合的節點u可能會組成一個新的更短的路徑,這時,要更新dist[v]。
(3)Traceback函數用來打印從源點到終點的路徑。這個函數基于prev數組,該數組建立的核心原理是:每次更新dist數組,一定是因為s集合中增加了一個節點u,這個u一定是當前更新dist[v]的直接前驅節點。遞歸調用,不斷找前一個前驅節點,就可以打印出完整路徑了。
偽代碼:

代碼:
#include <iostream>
#include <limits.h>using namespace std;
#define V 6 // 節點的數量void Traceback(int v, int i, int prev[]);int minDistance(int dist[], int S[]);void printSolution(int dist[]);void dijkstra(int W[V][V], int src);int main() {int W[V][V] = {{0, 3, 2, 0, 0, 0},{0, 0, 0, 0, 1, 0},{0, 0, 0, 8, 4, 0},{0, 0, 0, 0, 0, 1},{0, 0, 0, 5, 0, 0},{0, 0, 0, 0, 0, 0}};dijkstra(W, 0);//起始節點為節點 0 return 0;}
// 找到距離數組中最小值的索引
int minDistance(int dist[], int S[]) {int min = INT_MAX, min_index;for (int j = 0; j < V; j++) {/*如果節點j沒有包含在最短路徑數組中,初始時,只要有路徑,就更新最短路徑數組的值。后面,每次進入循環都與當前的最短距離進行比較,更新。找到V(全部節點集合)-S(已找到的最短路徑節點集合)中距離起點最短的路徑的節點編號。 */ if (S[j] == 0 && dist[j] <= min) {min = dist[j];min_index = j;}}return min_index;
}// 打印最終的最短路徑
void printSolution(int dist[]) {printf("節點\t最短距離\n");for (int i = 0; i < V; i++)printf("%d\t%d\n", i, dist[i]);
}// Dijkstra算法的實現
void dijkstra(int W[V][V], int src) {int dist[V]; // 存儲從源節點到每個節點的最短距離int S[V]; // 記錄節點是否已經包含在已找到的最短路徑節點集合中int prev[V];// 初始化所有距離為無窮大,標記所有節點為未包含for (int i = 0; i < V; i++) {dist[i] = INT_MAX;S[i] = 0;}// 設置起始節點的距離為0dist[src] = 0;// 找到最短路徑for (int count = 0; count < V - 1; count++) {// 選擇距離最小的節點int u = minDistance(dist, S);// 標記節點為已包含S[u] = 1;// 更新相鄰節點的距離for (int v = 0; v < V; v++) {/*如果該節點沒有包含在最短路徑數組中,有路徑可直接到達該節點,并且有路徑可達該節點,并且,從節點0到節點u的最短路徑長度,與,從節點u到節點v的路徑距離之和小于從節點0到該節點當前最短距離,則更新最短距離。 */ if (!S[v] &&W[u][v] && dist[u] != INT_MAX &&dist[u] +W[u][v] < dist[v]) {dist[v] = dist[u] + W[u][v];prev[v]=u;}}}// 打印最終的最短路徑printSolution(dist);int v,i;printf("請輸入源點及終點");cin>>v>>i;printf("從源點%d到終點%d的最短路徑為:\n",v,i);Traceback(v,i,prev);
}
//輸出最短路徑 v源點,i終點,
void Traceback(int v, int i, int prev[])
{// 源點等于終點時,即找出全部路徑if (v == i){cout << i;return;}Traceback(v, prev[i], prev);cout << "->" << i;
}運行結果:
關鍵步驟證明:
時間復雜度與空間復雜度:
時間復雜度為0(
),空間復雜度為0(
)。
(2)活動選擇問題
問題描述:
假定有一個n個活動的集合S={a1,a2,……,an},這些活動使用同一個資源,而這個資源在某個時刻只能供一個活動使用。每個活動有一個開始時間si和一個結束時間fi,其中0<=si<fi<∞。如果被選中,任務ai發生在半開時間區間[si,fi)期間。如果兩個活動ai和aj滿足[si,fi)和[sj,fj)不重疊,則稱他們是兼容的.也就是說,若si>=fj或sj>=fi,則ai和aj是兼容的。
在活動選擇問題中,我們希望選出一個最大兼容活動集。
例子: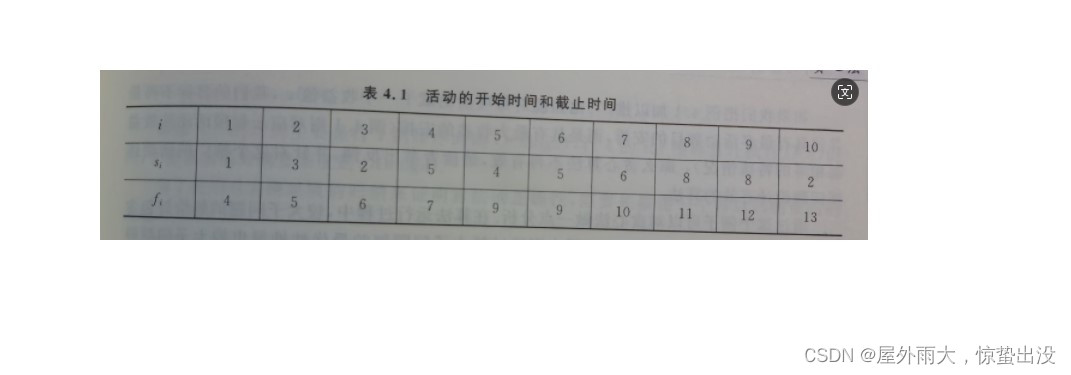
該活動序列的最大兼容活動集為1,4,8或1,4,9
思路與關鍵點:
按活動結束時間從小到大排序
每次選擇的活動將作為是否與下一個活動兼容的判斷依據。
偽代碼:

代碼:
#include<iostream>
#include<string.h>
using namespace std;
void Traceback(int Trace[],int n);
void sort(int n,int *s,int* f)
{int a,b,i,j;//冒泡排序,按結束時間從小到大排列活動 for(i=1;i<n;i++){for(j=1;j<n-i+1;j++){if(f[j]>f[j+1]){a=f[j];f[j]=f[j+1];f[j+1]=a;b=s[j];s[j]=s[j+1];s[j+1]=b;}}}
}
int GreedySelect(int n,int s[],int f[],bool A[])
{int Trace[n];Trace[1]=1;A[1]=true;//第一個活動必然在最優解中 int j=1,count=1; //從第二個活動開始,尋找下一個兼容的活動 for(int i=2;i<=n;i++){if(s[i]>=f[j]){A[i]=true;j=i;//將已經選人的最后一個活動標號作為下一次比較兼容的參照 count++;Trace[count]=i;}else A[i]=false;} Traceback(Trace,count);return count;
}
//打印的活動序列是按照結束時間從小到大排好序的活動序列,而不是原來的活動序列 void Traceback(int Trace[],int n){printf("活動安排順序為:");for(int i=1;i<=n;i++){cout<<"->"<<Trace[i];}cout<<endl;}
int main(){int n,s[50],f[50];bool A[50];memset(A,false,sizeof(A)); printf("請輸入活動個數:\n"); cin>>n;//活動標號與數組下標保持一致,從1開始標號 for(int i=1;i<=n;i++){printf("請輸入第%d個活動的開始時間和結束時間\n",i);cin>>s[i]>>f[i];printf("第%d個活動的開始時間是%d,結束時間是%d\n",i,s[i],f[i]);} sort(n,s,f);printf("最多相容活動數為:\n");cout<<GreedySelect(n,s,f,A)<<endl;return 0;
}運行結果:
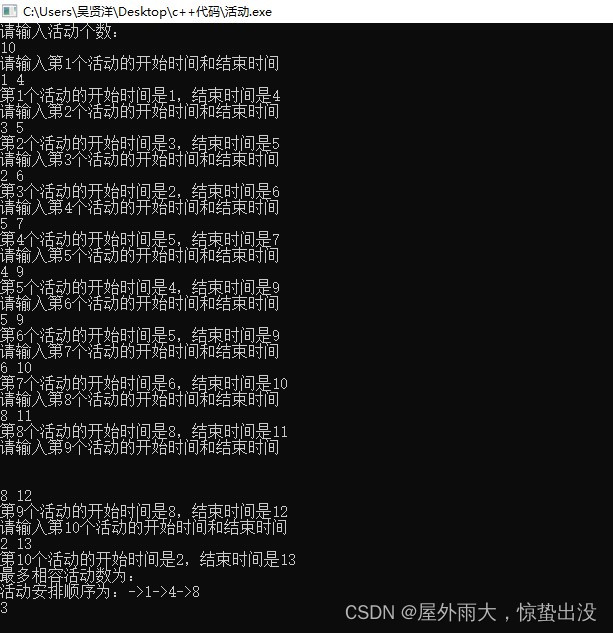
關鍵步驟證明:

時間復雜度與空間復雜度:
時間復雜度主要為排序花的時間為0(
),如果換成其他排序可以降低時間復雜度,空間復雜度為0(n)
(3)最小生成樹--prim算法實現
問題描述:
給定一個圖,求出其最小生成樹
最小生成樹定義
? ? 對于一個帶權(假定每條邊上的權值均為大于零的實數)連通無向圖G中的不同生成樹,各樹的邊上的權值之和可能不同;圖中所有生成樹中具有邊上的權值之和最小的樹稱為該圖的最小生成樹.? ? 按照生成樹的定義,n個頂點的連通圖的生成樹有n個頂點和(n-1)條邊.因此構造最小生成樹的準則有三條:
(1) 必須只使用該圖中的邊來構造最小生成樹;
(2) 必須使用且僅使用(n-1)條邊來連接圖中的n個頂點;
(3) 不能使用產生回路的邊.
思路與關鍵點:
首先,這里有一個頭文件<alogrithmn>,里面包含了豐富實用的函數,非常nice。這里使用到了其中的fill函數和min函數。分別用來填充數組和求最小值的。建立一個數組used,記錄哪些沒有進入最小生成樹的集合,每次不斷地將沒有加入used中的距離加入used數組的節點?權值最小的節點加入used數組。?更新V輪mincost數組,得到最小生成樹。
偽代碼:

代碼:
#include<iostream>
#include<algorithm>
#define MAX_V 100
#define INF 1000
using namespace std; int main()
{int V,E;int i,j,m,n;int cost[MAX_V][MAX_V];//存儲每個節點之間的權值 int mincost[MAX_V];//記錄那些已經進入最小生成樹的節點之間的權值 bool used[MAX_V];//用于判斷是否已經進入最小生成樹,false表示否,true表示是 printf("請輸入節點個數與邊數\n"); cin>>V>>E;int Trace[V];fill(mincost,mincost+V+1,INF);//最小生成樹一共有V個節點,V+1條邊 fill(used,used+V,false);//一共有V個節點 //初始化cost[] for(i=0;i<V;i++){for(j=0;j<V;j++){if(i==j) cost[i][j]=0;//節點自己到自己權值為0 else cost[i][j]=INF; }}//向cost[]里面填充各個節點之間的權值 for(m=0;m<E;m++){printf("請輸入兩個端點以及它們之間邊的權值\n");cin>>i>>j>>cost[i][j];cost[j][i]=cost[i][j];//無向圖,中心對稱 }mincost[0]=0; int res=0;//存儲最終的最小生成樹權值和 int count=0;/*遍歷圖,不斷地將沒有加入used中的距離加入used數組的節點權值最小的節點加入used數組。
更新V輪mincost數組,得到最小生成樹。 */while(true)//也可以寫成for(int i=0;i<V;i++) {int v=V;for(m=0;m<V;m++){ if((!used[m])&&(mincost[m]<mincost[v]))v=m; }Trace[count]=v;count++; if(v==V) break;Trace[count]=v;//最后一個跳出來了,沒記錄,要把最后一個節點加入 used[v]=true;res+=mincost[v];for(m=0;m<V;m++){/*取(新加入最小生成樹的節點到其他節點的權值)和記錄在mincost中的到其他節點的權值進行比較,取它們之間的最小值,來更新mincost數組*/ mincost[m]=min(mincost[m],cost[v][m]); }}printf("最小生成樹權值是:\n");cout<<res<<endl;printf("依次找到的節點是:\n");for(int i=0;i<V;i++){cout<<"->"<<Trace[i];}cout<<endl;
}運行結果:
輸入上面單源點最短路徑所示的圖,運行結果如下
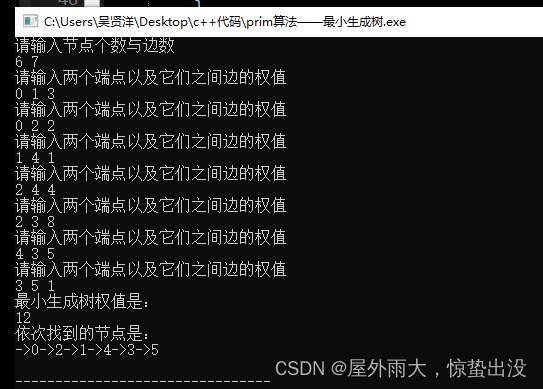
關鍵步驟證明:
視頻證明
時間復雜度與空間復雜度:
時間復雜度與空間復雜度都是0()








)








)
![[matlab]yalmip國內源yalmip下載地址所有版本匯總](http://pic.xiahunao.cn/[matlab]yalmip國內源yalmip下載地址所有版本匯總)
)
:在項目中使用)
