第一題

1.?兩數之和

?????????由上述題意所知，本題要采用二分法的解題思路，二分法主要是面向有序的數組且也滿足二段性的數組，所謂二段性就是在一定的規則下能把該數組分成兩個部分；

? ? ? ? 本題注意要點：

1、循環結束的條件：

? ? ? ? 左指針>右指針時，該循環結束；

2、關于中點的求解公式

? ? ? ? 一般采用左指針+整個數組一半的方法，而不是左右指針之差+1的和除以2，主要是防治后者會發生溢出；

? ? ? ? 綜上所述，代碼如下：

class Solution {public int search(int[] nums, int target) {int left = 0,right = nums.length-1;while(left <= right){//找到中間點，防止溢出int mid = left + (right-left)/2;if(nums[mid] < target){left = mid+1;}else if(nums[mid] > target){right = mid-1;}else{return mid;}}return -1;}
}

故此二分法的樸素解題模版如下所示：

?

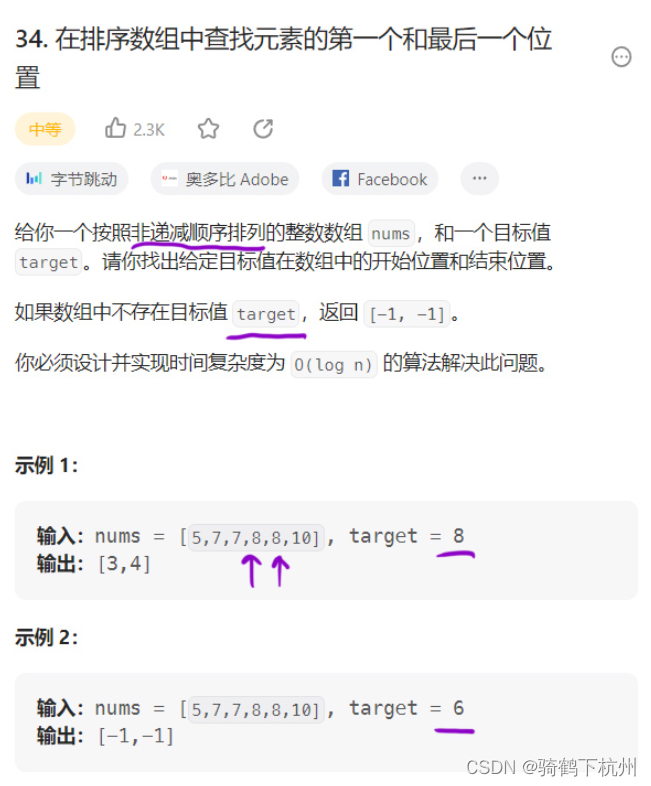
第二題

????????

? ? ? ? ?如上題所示，本題需要通過二分查找的方法來找到一個滿足題意的連續數組，所以簡單來說就需要查找原數組的左右端點；

? ? ? ? 上題中的原數組由于是非遞減，鎖說明滿足二段性，即可以使用二分法；

步驟一：就是來分析如何查找左端點：

細節一：

? ? ? ? 關于循環條件的分析，兩種循環條件如下所示：

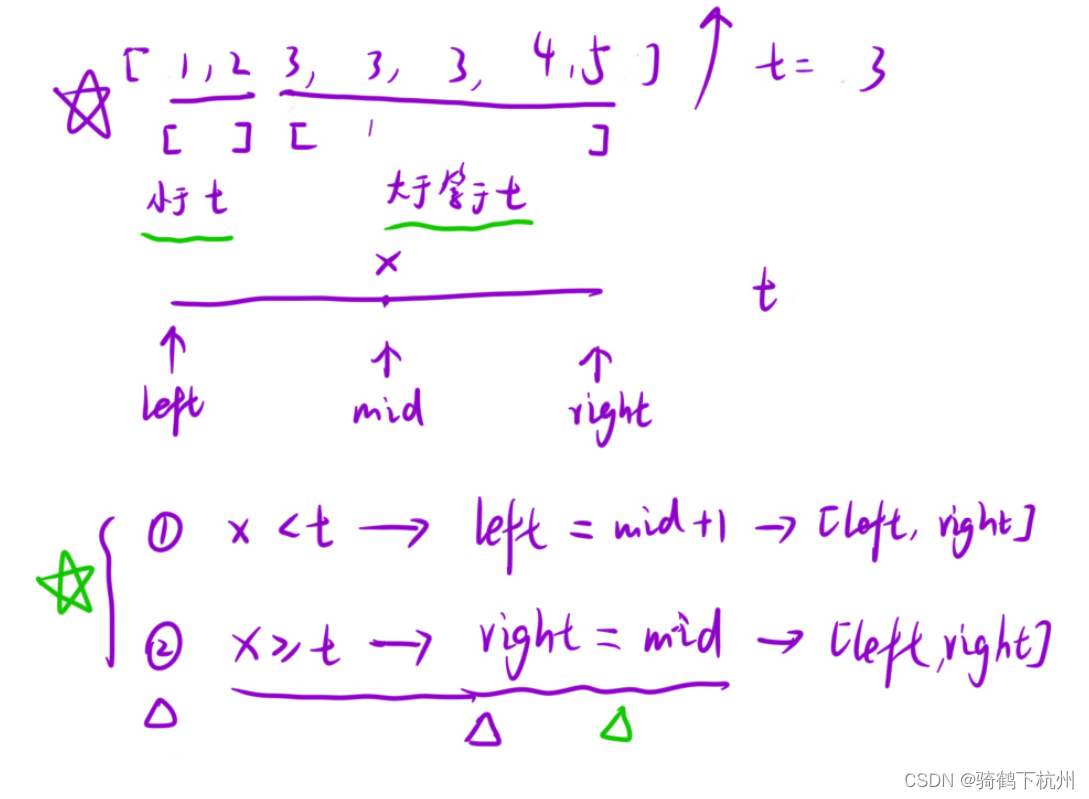
? ? ? ? 如上圖分析，（1,2）左區域里面的數值永遠小于t，（3,3,3,4,5）右區域里面的數可能大于等于t；

? ? ? ? 所以當mid指針所指的數值x接下來右如下分析：

? ? ? ? x<t時，t值的位置在mid右邊，所以更新左指針，left=mid+1，即得到一個新的循環區間；

? ? ? ? x>=t時，t值的位置在mid的左邊或者mid的位置，所以right=mid；

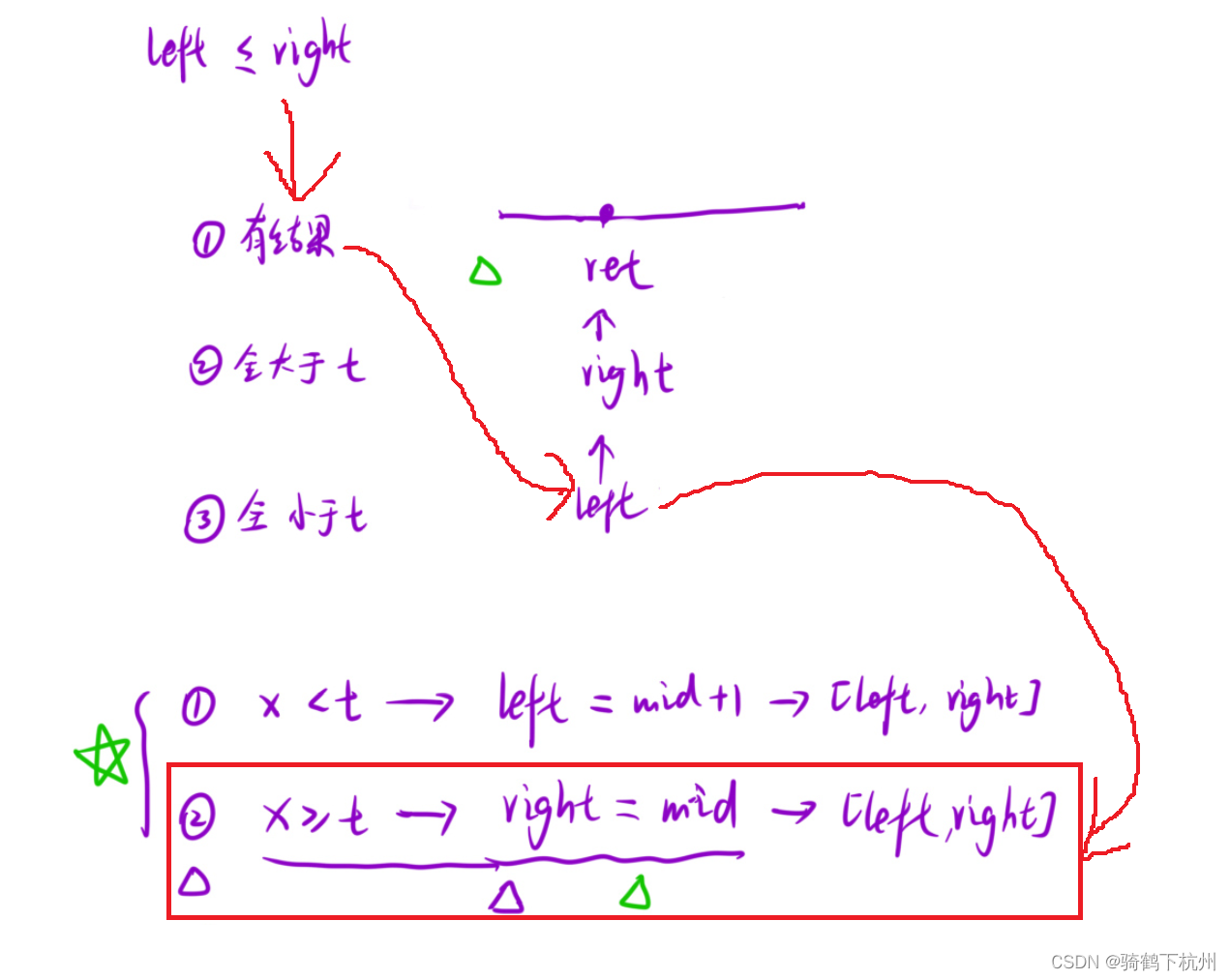
? ? ? ? 所以當我們的判斷條件是left<=right時，做如下分析：

? ? ? ? 如果原數組里有我們需要的結果，左后左指針會與右指針重逢，且指向我們所求的端點，但是由于我們的判斷條件，所以就會一直更新區間；分析圖如下所示：

? ? ? ? 綜上所述：

1、left=right的時候，就已經出現結果了，不需要在進行判斷了；

2、如果在判斷就會出現死循環；

細節二：

? ? ? ? 關于在循環條件時，我們進行中點計算的公式選擇分析：

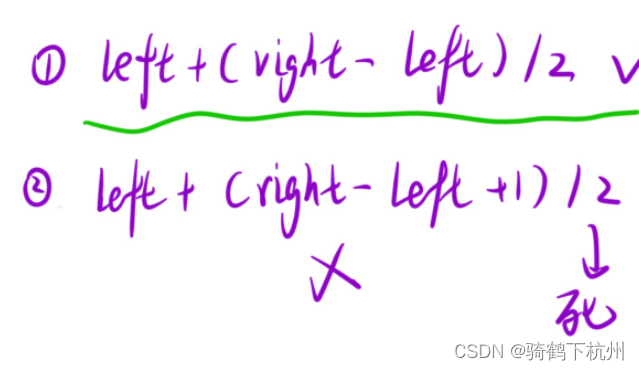
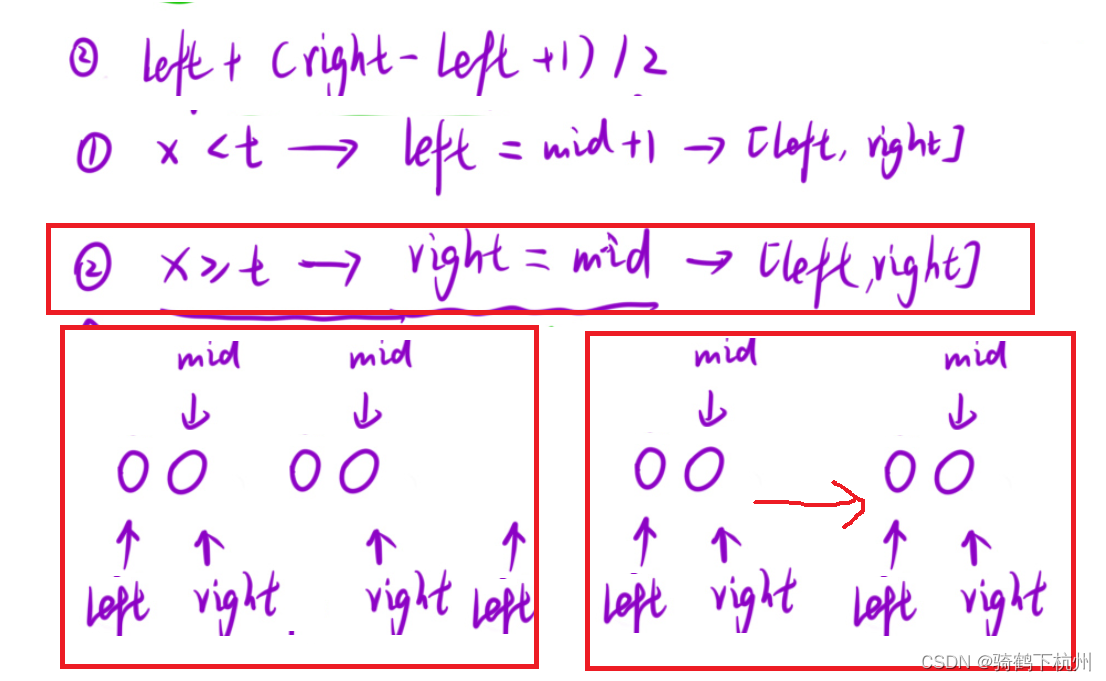
? ? ? ? 有下圖所示，重點選擇的公式有下面兩種方式：

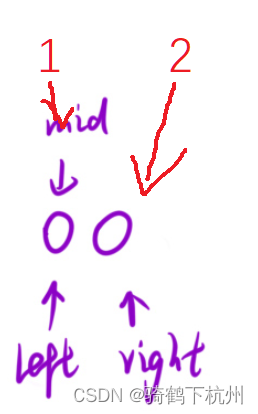
? ? ? ? 上面兩種方法的區別就是當有長度為2的數組是，找到的中點事不同的；

? ? ? ? 第一種方法找到的中點是left，第二種方法找到的中點是right；

? ? ? ? 接下來講第一種中點方法：

????????

? ? ? ? 如上圖所示，第一種中點選擇時，

? ? ? ? x<t時，左指針右移和右指針相等，則得到要判斷的值；

???????? x>=t時，左指針右移兩位，左指針在右指針的右邊，則當前沒有找到需要的點，循環結束；

????????接下來講第二種中點方法：

? ? ? ? 如上圖所示，第二種中點選擇時，

? ? ? ? x<t時，左指針右移兩位，左指針在右指針的右邊，則當前沒有找到需要的點，循環結束；

???????? x>=t時，右指針不變，則進入死循環；

步驟二：就是來分析如何查找右端端點：

細節一：

? ? ? ? 關于循環條件的分析，有上述左端點的分析，我們選擇left<right；

細節二：

? ? ? ? 如上分析，我們選擇

? ? ? ? 分析如下：

分析如上，代碼如下：

????????

class Solution {public int[] searchRange(int[] nums, int target) {int[] ret = new int[2];ret[0]= ret[1] = -1;if(nums.length == 0){return ret;}//1二分左端點int left = 0,right = nums.length-1;while(left < right){int mid = left +(right-left)/2;if(nums[mid] < target){left = mid+1;}else{right = mid;}}//此時做左右指針相遇，接下倆判斷該相遇點的值是否為目標值if(nums[left] != target){return ret;}else{ret[0] = left;}//2、二分右端點left = 0;right = nums.length-1;while(left < right){int mid = left +(right-left+1)/2;if(nums[mid] <= target){left = mid;}else{right = mid-1;}}//此時做左右指針相遇，接下倆判斷該相遇點的值是否為目標值if(nums[left] != target){return ret;}else{ret[1] = right;}return ret;}
}

ps：本次的內容就到這里了，如果大家感興趣的話就請一鍵三連哦！！！?