💓博主CSDN主頁:杭電碼農-NEO💓
?
?專欄分類:高階數據結構專欄?
?
🚚代碼倉庫:NEO的學習日記🚚
?
🌹關注我🫵帶你學習更多數據結構
? 🔝🔝

---

1. 前言

關于圖論,無非就是最小生成樹問題和最短路徑問題. 對于最短路徑問題來說, 分為單源最短路徑和多源最短路徑, 并且圖中的權值是否有負數, 對應能使用的算法也不同

本章重點:

本篇文章著重講解圖的單源最短路徑之Dijkstra算法和bellman-Ford算法.以及多源最短路徑之Floyd-wars hall算法. 文章會著重講解這些算法的思路, 代碼實現部分要靠大家的理解能力了

---

2. 單源最短路徑問題

所謂的單源最短路徑,也就是從圖中任意一點出發, 到圖中每個節點的最短路徑,也就是最小的權值和

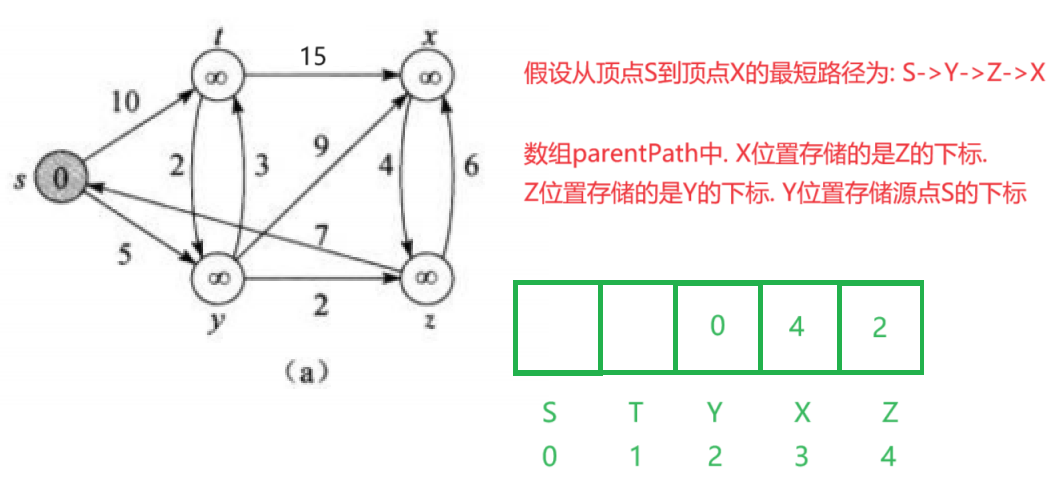
對于單源最短路徑的求解. 我們一般使用輸出型參數. 用兩個數組來表示最短路徑的權值以及最短路徑的路徑.

//存儲任意點到圖中其他點的最短路徑的權值vector<W>& dist//記錄srci->其他頂點最短路徑父頂點數組vector<int>& parentPath

第一個數組很好理解. 圖中的頂點會簡化成為數組中的元素. 所以dist數組中的dist[i]=j.代表頂點i到srci的最短路徑的權值. 不好理解的是第二個數組. 它存儲的是最短路徑的父頂點. 什么意思呢? 請看下圖:

---

3. dijkstra算法講解

針對一個帶權有向圖G，將所有結點分為兩組S和Q，S是已經確定最短路徑的結點集合，在初始時為空（初始時就可以將源節點s放入，畢竟源節點到自己的代價是0），Q 為其余未確定最短路徑的結點集合，每次從Q 中找出一個起點到該結點代價最小的結點u ，將u 從Q 中移出，并放入S 中，對u 的每一個相鄰結點v 進行松弛操作。

松弛即對每一個相鄰結點v ，判斷源節點s到結點u 的代價與u 到v 的代價之和是否比原來s 到v 的代價更小，若代價比原來小則要將s 到v 的代價更新為s 到u 與u 到v 的代價之和，否則維持原樣。如此一直循環直至集合Q 為空，即所有節點都已經查找過一遍并確定了最短路徑，至于一些起點到達不了的結點在算法循環后其代價仍為初始設定的值，不發生變化

定義很抽象,現在來看看實圖:

從S開始,s->y是最短路徑了, 就以y為起點(y的值被更新為5)更新與y相連的t,z,x. 同時s->t也被更新為10. y->t小于s->t. 所以將t重新更新為8. x,z也是同理. 第二次更新完. s->z最短.就以z為起點更新與z相連的x.以此類推.直到所有頂點都在集合S中.

話不多說,上代碼:

void Dijkstra(const V& src, vector<W>& dist, vector<int>& pPath)//Dijkstra算法求解最短路徑,兩個數組,一個存儲兩個點之間的最小權值(從src點,到圖中其他的點),另一個存父路徑節點下標
{size_t srci = GetIndex(src);size_t n = _vertex.size();dist.resize(n, MAX_W);pPath.resize(n, -1);dist[srci] = W();pPath[srci] = srci;vector<bool> check(n, false);//此數組中存放已經確定了的最短路勁的節點for(int j=0;j<n;j++)//n個節點,一共會更新n次,也可以判斷check數組中的元素是否全為true{//選最短路徑的頂點更新其他路徑(不在s中)int u = 0;//最小的點的下標W minu = MAX_W;//最小的點的權值for (int i = 0; i < n; i++)//選擇dist數組中權值最小的,作為起始點來進行松弛操作{if (check[i] == false && dist[i] < minu){u = i;minu = dist[i];check[i] = true;}}//進行松弛更新,srci->u, u->其他頂點(v), srci->v就可以更新出來for (int v = 0; v < n; v++)//從0到n,把與u點相連的所有頂點都找出來更新{if (_edge[u][v] != MAX_W && dist[u] + _edge[u][v] < dist[v])//若srci->u+u->v的距離小于dist[v]的大小,則更新他{dist[v] = dist[u] + _edge[u][v];pPath[v] = u;}}}
}

此算法只適用于不帶負權路徑的圖
若有不懂,歡迎私信

---

4. bellman-Ford算法講解

Dijkstra算法只適用于不帶負權路徑的圖, 具體的原因可以參考這篇文章: 負權路徑帶來的后果

顯而易見, bellman算法可以解決帶負權路徑的圖

說白了此算法就是一個暴力求解的過程, 它的時間復雜度是O(N^3). 它的思路就是以所有頂點為起始點,更新所有相連的邊

更新次序就是(t，z)，(t，y)，(t，z)，(y,x)，(y，z), (z,x), (z，s), (s,t), (s,y). 更新(y,z)時,由于更新后的值是7+9=16>2,所以不會更新這條邊. 其他更新邊也是同理. 但是這樣暴力更新一次并不能解決問題,因為假如只更新一次, (s,t)的值就是6, 但是顯而易見, s->y->x->t的權值是2,要小于6. 出現這種情況的原因是, 還沒有以x為起始點進行更新其他點時, 根本就不知道x->t這條路. 所以我們需要以所有點為起始點更新n次,n是頂點的數量

上代碼:

bool BellmanFord(const V& src, vector<W>& dist, vector<int>& pPath)//貝爾曼-福特算法求解最短路徑
{size_t srci = GetIndex(src);size_t n = _vertex.size();dist.resize(n, MAX_W);pPath.resize(n, -1);dist[srci] = W();//用i->j,圖中的所有邊去更新for (int k = 0; k < n; k++)//再套一層循環的原因是,只更新一輪可能會有問題,更新K輪一定不會有問題{bool check = false;for (int i = 0; i < n; i++){for (int j = 0; j < n; j++){if (_edge[i][j] != MAX_W && dist[i] + _edge[i][j] < dist[j])//若這條邊存在,并且從i->j要少于直接0->j{dist[j] = dist[i] + _edge[i][j];pPath[j] = i;check = true;}}}if (check == true) breal;}//有可能K輪循環后,會形成閉環return true;
}

很明顯它的時間復雜度是O(N^3)

---

5. 多源最短路徑問題

說白了就是任意兩點之間的最短路徑
Floyd-Warshall算法就是解決方法之一

和單源最短路徑算法的思路相似. 這里需要用到兩個數組, 只不過這里是用兩個二維數組, 一個二維數組存儲頂點i->j的最短路徑值, 另外一個數組存儲 (i,j)的父節點下標. i,j是最短路徑的中間某節點

---

6. Floyd-Warshall算法講解

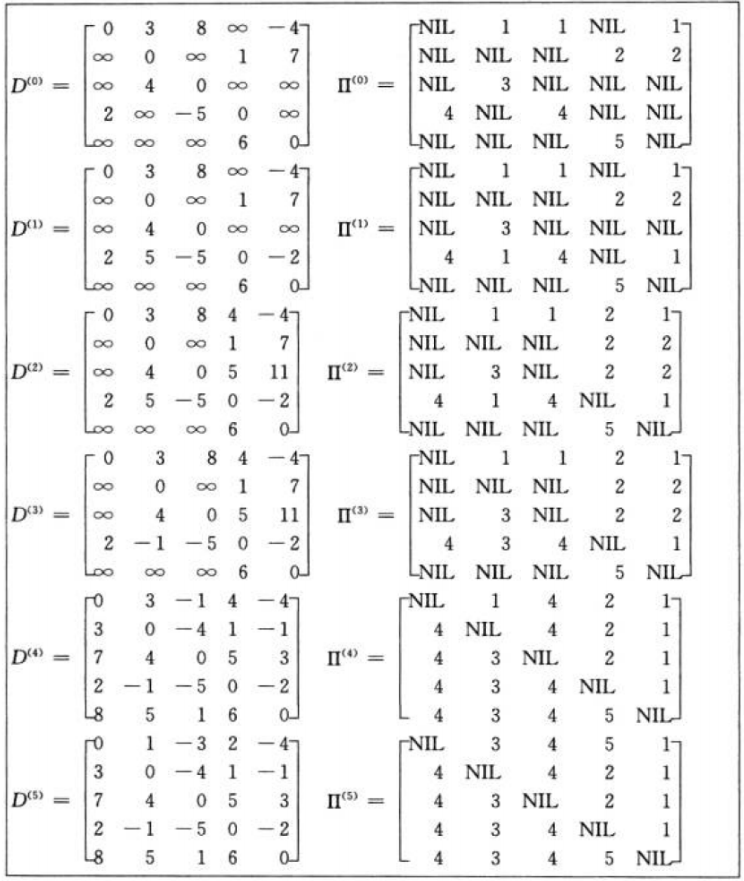
Floyd算法考慮的是一條最短路徑的中間節點，即簡單路徑p={v1,v2,…,vn}上除v1和vn的任意節
點。設k是p的一個中間節點，那么從i到j的最短路徑p就被分成i到k和k到j的兩段最短路徑p1，p2。p1是從i到k且中間節點屬于{1，2，…，k-1}取得的一條最短路徑。p2是從k到j且中間節點屬于{1，2，…，k-1}取得的一條最短路徑

你可能覺得很抽象,下面來個實際案例:

上代碼:

void FloydWarShall(vector<vector<W>>& vvDist, vector<vector<int>>& vvpPath)//多源最短路徑求解問題(任意兩點的最短路徑),數組vvDist中包含了所有點的最短距離
{size_t N = _vertex.size();vvDist.resize(N);vvpPath.resize(N);for (int i = 0; i < N; i++){vvDist[i].resize(N, MAX_W);vvpPath[i].resize(N, -1);}//把直接相連的邊給更新一下,后續就不需要_edge數組了for (int i = 0; i < N; i++){for (int j = 0; j < N; j++){if (_edge[i][j] != MAX_W)//直接相連{vvDist[i][j] = _edge[i][j];vvpPath[i][j] = i;//起點是i,目前的父路徑暫時是i(后面可能會是K)}if (i == j)vvDist[i][j] = W();}}//最短路徑的更新,i->j,中間可能經過了k個頂點,i->{其他頂點(最多是N-2)}->j//k作為i,j的中間點,k可以是任意頂點,k可以是1,2,3,任意點,要把所有點拿來更新for (int k = 0; k < N; k++)//雖然是最多只需要走n-2個點,但是這里除掉的兩個點我們并不知道是哪兩個,所以都需要走一遍{for (int i = 0; i < N; i++){for (int j = 0; j < N; j++){//以K作為中間的去更新i->j的路徑if (vvDist[i][k] != MAX_W && vvDist[k][j] != MAX_W && vvDist[i][k] + vvDist[k][j] < vvDist[i][j])//i->k的路徑和k->j的路徑都存在,并且i->k加上k->j的路徑小于i直接到j{vvDist[i][j] = vvDist[i][k] + vvDist[k][j];vvpPath[i][j] = vvpPath[k][j];//這里j的父路徑不能直接寫成k,因為k->j中間可能還有其他點,比如k->x->y->j,最開始的i,j是在_edge數組中取得,而這里應該是從vvppath[k][j]中取得,需要找跟j相連的上一個頂點}}}}
}

---

7. 總結

圖論總體來說比較抽象,很難理解這些算法的思路. 但是也不用慌張,圖論本身就屬于加分項, 你知道算法原理即可, 不用會手撕, 換個角度, 面試官也不一定能手撕這些算法.

---

🔎 下期預告:LRU cache講解 🔍