HNU-算法設計與分析-作業5

第五次作業【回溯算法】

在這里插入圖片描述

文章目錄

    • 第五次作業【回溯算法】
      • <1> 算法分析題5-3 回溯法重寫0-1背包
      • <2> 算法分析題5-5 旅行商問題（剪枝）
      • <3> 算法實現題5-2 最小長度電路板排列問題
      • <4> 算法實現題5-7 n色方柱問題
      • <5> 算法實現題5-13 任務分配問題

<1> 算法分析題5-3 回溯法重寫0-1背包

▲問題重述

一共有N件物品，第i（i從0開始）件物品的重量為weight[i]，價值為value[i]。在總重量不超過背包承載上限maxw的情況下，求能夠裝入背包的最大價值是多少？并要求輸出選取的物品編號。

（要求使用回溯法求解）

▲解題思路

使用回溯法。構造解空間樹，從第0層到第n-1層，每層表示對于背包內某個物品的“取”或“不取”。第n層為答案層，在第n層進行判定結果是否是想要的（即能不能獲得更優的解），若是就做出相應的處理。

這是一個萬能的解空間樹圖，借來用用。

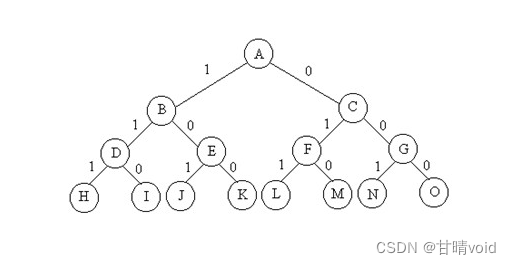
在這里插入圖片描述

剪枝想法：

（1）如果在第n層之前，就出現了總和大于的maxw情況，那么此時已經超重了。之后無論是否取，都不可能再得到總和小于maxw的結果了。這種情況以及它的子樹直接刪去即可。

（2）如果在第n層之前，目前已有的價值，即使加上剩余可取的最大價值，也不能達到已經達到的bestv，那么之后即使全部取也不能達到bestv了。這種情況及它的子樹直接刪去即可。

剪枝代碼可以刪去，不影響結果，但會降低效率。

▲代碼

// -*- coding:utf-8 -*-// File    :   01背包問題（回溯）.cpp
// Time    :   2023/12/14
// Author  :   wolf#include <iostream>
using namespace std;int w[5000];
int v[5000];
bool flag[5000];
bool ans[5000];
int now_w = 0, now_v = 0;
int n, maxw, bestv = 0;
int rest_v;void backtrace(int depth)
{if (depth == n) // 到達第n層：答案{if (now_v > bestv && now_w <= maxw) // 答案是需要打印的{bestv = now_v;for (int i = 0; i < n; i++){ans[i] = flag[i];}}return;}if (depth < n && now_w > maxw)return; // 剪枝：此時背包已經過重if (now_v + rest_v <= bestv)return; // 剪枝：此時剩余價值即使全部拾取也無法達到最大價值rest_v -= v[depth];// 取這個物品now_v += v[depth];now_w += w[depth];flag[depth] = 1;backtrace(depth + 1);now_v -= v[depth];now_w -= w[depth];flag[depth] = 0;// 不取這個物品backtrace(depth + 1);rest_v += v[depth];return;
}int main()
{cin >> maxw >> n;for (int i = 0; i < n; i++){cin >> w[i] >> v[i];ans[i] = 0;flag[i] = 0;rest_v += v[i];}backtrace(0);for (int i = 0; i < n; i++){if (ans[i])cout << i << " ";}cout << endl;cout << bestv << endl;return 0;
}

▲驗證

洛谷P1048（https://www.luogu.com.cn/problem/P1048）

【驗證時把輸出最優解向量的for循環刪去，題目要求不一樣】

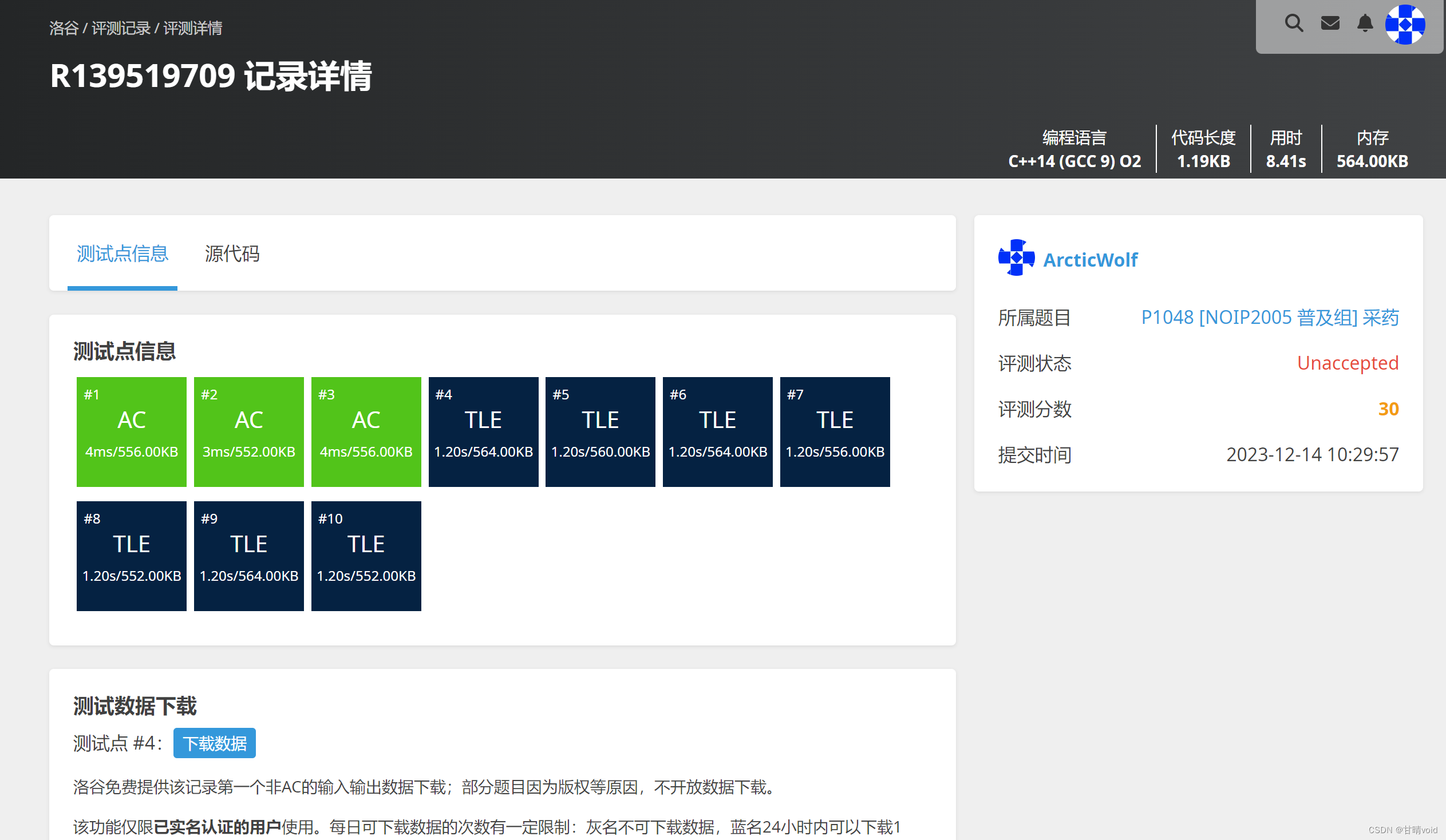
在這里插入圖片描述

回溯法解決背包問題的O(2n)還是從數量級上顯著不如動態規劃的O(n2)。

故在數據量很大的時候，不能通過測評，顯示超時。

所以01背包問題還是得用動態規劃解，本題只是練習一下回溯法。

<2> 算法分析題5-5 旅行商問題（剪枝）

▲題目重述

在這里插入圖片描述

▲解答

在這里插入圖片描述

▲代碼

// -*- coding:utf-8 -*-// File    :   5-5 旅行售貨員問題.cpp
// Time    :   2023/12/30
// Author  :   wolf#include <iostream>using namespace std;
int const MAXINT = 99999;
int map[1000][1000];
int v, e, best_cost = MAXINT, now_cost = 0;
int now_order[1000]; // 儲存當前排列解向量
int ans[1000];       // 儲存結果排列解向量
int upbound;void swap(int a, int b)
{int temp = now_order[a];now_order[a] = now_order[b];now_order[b] = temp;
};void backtrack(int depth)
{if (depth == v - 1) // 到達答案層{if (map[now_order[depth]][now_order[0]] != -1) // 能跟第一個相連{now_cost += map[now_order[depth]][now_order[0]];if (now_cost < best_cost) // 更優，保存結果{best_cost = now_cost;for (int i = 0; i < v; i++){ans[i] = now_order[i];}}now_cost -= map[now_order[depth]][now_order[0]];}}else{for (int i = depth; i < v; i++) // 生成排列樹當前向量中depth位置的節點編號（第depth個訪問哪個節點）{if (map[now_order[depth - 1]][now_order[i]] != -1) // 前一節點到當前的這個節點有可達邊{if (now_cost + map[now_order[depth - 1]][now_order[i]] <= upbound)// 剪枝：若當前步驟使得費用和就大于上界了，不必繼續{swap(i, depth);now_cost += map[now_order[depth - 1]][now_order[depth]];backtrack(depth + 1);now_cost -= map[now_order[depth - 1]][now_order[depth]];swap(i, depth);}}}}return;
}
int main()
{cin >> v >> e;for (int i = 0; i < v; i++)for (int j = 0; j < v; j++)map[i][j] = -1;for (int i = 0; i < e; i++){int a, b, weight;cin >> a >> b >> weight;map[a][b] = weight;map[b][a] = weight;}// 剪枝預備：for (int i = 0; i < v; i++){int i_out_max = 0; // 存儲從i節點向外for (int j = 0; j < v; j++){i_out_max = max(i_out_max, map[i][j]);}upbound += i_out_max;}// 指定從0號節點開始遍歷// 反正最后每一個節點都需要遍歷過for (int i = 0; i < v; i++)now_order[i] = i; // 初始按照遞增順序（初始順序是無所謂的，只要保證都能遍歷一遍就可以）backtrack(1);         // 0號節點已固定，搜索從1號節點開始的全排列cout << best_cost << endl;return 0;
}

▲驗證

input
4 5
0 1 10
0 2 15
1 2 35
1 3 25
2 3 30output
50

<3> 算法實現題5-2 最小長度電路板排列問題

▲問題重述

在這里插入圖片描述

▲解題思路

排列樹解決問題。創建以下函數/類

  1. Board 類:
    • class Board 定義了一個名為 Board 的類，用于處理電路板排列問題。
    • 私有成員變量包括 n（電路板數）、m（連接塊數）、x（當前解的數組）、bestx（當前最優解的數組）、bestd（當前最優密度）、low（輔助數組，存儲連接塊的最小高度）、high（輔助數組，存儲連接塊的最大高度）、B（連接塊數組）。
  2. len 函數:
    • int len(int ii) 用于計算排列中的某一部分的長度，即連接塊之間的最大高度差。
    • 該函數首先將 low 和 high 數組初始化為合適的值，然后根據當前排列計算連接塊的最小和最大高度，最后計算最大高度差并返回。
  3. Backtrack 函數:
    • void Backtrack(int i) 是一個遞歸函數，用于在排列樹上進行回溯搜索，尋找最優解。
    • 當達到排列樹的終點（i == n）時，計算當前排列的長度，并更新最優解。
    • 否則，對于當前位置 i，嘗試選擇不同的電路板進行交換，然后繼續遞歸搜索。
  4. ArrangeBoards 函數:
    • int ArrangeBoards(int **B, int n, int m, int *bestx) 是主要的調用函數。
    • 在該函數中，創建一個 Board 類的實例 X，并通過初始化設置其成員變量。
    • 利用回溯算法調用 Backtrack(1) 來找到最優解。
    • 返回最優解的密度。
  5. main 函數:
    • main 函數讀取輸入，調用 ArrangeBoards 函數來解決問題，并輸出結果。
    • 動態分配二維數組 B 以存儲連接塊信息。
    • 讀取輸入的電路板連接信息。
    • 創建數組 bestx 用于存儲最優解。
    • 輸出最優解的密度和排列。

▲代碼

// 電路板排列問題
#include <bits/stdc++.h>
using namespace std;
class Board
{friend int ArrangeBoards(int **, int, int, int *);private:void Backtrack(int i);int len(int ii);int n,      // 電路板數m,      // 連接塊數*x,     // 當前解*bestx, // 當前最優解bestd,  // 當前最優密度*low,   //*high,  //**B;    // 連接塊數組
};
int Board::len(int ii)
{for (int i = 0; i <= m; i++){high[i] = 0;low[i] = n + 1;}for (int i = 1; i <= ii; i++){for (int k = 1; k <= m; k++){if (B[x[i]][k]){if (i < low[k])low[k] = i;if (i > high[k])high[k] = i;}}}int tmp = 0;for (int k = 1; k <= m; k++){if (low[k] <= n && high[k] > 0 && tmp < high[k] - low[k])tmp = high[k] - low[k];}return tmp;
}
void Board::Backtrack(int i) // 回溯搜索排列樹
{if (i == n) // 到達排列樹終點{int tmp = len(i);if (tmp < bestd){bestd = tmp;for (int j = 1; j <= n; j++)bestx[j] = x[j];}}else{for (int j = i; j <= n; j++) // 選擇x[j]為下一塊電路板{swap(x[i], x[j]);int ld = len(i);if (ld < bestd)Backtrack(i + 1);swap(x[i], x[j]);}}
}
int ArrangeBoards(int **B, int n, int m, int *bestx)
{Board X;// 初始化XX.x = new int[n + 1];X.low = new int[m + 1];X.high = new int[m + 1];X.B = B;X.n = n;X.m = m;X.bestx = bestx;X.bestd = n + 1;// 初始化total和nowfor (int i = 1; i <= n; i++){X.x[i] = i;}X.Backtrack(1);delete[] X.x;delete[] X.low;delete[] X.high;return X.bestd;
}
int main()
{int n, m;cin >> n >> m;int **B = new int *[n + 1];for (int i = 0; i <= n; i++)B[i] = new int[m + 1];for (int i = 1; i <= n; i++)for (int j = 1; j <= m; j++)cin >> B[i][j];int *bestx = new int[n + 1];for (int i = 1; i <= n; i++)bestx[i] = 0;int ans = ArrangeBoards(B, n, m, bestx);cout << ans << endl;for (int i = 1; i <= n; i++)cout << bestx[i] << " ";cout << endl;return 0;
}

▲驗證

測試案例

8 5
1 1 1 1 1
0 1 0 1 0
0 1 1 1 0
1 0 1 1 0
1 0 1 0 0
1 1 0 1 0
0 0 0 0 1
0 1 0 0 1

測試結果：

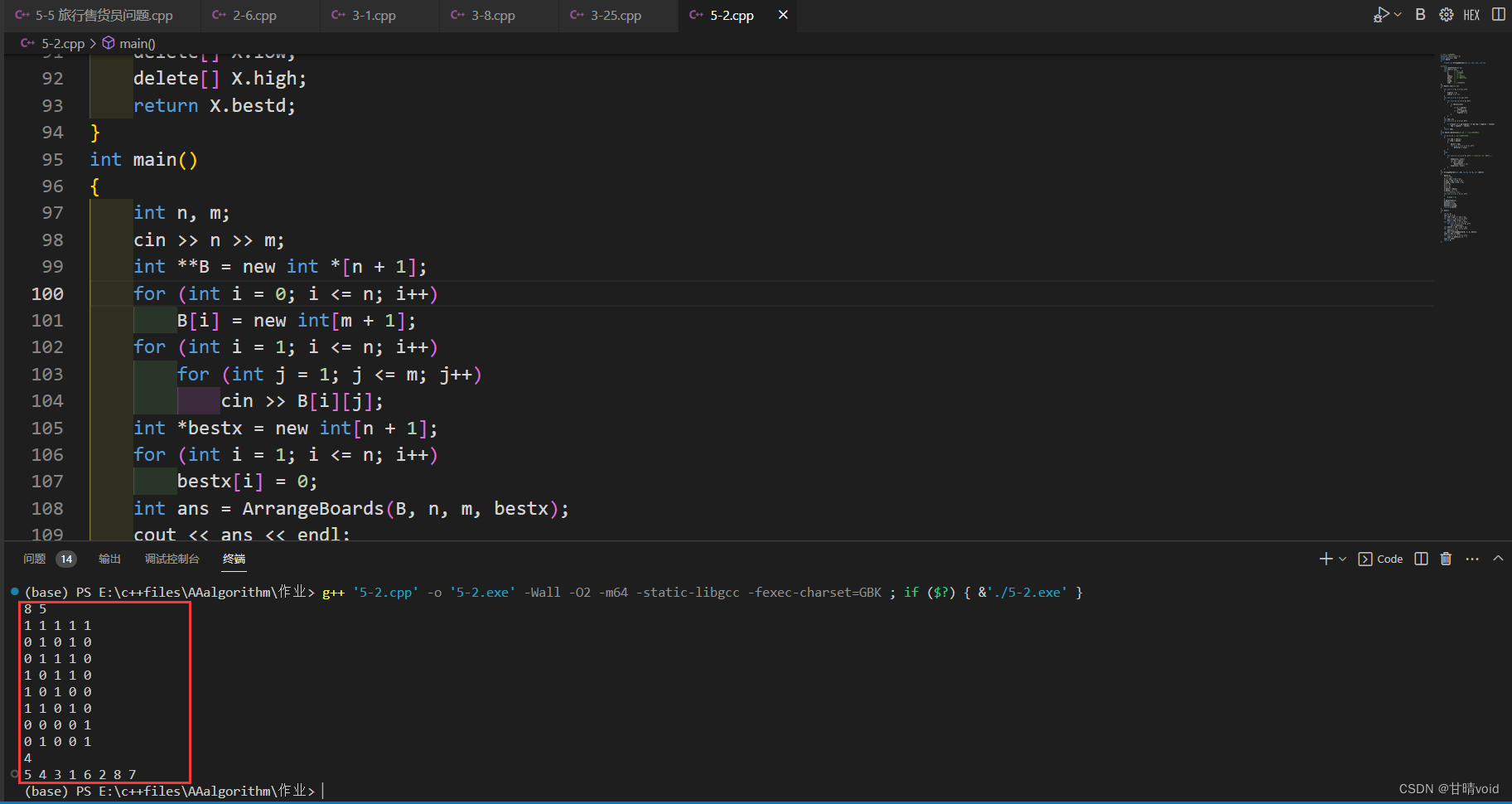
在這里插入圖片描述

<4> 算法實現題5-7 n色方柱問題

▲問題重述

設有 n 個立方體，每個立方體的每一面用紅、黃、藍、綠等 n 種顏色之一染色。要把這n 個立方體疊成一個方形柱體，使得柱體的 4 個側面的每一側均有 n 種不同的顏色。試設計一個回溯算法，計算出 n 個立方體的一種滿足要求的疊置方案。

對于給定的 n 個立方體以及每個立方體各面的顏色，計算出 n 個立方體的一種疊置方案，使得柱體的 4 個側面的每一側均有 n 種不同的顏色。

數據輸入：

第一行有 1 個正整數 n，0< n< 27，表示給定的立方體個 數和顏色數均為 n。第 2 行是 n 個大寫英文字母組成的字符串。該字符串的第 k(0≤ k< n) 個字符代表第 k 種顏色。接下來的 n 行中，每行有 6 個數，表示立方體各面的顏色。立方體各面的編號如下圖所示。

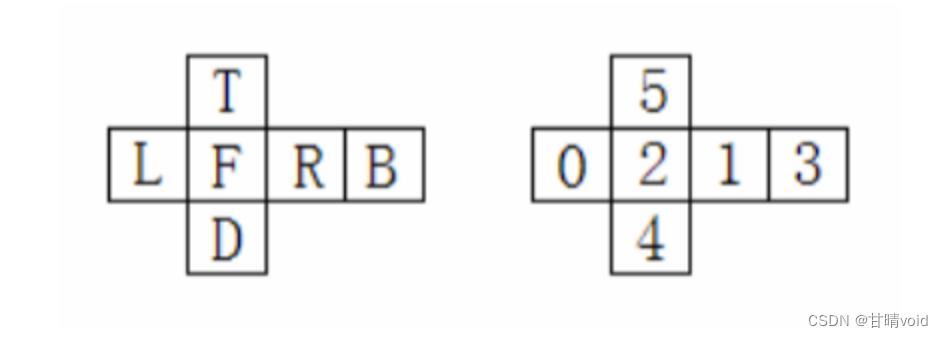
在這里插入圖片描述

圖中 F 表示前面，B 表示背面，L 表示左面，R 表示右面，T 表示頂面，D 表示底面。相 應地，2 表示前面，3 表示背面，0 表示左面，1 表示右面，5 表示頂面，4 表示底面。
例如，在示例輸出文件中，第3行的6個數0 2 1 3 0 0分別表示第1個立方體的左面的顏色為R, 右面的顏色為B, 前面的顏色為G, 背面的顏色為Y, 底面的顏色為R, 頂面的顏色為 R。

案例：

input
4
RGBY
0 2 1 3 0 0 
3 0 2 1 0 1
2 1 0 2 1 3
1 3 3 0 2 2 output
RBGYRR
YRBGRG
BGRBGY
GYYRBB

▲解題思路

在下面的代碼中使用注釋講解。使用回溯法的思路套用回溯法的模板，但有改動。

本題比較晦澀難懂，在理解上需要花很多時間。

關于代碼部分的映射方式

在這里插入圖片描述

▲代碼

// -*- coding:utf-8 -*-// File    :   5-7 n色方柱問題.cpp
// Time    :   2023/12/27
// Author  :   wolf#include <iostream>using namespace std;
char color[28]; // 用來儲存輸入的數字對應的顏色（只在輸出的時候轉換為字符，在做題時使用數字存儲）
int box[28][6]; // box[i][j]用來儲存第i個立方體各個面（即第j面）的顏色
int n;
int count = 1; //  標記這是第幾個輸出的；可能結果
const int place[24][6] = {// 轉動立方體的映射函數，使用box[depth+1][j]=origin[place[method][j]]來獲取第method種方法下下一層的擺放方式// place[i][j]為第i種轉換方法下該立方體該層的第j面應該變換為place[i][j]{0, 1, 2, 3, 4, 5},{4, 5, 2, 3, 1, 0},{1, 0, 2, 3, 5, 4},{5, 4, 2, 3, 0, 1}, // 2為底面，3為頂面{0, 1, 3, 2, 4, 5},{4, 5, 3, 2, 1, 0},{1, 0, 3, 2, 5, 4},{5, 4, 3, 2, 0, 1}, // 3為底面，2為頂面{3, 2, 0, 1, 4, 5},{4, 5, 0, 1, 2, 3},{2, 3, 0, 1, 5, 4},{5, 4, 0, 1, 3, 2}, //  0為底面，1為頂面{3, 2, 1, 0, 4, 5},{4, 5, 1, 0, 2, 3},{2, 3, 1, 0, 5, 4},{5, 4, 1, 0, 3, 2}, //  1為底面，0為頂面{1, 0, 4, 5, 3, 2},{3, 2, 4, 5, 0, 1},{0, 1, 4, 5, 2, 3},{2, 3, 4, 5, 1, 0}, //  4為底面，5為頂面{1, 0, 5, 4, 3, 2},{3, 2, 5, 4, 0, 1},{0, 1, 5, 4, 2, 3},{2, 3, 5, 4, 1, 0}, //  5為底面，4為頂面
};void backtrack(int depth)
{// cout << "depth=" << depth << endl;if (depth == n - 1) // 到達答案層{cout << "Possible Solution " << count << " : " << endl;count++;for (int i = 0; i < n; i++){for (int j = 0; j < 6; j++){cout << color[box[i][j]] << " ";}cout << endl;}cout << endl;}else{int process = depth + 1;int origin[6];// 【使用origin[]數組先保存原始情況，可以省去整體恢復原狀的步驟，24次for循環每次都是新的開始】for (int i = 0; i < 6; i++)      // 保存待處理層初始存放的顏色origin[i] = box[process][i]; // origin[i]表示該層初始第i個面存放的顏色// cout << "origin=" << endl;// for (int i = 0; i < 6; i++)//     cout << origin[i] << " ";// cout << endl;for (int i = 0; i < 24; i++) // 列舉子集樹，每個立方體有24種放法,第i種方法{// cout << "method = " << i << endl;for (int j = 0; j < 6; j++) // 按照該種方案的映射，把處理的該層立方體先擺好{box[process][j] = origin[place[i][j]];}// 接下來看這種擺法是否可行int flag = 1; // 初始標記，表示可行// 表示遍歷某個側面時，是否出現重復顏色，used_i[j]標記第i個側面第j號顏色是否被用過，初始清零int used_0[n];int used_1[n];int used_2[n];int used_3[n];for (int i = 0; i < n; i++) //{used_0[i] = 0;used_1[i] = 0;used_2[i] = 0;used_3[i] = 0;}for (int i = 0; i <= process; i++) // 遍歷到現在所有已經放好的立方體，查看每個側面是否有重復的顏色{used_0[box[i][0]]++;used_1[box[i][1]]++;used_2[box[i][2]]++;used_3[box[i][3]]++;if (used_0[box[i][0]] > 1 || used_1[box[i][1]] > 1 || used_2[box[i][2]] > 1 || used_3[box[i][3]] > 1)// 題目要求是最后擺好的整個立方體條的每個側面都要有n種顏色// 但因為n個立方體擺出的，該側面條有n種顏色，所以相當于每個立方體在該側面的顏色都不一樣// 即某個側面條上每種顏色只能使用一次，這里轉換了題目的條件// 某個側面條上某個顏色用了不止一次，不符合條件，該方案以及該方案的子樹剪掉{flag = 0;// cout << used_0[box[i][0]] << " " << used_1[box[i][1]] << " " << used_2[box[i][2]] << " " << used_3[box[i][3]] << endl;break;}}if (flag == 1) // 目前所有已經擺好的立方體的每個側面都沒有重復的顏色，符合要求，可以繼續放下一個立方體backtrack(depth + 1);}}return;
}int main()
{cin >> n;for (int i = 0; i < n; i++){cin >> color[i];}for (int i = 0; i < n; i++){for (int j = 0; j < 6; j++){cin >> box[i][j];}}cout << endl<< "ans = " << endl;backtrack(-1);return 0;
}

▲驗證

未找到在線測評，使用題目給出的案例

input
4
RGBY
0 2 1 3 0 0 
3 0 2 1 0 1
2 1 0 2 1 3
1 3 3 0 2 2

輸出結果如下：

ans = 
Possible Solution 1 : 
R B G Y R R 
Y R B G R G 
B G R B G Y 
G Y Y R B BPossible Solution 2 :
B R G Y R R
R Y B G G R
G B R B Y G
Y G Y R B BPossible Solution 3 :
R B Y G R R
Y R G B R G
B G B R G Y
G Y R Y B BPossible Solution 4 :
B R Y G R R
R Y G B G R
G B B R Y G
Y G R Y B BPossible Solution 5 :
Y G R B R R
G B Y R R G
B R B G G Y
R Y G Y B BPossible Solution 6 :
G Y R B R R
B G Y R G R
R B B G Y G
Y R G Y B BPossible Solution 7 :
Y G B R R R
G B R Y R G
B R G B G Y
R Y Y G B B Possible Solution 8 :
G Y B R R R
B G R Y G R
R B G B Y G
Y R Y G B B

可見答案不唯一（顯然可能），題目給定的答案在其中之一。

我們這種算法的時間復雜度O(n*24^n)，數據量大了之后可能會很慢。

<5> 算法實現題5-13 任務分配問題

▲問題重述

問題描述: 設有n件工作分配給n個人。將工作i分配給第j個人所需的費用為 cij。試設計一個算法，為每一個人都分配1 件不同的工作，并使總費用達到最小。

算法設計：設計一個算法，對于給定的工作費用，計算最佳工作分配方案，使總費用達到最小。

數據輸入：第一行有1 個正整數n (1≤n≤20)。接下來的n行，每行n個數，表示工作費用。

樣例：

input
3
10 2 3
2 3 4
3 4 5output
9

▲解題思路

假設人不動，將工作分發給不同人。

解向量x[i]為第i個人被分配第x[i]個工作，解空間樹為排列樹。從第0層開始，第0層就有n個節點（可以認為第-1層有一個節點），答案層在第n層（第n-1層將自己與自己交換，實際上不影響最終結果）。在第n層比較當前總費用是不是比目前保存的方案總費用更少，如果是就將這個更小的存下來，否則不做處理。

遍歷完整個排列樹后得到最優解。

▲代碼

// -*- coding:utf-8 -*-// File    :   5-13.cpp
// Time    :   2023/12/25
// Author  :   wolf#include <iostream>using namespace std;
const int MAXNUM = 9999999;
int c[21][21];
int x[21];
int nowcost = 0, mincost = MAXNUM, n;void swap(int a, int b)
{int temp = x[a];x[a] = x[b];x[b] = temp;
}void backtrack(int depth)
{if (depth == n) // 答案層{mincost = min(mincost, nowcost);// cout << nowcost << endl;// 不需要輸出解向量，故不用保存解向量}else{for (int i = depth; i < n; i++){// depth當前人，i為待分發物品序號，人不動，發物品nowcost += c[x[i]][depth];swap(i, depth);backtrack(depth + 1);swap(i, depth);nowcost -= c[x[i]][depth];}}
}int main()
{cin >> n;for (int i = 0; i < n; i++){for (int j = 0; j < n; j++){cin >> c[i][j];}}for (int i = 0; i < n; i++)x[i] = i;backtrack(0);cout << mincost << endl;return 0;
}

▲驗證

測試數據可通過。

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/diannao/13212.shtml
繁體地址，請注明出處：http://hk.pswp.cn/diannao/13212.shtml
英文地址，請注明出處：http://en.pswp.cn/diannao/13212.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！

相關文章

時間格式數據向前或向后歸于整時

時間格式數據向前或向后歸于整時

假設你有一個“時:分:秒”的時間格式數據&#xff0c;例如"12:34:56"&#xff0c;你想要將它向前歸整于整時或者向后歸整于整時&#xff0c;可以按照以下方法進行處理&#xff1a; 1、向前歸整于整時&#xff1a;將分鐘和秒數設置為0 import datetime# 原始時間 ti…
閱讀更多...
公共字段填充(AOP的使用)

公共字段填充(AOP的使用)

Thread是線程池,ThreadLocal是線程變量,每個線程變量是封閉的,與其它線程變量分隔開來,在sky-common下的com.sky.context包下有一個Basecontext類 public class BaseContext {//每一個上下文創建了一個線程變量,用來存儲long類型的id//創建三個方法,用來設置,取用,刪除idpubli…
閱讀更多...
絕地求生：PGS3參賽隊伍跳點一覽，17壓力有點大，4AM與PeRo大概率不roll點

絕地求生：PGS3參賽隊伍跳點一覽，17壓力有點大，4AM與PeRo大概率不roll點

在PCL春季賽結束后&#xff0c;PGS3的參賽隊伍名單以及分組就正式確定了&#xff0c;最后確定名額的DDT和NH被安排在了A組和B組&#xff0c;感覺這次PGS3的分組比較均衡&#xff0c;沒有“死亡之組”一說。這段時間已經有網友匯總了PGS3隊伍在各個地圖的跳點&#xff0c;并且把…
閱讀更多...
「AIGC算法」近鄰算法原理詳解

「AIGC算法」近鄰算法原理詳解

本文主要介紹近鄰算法原理及實踐demo。 一、原理 K近鄰算法&#xff08;K-Nearest Neighbors&#xff0c;簡稱KNN&#xff09;是一種基于距離的分類算法&#xff0c;其核心思想是距離越近的樣本點&#xff0c;其類別越有可能相似。以下是KNN算法的原理詳解&#xff1a; 1. 算…
閱讀更多...
python安裝ESPHome

python安裝ESPHome

1. powershell輸入python 或者 python3 可以查看python版本&#xff0c;沒安裝則會自動跳出微軟商店&#xff0c;安裝即可(注意這里會自動安裝在C盤默認路徑) 2. pip3 install esphome -i https://mirrors.aliyun.com/pypi/simple 3. 根據報錯信息找到esphome的安裝目錄&…
閱讀更多...
python腳本編輯oss文件

python腳本編輯oss文件

1、安裝oss2庫 rootubuntu:~# pip3 install oss2 Collecting oss2Downloading oss2-2.18.5.tar.gz (283 kB)|████████████████████████████████| 283 kB 6.9 MB/s Collecting aliyun-python-sdk-core>2.13.12Downloading aliyun-python-s…
閱讀更多...
Vmvare—windows中打不開攝像頭

Vmvare—windows中打不開攝像頭

1、檢查本地攝像頭是否能正常打開 設備管理器—查看—顯示隱藏設備—選中照相機—啟動 USB2.0 HD UVC—打開相機查看 2、檢查虛擬機的設置 虛擬機—虛擬機—可移動設備—USB2.0 HD UVC—勾選在狀態欄中顯示 虛擬機—打開windows主機—右小角選中圓圈圖標—勾選連接主機 此時…
閱讀更多...
Android14音頻進階之ADSP調試(七十二)

Android14音頻進階之ADSP調試(七十二)

簡介： CSDN博客專家，專注Android/Linux系統，分享多mic語音方案、音視頻、編解碼等技術，與大家一起成長！ 優質專欄：Audio工程師進階系列【原創干貨持續更新中……】?? 優質專欄：多媒體系統工程師系列【原創干貨持續更新中……】?? 優質視頻課程：AAOS車載系統+AOSP…
閱讀更多...
Java | Leetcode Java題解之第91題解碼方法

Java | Leetcode Java題解之第91題解碼方法

題目&#xff1a; 題解&#xff1a; class Solution {public int numDecodings(String s) {int n s.length();// a f[i-2], b f[i-1], cf[i]int a 0, b 1, c 0;for (int i 1; i < n; i) {c 0;if (s.charAt(i - 1) ! 0) {c b;}if (i > 1 && s.charAt(i …
閱讀更多...
小紅書筆記怎么發瀏覽量高？

小紅書筆記怎么發瀏覽量高？

小紅書筆記發布是有技巧和策略的&#xff0c;為什么有的小紅書筆記瀏覽量那么高&#xff0c;是因為下足了功夫&#xff0c;小紅書筆記怎么發瀏覽量高&#xff1f;今天伯樂網絡傳媒就來給大家揭秘一下。 一、選題與定位 1. 熱門話題選擇 要想提高小紅書筆記的瀏覽量&#xff0…
閱讀更多...
虛擬化技術 使用vSphere Web Client管理ESXi主機

虛擬化技術 使用vSphere Web Client管理ESXi主機

一、實驗內容 通過vSphere Web Client將ESXi主機連接到iSCSI共享存儲通過vSphere Web Client&#xff0c;使用共享存儲創建虛擬機并安裝windows 2008 R2操作系統通過vSphere Web Client&#xff0c;為虛擬機創建快照 二、、實驗主要儀器設備及材料 安裝有64位Windows操作系統…
閱讀更多...
Redis如何避免數據丟失？——AOF

Redis如何避免數據丟失？——AOF

目錄 AOF日志 1. 持久化——命令寫入到AOF文件 寫到用戶緩沖區 AOF的觸發入口函數——propagate 具體的實現邏輯——feedAppendOnlyFile 從用戶緩沖區寫入到AOF文件(磁盤&#xff09; 函數write、fsync、fdatasync Redis的線程池 AOF文件的同步策略 觸發的入口函數——…
閱讀更多...
24.HashMap的擴容機制

24.HashMap的擴容機制

ps&#xff1a;沒看太懂源碼&#xff0c;不確定是否正確... 一、擴容條件 當HashMap中元素的總個數超過&#xff08;threshold&#xff09;閾值&#xff08;數組容量乘以負載因子&#xff09;時&#xff0c;會觸發擴容。默認情況下&#xff0c;&#xff08;capacity&#xff0…
閱讀更多...
JavaScript函數聲明

JavaScript函數聲明

JS函數聲明 JS中的方法,多稱為函數,函數的聲明語法和JAVA中有較大區別 語法1&#xff1a;function 函數名 (參數列表){函數體} 語法2&#xff1a;var 函數名 function (參數列表){函數體} 函數說明 函數沒有權限控制符不用聲明函數的返回值類型,需要返回在函數體中直接return即…
閱讀更多...
UBUNTU下指定執行文件運行時查找庫的路徑

UBUNTU下指定執行文件運行時查找庫的路徑

在Ubuntu下&#xff0c;當指定執行文件時&#xff0c;程序運行時會查找庫文件。通常情況下&#xff0c;程序會在系統默認的庫文件路徑中查找&#xff0c;例如/lib和/usr/lib。 如果需要程序在執行時查找特定路徑下的庫文件&#xff0c;可以通過以下方法實現&#xff1a; 設置環…
閱讀更多...
Gone框架介紹18 - redis 分布式緩存 和 分布式鎖

Gone框架介紹18 - redis 分布式緩存 和 分布式鎖

gone是可以高效開發Web服務的Golang依賴注入框架 github地址&#xff1a;https://github.com/gone-io/gone 文檔地址&#xff1a;https://goner.fun/zh/ 請幫忙在github上點個 ??吧&#xff0c;這對我很重要 &#xff1b;萬分感謝&#xff01;&#xff01; 文章目錄 利用redi…
閱讀更多...
Python | Leetcode Python題解之第92題反轉鏈表II

Python | Leetcode Python題解之第92題反轉鏈表II

題目&#xff1a; 題解&#xff1a; class Solution:def reverseBetween(self, head: ListNode, left: int, right: int) -> ListNode:# 設置 dummyNode 是這一類問題的一般做法dummy_node ListNode(-1)dummy_node.next headpre dummy_nodefor _ in range(left - 1):pre…
閱讀更多...
云計算第十八課

云計算第十八課

目錄操作 移動 改名 批量改名&#xff0c;寫腳本 mv [選項] … 源文件或目錄… 目標文件或目錄 單個文件 移動 或者改名 -f&#xff1a;強制覆蓋&#xff0c;如果目標文件已經存在&#xff0c;則不詢問&#xff0c;直接強制覆蓋&#xff1b; -i&#xff1a;交互移動&#x…
閱讀更多...
零基礎學Java第十四天之抽象類

零基礎學Java第十四天之抽象類

抽象類和抽象類的深入 抽象類 1、理解 抽象類&#xff08;Abstract Class&#xff09;是面向對象編程中的一個重要概念&#xff0c;尤其在像Java、C#和C等編程語言中。抽象類是一種特殊的類&#xff0c;它不能被實例化&#xff08;即不能創建抽象類的對象&#xff09;&#x…
閱讀更多...
鼠標懸浮（hover）時顯示提示框的效果

鼠標懸浮（hover）時顯示提示框的效果

在Vue中&#xff0c;你可以使用多種方法來實現鼠標懸浮&#xff08;hover&#xff09;時顯示提示框的效果。以下是一個簡單的示例&#xff0c;它使用了Vue的指令&#xff08;directive&#xff09;和條件渲染&#xff08;conditional rendering&#xff09;來實現這個功能。 首…
閱讀更多...
最新文章

Copyright @ 2022~2023