目錄

3-1線性回歸

3-2最小二乘解

3-3多元線性回歸

3-4廣義線性模型

3-5對率回歸

3-6對率回歸求解

3-7線性判別分析????????

3-8LDA的多類推廣

3-9多分類學習基本思路

3-10類別不平衡

---

3-1線性回歸

線性模型為什么重要？

人類在考慮問題時，通常很難直接思考非線性的問題

線性模型：試圖學得一個通過屬性的線性組合來進行預測的函數

優點：簡單，基本，可理解性好

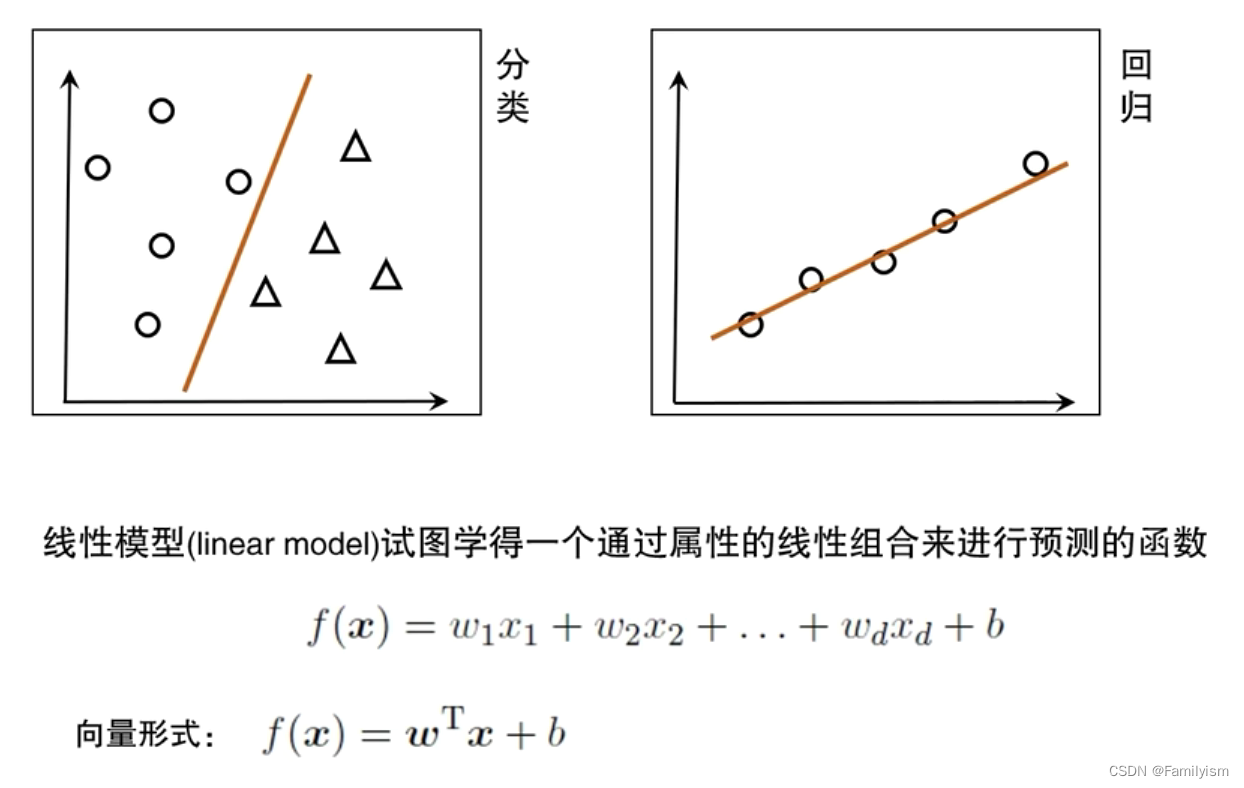
線性回歸

“線性回歸”試圖學得一個線性模型以盡可能地預測實值輸出標記。

均方誤差有非常好的幾何意義，它對應了常用的歐幾里得距離或簡稱“歐式距離”。基于均方誤差最小化來進行模型求解的方法為“最小二乘法”。在線性回歸中，最小二乘法就是試圖找到一條直線，使所有樣本到直線上的歐氏距離之和最小。

3-2最小二乘解

求解w和b使E（w，b）最小化的過程，稱為線性回歸模型的最小二乘“參數估計”

偏導的物理意義表示的是變化率（理解為什么令導數為0）

3-3多元線性回歸

我們把包括兩個或兩個以上自變量的回歸稱為多元線性回歸。

同樣令其為零可得最優解得閉式解，但由于涉及逆矩陣的計算，比單變量情形要復雜一些，需要做簡單的討論。

若存在逆矩陣，直接求解

若不存在，加上不同的歸納偏好，即引入正則化項

3-4廣義線性模型

線性模型雖然簡單，卻有著豐富的變化

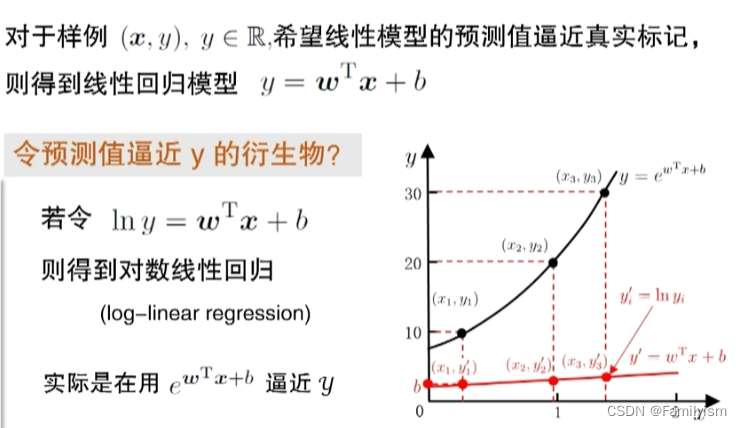
廣義線性模型，線性模型經過操作來逼近y，其中函數g（）被稱為“聯系函數”

3-5對率回歸

考慮“二分類任務”，而線性回歸模型產生的預測值是實值，于是我們需要將實值轉換成0/1值。

最理想的是“單位階躍函數”，但性質不好，我們需要找到替代函數，“對數幾率函數”，簡稱
“對率函數”。

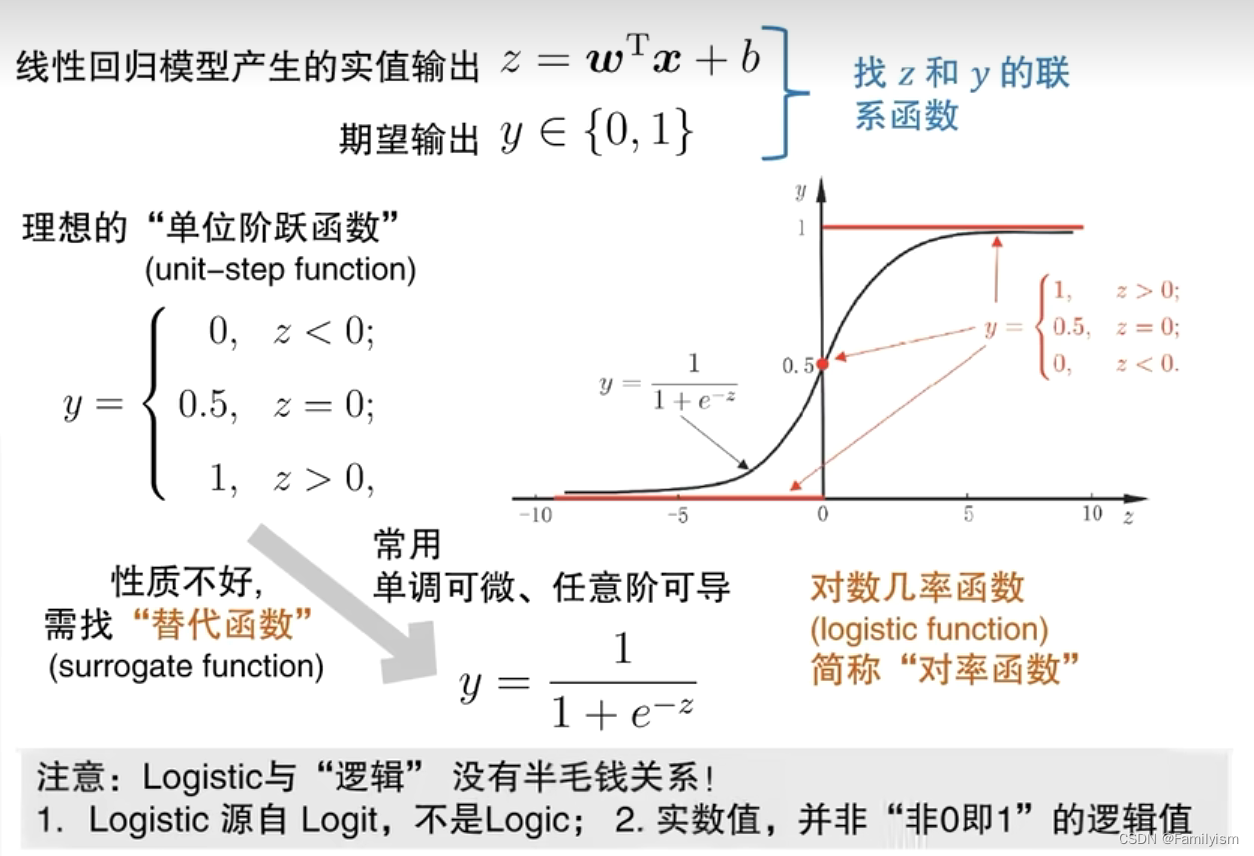
“對數幾率回歸”雖然名字是回歸，但它實際卻是一種分類學習方法

3-6對率回歸求解

求解思路

3-7線性判別分析????????

如何用線性模型直接做分類？線性判別分析簡稱LDA

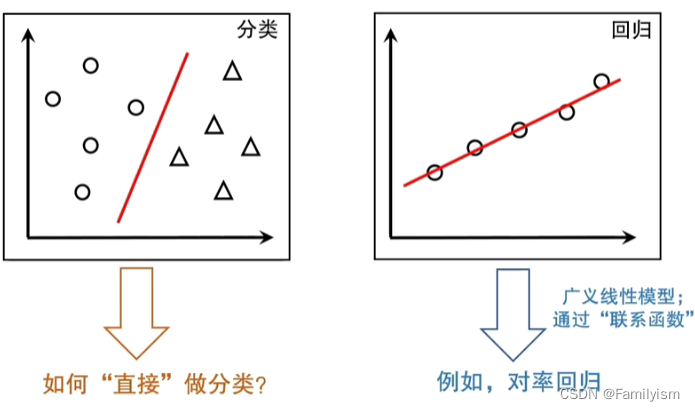
同類盡可能近，異類盡可能遠。

將樣例投影到一條直線，可看作降維技術。

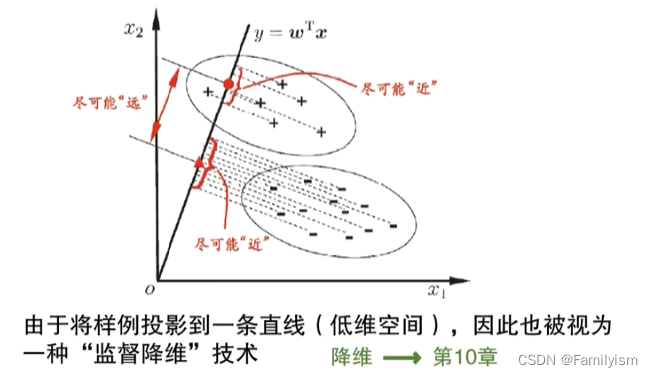
LDA的目標（最大化廣義瑞麗商）

求解過程

3-8LDA的多類推廣

LDA推廣到多類

3-9多分類學習基本思路

現實中常遇到多分類學習任務。有些二分類學習方法可直接推廣到多分類。但在更多情形下，我們是基于一些基本策略，利用二分類學習器來解決多分類問題。

多分類學習的基本思路是“拆分法”。最典型的拆分策略有三種：“一對一”（簡稱“OvO”），“一對其余”（簡稱OvR），“多對多(簡稱MvM)"

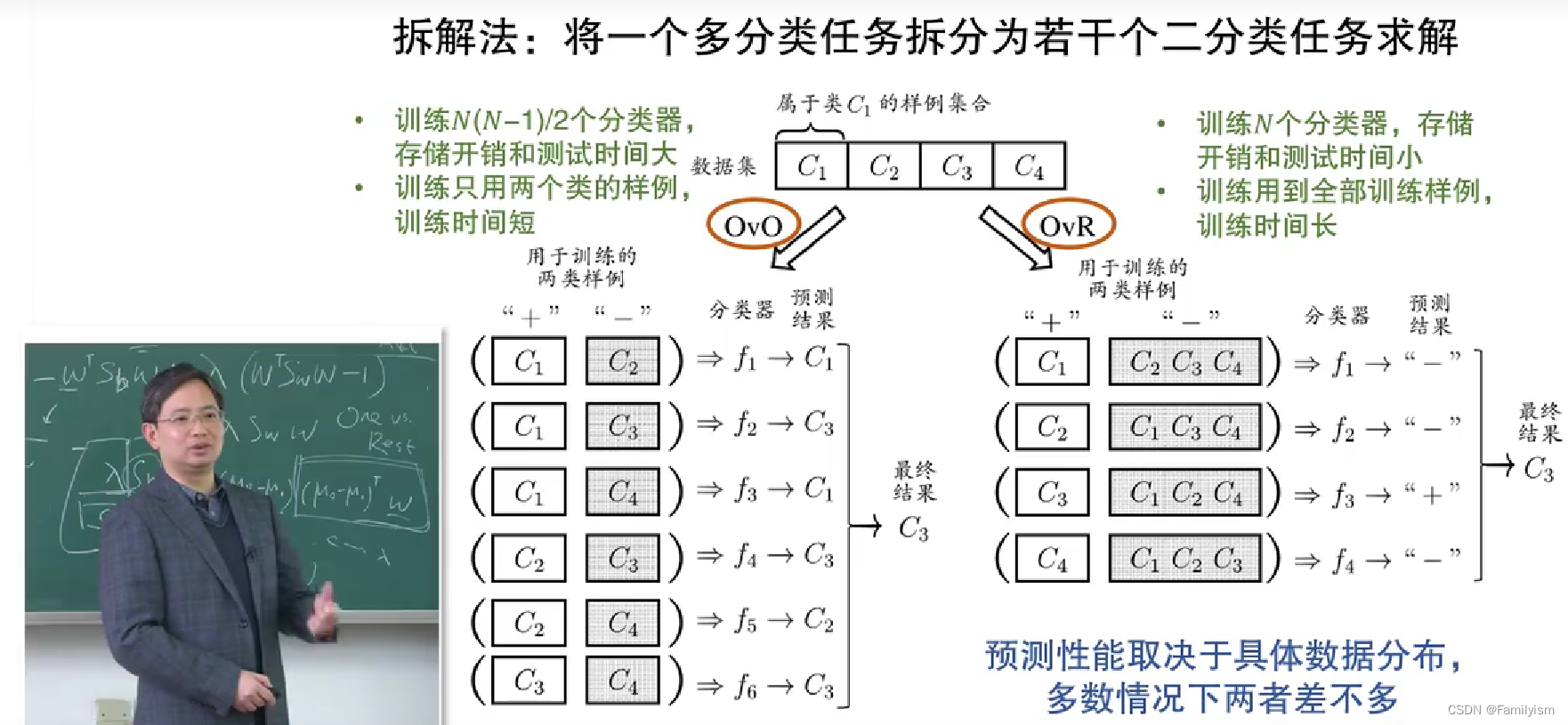
3-10類別不平衡

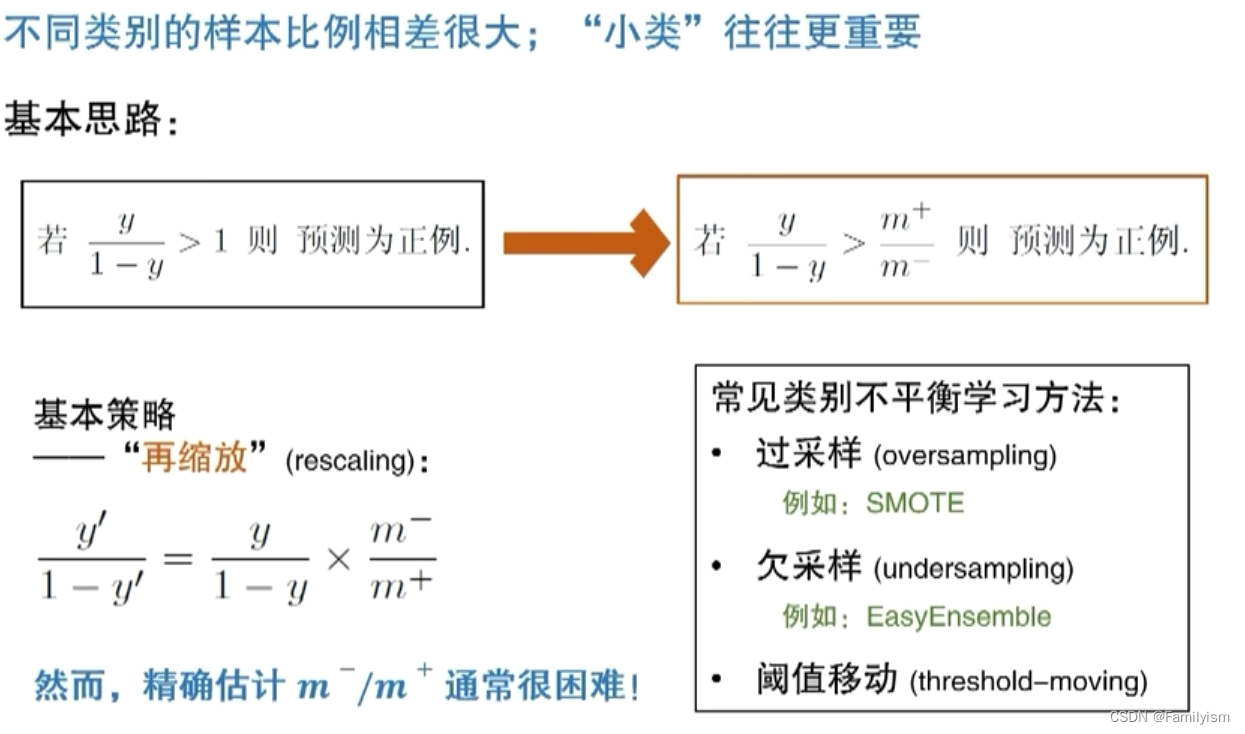
前面介紹的分類學習方法都有一個共同的假設，即不同類別的訓練樣本數目相當。但若不同類別的訓練樣例差距過大，則會對學習過程造成很大的影響。

也不是所有的類別不平衡都要處理，只有當丟掉的小類價值很高時才進行處理。（eg：信用卡檢測）

過采樣：增加小類的采樣，在中間插值

欠采樣：減少大類的采樣，丟棄部分數據

閾值移動：修改閾值