三角函數積分求導公式的巧妙記憶

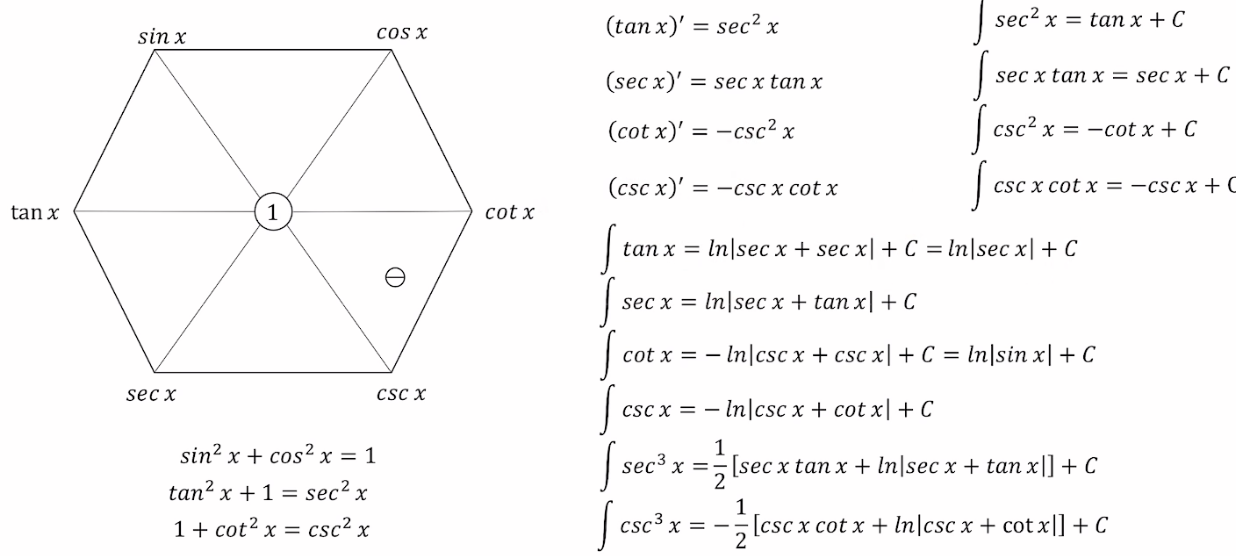
圖像的整體記憶：
上面是sinx cosx
下面也是s開頭，secx，cscx
中間是tanx cotx

解釋說明：
1?? 對角線互為倒數，即sinx對角線是cscx，這樣我們可以更好記住這個六邊形圖像。
2??順時針方向上，某一個三角函數=接下來的兩個三角函數之比，如tanx=sinx/cosx
3??平方和規律，大六邊形由6個小三角形組成，其中的三個倒三角形的上兩個頂點平方和，等于下面那個點的平方
4?? 對三角函數無論是積分還是求導，我們發現規律都是兩個三角函數組合的形式。
中下下，如果是中間的tanx，cotx，他的導數就是，他下面那個三角函數乘于兩次，注意那個帶負號的三角函數分區，他求導和積分要帶負號。
下下中，同理
導相乘，對對和：求導是相乘，積分是加一起。
5?? 記住導數，積分導數互為逆運算，所以不難記住。
6??三次方公式也要記憶，二分之一導+和別忘了csc有負號

重要的說明：

$$\begin{gathered} \ln \left|\sec x+secx\right|+C=\ln \left|2\sec x\right|+C=\ln 2+\ln \left|\sec x\right|=\ln \left|\sec x\right|+C負號 \\ ?\ln \left|\csc x+\csc x\right|+C=?\ln \left|2\csc x\right|+C=?\ln 2+?\ln \left|\csc x\right|=?\ln \left|\csc x\right|+C=\ln \left|sinx\right|+C負號提進去 \\ ?\ln \left|\csc x+\cot x\right|+C=可以把負號提進去，取倒數整理=書上公式=\ln \left|\csc x?\cot x\right|這個記哪個都行 \end{gathered}$$