1.電機模型辨識實驗
1.1 實驗目的
(1)掌握一階系統階躍響應的特點,通過實驗加深對直流電解模型的理解;
(2)掌握系統建模過程中參數的整定,體會參數變化對系統的影響;
(3)熟悉Matlab軟件在計算機控制方面的應用掌握建模擬合曲線的方法。
1.2 實驗原理
????????在設計數字控制系統的控制算法的過程中,往往借助在 Matlab 等仿真軟件中模擬實際系統在特定算法中的工作情況,以便設計和改進控制算法。因此,必須建立被控對象的準確的數學模型,對于參數已知的系統可以通過數學計算產生傳遞函數,而對于參數未知的被控對象可以通過系統辨識來確定其傳遞函數。目前普遍采用的系統辨識的方法主要有階躍響應和沖激響應等。
????????利用階躍響應辨識系統,就是在 t 時刻向系統輸入階躍信號,通過測量系統的響應曲線,反推出系統的傳遞函數參數。例如系統的傳遞函數未知為 W(s),在 t 時刻以前輸入值為 0,在 t 時刻時輸入值變為 1,則系統的輸出與時間的關系為 y(t),上述關系表示為圖2.1。
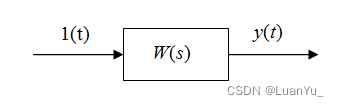
圖 2.1 階躍響應示意圖
????????由于輸入為 1(t)已知,輸出 y(t)通過測量可得,從而可以計算出系統的傳遞函數 W(s)的參數。由于通過階躍響應進行系統辨識的實驗操作和運算簡單,本文以此為手段辨識調速實驗系統中被控對象的傳遞函數。
????????調速系統中的被控對象是一臺直流伺服電機,其額定電壓為 12V,額定電流為0.07A,其內部參數未知,傳遞函數待測。由于該直流電機較小,其內部線圈電感值等參數可忽略,轉速 n 和其他參量的關系可以表示為式(2.1)。

式中 為電樞供電電壓(V),
為電樞電流(A),
為電樞回路總電阻,
為電勢系數。由于電機的電樞供電電壓來自于直流調壓模塊,階躍響應的輸入值由上位機設定轉速占空比表示,故將直流調壓模塊與小型直流電機共同看作無延時一階慣性系統,其傳遞函數可表示為式(2.2)。

????????其中 K 和 T1 為系統中未知的參數值,可見只需要根據階躍響應和輸入階躍值算出 K 和T1 的值即可得到被控對象的傳遞函數。
1.3 實驗過程
????????使用KEIL C51按照操作手冊中介紹的方法建立調速系統辨識實驗工程,名為速度開環,其核心代碼如下所示:
void Port_init()
{P1M1=0x00; //配置P1各個端口的模式P1M0=0x00;
}
void PWM_init(void)
{CCON = 0X00;CH = 0X00;CL = CH;CMOD = 0X02; //TIMER CLOCK RESORCE
}
void PWM0_Setting(unsigned char pwm)
{CCAP0H = 255-pwm;CCAP0L = CCAP0H; CCAPM0 = 0X42; //CCAPMn寄存器的PWMn和ECOMn必須置位CR = 1; //PWM 啟動
}
void ClosePWM0()
{CCAPM0=0;
}
????????將工程編譯生成的speed_open.hex文件在STC ISP軟件中打開,按照操作手冊中介紹的方法把程序下載到單片機中,通過上位機設定轉速占空比。
????????以上準備工作完畢之后,啟動控制過程并觀察速度曲線,當發現電機進入穩態時停止控制過程并保存數據,數據會保存在名data.txt文件中。
????????然后按照實驗操作手冊中關于使用Matlab工具箱進行模型辨識的具體步驟進行辨識,根據三次實驗得到的K平均值和T1 平均值。在 Matlab 中進行一階系統進行階躍響應仿真實驗,具體實驗代碼如下所示,判斷結果是否與仿真吻合。
function [ output_args ] = Untitled2( input_args )
load 234.txt
A = textread('234.txt');
G = tf(1508.976,[0.0199 1]);
x = 0:0.005:7.81;
y = step(G,x);
plot(y,'LineWidth',2);
axis([0 240,0 3500]);
hold on
plot(A,'r')
end
1.4 實驗結果及分析
1.4.1 占空比設為30
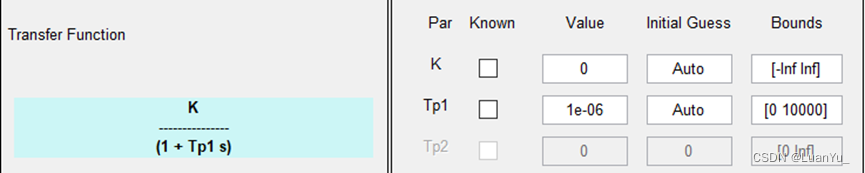
通過辨識結果可知,占空比設為30時,由于占空比過低,導致電機無法正常運行,無法辨識出正確的K值與T1 值。
1.4.2 占空比設為60
(1)辨識結果
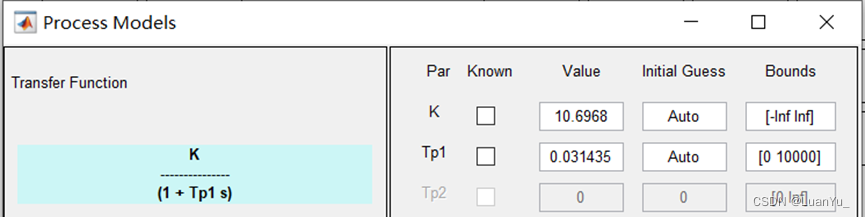


K=11.3931;T1 =0.03517;n=2212
(2)仿真結果與實物結果比較分析

????????通過圖中可以看出,較為平滑的曲線為仿真曲線,帶有鋸齒的曲線為三次實物測試結果,可以看出由于系統的自身誤差,導致三次測試結果有一些差異,但是實物曲線與仿真曲線基本吻合。
1.4.3 占空比設為90
(1)辨識結果


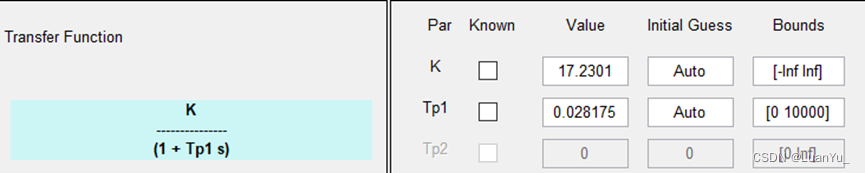
K=16.7408;T1 =0.02764;n=1704
(2)仿真結果與實物結果比較分析
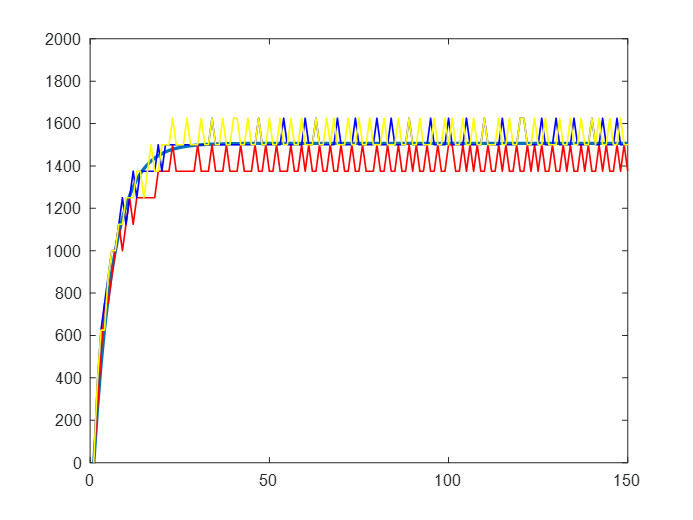
????????通過圖中可以看出,較為平滑的曲線為仿真曲線,帶有鋸齒的曲線為三次實物測試結果,可以看出由于系統的自身誤差,導致三次測試結果有一些差異,但是實物曲線與仿真曲線基本吻合。
1.4.4 占空比設為120
(1)辨識結果



K=19.3626;T1 =0.02588;n=1599
(2)仿真結果與實物結果比較分析
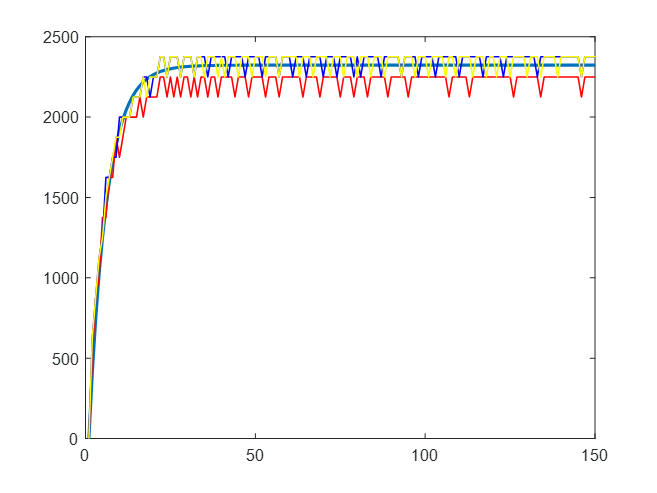
????????通過圖中可以看出,較為平滑的曲線為仿真曲線,帶有鋸齒的曲線為三次實物測試結果,可以看出由于系統的自身誤差,導致三次測試結果有一些差異,且由于占空比較大,實物曲線存在較多飽和部分,但是實物曲線與仿真曲線基本吻合。
1.4.5 占空比設為150
(1)辨識結果



K=20.9127;T1 =0.0255;n=1450
(2)仿真結果與實物結果比較分析
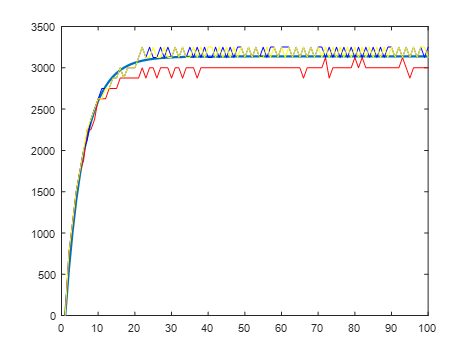
通過圖中可以看出,較為平滑的曲線為仿真曲線,帶有鋸齒的曲線為三次實物測試結果,可以看出由于系統的自身誤差,導致三次測試結果有一些差異,且相比于占空比為120的實物曲線,存在更多的飽和部分,但是實物曲線與仿真曲線基本吻合。
1.4.6 占空比設為180
- 辨識結果

(2)仿真結果與實物結果比較分析
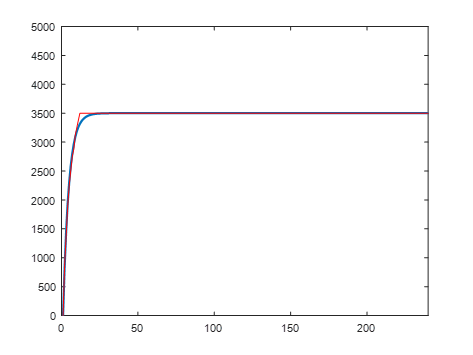
????????由圖象可以看出,電機曲線完全飽和,當電機占空比超過臨界時,轉速穩定在3500r/min,此時實物圖象無法準確表現點擊真實運轉情況,不具有分析性。
1.5 綜合分析
????????隨著電機占空比的增加,辨識出的K值不斷增加,T1 值基本不變,電機穩定轉速不斷增加;當電機占空比低于臨界時,電機不轉;當電機占空比高于臨界時,電機飽和,維持在可測最大轉速。
2.溫度系統模型辨識實驗
2.1 實驗目的
(1)掌握帶純滯后的一階慣性系統的傳遞函數與控制特點;
(2)掌握系統建模過程中參數的整定,體會參數變化對控制系統的影響;
(3)熟悉Matlab軟件在計算機控制方面的應用;
2.2 實驗原理
????????模型辨識的原理速度辨識實驗所述一樣,僅針對于溫控系統的被控對象傳遞函數進行分析。
????????溫控系統中的被控對象是一導熱性良好的銅塊,當設定一個目標溫度值時,通過PWM輸出調節實際溫度向目標溫度靠近,當溫度達到目標值時,會繼續上升一段時間,達到一定閾值才開始下降,因此在控制上存在一定的滯后性。由于加熱片供電電壓來自于直流調壓模塊,階躍響應的輸入值由上位機設定轉速占空比表示,故將直流調壓模塊與加熱銅塊共同看作具有純滯后的一階慣性系統,其傳遞函數可表示
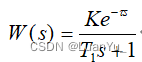
????????其中 K、T1、τ為系統中未知的參數值,可見只需要根據階躍響應和輸入階躍值算出K、T1、τ的值即可得到被控對象的傳遞函數。
2.3 實驗過程
????????使用KEIL C51按照操作手冊中介紹的方法建立溫控速系統辨識實驗工程,名為溫度開環,其核心代碼如下所示:
void main() //主函數
{Port_Init();Heater_Init();TM1638_Init();InitPWM();EA=1;UART_init(19200);ES=1; while(Start_Flag != 1);Start_Flag = 0; ConfigT1M1();ENHeater();SetPWM1(set_value);display(0000);while(1){ if(timer1flag){timer1flag=0;PreReadTemp();TempShow = ReadTemp();SendData(TempShow);display(TempShow);}if(Stop_Flag){Stop_Flag = 0;ClosePWM1();Heater_Init();}if(Reset_Flag){ISP_CONTR=0X20; }}
}
//驅動代碼
void InitPWM(void)
{CCON&=0X00; CH=0X00;CL=CH;CMOD=0X02;
}
void SetPWM1(unsigned char pwm)
{CCAP1H = 255-pwm;CCAP1L = CCAP1H;CCAPM1 = 0X42;CR = 1;
}
void ClosePWM1()
{CCAPM1=0;
}
void Port_Init()
{P1M1=0x00;P1M0=0x00;
}
????????程序編譯無誤后,將wd_open.hex通過STC ISP下載工具下載到單片機中,通過上位機設定占空比。
????????啟動控制過程并觀察溫度曲線,當發現溫度趨于平穩時停止控制過程并保存數據,數據會保存在名為data.txt文件中。
????????然后按照實驗操作手冊中關于使用Matlab工具箱進行模型辨識的具體步驟進行辨識,根據得到的K值、值、
值。在 Matlab 中進行一階系統進行階躍響應仿真實驗,具體實驗代碼如下所示,判斷結果是否與仿真吻合。
load 456.txt %數據名
A = textread('456.txt');
A = A(:,1)-22.87;
num = [0,6.521];
den = [1258.566,1];
G = tf(num,den,'InputDelay',21.122);
x = 0:1:2340;
y = step(G,x);
plot(y,'LineWidth',2);
axis([0 3200,0 40]);
hold on
plot(A,'r')
2.4 實驗結果及分析
(1)辨識結果
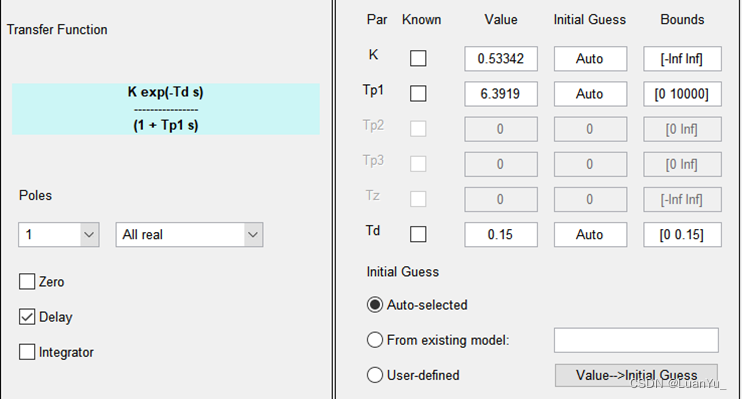
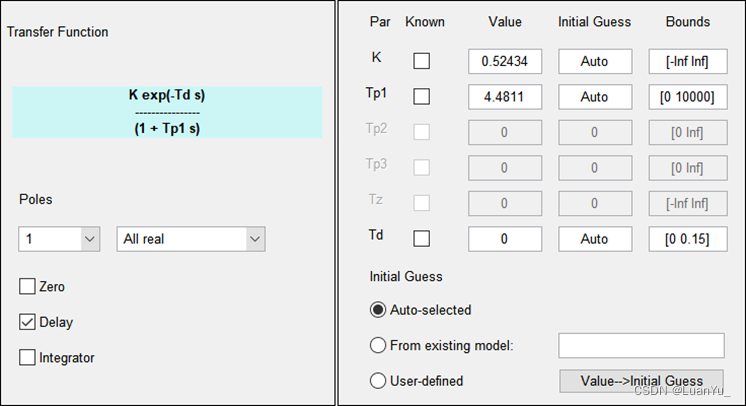
![]()
(2)仿真結果與實物結果比較分析
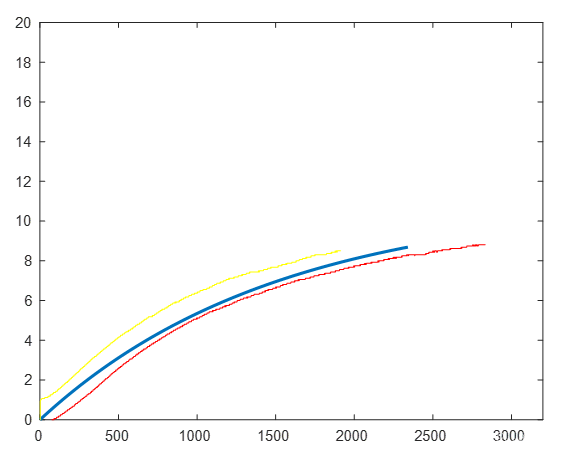
????????本次實驗,我們幾乎沒有辨識出延時環節,正常由于儀器溫度升到室溫有一定的時間,因此對于溫度辨識實驗應該有10s-20s的延時環節,但由于我們在做實驗時,并不是從加熱開始進行測量,而是在儀器已經加熱一段時間后才開始進行測量,此時儀器溫度已經接近室溫,在第二次實驗降溫時也沒有降到室溫以下,因此在辨識中,沒有較為明顯的延時環節。從圖中看出兩次實物結果有一定差異,可能由兩次起始溫度不一樣和系統自身誤差造成,但仿真曲線與實物曲線基本吻合,總體來說實驗成功。
3.電機速度PID實驗
3.1 實驗目的
(1)通過實驗了解調速控制系統的硬件組成,以及各個單元的作用;
(2)掌握PID各項參數的作用;
(3)掌握調速系統中PID運算的參數整定;
(4)初步掌握閉環系統的基本調試方法;
3.2 實驗原理
????????當被控對象的結構和參數不能完全掌握,或得不到精確的數學模型時,控制理論的其它技術難以采用時,系統控制器的結構和參數必須依靠經驗和現場調試來確定,這時應用PID控制技術最為方便。即當我們不完全了解一個系統和被控對象,或不能通過有效的測量手段來獲得系統參數時,最適合用PID控制技術。PID控制器就是根據系統的誤差,利用比例、積分、微分計算出控制量進行控制的,即調節器的輸出與輸入是比例—積分—微分的關系。
????????在計算機控制系統中,使用數字PID,將上式離散化,寫成差分方程:

3.3 實驗過程
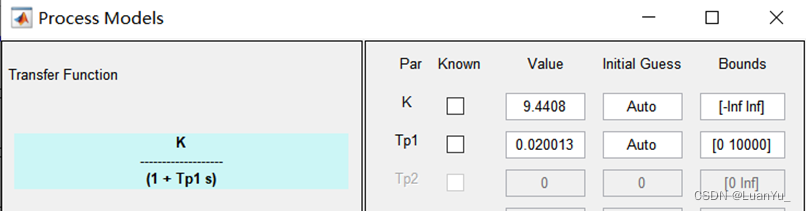
(1)實驗代碼
function [ output_args ] = untitled2( input_args )
load SD.txt
A = textread('SD.txt');
G = tf(1132.896,[0.020013 1]);
x = 0:0.005:7.215;
y = step(G,x);
plot(y,'LineWidth',2);
axis([0 50,0 1200]);
hold on
plot(A,'r','LineWidth',1)
end
(2)運行結果

(3)實驗代碼
function [ output_args ] = untitled2( input_args )
load SDPID.txt
load SD240.txt
W = textread('SDPID.txt');
A = textread('SD240.txt');
axis([0 100,0 1500]);
hold on
plot(W,'b','LineWidth',1)
plot(A,'r','LineWidth',1)
end
(4)運行結果
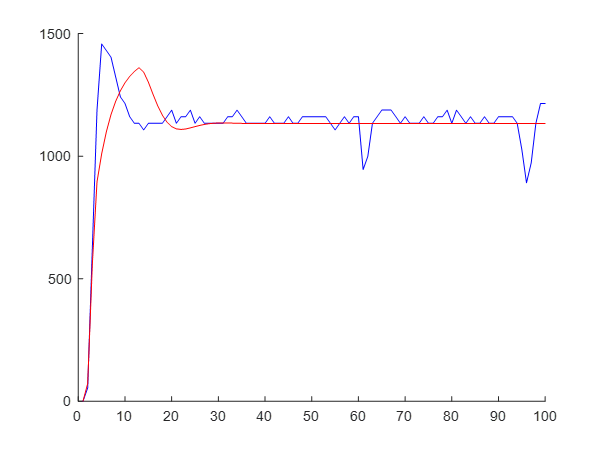
3.4 思考與解答
1、什么是一般PID控制以及一般PID算法;
答:PID算法的參數調試是指通過調整控制參數(比例增益、積分增益/時間、微分增益/時間)讓系統達到最佳的控制效果。
2、說明位置式PID和增量式PID的區別。
答:(1)位置式PID控制的輸出與整個過去的狀態有關,用到了誤差的累加值;而增量式PID的輸出只與當前拍和前兩拍的誤差有關,因此位置式PID控制的累積誤差相對更大;
(2)增量式PID控制輸出的是控制量增量,并無積分作用,因此該方法適用于執行機構帶積分部件的對象,如步進電機等,而位置式PID適用于執行機構不帶積分部件的對象,如電液伺服閥。
(3)由于增量式PID輸出的是控制量增量,如果計算機出現故障,誤動作影響較小,而執行機構本身有記憶功能,可仍保持原位,不會嚴重影響系統的工作,而位置式的輸出直接對應對象的輸出,因此對系統影響較大。
4.溫控系統PID實驗
4.1 實驗目的
(1) 通過實驗了解溫度控制系統的硬件組成,各個單元的作用以及信號量在系統中的傳遞過程;
(2) 用Keil建立工程,編寫PID控制算法;
(3) 掌握PID各項參數的作用;
(4) 初步掌握閉環系統的基本調試方法。
4.2 理論分析
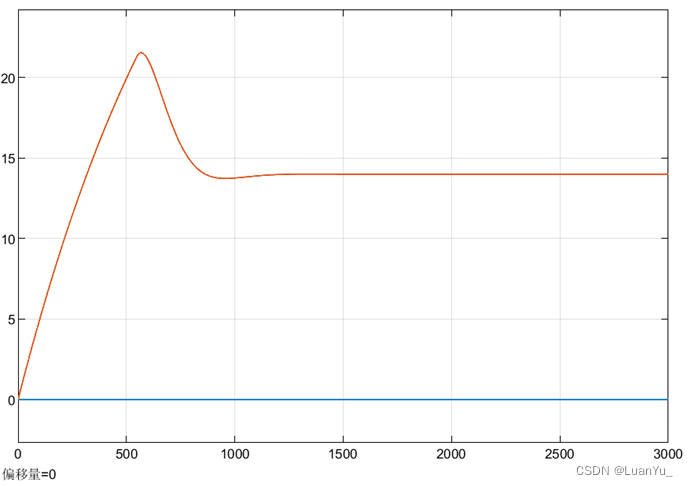
P=70,I=0.65,D=0.2
4.3 實驗過程
(1)Matlab代碼
function [ output_args ] = untitled2( input_args )
load WD.txt
A = textread('WD.txt');
plot(A,'r','LineWidth',1)
end
(2)運行結果
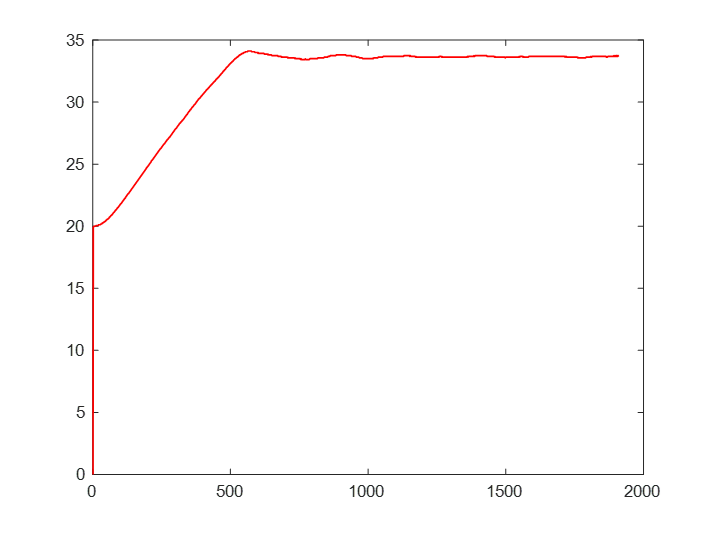
4.4 比較結果
????????通過理論與實際對比分析可以看出,理論與實際之間有些區別,可能是由于外界空氣流動de那個因素干擾導致
5.電機速度最小拍實驗
5.1 實驗目的
(1)掌握最小拍控制器的設計方法;
(2)比較最小拍控制器和經典PID控制器的控制效果;
(3)無紋波和有紋波的在設計上的區別。
5.2 理論分析
(1)控制器設計

a. 求G(z)
>> s = tf('s');
>> Gc = (19.156/(0.025649*s+1));
>> c2d(Gc,0.01,'z')
ans =
??? 6.185
? ----------
? z - 0.6771
采樣時間: 0.01 seconds
離散時間傳遞函數。
b. 求D(z)

(2)建立simulink模型:
a. 未加限幅

????????輸出波形如下,同時將生成的數據導入到工作區方便后續與實物數據進行比較。
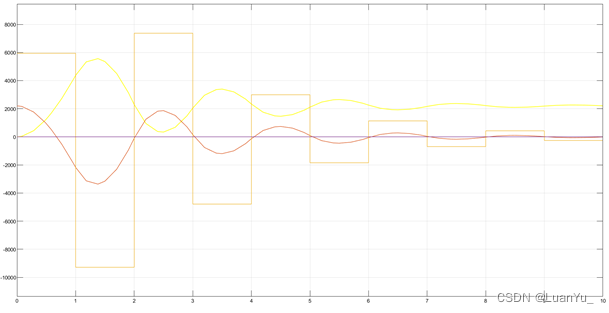
b.?加入正負250限幅后

5.3 實驗過程
????????在實驗中我們利用占空比為120的模型進行識別,利用matlab工具識別出被控對象為:
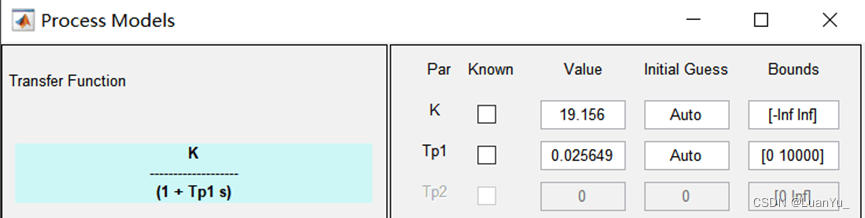
????????最小拍核心代碼如下:
float ZXP_Control(float refspeed,float realspeed
{ int duty_err;err = refspeed - realspeed;duty_err = duty_err_last + err / 6.14 - err_last_1 / 6.14 * 0.773;duty_err_last = duty_err;err_last_1 = err;if(duty_err < 0) duty_err = 0;if(duty_err + 39 > 250) //39是考慮電機死區的因素return 250;else return duty_err + 39;
}
5.4 比較結果
(1)Matlab代碼如下
function [ output_args ] = untitled2( input_args )
load SD120.txt
load ZXP.txt
load YXP.txtA = textread('SD120.txt');
W= textread('ZXP.txt');
Q= textread('YXP.txt');
G = tf(2298.72,[0.025649 1]);
x = 0:0.005:5.48;
y = step(G,x);
plot(y,'LineWidth',2);
axis([0 100,0 3500]);
hold on
plot(A,'r','LineWidth',1)
plot(W,'b','LineWidth',1)
plot(Q,'g','LineWidth',1)
end
(2)運行結果
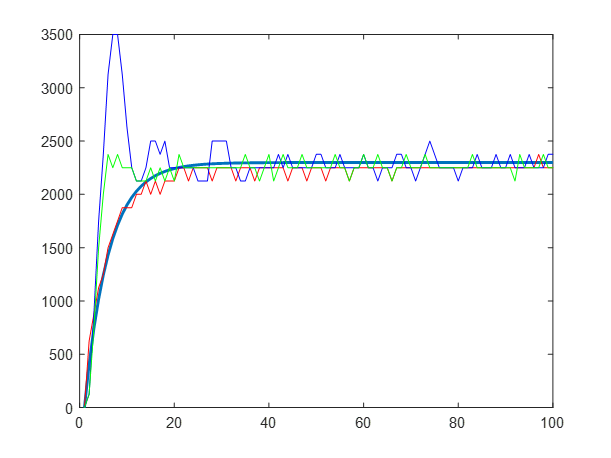
(3)結果分析
????????通過實驗與仿真結果可以看出實驗與仿真結果基本吻合,實驗成功。
5.5?思考與解答
1、最小拍設計的要求是什么?
答:閉環控制系統在最少的采樣周期內達到穩定,且系統在采樣點的輸出能夠準確地跟蹤輸入信號,不存在穩態誤差。
2、最小拍控制器局限性及如何解決?
答:局限性:
(1)最小拍控制系統的輸出在采樣點之間可能存在紋波
(2)最小拍控制系統對各種典型輸入函數的適應性差
(3)最小拍控制系統對被控對象的模型參數變化敏感
解決方法:可以通過最小拍無紋波控制器的設計解決問題1;針對問題23,只有在不同被控對象中,不斷設計控制器來解決。
3、仿真和實際的結果存在一定的差異,簡述存在的差異并分析原因。
答:實際結果在初始時會突變,可能是因為電機老化等外部因素,并由于外界干擾,實驗結果數據有波動,而仿真結果則是在完全理想情況下,無波動。









使用別人的項目與gradle包并運行項目)









