本篇文章Master Hyperparameter Tuning in Machine Learning適合希望深入了解超參數調優的讀者。文章的亮點在于介紹了多種調優方法,如手動搜索、網格搜索、隨機搜索、貝葉斯優化和元啟發式算法,并通過實際案例展示了這些方法在復雜模型(如CNN)和簡單模型(如SVM)中的應用效果。
文章目錄
- 1. 引言
- 2. 什么是超參數調優
- 3. 手動搜索
- 3.1 模擬
- 3.1.1 構建和評估模型
- 3.1.2 準備數據集
- 3.1.3 搜索超參數
- 3.1.4 結果
- 4. 網格搜索
- 4.1 搜索空間
- 4.2 模擬
- 4.3 結果
- 5. 隨機搜索
- 5.1 搜索空間
- 5.2 模擬
- 5.3 結果
- 6. 貝葉斯優化
- 6.1 選擇代理模型
- 6.2 高斯過程的數學形式
- 6.3 在搜索空間中尋找下一個評估點
- 6.4 搜索空間
- 6.5 模擬
- 6.6 結果
- 7. 元啟發式算法
- 7.1 元啟發式算法如何工作
- 7.2 元啟發式算法的類型
- 7.3 搜索空間
- 7.4 模擬
- 7.4.1 步驟 1. 初始化:創建種群
- 7.4.2 步驟 2. 評估:計算適應度分數
- 7.4.3 步驟 3: 迭代
- 7.4.4 步驟 4 & 5: 選擇最佳參數
- 7.5 結果
- 8. 泛化能力和時間效率的最終評估
- 8.1 泛化能力
- 8.2 時間效率
- 9. 針對表格數據上訓練的簡單模型
- 9.1 表格數據
- 9.2 搜索空間
- 9.3 評估模型
- 9.4 結果
- 9.4.1 手動搜索
- 9.4.2 網格搜索
- 9.4.3 隨機搜索
- 9.4.4 貝葉斯優化 (Scikit-Optimize)
- 9.4.5 遺傳算法
- 10. 結論

1. 引言
超參數調優是影響傳統機器學習和深度學習模型性能的關鍵步驟。
雖然存在許多技術,但選擇最佳調優方法取決于以下因素:
- 模型復雜性:更復雜的模型自然會導致更大的搜索空間。
- 數據復雜性:數據集的特性會影響調優難度。
- 對模型的熟悉程度:我們對模型行為的理解可以指導調優選擇并定義搜索空間。
在本文中,我將演示在不同場景下,如何使用五種關鍵調優方法來調優模型,包括:
- 手動搜索 (Manual Search)
- 網格搜索 (Grid Search)
- 隨機搜索 (Random Search)
- 貝葉斯優化 (Bayesian Optimization)
- 元啟發式算法 (Metaheuristic Algorithm)
這些方法將應用于處理高維圖像數據的卷積神經網絡 (CNN) 和處理簡單表格數據的核支持向量機 (Kernel SVM)。
2. 什么是超參數調優
超參數調優是一個技術過程,用于在模型訓練之前調整機器學習模型的配置設置,這些設置被稱為超參數。
與訓練期間學習到的模型參數(例如,權重和偏差)不同,超參數不是從數據中估計出來的,并且大多數機器學習模型都依賴于許多超參數。
例如,在卷積神經網絡 (CNN) 的情況下,輸入層形狀、卷積層設置(如濾波器數量、濾波器大小、步長、填充)、輸出層大小以及編譯器設置(如優化器、損失函數和評估指標)都確實是超參數。
因此,調優這些超參數是提高模型性能同時實現計算效率的關鍵步驟。
存在各種方法來處理這個調優過程。主要的方法,按復雜性和智能程度排序,包括:
- 手動搜索 (Manual Search)
- 網格搜索 (Grid Search)
- 隨機搜索 (Random Search)
- 貝葉斯優化 (Bayesian Optimization)
- 元啟發式算法 (Metaheuristic Algorithm)
每種方法在計算成本、搜索效率以及找到真正最優配置(全局最優)的可能性之間提供了不同的權衡。
那么,讓我們看看如何利用每個方法來解決一個真實世界的案例。
真實世界案例:工廠主的挑戰
讓我們想象一個場景,一位工廠主正在對用于高精度裝配的小齒輪進行檢查。

手動目視檢查既慢又容易出錯。
因此,工廠主計劃開發一個基于 AI 的檢查系統,使用 CNN 執行回歸任務,從高分辨率相機捕獲的圖像中估計連續的半徑值。
目標
我們這個項目的最終目標是找到 CNN 的最佳超參數組合并最小化泛化誤差。
我將使用平均絕對誤差 (MAE) 作為評估指標,因為它可以評估像素的精確度。
實際上,可以根據項目的目標設置適當的指標。
現在,讓我們看看每種方法是如何工作的。
3. 手動搜索
手動搜索是最基本的方法,人類手動嘗試不同的超參數值,訓練模型,并評估其性能。
它通常由直覺、領域專業知識和先驗經驗驅動。
最佳使用場景:
- 初步探索:剛開始使用新模型或數據集,需要大致了解超參數的影響。
- 小搜索空間:適用于超參數很少或取值范圍很窄的模型。
- 有限的計算資源:計算能力非常有限,只能負擔少量試驗。
局限性:
- 極其耗時,高度主觀。
- 對于復雜模型很少能找到真正最優的解決方案。
3.1 模擬
由于這是我們的第一次嘗試,我將設置數據集以及用于評估模型的函數。
3.1.1 構建和評估模型
build_cnn_model 函數通過接受 hparams(一個超參數集合字典)作為參數來構建各種模式的 CNN。所有模型默認都將 MAE 作為其評估指標。
然后,evaluate_model 函數使用驗證數據集構建、訓練和評估每個模型。此函數返回訓練好的模型和關鍵的評估指標:
eval_count:在調優過程中訓練和評估的不同超參數集的數量,total_time:從搜索開始到結束的總時間(秒),以及mae:搜索期間生成的最佳 MAE 分數。
import tensorflow as tf
from tensorflow import keras
from keras import models, layers, optimizers, metrics, losses, backend, callbacksdef build_cnn_model(hparams: dict, input_shape=X_train.shape[1:]): inputs = layers.Input(shape=input_shape)x = layers.Conv2D(hparams['filters_0'], (3, 3), activation='relu')(inputs) if hparams.get('batch_norm_0', False): x = layers.BatchNormalization()(x) x = layers.MaxPooling2D((2, 2))(x)for i in range(1, hparams.get('num_conv_layers', 1)): if f'filters_{i}' in hparams: x = layers.Conv2D(hparams.get(f'filters_{i}', 16), (3, 3), activation='relu')(x) if hparams.get(f'batch_norm_{i}', False): x = layers.BatchNormalization()(x) x = layers.MaxPooling2D((2, 2))(x) x = layers.Flatten()(x) x = layers.Dense(hparams['dense_units'], activation='relu')(x) if hparams['dropout'] > 0: x = layers.Dropout(hparams['dropout'])(x)outputs = layers.Dense(1)(x)model = models.Model(inputs=inputs, outputs=outputs) model.compile( optimizer=optimizers.Adam(learning_rate=hparams['learning_rate']), loss=losses.MeanSquaredError(), metrics=[metrics.MeanAbsoluteError(name='mae')] ) return modeldef evaluate_model(hparams: dict, eval_count: int = 0, total_time: float = 0.0) -> tuple: eval_count += 1 start_time = time.time()model = build_cnn_model(hparams)early_stopping = callbacks.EarlyStopping( monitor='val_mae', patience=5, restore_best_weights=True, verbose=1 ) model.fit( X_train, y_train, epochs=hparams.get('epochs', 100), validation_data=(X_val, y_val), batch_size=16, callbacks=[early_stopping], verbose=0 )_, mae = model.evaluate(X_val, y_val, verbose=0)end_time = time.time() total_time += (end_time - start_time)backend.clear_session()return eval_count, total_time, mae, model
注意:由于其復雜性,CNN 很容易在訓練數據集上過擬合。在回調中添加早停設置至關重要。
3.1.2 準備數據集
我從 1,000 張合成的 28 × 28 像素圖像創建了訓練、驗證和測試數據集:
import numpy as np
from sklearn.model_selection import train_test_split
import numpy as np
from sklearn.model_selection import train_test_splitimg_height, img_width = 28, 28
min_radius, max_radius = 1, 10
n_samples = 1000
images, targets = [], []for i in range(n_samples): img, target = generate_image_and_target(img_height, img_width, min_radius, max_radius, noise_level) images.append(img) targets.append(target)X = np.array(images)
X = X.reshape(n_samples, img_height, img_width, 1)
y = np.array(targets)X_tv, X_test, y_tv, y_test = train_test_split(X, y, test_size=200, random_state=42, shuffle=True)
X_train, X_val, y_train, y_val = train_test_split(X_tv, y_tv, test_size=200, random_state=42, shuffle=True)print(X_train.shape, y_train.shape, X_val.shape, y_val.shape, X_test.shape, y_test.shape)
(600, 28, 28, 1) (600,) (200, 28, 28, 1) (200,) (200, 28, 28, 1) (200,)
現在,讓我們開始手動搜索。
3.1.3 搜索超參數
我隨機定義了三種超參數組合,并選擇了 MAE 最好的一個:
hparam_options = [ { 'num_conv_layers': 1, 'filters_0': 16, 'batch_norm_0': False, 'dense_units': 16, 'dropout': 0.0, 'learning_rate': 0.001, 'epochs': 50 }, { 'num_conv_layers': 1, 'filters_0': 16, 'batch_norm_0': False, 'dense_units': 16, 'dropout': 0.0, 'learning_rate': 0.001, 'epochs': 200 }, { 'num_conv_layers': 2, 'filters_0': 32, 'batch_norm_0': True, 'filters_1': 64, 'batch_norm_1': True, 'dense_units': 32, 'dropout': 0.1, 'learning_rate': 0.001, 'epochs': 100 },
]eval_count = 0
total_time = 0.0
best_mae = float('inf')
best_hparams = None
best_model = Nonefor item in hparam_options: eval_count_returned, total_time_returned, current_mae, model = evaluate_model(hparams=item) eval_count += eval_count_returned total_time += total_time_returnedif current_mae < best_mae: best_mae = current_mae best_hparams = item best_model = modelreturn best_mae, eval_count, total_time, best_hparams, best_model
3.1.4 結果
- 最佳 MAE:0.3663 像素(占總范圍的 4.07%)
- 執行時間:4.9146 秒
- 評估總數:3
- 最佳超參數集:
num_conv_layers: 1, filters_0: 16, batch_norm_0: False, dense_units: 16, dropout: 0.0, learning_rate: 0.001, epochs: 200
hparam_options 中的第二個選項被證明是最好的,MAE 為 0.3663 像素。
考慮到目標半徑范圍在 1 到 10 之間,預測誤差約為總范圍的 4.07% ([0.3663 / (10 - 1) \approx 0.04070])。
這將作為我的閾值。
4. 網格搜索
網格搜索系統地探索預定義、離散值集合(網格)內的所有可能的超參數組合。
例如,如果我們將學習率定義為在 [0.01, 0.001] 處測試,批量大小定義為在 [32, 64] 處測試,網格搜索將測試所有四種組合:[0.01/32, 0.01/64, 0.001/32, 0.001/64]。
最佳使用場景:
- 明確定義的超參數空間:可以根據領域專業知識或先驗經驗,以合理的方式設置適度的超參數選項范圍進行測試。
- 需要窮盡搜索:需要絕對確定在搜索空間內找到最佳組合。
- 可審計性:需要一個徹底且可復現的搜索過程,以用于合規性或理解。
- 充足的計算資源:可以獲得足夠的計算能力來探索搜索空間中的每個組合。
局限性:
- 當超參數數量及其選項增加時(例如,設置 5 個選項 x 10 個超參數 = 50 個模型需要訓練和評估),計算成本會迅速變得昂貴。
- 容易受到維度詛咒的影響。
4.1 搜索空間
網格搜索在其窮盡搜索的努力下,在較小的搜索空間中會更有效。使用過大的搜索空間可能導致耗時的過程。
因此,根據手動搜索中表現最佳的超參數,我定義了一個包含 36 種離散組合的小型搜索空間:
hparams_options = { 'num_conv_layers': [1], 'filters_0': [16, 32], 'batch_norm_0': [False], 'dense_units': [16, 32, 64], 'dropout': [0.0, 0.1, 0.2], 'learning_rate': [0.001, 0.0001], 'epochs': [200],
}
4.2 模擬
我構建、訓練并評估了 36 種 CNN 模式,并選擇了 MAE 最好的一個:
from itertools import productall_combinations_list = []
eval_count = 0
total_time = 0.0
best_mae = float('inf')
best_hparams = None
best_model = Nonefor num_conv in hparams_options['num_conv_layers']: dynamic_filters_bn_combinations = list( product( *(hparams_options[f'filters_{i}'] for i in range(num_conv)), *(hparams_options[f'batch_norm_{i}'] for i in range(num_conv)) ) ) base_combos = product( hparams_options['learning_rate'], hparams_options['epochs'], hparams_options['dense_units'], hparams_options['dropout'] )for base_combo in base_combos: for dynamic_combo in dynamic_filters_bn_combinations: hparam_set = { 'learning_rate': base_combo[0], 'epochs': base_combo[1], 'num_conv_layers': num_conv, 'dense_units': base_combo[2], 'dropout': base_combo[3] } filter_values = dynamic_combo[:num_conv] for i in range(num_conv): hparam_set[f'filters_{i}'] = filter_values[i] all_combinations_list.append(hparam_set)for hparams in all_combinations_list: eval_count_returned, total_time_returned, current_mae, model = evaluate_model(hparams=hparams) eval_count += eval_count_returned total_time += total_time_returnedif current_mae < best_mae: best_mae = current_mae best_hparams = hparams best_model = modelreturn best_mae, eval_count, total_time, best_hparams, best_model
4.3 結果
- 最佳 MAE:0.2675 像素(2.97% 誤差范圍)
- 執行時間:124.7468 秒
- 評估總數:36(測試了所有組合)
- 最佳超參數集:
num_conv_layers: 1, dense_units: 64, dropout: 0.0, filters_0: 16, learning_rate: 0.0001, epochs: 200
網格搜索實現了 2.97% 的誤差范圍,顯著優于手動搜索(4.07%)。
執行耗時 125 秒(大約 2 分鐘)。
除了狹窄的搜索空間之外,早停在這里也發揮了關鍵作用,一旦誤差下降變得微不足道,它就會停止不必要的訓練周期,從而節省搜索時間。
由于其細致的方法,搜索結果顯示了所定義搜索空間的全局最優解。
然而,擴大搜索空間和放寬正則化(早停設置)可能會找到不同的最優解,但會花費更多時間。
5. 隨機搜索
隨機搜索不是窮盡地檢查每個組合,而是從指定的搜索空間中隨機抽樣固定數量的超參數組合。
搜索空間可以是連續的或離散的。這意味著超參數可以在給定范圍內取任何實數值,而無需預定義的值(例如,學習率 = 0.012445 而不是 0.01)。
最佳使用場景:
- 大型超參數空間:當超參數數量或其范圍對于網格搜索來說過于龐大時。
- 效率高于窮盡性:需要快速獲得一個合理好的解決方案,特別是當只有少數超參數真正影響性能時。
- 發現重要超參數:研究表明,在相同的計算預算下,隨機搜索通常比網格搜索找到更好的結果,因為它更有可能探索廣泛不同的值。
局限性:
- 不能保證找到全局最優解,因為它依賴于隨機抽樣。
- 解決方案的質量取決于迭代次數和抽樣的隨機性。
5.1 搜索空間
當它可以從大型搜索空間中盡可能隨機地選擇選項時,隨機搜索表現最佳。
為了利用這一能力,我設置了一個極其龐大的搜索空間,包含廣泛的值范圍,以便它也可以生成隨機連續值。
hparams_options = { 'num_conv_layers': [1, 2, 3, 4], 'filters_0': [16, 32, 48, 64], 'filters_1': [16, 32, 48, 64], 'filters_2': [16, 32, 48, 64], 'filters_3': [16, 32, 48, 64], 'batch_norm_0': [True, False], 'batch_norm_1': [True, False], 'batch_norm_2': [True, False], 'batch_norm_3': [True, False], 'dense_units': [32, 64, 96, 128], 'epochs': [i for i in range(100, 1001)]'dropout': [0.0, 0.5], 'learning_rate': [0.1, 0.0001]
}
5.2 模擬
即使在相同的搜索空間內,隨機搜索的結果在不同試驗之間也會有所不同,因為它探索的是超參數的隨機子集。
為了使結果標準化,我進行了五次試驗,每次從搜索空間中隨機選擇了 50 種組合,并記錄了最佳和平均結果。
在實踐中,我們需要在進行大量試驗以找到絕對全局最優解和限制耗時過程以獲得一個合理好的次優解之間取得平衡。
eval_count = 0
total_time = 0.0best_mae = float('inf')
best_hparams = None
best_model = Nonefor _ in range(n_iterations): hparams = dict()hparams['num_conv_layers'] = random.choice(hparams_options['num_conv_layers']) for i in range(hparams['num_conv_layers']): hparams[f'filters_{i}'] = random.choice(hparams_options[f'filters_{i}']) hparams[f'batch_norm_{i}'] = random.choice(hparams_options[f'batch_norm_{i}']) hparams['dense_units'] = random.choice(hparams_options['dense_units']) hparams['epochs'] = random.choice(hparams_options['epochs'])hparams['learning_rate'] = random.uniform(hparams_options['learning_rate'][0], hparams_options['learning_rate'][-1]) hparams['dropout'] = random.uniform(hparams_options['dropout'][0], hparams_options['dropout'][-1])eval_count_returned, total_time_returned, current_mae, model = evaluate_model(hparams=hparams) eval_count += eval_count_returned total_time += total_time_returnedif current_mae < best_mae: best_mae = current_mae best_hparams = hparams best_model = modelreturn best_mae, eval_count, total_time, best_hparams, best_model
5.3 結果
在五次試驗中,隨機搜索平均實現了 2.48% 的誤差范圍,優于網格搜索的 2.97%。
搜索花費了 **216 秒(約 3.5 分鐘)**來完成 50 次 CNN 模式測試;由于其龐大的搜索空間,速度略慢于網格搜索。
這個結果表明,隨機搜索在速度和性能之間取得了良好的平衡,性能或時間上只有很小的折衷。
通過運行更多的試驗和迭代,我們可以期待性能的進一步提升。
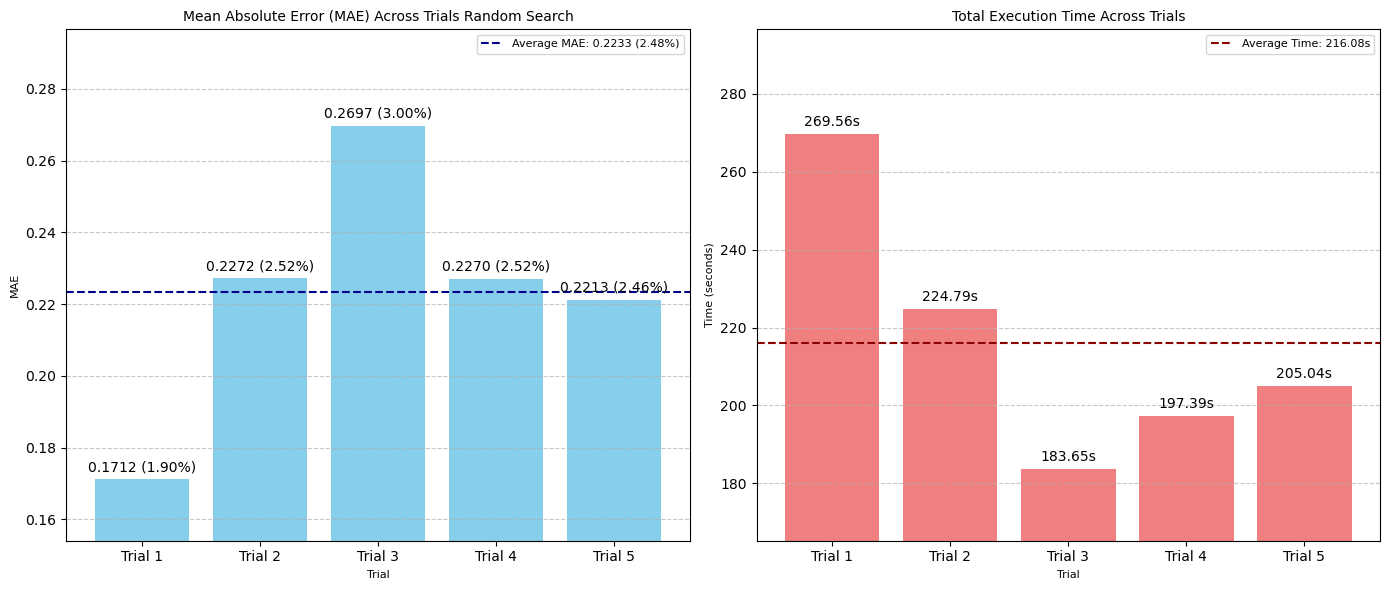
圖:五次隨機搜索試驗中 MAE(左)和搜索時間(秒)(右)的比較
- 最佳 MAE:0.1712 像素(1.90% 誤差范圍)
- 平均 MAE:0.2233 像素(2.48% 誤差范圍)/ 試驗
- 平均執行時間:216.08 秒 / 試驗
- 評估總數:50 次 / 試驗
- 最佳超參數集:
learning_rate: 0.010918659801547131, epochs: 200, num_conv_layers: 2, dense_units: 96, dropout: 0.0, filters_0: 32, batch_norm_0: True, filters_1: 32, batch_norm_1: False
注意:最優的 learning_rate 是 0.010918,證明了其評估連續值的能力。
6. 貝葉斯優化
與網格搜索或隨機搜索不同,貝葉斯優化利用一種智能、樣本高效的搜索方法,首先通過構建一個概率的代理模型(通常是高斯過程)。
高斯過程近似搜索空間中的目標函數,并估計每個搜索點的高斯(正態)分布。
通過這個過程,貝葉斯優化可以查看具有置信區間的潛在搜索點的預期收益。
例如:
- 搜索點(超參數組合)A:預期收益 μ=150\mu = 150μ=150,不確定性(風險)sigma2=100sigma^2 = 100sigma2=100 → 高風險,高收益 → 探索
- 搜索點(超參數組合)B:預期收益 μ=20\mu = 20μ=20,不確定性(風險)$\sigma^2 = 20$ → 低不確定性,低收益 → 有前景的點
為了決定下一步要評估哪個點,貝葉斯優化使用采集函數來量化這些預期值和不確定性,根據所選策略識別最有前景或最具探索性的點。
貝葉斯優化在給定迭代次數內持續這個搜索過程:
- 初始化:對目標函數進行少量初始隨機評估。
- 訓練代理模型:使用搜索空間中的樣本訓練代理模型。代理模型生成整個搜索空間上的均值 μ(x)\mu(x)μ(x)和方差 σ2(x)\sigma^2(x)σ2(x)。
- 計算采集函數:使用均值和方差計算搜索空間上的采集函數。
- 尋找下一個評估點:選擇使采集函數最大化(或最小化)的點 xnextx_{\text{next}}xnext?。
- 評估目標函數:在 xnextx_{\text{next}}xnext? 處運行實際目標函數以獲得真實的函數值 ynexty_{\text{next}}ynext?。
- 更新數據并重復:將 (xnextx_{\text{next}}xnext?, ynexty_{\text{next}}ynext?) 添加到觀測數據集中,并返回步驟 2。
當我們調優像 CNN 這樣的復雜模型時,步驟 5 的計算成本很高。
貝葉斯優化試圖通過有效地搜索下一個要測試的最佳組合來最小化步驟 5 的運行次數。
最佳使用場景:
- 昂貴的目標函數:非常適合單個訓練運行和評估非常耗時的模型(例如,深度神經網絡)。
- 有限的評估預算:需要以最少的試驗次數找到最優超參數。
- 復雜且非凸的搜索空間:當超參數和模型性能之間的關系是非線性且難以手動導航,存在許多局部最優解,搜索算法可能陷入其中。
局限性:
- 實現起來可能比網格搜索或隨機搜索更復雜。
- 由于需要維護和更新代理模型,每次迭代的計算開銷更高。
- 在非常高維的超參數空間中可能表現不佳。
6.1 選擇代理模型
了解貝葉斯優化如何工作后,我將在本節中探索其代理模型。
除了高斯過程(GPs),貝葉斯優化還可以利用各種代理模型。主要例子包括:
- 隨機森林 (RF):決策樹的集成;適用于混合數據類型,可以從樹的方差中估計不確定性。
- 樹結構 Parzen 估計器 (TPE):對好的和壞的超參數配置的密度進行建模以提出新的點;擅長處理分類和條件空間。
- 貝葉斯神經網絡 (BNN):由于概率權重,神經網絡輸出預測的分布,本質上提供了不確定性。
- 深度核學習 (DKL):結合神經網絡進行特征學習和高斯過程進行魯棒建模和不確定性量化。
- 模型集成:使用多個更簡單的模型來增強魯棒性并改進不確定性估計。
代理模型的選擇取決于優化問題和搜索空間的特性。例如,
- 高維搜索空間:最佳:TPE、BNN、DKL,最差:RF
- 混合超參數:最佳:TPE、RF,最差:傳統高斯過程
- 有限計算預算:最佳:TPE、RF,最差:BNN、DKL
- 精度要求高的項目(例如,藥物發現項目,其中精確預測是必需的):最佳:傳統高斯過程、DKL,最差:TPE、RF
我將在本文中重點介紹高斯過程,因為它具有一般優勢:
- 可靠的不確定性量化
- 在貝葉斯優化通常遇到的低數據量情況下表現出色。
6.2 高斯過程的數學形式
正如我們之前討論的,高斯過程是一個概率模型,它生成一個關于所有可能擬合給定數據的函數的分布。
想象我們有三組數據 (x, y):
- (1, 2)
- (2, 4)
- (3, 3)
以及預測點:x = 2.5
例如,線性回歸試圖使用這三個數據點找到一個近似函數,計算當 x=2.5x = 2.5x=2.5 時的預測值 y^\hat{y}y^?,并根據它們的近似函數(比如):y^=0.5x+2\hat{y} = 0.5x + 2y^?=0.5x+2 輸出一個單一值:y^=3.75\hat{y} = 3.75y^?=3.75。
另一方面,高斯過程在預測點生成一個高斯分布而不是單一值。
例如,高斯過程會輸出在 x=2.5x = 2.5x=2.5 處的預測值 ~N(μ,σ2)\sim N(\mu, \sigma^2)~N(μ,σ2),其中均值 μ≈3.28\mu \approx 3.28μ≈3.28,方差 σ2≈0.15\sigma^2 \approx 0.15σ2≈0.15。
在數學上,這個輸出被概括為后驗概率,如下所示:
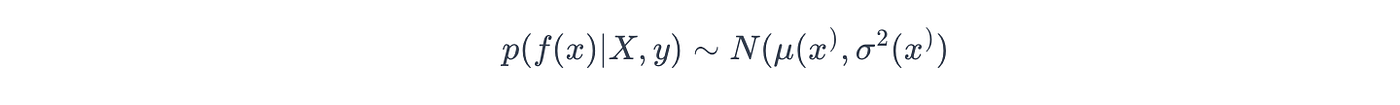
其中 μ(x?)\mu(x^*)μ(x?) 和 σ2(x?)\sigma^2(x^*)σ2(x?) 表示給定數據集 (X, y) 時預測點 (x?x^*x?) 處的均值/方差函數。
高斯過程的其他關鍵特征包括:
- 概率模型:在預測點生成一個關于所有可能函數的高斯分布,而不是單個值或標簽。
- 不確定性量化:使用估計高斯分布的方差量化預測中的不確定性(因此,我們可以看到其預測的置信水平)。
- 多元正態分布:假設任何有限的隨機變量集合都具有多元高斯分布,其均值和協方差由均值函數和核(協方差)函數定義。
- 非參數:不假設具有預定參數數量的固定函數形式。
- 靈活性:通過選擇不同的核函數可以建模各種函數形狀。
- 貝葉斯框架:遵循自然的貝葉斯框架,從先驗分布開始,并在觀察數據后將先驗更新為后驗分布。
計算后驗概率
利用其遵循貝葉斯框架的特性,高斯過程首先定義其對潛在真實函數 f(x)f(x)f(x) 的先驗信念,如下所示:
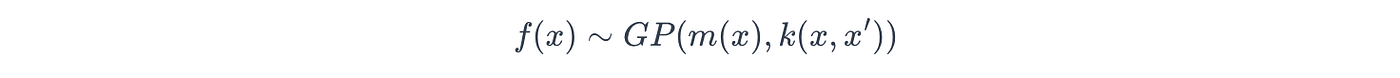
其中:
- m(x)m(x)m(x):先驗均值函數
- k(x,x′)k(x, x')k(x,x′):先驗核(協方差)函數。
然后,高斯過程使用此先驗計算后驗概率。
由于高斯過程假設隨機變量服從多元高斯分布,目標 yyy 和真實值 f(x)f(x)f(x) 的聯合先驗分布(同時觀察到 yyy 和 f(x)f(x)f(x) 的可能性)定義如下:
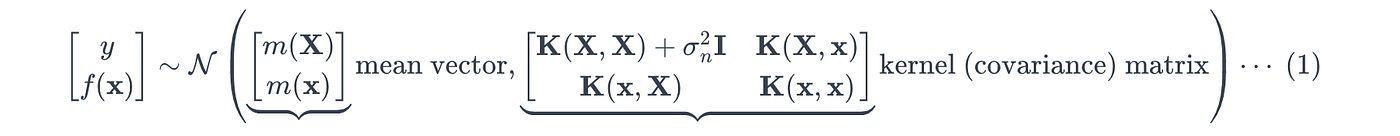
其中:

*對于高斯噪聲,高斯過程假設目標變量 yyy 被獨立高斯噪聲 ?\epsilon? 污染,使得:
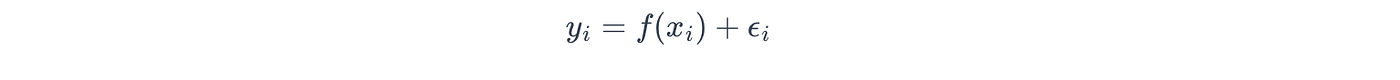
其中噪聲是從具有噪聲方差 σn\sigma_nσn? 的高斯分布中提取的:
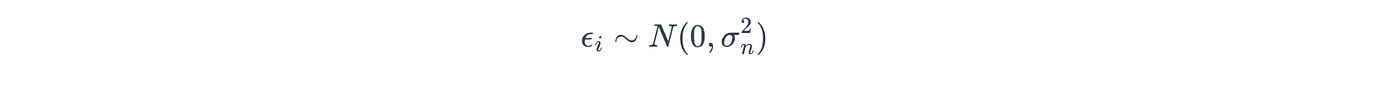
利用多元高斯分布的條件分布性質在公式 (1) 上,高斯過程計算預測點 x?x^*x? 處的后驗概率,其均值 μ(x?)\mu(x^*)μ(x?) 和方差 σ2(x?)\sigma^2(x^*)σ2(x?) 定義如下:

這些方程展示了高斯過程如何根據觀測數據調整先驗。
特別是,K(X,X)+σn2IK(X, X) + \sigma_n^2 IK(X,X)+σn2?I 的逆表示觀測數據的影響,權衡每個觀測對預測的貢獻以及方差減少的程度。
在這里,不同的核函數 K 編碼了關于底層函數的平滑度、周期性或其他屬性的不同假設。這使得高斯過程能夠靈活地學習各種函數。
6.3 在搜索空間中尋找下一個評估點
在高斯過程估計后驗分布后,貝葉斯優化利用采集函數計算每個搜索點的效用分數,使用高斯過程估計的均值和方差。
貝葉斯優化中常用的采集函數之一是預期改進 (EI):
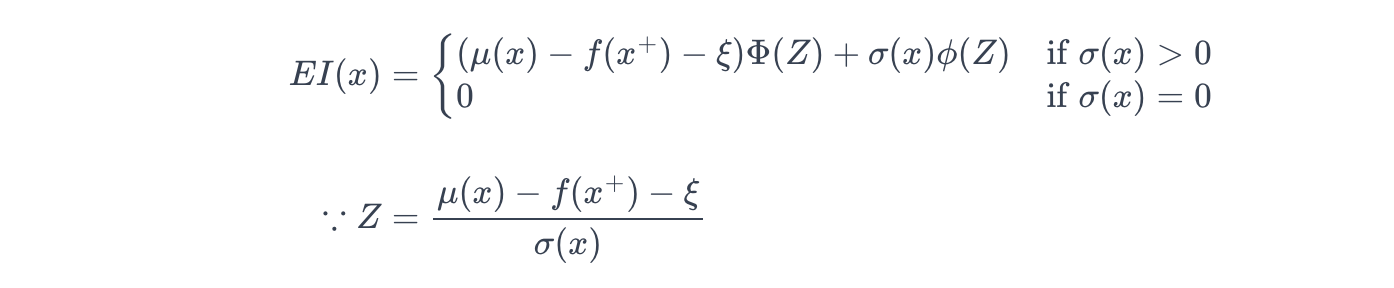
其中:
- μ(x)\mu(x)μ(x):高斯過程給出的點 x 處的預測均值
- f(x+)f(x^+)f(x+):當前最佳值
- ξ≥0\xi \geq 0ξ≥0:探索-利用權衡參數。較大的 ξ\xiξ 鼓勵更多的探索,而 ξ=0\xi = 0ξ=0 則純粹關注最大化預期收益。
- μ(x)?f(x+)\mu(x) - f(x^+)μ(x)?f(x+):相對于當前最佳的預測改進。
- μ(x)?f(x+)?ξ\mu(x) - f(x^+) - \xiμ(x)?f(x+)?ξ:在考慮點 x 時潛在的收益。
- σ(x)\sigma(x)σ(x):高斯過程給出的點 x 處的預測標準差。
- ZZZ:一個標準化分數(z-score),通過不確定性對潛在收益進行歸一化。
- Φ(Z)\Phi(Z)Φ(Z) / ?(Z)\phi(Z)?(Z):在 Z 處評估的標準正態分布的累積分布函數 (CDF) / 概率密度函數 (PDF)。
當點 x 處沒有不確定性時(因此 σ(x)=0\sigma(x) = 0σ(x)=0),EI 值為零,因為沒有進一步預期收益的潛力。
相反,當存在不確定性時 (σ(x)>0\sigma(x) > 0σ(x)>0),EI 根據相對于當前最佳的預測改進計算點 x 處的潛在收益,同時使用 ξ\xiξ 平衡探索和利用。
因此,更高的 EI(x) 值意味著當系統接下來探索 x 時,x 具有更大的預期收益。
貝葉斯優化會選擇這樣的點進行下一步探索。
6.4 搜索空間
與隨機搜索類似,貝葉斯優化受益于廣闊的搜索空間,這主要是因為廣闊的搜索空間顯著降低了錯過真正全局最優解的風險。
其由高斯過程引導的探索-利用平衡使其能夠有效地識別有前景的區域,即使在廣闊的超參數空間中也是如此。
因此,我為貝葉斯優化使用了與隨機搜索相同的搜索空間。
6.5 模擬
我利用 Keras-Tuner 庫中的 BayesianOptimization 類,進行了五次試驗,每次包含 50 個子集,以解決其隨機性。我取了平均和最佳 MAE。
import time
import keras_tuner as ktmax_trials = 50
tuner = kt.BayesianOptimization( hypermodel=build_cnn_model_keras, objective=kt.Objective("val_mae", direction="min"), max_trials=max_trials, executions_per_trial=1, overwrite=True, directory="my_tuning_dir", project_name="cnn_bayesian_tuning"
)start_tuning_time = time.time()
tuner.search(X_train, y_train, epochs=50, validation_data=(X_val, y_val))
end_tuning_time = time.time()best_model = tuner.get_best_models(num_models=1)[0]
best_trial = tuner.oracle.get_best_trials(num_trials=1)[0]
best_hparams = best_trial.hyperparameters
best_mae = best_trial.metrics.get_last_value('val_mae')
total_time = end_tuning_time - start_tuning_time
eval_count = max_trials
return best_mae, eval_count, total_time, best_hparams, best_model
6.6 結果
貝葉斯優化略低于隨機搜索的表現,完成一次包含 50 次測試的試驗需要 661 秒(約 11 分鐘)。
然而,這種方法在手動和網格搜索方法之間提供了平衡。增加試驗次數和每次試驗的測試數量可以進一步提高性能。
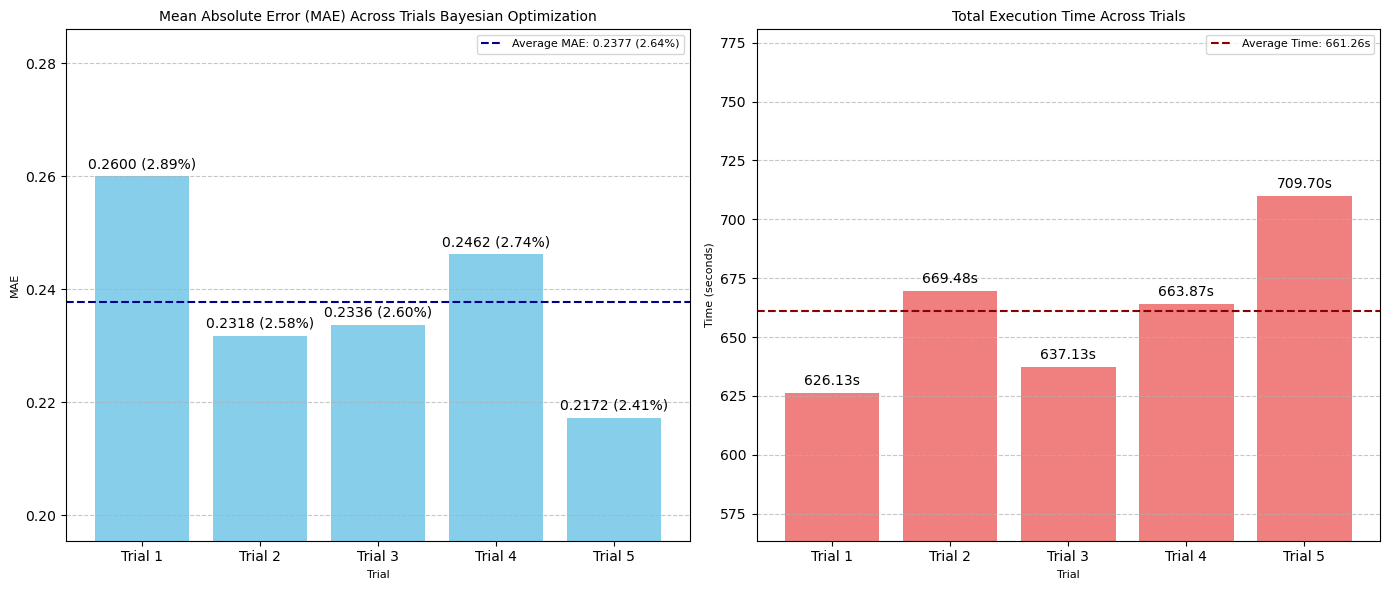
圖:五次貝葉斯優化試驗中 MAE(左)和搜索時間(秒)(右)的比較
- 最佳 MAE:0.2172 像素(2.41% 誤差范圍)
- 平均 MAE:0.2377 像素(2.64% 誤差范圍)/ 試驗
- 平均執行時間:661.26 秒 / 試驗
- 評估總數:50 次 / 試驗
- 最佳超參數集:
num_conv_layers: 1, dropout: 0, dense_units: 32, learning_rate: 0.0001, epochs: 1000, filters_0: 16, batch_norm_0: False
7. 元啟發式算法
元啟發式算法是用于解決傳統方法難以或不可能解決的復雜問題的優化技術,尤其是在處理極其龐大的搜索空間時。
它們不保證找到全局最優解,但旨在在合理的時間內找到一個“足夠好”(次優)的解。
其主要特點包括:
- 受自然/啟發式啟發:受自然現象、生物過程或人類行為啟發。
- 隨機性:在其搜索過程中包含隨機性,探索解決方案空間的不同部分,避免陷入局部最優(因此,擅長處理非常規搜索空間)。
- 探索與利用的平衡:像貝葉斯優化一樣,平衡探索和利用。
- 問題獨立性:通過最小的修改即可適用于各種優化問題。
- 迭代過程:通過多代(迭代)細化一組候選解。
- 適應度函數:使用適應度函數(目標函數)評估每個候選解(在我們的案例中是超參數集)的質量。
最佳使用場景:
- 高度復雜、非凸和不連續的搜索空間:當傳統的基于梯度的方法不適用或無法有效找到全局最優解時。
- 全局優化至關重要:需要探索各種解決方案并避免陷入局部最優。
局限性:
- 計算密集。
- 性能可能取決于其自身模型參數的調優。
7.1 元啟發式算法如何工作
以下是簡化步驟:
- 初始化:在問題搜索空間內隨機生成一組初始候選解(稱為種群)。
- 評估:使用目標函數評估每個候選解的適應度。
- 更新/改進:通過應用其底層隱喻啟發的特定規則,生成具有更好適應度值的新、可能更好的種群。該過程包括:
- 變異:隨機變異現有解決方案以引入多樣性。
- 交叉:組合好的解決方案的部分以創建新的解決方案。
- 移動:粒子或代理根據自己的最佳經驗在搜索空間中移動。
- 接受準則:決定是否接受新解決方案(尤其是在早期階段,以促進探索)。
4. 選擇:選擇最佳種群,同時淘汰適應度較低的解決方案。
5. 終止:重復步驟 2 到 4 直到收斂。
7.2 元啟發式算法的類型
元啟發式算法可以根據其靈感大致分類:
進化算法 (EAs):受生物進化和自然選擇啟發。
- 遺傳算法:模仿變異、交叉和選擇等過程來進化解決方案。
- 差分進化:使用向量差來創建新的候選解。
- 進化策略:側重于變異參數的自適應。
群智能 (SI) 算法:受分散、自組織系統的集體行為啟發。
- 粒子群優化:模擬鳥群或魚群的社會行為。
- 蟻群優化:基于螞蟻尋找食物最短路徑的覓食行為。
- 人工蜂群:模擬蜜蜂群的智能覓食行為。
基于物理的算法:受物理現象啟發。
- 模擬退火:類似于冶金中的退火過程,材料被加熱然后緩慢冷卻以減少缺陷。
- 引力搜索算法:基于萬有引力定律和質量相互作用。
基于人類的算法:受人類行為或社會互動啟發。
- 禁忌搜索:使用“禁忌列表”以避免重復訪問以前探索過的解決方案。
- 教與學優化:模仿課堂中的教與學過程。
7.3 搜索空間
與貝葉斯優化和隨機搜索類似,為元啟發式算法設置廣闊的搜索空間是有益的,因為它可以定義初始種群和后續世代的更大多樣性。
這將使它們能夠更廣泛地探索并逃離局部最優。
因此,我使用了與隨機搜索和貝葉斯優化相同的廣闊搜索空間。
7.4 模擬
在這里,我將以一種常見的元啟發式算法——遺傳算法 (GA) 為例。
遺傳算法模仿自然選擇來進化物種。
在超參數調優中,“物種”是超參數組合的種群,它們通過偏愛“存活率更高”的個體(在我們的案例中表示更好的 MAE)來隨代進化。
讓我們一步一步地探索它的迭代方法。
7.4.1 步驟 1. 初始化:創建種群
我設置了一個包含十個個體的初始種群:
import randomdef create_individual(): hparams = dict()hparams['num_conv_layers'] = random.choice(hparams_options['num_conv_layers']) for i in range(hparams['num_conv_layers']): hparams[f'filters_{i}'] = random.choice(hparams_options[f'filters_{i}']) hparams[f'batch_norm_{i}'] = random.choice(hparams_options[f'batch_norm_{i}']) hparams['dense_units'] = random.choice(hparams_options['dense_units']) hparams['epochs'] = random.choice(hparams_options['epochs'])hparams['learning_rate'] = random.uniform(hparams_options['learning_rate'][0], hparams_options['learning_rate'][-1]) hparams['dropout'] = random.uniform(hparams_options['dropout'][0], hparams_options['dropout'][-1])return hparamspopulation_size = 10
population = [create_individual() for _ in range(population_size)]
7.4.2 步驟 2. 評估:計算適應度分數
接下來,計算了種群中所有個體的適應度分數,并選擇了表現最佳的個體:
eval_count = 0
total_time = 0.0best_mae = float('inf')
best_hparams = None
best_model = None
n_generations = 10for _ in range(n_generations): fitnesses = list()for indiv in population: eval_count_returned, total_time_returned, mae, model = evaluate_model(hparams=indiv) fitnesses.append(accuracy) eval_count += eval_count_returned total_time += total_time_returnedcurrent_best_idx = np.argmin(fitnesses) current_best_mae = fitnesses[current_best_idx] current_best_params = population[current_best_idx]if current_best_mae < best_mae: best_mae = current_best_mae best_params = current_best_params best_model = model
7.4.3 步驟 3: 迭代
在迭代循環中,遺傳算法通過選擇適應度分數最高的 10%(或您選擇的任何百分比)的高表現者(elites)來構建新種群。
我選擇了 MAE 最低的最佳個體:
import numpy as npnew_population = []num_elites = max(1, int(0.1 * population_size))
elites = sorted(zip(population, fitnesses), key=lambda x: x[1], reverse=False)[:num_elites]
new_population.extend([e[0] for e in elites])
然后,通過生成九個變異的后代來更新十個個體的種群:
import randomnum_parentes_to_select = population_size - num_elites
total_fitness = sum(fitnesses)
probabilities = [f / total_fitness for f in fitnesses]
indices = np.random.choice( len(population), size=num_parentes_to_select, p=probabilities, replace=True
)
parents = [population[i] for i in indices]def crossover(parent1, parent2, crossover_rate): offspring1 = parent1.copy() offspring2 = parent2.copy() if random.random() < crossover_rate: offspring1['num_conv_layers'] = random.choice([parent1['num_conv_layers'], parent2['num_conv_layers']]) offspring2['num_conv_layers'] = random.choice([parent1['num_conv_layers'], parent2['num_conv_layers']]) for param in ['dense_units', 'dropout', 'learning_rate', 'epochs']: if random.random() < crossover_rate: offspring1[param], offspring2[param] = parent2[param], parent1[param]for offspring in [offspring1, offspring2]: for i in range(offspring['num_conv_layers']): if f'filters_{i}' not in offspring: offspring[f'filters_{i}'] = random.choice(hparams_options['filters_0']) if f'batch_norm_{i}' not in offspring: offspring[f'batch_norm_{i}'] = random.choice(hparams_options['batch_norm_0']) return offspring1, offspring2def mutate(individual): mutated_individual = individual.copy()if random.random() < mutation_rate: mutated_individual['num_conv_layers'] = random.choice(hparams_options['num_conv_layers']) for i in range(max(hparams_options['num_conv_layers'])): if i < mutated_individual['num_conv_layers']: if f'filters_{i}' not in mutated_individual or random.random() < mutation_rate: mutated_individual[f'filters_{i}'] = random.choice(hparams_options['filters_0']) if f'batch_norm_{i}' not in mutated_individual or random.random() < mutation_rate: mutated_individual[f'batch_norm_{i}'] = random.choice(hparams_options['batch_norm_0']) else: mutated_individual.pop(f'filters_{i}', None) mutated_individual.pop(f'batch_norm_{i}', None) if random.random() < mutation_rate: mutated_individual['dense_units'] = random.choice(hparams_options['dense_units']) if random.random() < mutation_rate: mutated_individual['dropout'] = random.uniform(hparams_options['dropout'][0], hparams_options['dropout'][-1]) if random.random() < mutation_rate: mutated_individual['learning_rate'] = random.uniform(hparams_options['learning_rate'][0], hparams_options['learning_rate'][-1]) if random.random() < mutation_rate: mutated_individual['epochs'] = random.choice(hparams_options['epochs']) return mutated_individualcrossover_rate = 0.8
mutation_rate = 0.1
for i in range(0, len(parents), 2): if len(new_population) >= population_size: breakparent1 = parents[i] parent2 = parents[i+1] offspring1, offspring2 = crossover(parent1, parent2, crossover_rate)new_population.append(mutate(offspring1)) if len(new_population) < population_size: new_population.append(mutate(offspring2))while len(new_population) < population_size: new_population.append(mutate(random.choice(elites)[0]))population = new_population
7.4.4 步驟 4 & 5: 選擇最佳參數
我重復這個過程五代,每代創建十個組合(個體):
n_generations = 5for _ in range(n_generations): fitnesses = list() for indiv in population: eval_count_returned, total_time_returned, mae, model = evaluate_model(hparams=indiv) fitnesses.append(accuracy) eval_count += eval_count_returned total_time += total_time_returnedcurrent_best_idx = np.argmin(fitnesses) current_best_mae = fitnesses[current_best_idx] current_best_params = population[current_best_idx]if current_best_mae < best_mae: best_mae = current_best_mae best_params = current_best_params best_model = modelnew_population = [] num_elites = max(1, int(0.1 * population_size)) elites = sorted(zip(population, fitnesses), key=lambda x: x[1], reverse=False)[:num_elites] new_population.extend([e[0] for e in elites]) num_offspring = population_size - num_elites parents = select_parents(population, fitnesses, num_offspring)for i in range(0, len(parents), 2): if len(new_population) >= population_size: break parent1 = parents[i] parent2 = parents[i+1] offspring1, offspring2 = crossover(parent1, parent2, crossover_rate) new_population.append(mutate(offspring1)) if len(new_population) < population_size: new_population.append(mutate(offspring2))while len(new_population) < population_size: new_population.append(mutate(random.choice(elites)[0]))population = new_populationreturn best_mae, eval_count, total_time, best_hparams, best_model
7.5 結果
遺傳算法表現出廣泛的性能范圍,產生了 2.36% 的最佳誤差范圍,超過了網格搜索,并且以**最有效的時間成本(188 秒,約 3 分鐘)**完成了 50 次 CNN 測試。
然而,其最差誤差范圍(第二次試驗時為 3.67%)是所有方法和試驗中最高的。
這表明遺傳算法固有的隨機性,它比網格搜索等方法更動態、更不系統地探索搜索空間。
雖然這允許逃離局部最優,但它也可能導致不同運行或試驗的性能和收斂速度的可變性。
在我們的案例中,由于第二次試驗,遺傳算法的平均 MAE 在四種自動化方法中是最高的。
運行更多試驗并增加世代數可能會帶來更好的結果。
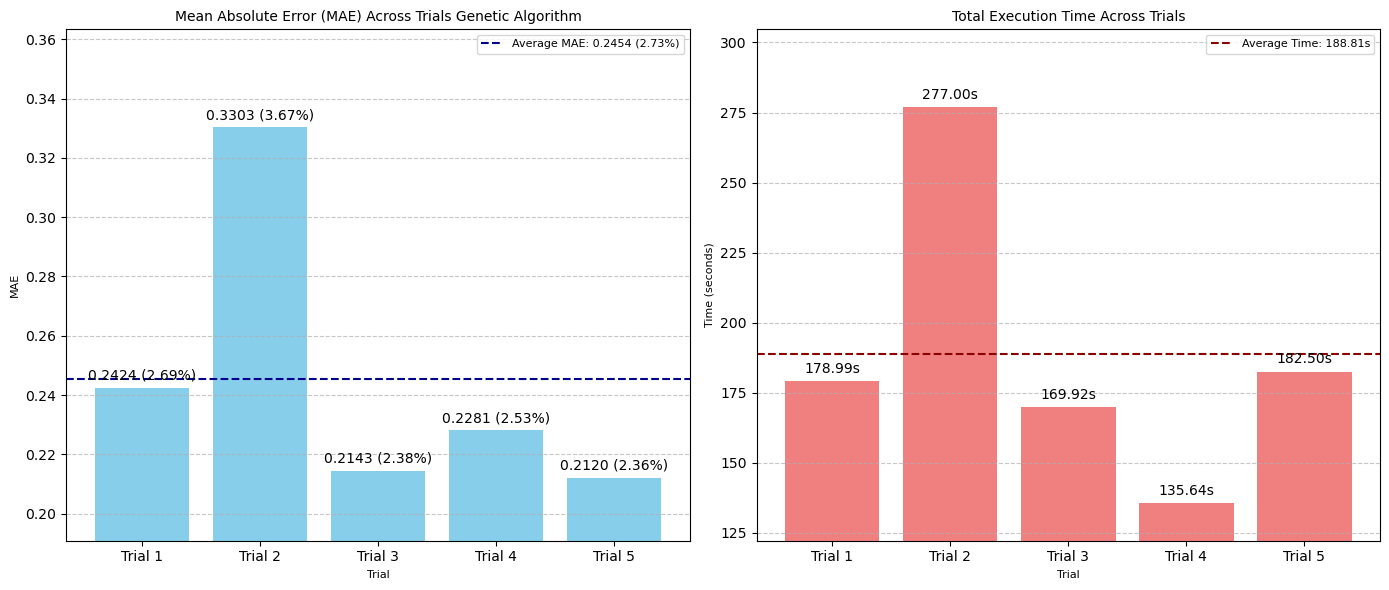
圖:五次遺傳算法試驗中 MAE(左)和搜索時間(秒)(右)的比較(
- 最佳 MAE:0.2120 像素(2.36% 誤差范圍)
- 平均 MAE:0.2454 像素(2.73% 誤差范圍)/ 試驗
- 平均執行時間:188.81 秒 / 試驗
- 評估總數:50 次 / 試驗
- 最佳超參數集:
num_conv_layers: 1, dropout: 0, dense_units: 32, learning_rate: 0.0001, epochs: 1000, filters_0: 16, batch_norm_0: False
8. 泛化能力和時間效率的最終評估
在評估這五種方法時,泛化性能(通過測試數據集上的 MAE 衡量)是最關鍵的指標,它表明模型在未見過數據上的表現能力。
然后,時間效率也是一個重要的考慮因素,尤其是在計算資源有限的情況下。
下表展示了所有五種方法的平均和最佳結果以及我實施的搜索策略摘要:

圖:超參數調優方法在 CNN 上的性能比較和搜索策略(泛化:測試數據集上的 MAE 分數,總時間:總搜索時間(秒),平均時間:每次評估的平均時間(秒)(總時間/評估次數))
8.1 泛化能力
在自動化方法中,隨機搜索和貝葉斯優化實現了最佳的泛化性能,誤差率約為 2.53%。
它們強大的泛化能力得到了進一步支持,即搜索期間的最佳 MAE 與其泛化 MAE 之間的差異極小。
相比之下,遺傳算法顯示出輕微的過擬合傾向,其搜索誤差率與泛化誤差率之間存在 0.35 個百分點的差距。
網格搜索雖然比手動搜索有所改進,但最終泛化能力最差,這表明擴大其搜索空間可以提高性能。
8.2 時間效率
在時間效率方面,遺傳算法被證明是最有效的自動化方法,每次評估的平均時間為 3.65 秒,50 次評估的總時間為 182.50 秒。
隨機搜索也非常高效,平均時間為 4.10 秒,總時間為 205.04 秒。
相比之下,貝葉斯優化盡管具有競爭性的泛化能力,但時間效率最低,每次評估的平均時間為 14.19 秒,總時間高達 709.70 秒。
這表明了貝葉斯優化的本質。它旨在樣本高效,需要更少的昂貴目標函數的實際評估,但引入了與構建和優化概率代理模型(高斯過程)相關的自身計算開銷。
當單個目標函數不那么昂貴時,這種開銷可能使總時間比隨機搜索等更簡單的方法更長。
總之,對于本次實驗,隨機搜索在泛化和時間效率方面都取得了最佳結果。
9. 針對表格數據上訓練的簡單模型
現在,在理解了每種方法在復雜模型上的表現后,本節將探討相同的五種方法在更簡單的模型上,即在包含 3,000 個數據點的表格數據集上訓練的核 SVM:
9.1 表格數據
我從一個包含 10 個特征的 3,000 個合成表格數據集創建了訓練、驗證和測試數據集:
import numpy as np
from sklearn.model_selection import train_test_splitn_samples = 10000
n_features = 10
test_size = 1000
random_state = 42
np.random.seed(random_state)X = np.zeros((n_samples, n_features))
X[:, 0] = np.random.uniform(-5, 5, n_samples)
X[:, 1] = np.random.normal(0, 3, n_samples)
X[:, 2] = np.random.uniform(-10, 10, n_samples)
if n_features > 3: X[:, 3] = np.random.normal(5, 2, n_samples)y = np.zeros(n_samples)
y += 2 * X[:, 0] + 5
y += 0.5 * (X[:, 1] ** 2) - 3 * X[:, 1]
y += 10 * np.sin(X[:, 2] / 2)
y += 0.7 * X[:, 0] * X[:, 3]
noise = np.random.normal(0, 2, n_samples) * (1 + 0.1 * np.abs(X[:, 0]))
y += noiseX_tv, X_test, y_tv, y_test = train_test_split(X, y, test_size=test_size, random_state=random_state)
X_train, X_val, y_train, y_val = train_test_split(X_tv, y_tv, test_size=test_size, random_state=random_state)from sklearn.preprocessing import StandardScalerscaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_val = scaler.transform(X_val)
X_test = scaler.transform(X_test)
print(X_train.shape, y_train.shape, X_val.shape, y_val.shape, X_test.shape, y_test.shape)
(8000, 10) (8000,) (1000, 10) (1000,) (1000, 10) (1000,)
目標變量的范圍:[-51.58330487465222, 125.96875771528616]
9.2 搜索空間
與 CNN 案例采取類似策略,我為隨機搜索、貝葉斯優化和遺傳算法定義了一個更廣闊的搜索空間,其中包含離散和連續選項:
hparams_options = { 'kernel': ['linear', 'poly', 'rbf', 'sigmoid'], 'gamma': ['auto', 'scale', 1, 0.1, 0.05, 0.01, 0.001], 'max_iter': [i for i in range(50, 3001)],'tol': [0.1, 0.0001], 'coef0': [0.1, 1.0], 'C': [0.1, 10], 'epsilon': [0.1, 0.0001],
}
對于網格搜索,將搜索空間縮小到只有離散選項:
hparams_options = { 'kernel': ['linear', 'poly', 'rbf', 'sigmoid'], 'gamma': ['auto', 'scale', 1, 0.1, 0.05, 0.01, 0.001], 'max_iter': [100, 300, 500] 'tol': [0.01, 0.001], 'C': [0.1, 1, 10], 'epsilon': [0.001, 0.0001],
}
注意:核 SVM 比 CNN 簡單得多,超參數組合數量有限。在廣闊的搜索空間中運行網格搜索可能是一個選擇。
9.3 評估模型
雖然是可選的,但建議對更簡單的 Scikit-learn 模型使用 K 折交叉驗證,以確保在未見過的數據上獲得穩定的性能。
我定義了 build_evaluate_model 函數來處理每個模型的構建、訓練和評估,循環五折:
import time
from sklearn.svm import SVR
from sklearn.model_selection import KFold
from sklearn.metrics import mean_absolute_errordef build_evaluate_model(hparams: dict, eval_count: int = 0, total_time: float = 0.0, n_splits: int = 5) -> tuple: kernel = hparams.get('kernel', 'rbf') degree = hparams.get('degree', 3) gamma = hparams.get('gamma', 'scale') coef0 = hparams.get('coef0', 0) tol = hparams.get('tol', 0.001) C = hparams.get('C', 1) epsilon = hparams.get('epsilon', 0.1) max_iter = hparams.get('max_iter', 100) start_time = time.time()maes = 0 kf = KFold(n_splits=n_splits, shuffle=True, random_state=42) for train_index, val_index in kf.split(X_train): X_train_fold, X_val_fold = X_train[train_index], X_train[val_index] y_train_fold, y_val_fold = y_train[train_index], y_train[val_index]model = SVR( kernel=kernel, degree=degree, gamma=gamma, coef0=coef0, tol=tol, C=C, epsilon=epsilon, max_iter=max_iter, verbose=False, ).fit(X_train_fold, y_train_fold)y_pred_val_kf = model.predict(X_val_fold) maes += mean_absolute_error(y_pred_val_kf, y_val_fold) eval_count += 1end_time = time.time() total_time += (end_time - start_time) ave_mae = maes / n_splits return eval_count, total_time, ave_mae
9.4 結果
結果表明,隨著采用更先進的優化策略,模型性能有所提高;貝葉斯優化在泛化誤差方面表現最佳(MAE: 2.4710,1.39% 誤差范圍)。
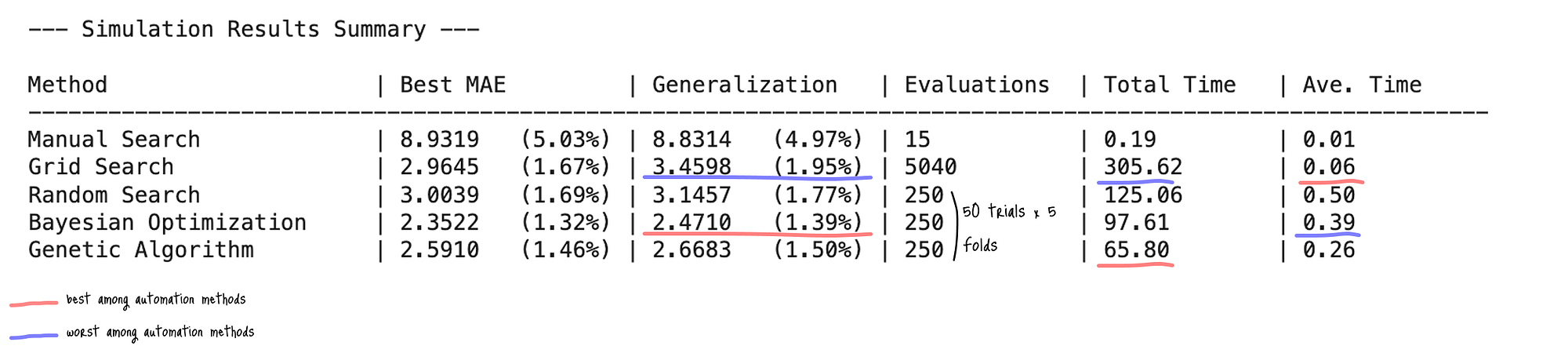
圖:超參數調優方法在 核 SVM 上的性能比較(泛化:測試數據集上的 MAE 分數,():誤差范圍,總時間:總搜索時間(秒),平均時間:每次評估的平均時間(秒)(總時間/評估次數))
現在,讓我們看看每種方法的性能。
9.4.1 手動搜索
手動搜索雖然計算量最小,但預測精度最差(MAE 為 8.8314 / 4.97% 誤差范圍),突出了其有效超參數調優的局限性。
最佳超參數集:
- kernel: ‘linear’
- gamma: 0.1
- tol: 0.01
- coef0: 1.0
- C: 1.0
- epsilon: 0.1
- max_iter: 50
9.4.2 網格搜索
網格搜索在 MAE (3.4598 / 1.95% 誤差范圍) 方面比手動調優有了顯著改進。
然而,其窮盡搜索導致了大量的評估次數(5,040 = 1,008 模式 x 5 折)和最長的實際執行時間(305.62 秒),這使得它對于更大的搜索空間來說效率低下。
最佳超參數集:
- kernel: “rbf”
- gamma: 1
- tol: 0.01
- coef0: 0
- C: 10
- epsilon: 0.0001
- max_iter: 500
9.4.3 隨機搜索
隨機搜索在其他隨機搜索方法中產生了中等結果,誤差范圍為 1.77%,經過 250 次評估(50 模式 x 5 折)。
與網格搜索相比,它在性能和執行時間方面都有所改進,使用的搜索次數更少(250 次 vs 5,040 次)。
最佳超參數集:
- kernel: “rbf”
- gamma: 1
- tol: 0.018670512147205817
- coef0: 0.24733542330773028
- C: 2.802020727787644
- epsilon: 0.0063082312071634505
- max_iter: 1,512
9.4.4 貝葉斯優化 (Scikit-Optimize)
貝葉斯優化在預測精度方面表現最佳,在訓練期間生成了最低的 MAE (2.3522) 和強大的泛化能力(MAE: 2.4710 / 1.39% 誤差范圍)。
它還在自動化方法中實現了最少的評估次數(250 次)。
然而,其概率建模方法使其成為最耗時的方法,導致每次評估的平均時間最高(0.39 秒)。
最佳超參數集:
- kernel: “rbf”
- gamma: 0.6283361736403552
- tol: 0.00061852605407886
- coef0: 0.15445767772707622
- C: 10.0
- epsilon: 0.0009534694901172961
- max_iter: 3,000
9.4.5 遺傳算法
遺傳算法在自動化方法中也表現出強大的性能(MAE 為 2.6683 / 1.50% 誤差范圍)。它還在65.8 秒內以最快的速度完成了相同的 250 次搜索。
增加世代數和種群規模可以進一步提高性能。
最佳超參數集:
- kernel: “rbf”
- gamma: 1
- tol: 0.05646743039011411
- coef0: 0.9662477750994501
- C: 10
- epsilon: 0.05000297689759651
- max_iter: 1,718
總而言之,當考慮計算時間與預測結果之間的權衡時,遺傳算法脫穎而出,提供了最佳平衡,以合理的計算成本提供了強大的性能。
貝葉斯優化雖然實現了最低的 MAE,但每次評估的計算開銷更高,這使得當我們將最佳峰值性能置于開銷之上時,它是一個不錯的選擇。
正如我們在 CNN 案例中看到的那樣,這種權衡對復雜模型提出了挑戰。
但對于像核 SVM 這樣計算效率高的表格數據集模型,貝葉斯優化可能是一個絕對的選擇,因為每次測試的時間明顯更快(0.39 秒)與 CNN(14.2 秒)相比。
10. 結論
在我們的實驗中,我們觀察到超參數調優方法的效果各不相同。
對于像 SVM 這樣的復雜和簡單模型,我們的發現表明,像遺傳算法這樣的高級隨機方法能產生最佳性能,平衡了最優結果和計算成本。
總而言之:
- 從快速手動搜索開始。
- 為了找到全局最優解,尤其是在小搜索空間中,嘗試網格搜索。
- 當次優解足夠好或唯一選擇時,嘗試隨機方法:
- 對于昂貴的目標函數,貝葉斯優化是一種高效的選擇,它平衡了計算成本和模型的泛化性能。
- 對于中等目標函數,隨機搜索由于其簡單性比貝葉斯優化更高效。
- 對于非凸、復雜的搜索空間,遺傳算法可以有效降低陷入局部最優的風險。
如果計算資源允許,我們的實驗建議:
- 對隨機方法進行多次試驗以標準化結果,
- 隨后,在具有競爭力的組合中選擇最常見的超參數值作為最終模型可能是一個可行的策略,并且
- 采用混合方法,首先使用隨機方法縮小搜索空間,然后應用網格搜索尋找全局最優解。
最終的選擇取決于模型復雜度、所需的預測能力以及每個項目中的實際計算限制。







)
)





,文件名由連續的數字編號+連續的字母編號組成,并分離出文件名數字部分和英文部分)




