目標:
1.理解后端的概念;
2.理解以EKF為代表的濾波器后端的工作原理;
3.理解非線性優化的后端,明白稀疏性是如何利用的;4.使用g2o和Ceres實際操作后端優化。
9.1 概述
9.1.1 狀態估計的概率解釋
1.后端優化引出
? ? ? ?前段視覺里程計僅能給出一個短時間內的軌跡和地圖,會造成誤差累積;
? ? ? ?后端優化(批量、漸進)解決長時間最優軌跡和地圖,“批量的”不僅使用過去的信息更新自己的狀態,也會用未來的信息來更新;“漸進的”指當前的狀態只由過去的時刻決定,甚至只由前一個時刻決定。
2.運動和觀測方程
SLAM過程可以由運動方程和觀測方程來描述。假設在t=0到t=N到的時間內,有位姿
到
,并且有路標
。運動和觀測方程為
(1)觀測方程中,只有當
看到了
時,才會產生觀測數據。事實上,在一個位置通常只能看到一小部分路標。而且,由于視覺SLAM特征點數量眾多、所以實際中觀測方程的數量會遠遠大于運動方程。
(2)可能沒有測量運動的裝置,也可能沒有運動方程。在這個情況下,有若干種處理方式:認為確實沒有運動方程,或假設相機不動,或假設相機勻速運動。這幾種方式都是可行的。在沒有運動方程的情況下,整個優化問題就只由許多個觀測方程組成。這就非常類似于SfM問題,相當于通過一組圖像來恢復運動和結構。不同的是,SLAM中的圖像有時間上的先后順序,而SfM中允許使用完全無關的圖像。
3.問題轉化
? ? ? ?每個方程都受噪聲影響,所以要把這里的位姿和路標看成服從某種概率分布的隨機變量,而不是單獨的一個數。
? ? ? ?因此,我們關心的問題就變成:當我們擁有某些運動數據和觀測數據時,如何確定狀態量的分布?進而,如果得到了新時刻的數據,它們的分布又將發生怎樣的變化?
? ? ? ?在比較常見且合理的情況下,假設狀態量和噪聲項服從高斯分布——這意味著在程序中只需要存儲它們的均值和協方差矩陣即可。均值可看作對變量最優值的估計,而協方差矩陣則度量了它的不確定性。
? ? ? ? 那么,問題就轉變為:當存在一些運動數據和觀測數據時,我們如何估計狀態量的高斯分布?
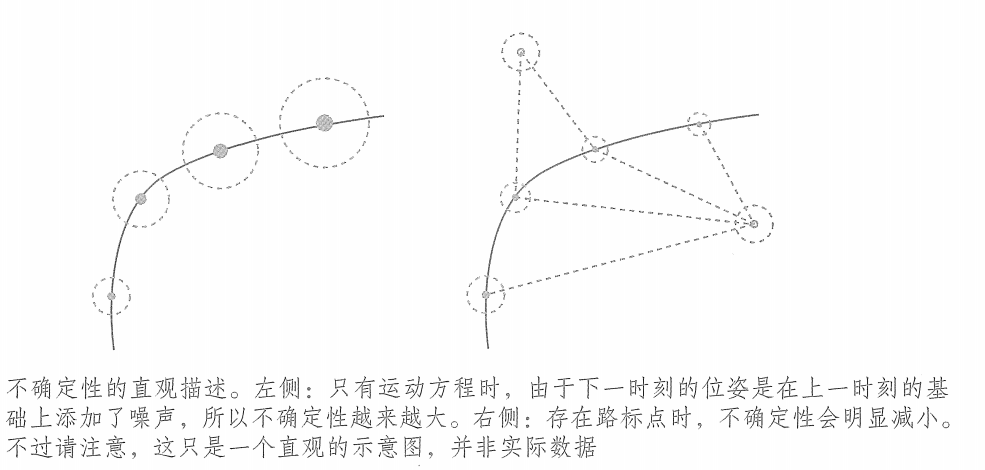
? ? ? ?只有運動方程時,相當于我們蒙著眼睛在一個未知的地方走路。盡管我們知道自己每一步走了多遠,但是隨著時間流逝,我們越來越不確定自己的位置——內心也就越不安。這說明當輸人數據受噪聲影響時,誤差是逐漸累積的,我們對位置方差的估計將越來越大。但若能不斷地觀測到外部場景,就會使得位置估計的不確定性變小。? ? ? ?如果用橢圓或橢球直觀地表達協方差陣,那么這個過程有點像是在手機地圖軟件中走路的感覺。
? ? ? ?以下圖為例,當沒有觀測數據時,這個圓會隨著運動越來越大;而如果有正確的觀測數據,圓就會縮小至一定的大小,保持穩定。
4.運算推導
? ? ? ?在第6講中,介紹了最大似然估計,提到批量狀態估計問題可以轉化為最大似然估計問題,并使用最小二乘法進行求解。如何將該結論應用于漸進式問題?在視覺SLAM 里,最小二乘法又有何特殊的結構?
(1)方程轉換
? ? ? ?首先,由于位姿和路標點都是待估計的變量,令
為k時刻的所有未知量。它包含了當前時刻的相機位姿與m個路標點。在這種記號的意義下寫成
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
? ? ? ?同時,把k時刻的所有觀測記作。這里不會出現y,但我們心里要明白這時心中已經包含了之前的y
?? ? ? ? ? ??
(2)通過過去的狀態估計當前狀態? ? ? ?現在考慮第k時刻的情況。我們希望用過去0到k中的數據來估計現在的狀態分布
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
下標0:k表示從0時刻到k時刻的所有數據。表示所有在時刻的觀測數據,它可能不止一個。
? ? ? ?同時,
實際上和這些量都有關,但是此式沒有顯式地將它們寫出來。
? ? ? ?下面看如何對狀態進行估計。按照貝葉斯法則,把
與
交換位置,有
? ? ? ?第一項稱為似然,第二項稱為先驗。似然由觀測方程給定,而先驗部分,我們要明白當前狀態是基于過去所有的狀態估計得來的。至少,它會受影響,于是以
時刻為條件概率展開
? ? ? ?如果考慮更久之前的狀態,也可以繼續對此式進行展開。(二階先驗、三階先驗..)? ? ? ?但現在我們只關心k時刻和k-1時刻的情況。至此,我們給出了貝葉斯估計,因為上式還沒有具體的概率分布形式,所以沒法實際操作它。對這一步的后續處理,方法上產生了一些分歧。
(3)卡爾曼濾波器與擴展卡爾曼濾波器
? ? ? ? 一種方法是假設馬爾可夫性,簡單的一階馬氏性認為,k時刻狀態只與k-1時刻狀態有關,而與再之前的無關。如果做出這樣的假設,我們就會得到以擴展卡爾曼濾波(EKF)為代表的濾波器方法。在濾波方法中,我們會從某時刻的狀態估計,推導到下一個時刻。
? ? ? ? 另一種方法是依然考慮k時刻狀態與之前所有狀態的關系,此時將得到非線性優化為主體的優化框架。目前,視覺SLAM的主流為非線性優化方法。
9.1.2 線性系統和KF
根據馬爾科夫性,式子
簡化為
? ? ? ?
? ? ? ?考慮到k時刻的輸入量
與k-1時刻的狀態無關,所以我們把
拿掉。
? ? ? ?可以看到,這一項實際上是k-1時刻的狀態分布。
? ? ? ?于是,這一系列方程說明,我們實際在做的是“如何把k-1時刻的狀態分布推導至時刻”這樣一件事。
? ? ? ? 也就是說,在程序運行期間,我們只要維護一個狀態量,對它不斷地進行迭代和更新即可。如果假設狀態量服從高斯分布,那么我們只需考慮維護狀態量的均值和協方差即可。
? ? ? ? 假設小蘿卜上的定位系統一直在向外輸出兩個定位信息:一是自己的位姿,二是自己的不確定性。實際中往往也是如此。
1.線性高斯到卡爾曼濾波器
線性高斯系統是指運動方程和觀測方程可以由線性方程來描述
? ? ? ? ? ? ? ? ? ? ??
假設所有的狀態和噪聲均滿足高斯分布,記這里的噪聲服從零均值高斯分布
? ? ? ? ? ? ? ? ? ? ? ??
? ? ? ?利用馬爾可夫性,假設我們知道了k-1時刻的后驗(在k-1時刻看來)狀態估計
及其協方差
,現在要根據k時刻的輸入和觀測數據,確定
的后驗分布。為區分推導中的先驗和后驗,我們在記號上做一點區別:以上帽子
表示后驗,以下帽子
表示先驗分布。
(1)
求解
卡爾曼濾波器的第一步,通過運動方程確定
的先驗分布。這一步是線性的,而高斯分布的線性變換仍是高斯分布所以有
?這一步稱為預測(Predict)。它顯示了如何從上一個時刻的狀態,根據輸入信息(但是有噪聲R)推斷當前時刻的狀態分布。這個分布也就是先驗。記
? ? ? ? ? ?
k時刻似然表達式
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?? ? ? ?為了得到后驗概率,我們想要計算它們的乘積。然而,雖然我們知道最后會得到一個關于
的高斯分布,我們先把結果設為
,那么
? ? ? ? ? ? ??
既然我們已經知道等式兩側都是高斯分布,那就只需比較指數部分,無須理會高斯分布前面的因子部分。指數部分很像是一個二次型的配方,我們來推導一下。首先把指數部分展開,有
為了求左側的
和???????
,我們把兩邊展開,并比較???????
的二次和一次系數。對于二次系數,有
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??
定義中間變量
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
左右乘以???????
,有
? ? ? ? ??
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??
比較一次性系數,有
? ? ? ? ? ? ?
取系數并轉置得
? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
兩側乘以
并帶入得
? ?
2.小結
總而言之,上面的兩個步驟可以歸納為“預測”和“更新”(Update)兩個個步驟:
(1)預測
? ? ? ? ? ?
(2)計算卡爾曼增益
? ? ? ? ? ? ? ? ? ? ? ? ?
? ? ? ? ?更新后驗概率的分布
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
? ? ? ?至此,已經推導了經典的卡爾曼濾波器的整個過程。我們使用從概率角度出發的最大后驗概率估計的方式。
? ? ? ?在線性高斯系統中,卡爾曼濾波器構成了該系統中的最大后驗概率估計。而且,由于高斯分布經過線性變換后仍服從高斯分布,所以整個過程中我們沒有進行任何的近似。可以說,卡爾曼濾波器構成了線性系統的最優無偏估計。
9.1.3 非線性系統和EKF
? ? ? ?在理解了卡爾曼濾波之后,我們必須要澄清一點:SLAM中的運動方程和觀測方程通常是非線性函數,尤其是視覺SLAM中的相機模型,需要使用相機內參模型及李代數表示的位姿,更不可能是一個線性系統。
? ? ? ?一個高斯分布,經過非線性變換后,往往不再是高斯分布。所以在非線性系統中,我們必須取一定的近似,將一個非高斯分布近似成高斯分布。
1.擴展卡爾曼濾波器(非線性)
? ? ? ?把卡爾曼濾波器的結果拓展到非線性系統中,稱為擴展卡爾曼濾波器。通常的做法是,在某個點附近考慮運動方程及觀測方程的一階泰勒展開,只保留一階項,即線性的部分,然后按照線性系統進行推導。
? ? ? ?令k-1時刻的均值與協方差矩陣為
,
。在k時刻,我們把運動方程和觀測方程在
,
處進行線性化(相當于一階泰勒展開),有
這里的偏導數為
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??
同樣,對于觀測方程,亦有
? ? ? ? ? ? ? ? ? ?
記這里偏導數為
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
那么,在預測步驟中,根據運動方程有
這些推導和卡爾曼濾波是十分相似的。為方便表述,記這里的先驗和協方差的均值為? ? ? ? ? ??
? ? ? ? ? ??然后,考慮在觀測中我們有
? ? ? ? ? ? ??
? ? ? ? 最后,根據最開始的貝葉斯展開式,可以推導出
的后驗概率形式。我們略去中間的推導過程,只介紹其結果。讀者可以仿照卡爾曼濾波器的方式,推導EKF的預測與更新方程。簡而言之,我們會先定義一個卡爾曼增益?
? ? ? ? ? ? ? ? ? ? ? ? ??
在卡爾曼增益的基礎上,后驗概率的形式為
? ? ?
? ? ? ?卡爾曼濾波器給出了在線性化之后狀態變量分布的變化過程。在線性系統和高斯噪聲下,卡爾曼濾波器給出了無偏最優估計。而在SLAM這種非線性的情況下,它給出了單次線性近似下的最大后驗估計。
2.EKF討論
? ? ? ?EKF形式簡潔、應用廣泛著稱。當想要在某段時間內估計某個不確定量時,我們首先想到的就是EKF。在早期的SLAM中,EKF占據了很長一段時間的主導地位,研究者們討論了各種各樣的濾波器在SLAM中的應用,如IF(信息濾波器)、IKF(Iterated KF)、UKF(Unscented KF)和粒子濾波器、SWF(Sliding Window Filter)等等,或者用分治法等思路改進EKF的效率。時至今日,盡管我們認識到非線性優化比濾波器占有明顯的優勢,但是在計算資源受限,或待估計量比較簡單的場合,EKF仍不失為一種有效的方式。
EKF有哪些局限呢?
(1)濾波器方法在一定程度上假設了馬爾可夫性,也就是時刻的狀態只與時刻相關,而與之前的狀態和觀測都無關(或者和前幾個有限時刻的狀態相關)。這有點像是在視覺里程計中只考慮相鄰兩幀的關系。如果當前幀確實與很久之前的數據有關(例如回環),那么濾波器會難以處理。而非線性優化方法則傾向于使用所有的歷史數據。它不光考慮鄰近時刻的特征點與軌跡關系,更會把很久之前的狀態也考慮進來,稱為全體時間上的SLAM(Full-SLAM)。在這種意義下,非線性優化方法使用了更多信息,當然也需要更多的計算。
(2)與第6講介紹的優化方法相比,EKF濾波器僅在處做了一次線性化,就直接根據這次線性化的結果,把后驗概率給算了出來。這相當于在說,我們認為該點處的線性化近似在后驗概率處仍然是有效的。而實際上,當我們離工作點較遠時,一階泰勒展開并不一定能夠近似整個函數,這取決于運動模型和觀測模型的非線性情況。如果它們有強烈的非線性,那么線性近似就只在很小范圍內成立,不能認為在很遠的地方仍能用線性來近似。這就是EKF的非線性誤差,也是它的主要問題所在。在優化問題中,盡管我們也做一階(最速下降)或二階(高斯牛頓法或列文伯格一馬夸爾特方法)的近似,但每迭代一次,狀態估計發生改變之后,我們會重新對新的估計點做泰勒展開,而不像EKF那樣只在固定點上做一次泰勒展開。這就使得優化的方法適用范圍更廣,在狀態變化較大時也能適用。所以大體來說,可以粗略地認為EKF僅是優化中的一次迭代R。(3)從程序實現上來說,EKF需要存儲狀態量的均值和萬差,并對它們進行維護和更新。如
果把路標也放進狀態,由于視覺SLAM 中路標數量很大,則這個存儲重是相當可觀的,且與狀態量呈平方增長(因為要存儲協方差矩陣)。因此,普遍認為EKF SLAM個適用于大型場景。
(4)EKF等濾波器方法沒有異常檢測機制,導致系統在存在異常值的時候很容易發散。而在視覺SLAM 中,異常值卻是很常見的:無論特征匹配還是光流法,都容易追蹤或匹配到錯誤的點。沒有異常值檢測機制會讓系統在實用中非常不穩定? ? ? ?由于EKF存在這些明顯的缺點,我們通常認為,在同等計算量的情況下,非線性優化能取得更好的效果。這里“更好”是指精度和魯棒性同時達到更好的意思。下面我們來討論以非線性優化為主的后端。
9.2 BA與圖優化
? ? ? ?所謂的Bundle Adjustment(BA),是指從視覺圖像中提煉出最優的3D模型和相機參數(內參數和外參數)。考慮從任意特征點發射出來的幾束光線(bundles of light rays),它們會在幾個相機的成像平面上變成像素或是檢測到的特征點。如果我們調整(adjustment)各相機姿態和各特征點的空間位置,使得這些光線最終收束到相機的光心,就稱為BA。
? ? ? ?我們在第5講和第7講已經簡單介紹過BA的原理,本節的重點是介紹它對應的圖模型結構的特點,然后介紹一些通用的快速求解方法。
9.2.1 投影模型和BA代價函數
1.投影過程
? ? ? ?從一個世界坐標系中的點p出發,把相機的內外參數和畸變都考慮進來,最后投影成像素坐標,需要如下步驟:
(1)把世界坐標轉換到相機坐標,這里將用到相機外參數(R,t)??????? ? ?
? ? ? ? ? ? ? ? ? ? ? ? ? ??
? ???????? ? ? ? ???????? ? ? ? ???????? ? ? ? ???????? ? ? ? ?
(2)將
投至歸一化平面,得到歸一化坐標
? ? ? ? ? ? ? ? ??
(3)考慮歸一化坐標的畸變情況,得到去畸變前的原始像素坐標。這里暫時只考慮徑向畸變
?? ? ? ? ? ? ? ? ? ? ? ? ? ?
?(4)根據內參模型,計算像素坐標
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??
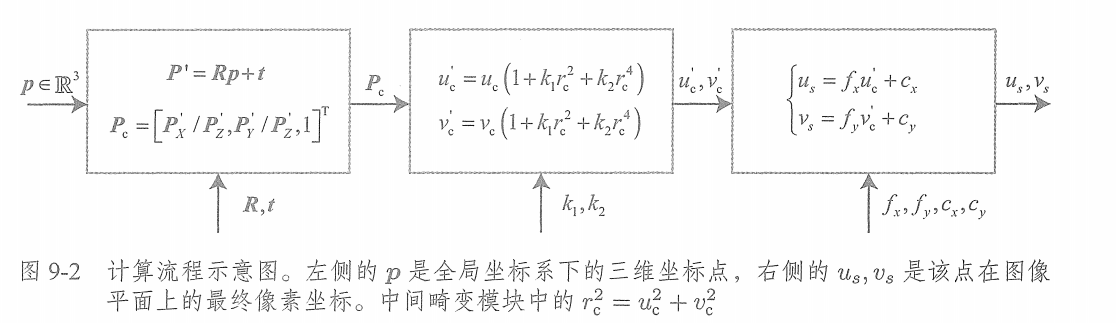
? ? ? ?這一系列計算流程看似復雜。我們用流程圖(如下)表示整個過程。讀者應該能領會到,這個過程也就是前面講的觀測方程,之前我們把它抽象地記成
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??
? ? ? ?現在,我們給出了它的詳細參數化過程。具體地說,這里的x指代此時相機的位姿,即外參R,t,它對應的李群為T,李代數為。路標y即這里的三維點p,而觀測數據則是像素坐標
。以最小二乘的角度來考慮,那么可以列寫關于此次觀測的誤差
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??
? ? ? ?然后,把其他時刻的觀測量也考慮進來,我們可以給誤差添加一個下標。設
為在位姿
處觀察路標
產生的數據,那么整體的代價函數為
? ? ? ? ?
? ? ? ?對這個最小二乘進行求解,相當于對位姿和路標同時做了調整,也就是所謂的BA。接下來,我們會根據該目標函數和第6講介紹的非線性優化內容,逐步深入地探討該模型的求解。
9.2.2 BA的求解
? ? ? ?觀察9.2.1節中的觀測模型h(T,p),很容易判斷該函數不是線性函數。所以我們希望使用6.2節介紹的一些非線性優化手段來優化它。
? ? ? ?根據非線性優化的思想,我們應該從某個初始值開始,不斷地尋找下降方向
,來找到目標函數的最優解,即不斷地求解增量方程中的增量
。盡管誤差項都是針對單個位姿和路標點的,但在整體BA目標函數上,我們應該把自變量定義成所有待優化的變量
? ? ? ? ? ? ? ? ? ? ? ? ? ?
? ? ? ?本節用高斯牛頓法進行優化,高斯牛頓法的核心就是求解J矩陣,即代價函數對每個待優化變量求偏導數。? ? ? ?增量方程中的
則是對整體自變量的增量。在這個意義下,當我們給自變量一個增量時,目標函數變為
? ? ? ?其中,表示整個代價函數在當前狀態下對相機姿態的偏導數,而
表示該函數對路標點位置的偏導。現在,把相機位姿變量放在一起
? ? ? ? ? ? ? ? ? ? ? ? ? ?
?并把空間點的變量也放在一起
? ? ? ? ? ? ? ? ? ? ? ? ??
那么,上式可簡化為
? ? ? ??
? ? ? ?需要注意的是,該式從一個由很多個小型二次項之和,變成矩陣形式。這里的雅可比矩陣和必須是整體目標函數對整體變量的導數,它將是一個很大塊的矩陣,而里頭每個小分塊,需要由每個誤差項的導數和拼湊”起來。然后,無論我們使用高斯牛頓法還是列文伯格一馬夸爾特方法,最后都將面對增量線性方程? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??
? ? ? ?根據第6講的知識,我們知道高斯牛頓法和列文伯格—馬夸爾特方法的主要差別在于,這里的H是取
還是
的形式。由于我們把變量歸類成了位姿和空間點兩種,所以雅可比矩陣可以分塊為
那么,以高斯牛頓法為例,則H矩陣為
? ? ? ? ? ? ? ? ? ? ? ? ?
? ? ? ? 當然,在列文伯格一馬夸爾特方法中我們也需要計算這個矩陣。不難發現,因為考慮了所有的優化變量,所以這個線性方程的維度將非常大,包含了所有的相機位姿和路標點。尤其是在視覺SLAM中,一幅圖像會提出數百個特征點,大大增加了這個線性方程的規模。如果直接對H求逆來計算增量方程,由于矩陣求逆是復雜度為的操作,那么消耗的計算資源會非常多。但這里的矩陣是有一定的特殊結構的。利用這個特殊結構,我們可以加速求解過程。
9.2.3 稀疏性和邊緣化
? ? ? ?H矩陣的稀疏性是由雅可比矩陣
引起的。考慮這些代價函數當中的其中一個
。注意,這個誤差項只描述了在
看到???????
這件事,只涉及第i個相機位姿和第j個路標點,對其余部分的變量的導數都為0。所以該誤差項對應的雅可比矩陣有下面的形式
? ? ? ?這個誤差項的雅可比矩陣,除了這兩處為非零塊,其余地方都為零。這體現了該誤差項與其他路標和軌跡無關的特性。從圖優化角度來說,這條觀測邊只和兩個頂點有關。那么,它對增量方程有何影響?H矩陣為什么會產生稀疏性呢?
9.3 實踐:CeresBA
1.bundle_adjustment_ceres.cpp
#include <iostream>
#include <ceres/ceres.h>
#include "common.h"
#include "SnavelyReprojectionError.h"using namespace std;void SolveBA(BALProblem &bal_problem);int main(int argc, char **argv) {if (argc != 2) {cout << "usage: bundle_adjustment_ceres bal_data.txt" << endl;return 1;}BALProblem bal_problem(argv[1]);bal_problem.Normalize();// bal_problem.Perturb(0.1, 0.5, 0.5);bal_problem.WriteToPLYFile("initial.ply");SolveBA(bal_problem);bal_problem.WriteToPLYFile("final.ply");return 0;
}void SolveBA(BALProblem &bal_problem) {const int point_block_size = bal_problem.point_block_size();const int camera_block_size = bal_problem.camera_block_size();double *points = bal_problem.mutable_points();double *cameras = bal_problem.mutable_cameras();// Observations is 2 * num_observations long array observations// [u_1, u_2, ... u_n], where each u_i is two dimensional, the x// and y position of the observation.const double *observations = bal_problem.observations();ceres::Problem problem;for (int i = 0; i < bal_problem.num_observations(); ++i) {ceres::CostFunction *cost_function;// Each Residual block takes a point and a camera as input// and outputs a 2 dimensional Residualcost_function = SnavelyReprojectionError::Create(observations[2 * i + 0], observations[2 * i + 1]);// If enabled use Huber's loss function.ceres::LossFunction *loss_function = new ceres::HuberLoss(1.0);// Each observation corresponds to a pair of a camera and a point// which are identified by camera_index()[i] and point_index()[i]// respectively.double *camera = cameras + camera_block_size * bal_problem.camera_index()[i];double *point = points + point_block_size * bal_problem.point_index()[i];problem.AddResidualBlock(cost_function, loss_function, camera, point);}// show some information here ...std::cout << "bal problem file loaded..." << std::endl;std::cout << "bal problem have " << bal_problem.num_cameras() << " cameras and "<< bal_problem.num_points() << " points. " << std::endl;std::cout << "Forming " << bal_problem.num_observations() << " observations. " << std::endl;std::cout << "Solving ceres BA ... " << endl;ceres::Solver::Options options;options.linear_solver_type = ceres::LinearSolverType::SPARSE_SCHUR;options.minimizer_progress_to_stdout = true;ceres::Solver::Summary summary;ceres::Solve(options, &problem, &summary);std::cout << summary.FullReport() << "\n";
}
2.SnavelyReprojectionError.h
#ifndef SnavelyReprojection_H
#define SnavelyReprojection_H#include <iostream>
#include "ceres/ceres.h"
#include "rotation.h"class SnavelyReprojectionError {
public:SnavelyReprojectionError(double observation_x, double observation_y) : observed_x(observation_x),observed_y(observation_y) {}template<typename T>bool operator()(const T *const camera,const T *const point,T *residuals) const {// camera[0,1,2] are the angle-axis rotationT predictions[2];CamProjectionWithDistortion(camera, point, predictions);residuals[0] = predictions[0] - T(observed_x);residuals[1] = predictions[1] - T(observed_y);return true;}// camera : 9 dims array// [0-2] : angle-axis rotation// [3-5] : translateion// [6-8] : camera parameter, [6] focal length, [7-8] second and forth order radial distortion// point : 3D location.// predictions : 2D predictions with center of the image plane.template<typename T>static inline bool CamProjectionWithDistortion(const T *camera, const T *point, T *predictions) {// Rodrigues' formulaT p[3];AngleAxisRotatePoint(camera, point, p);// camera[3,4,5] are the translationp[0] += camera[3];p[1] += camera[4];p[2] += camera[5];// Compute the center fo distortionT xp = -p[0] / p[2];T yp = -p[1] / p[2];// Apply second and fourth order radial distortionconst T &l1 = camera[7];const T &l2 = camera[8];T r2 = xp * xp + yp * yp;T distortion = T(1.0) + r2 * (l1 + l2 * r2);const T &focal = camera[6];predictions[0] = focal * distortion * xp;predictions[1] = focal * distortion * yp;return true;}static ceres::CostFunction *Create(const double observed_x, const double observed_y) {return (new ceres::AutoDiffCostFunction<SnavelyReprojectionError, 2, 9, 3>(new SnavelyReprojectionError(observed_x, observed_y)));}private:double observed_x;double observed_y;
};#endif // SnavelyReprojection.h
3.CMakeLists.txt
#聲明要求cmake的最低版本
cmake_minimum_required(VERSION 3.16)#聲明一個cmake工程
project(slam_09)#啟用最高優化級別,移除調試開銷
set(CMAKE_BUILD_TYPE "Release")
#并行計算,加速運算
#add_definitions("-DENABLE_SSE")
# 啟用C++11
set(CMAKE_CXX_FLAGS "-O3 -std=c++11")LIST(APPEND CMAKE_MODULE_PATH ${PROJECT_SOURCE_DIR}/cmake)# 用標準方式指定 C++ 標準,別再手寫 -std=...
set(CMAKE_CXX_STANDARD 17)
set(CMAKE_CXX_STANDARD_REQUIRED ON)# 其它優化旗標可保留,但不要再含 -std=...
set(CMAKE_CXX_FLAGS "${CMAKE_CXX_FLAGS} -O3 -march=native -g")# Ceres
Find_Package(Ceres REQUIRED)
include_directories(${OpenCV_INCLUDE_DIRS})# Sophus
set(EIGEN3_INCLUDE_DIR "/usr/local/include/eigen3")
include_directories(${EIGEN3_INCLUDE_DIR})# g2o
list( APPEND CMAKE_MODULE_PATH /home/caohao/g2o/cmake_modules )
find_package(G2O REQUIRED)
SET(G2O_LIBS g2o_csparse_extension g2o_stuff g2o_core cxsparse)
include_directories(${G2O_INCLUDE_DIRS})#Eigen
Find_Package(Eigen3 REQUIRED)
include_directories(${EIGEN3_INCLUDE_DIRS})#CSparse
Find_Package(CSparse REQUIRED)
include_directories(${CSPARSE_INCLUDE_DIRS} /usr/include/suitesparse) # 添加一個可執行程序,可執行文件名 cpp文件名
add_library(bal_common common.cc)
add_executable(bundle_adjustment_g2o bundle_adjustment_g2o.cpp)
target_link_libraries(bundle_adjustment_g2o ${G2O_LIBS} bal_common)add_executable(bundle_adjustment_ceres bundle_adjustment_ceres.cpp)
target_link_libraries(bundle_adjustment_ceres ${CERES_LIBRARIES} bal_common)4.運行結果
caohao@ubuntu:~/桌面/slam/slam_09/build$ ./bundle_adjustment_ceres ../problem-16-22106-pre.txt
Header: 16 22106 83718
bal problem file loaded...
bal problem have 16 cameras and 22106 points.
Forming 83718 observations.
Solving ceres BA ...
iter cost cost_change |gradient| |step| tr_ratio tr_radius ls_iter iter_time total_time0 5.449147e+12 0.00e+00 3.24e+26 0.00e+00 0.00e+00 1.00e+04 0 9.38e-02 2.93e-011 7.421971e+16 -7.42e+16 0.00e+00 4.29e+04 -2.72e+04 5.00e+03 1 1.36e-01 4.29e-012 3.837108e+17 -3.84e+17 0.00e+00 3.47e+04 -1.41e+05 1.25e+03 1 1.13e-01 5.42e-013 1.202275e+14 -1.15e+14 0.00e+00 2.00e+04 -4.21e+01 1.56e+02 1 1.10e-01 6.52e-014 2.094139e+12 3.36e+12 1.45e+26 7.57e+03 1.23e+00 4.69e+02 1 1.90e-01 8.42e-015 1.715858e+15 -1.71e+15 0.00e+00 3.56e+04 -1.64e+03 2.34e+02 1 1.23e-01 9.66e-016 1.822053e+24 -1.82e+24 0.00e+00 2.53e+04 -1.74e+12 5.86e+01 1 1.34e-01 1.10e+007 1.586121e+13 -1.38e+13 0.00e+00 1.33e+04 -1.31e+01 7.32e+00 1 1.25e-01 1.22e+008 7.984580e+11 1.30e+12 6.40e+25 8.71e+03 1.24e+00 2.20e+01 1 1.92e-01 1.42e+009 3.717661e+11 4.27e+11 2.72e+25 3.49e+04 1.07e+00 6.59e+01 1 1.83e-01 1.60e+0010 1.397932e+11 2.32e+11 1.12e+25 1.54e+05 1.25e+00 1.98e+02 1 1.91e-01 1.79e+0011 7.927556e+10 6.05e+10 4.65e+24 4.29e+05 8.66e-01 3.25e+02 1 2.01e-01 1.99e+0012 2.985965e+10 4.94e+10 1.95e+24 8.55e+05 1.25e+00 9.76e+02 1 2.45e-01 2.24e+0013 1.467261e+13 -1.46e+13 0.00e+00 2.13e+06 -9.81e+02 4.88e+02 1 1.43e-01 2.38e+0014 4.564222e+11 -4.27e+11 0.00e+00 1.95e+06 -2.86e+01 1.22e+02 1 1.30e-01 2.51e+0015 8.197420e+10 -5.21e+10 0.00e+00 1.47e+06 -3.49e+00 1.52e+01 1 1.33e-01 2.64e+0016 6.408802e+11 -6.11e+11 0.00e+00 7.34e+05 -4.10e+01 9.53e-01 1 1.14e-01 2.76e+0017 1.305787e+10 1.68e+10 1.04e+24 1.85e+05 1.16e+00 2.86e+00 1 1.82e-01 2.94e+0018 2.524155e+10 -1.22e+10 0.00e+00 3.25e+05 -1.88e+00 1.43e+00 1 1.13e-01 3.05e+0019 5.170160e+10 -3.86e+10 0.00e+00 2.21e+05 -6.02e+00 3.57e-01 1 1.10e-01 3.16e+0020 6.704971e+09 6.35e+09 6.69e+23 8.71e+04 1.10e+00 1.07e+00 1 1.79e-01 3.34e+0021 2.840951e+09 3.86e+09 3.83e+23 1.64e+05 1.19e+00 3.22e+00 1 1.82e-01 3.52e+0022 4.867017e+09 -2.03e+09 0.00e+00 2.61e+05 -1.44e+00 1.61e+00 1 1.14e-01 3.64e+0023 4.306863e+09 -1.47e+09 0.00e+00 1.80e+05 -1.06e+00 4.02e-01 1 1.15e-01 3.75e+0024 6.444281e+10 -6.16e+10 0.00e+00 7.67e+04 -4.93e+01 5.03e-02 1 1.16e-01 3.87e+0025 2.292929e+09 5.48e+08 1.81e+23 1.37e+04 1.01e+00 1.51e-01 1 1.78e-01 4.05e+0026 1.428202e+12 -1.43e+12 0.00e+00 3.57e+04 -1.87e+03 7.54e-02 1 1.13e-01 4.16e+0027 1.737359e+09 5.56e+08 1.47e+23 1.95e+04 1.02e+00 2.26e-01 1 1.82e-01 4.34e+0028 1.026685e+09 7.11e+08 9.36e+22 4.82e+04 1.08e+00 6.79e-01 1 1.86e-01 4.53e+0029 5.007847e+08 5.26e+08 8.52e+22 1.01e+05 1.12e+00 2.04e+00 1 1.85e-01 4.71e+0030 7.339717e+08 -2.33e+08 0.00e+00 1.73e+05 -9.92e-01 1.02e+00 1 1.19e-01 4.83e+0031 2.216996e+08 2.79e+08 8.18e+22 1.15e+05 1.22e+00 3.05e+00 1 1.82e-01 5.02e+0032 1.344091e+08 8.73e+07 7.28e+22 1.97e+05 8.93e-01 5.93e+00 1 1.89e-01 5.20e+0033 1.119116e+09 -9.85e+08 0.00e+00 2.59e+05 -1.79e+01 2.96e+00 1 1.17e-01 5.32e+0034 6.409134e+07 7.03e+07 3.86e+22 1.72e+05 1.29e+00 8.89e+00 1 1.81e-01 5.50e+0035 1.704850e+08 -1.06e+08 0.00e+00 2.87e+05 -5.34e+00 4.45e+00 1 1.14e-01 5.62e+0036 1.387159e+20 -1.39e+20 0.00e+00 1.89e+05 -7.04e+12 1.11e+00 1 1.08e-01 5.72e+0037 4.409479e+07 2.00e+07 2.51e+22 8.27e+04 1.07e+00 3.33e+00 1 1.80e-01 5.90e+0038 7.478206e+07 -3.07e+07 0.00e+00 1.48e+05 -3.18e+00 1.67e+00 1 1.17e-01 6.02e+0039 3.260413e+07 1.15e+07 3.60e+22 9.54e+04 1.23e+00 5.00e+00 1 1.86e-01 6.21e+0040 3.340178e+07 -7.98e+05 0.00e+00 1.66e+05 -1.98e-01 2.50e+00 1 1.18e-01 6.33e+0041 2.788577e+07 4.72e+06 2.89e+22 1.05e+05 1.21e+00 7.50e+00 1 1.79e-01 6.50e+0042 3.434983e+10 -3.43e+10 0.00e+00 1.99e+05 -1.93e+04 3.75e+00 1 1.14e-01 6.62e+0043 5.636097e+07 -2.85e+07 0.00e+00 1.25e+05 -1.71e+01 9.38e-01 1 1.18e-01 6.74e+0044 2.624261e+07 1.64e+06 2.40e+22 5.11e+04 1.13e+00 2.81e+00 1 1.80e-01 6.92e+0045 2.530990e+07 9.33e+05 2.54e+22 9.99e+04 1.12e+00 8.44e+00 1 2.03e-01 7.12e+0046 2.482545e+07 4.84e+05 1.78e+22 1.86e+05 9.15e-01 1.97e+01 1 1.85e-01 7.30e+0047 3.309190e+07 -8.27e+06 0.00e+00 3.28e+05 -1.76e+01 9.83e+00 1 1.17e-01 7.42e+0048 2.467838e+07 1.47e+05 5.06e+20 1.99e+05 3.99e-01 9.75e+00 1 1.77e-01 7.60e+0049 4.326292e+08 -4.08e+08 0.00e+00 1.98e+05 -1.19e+03 4.88e+00 1 1.17e-01 7.72e+0050 2.512612e+07 -4.48e+05 0.00e+00 1.27e+05 -1.56e+00 1.22e+00 1 1.07e-01 7.82e+00Solver Summary (v 2.0.0-eigen-(3.4.0)-lapack-suitesparse-(5.1.2)-cxsparse-(3.1.9)-eigensparse-no_openmp)Original Reduced
Parameter blocks 22122 22122
Parameters 66462 66462
Residual blocks 83718 83718
Residuals 167436 167436Minimizer TRUST_REGIONSparse linear algebra library SUITE_SPARSE
Trust region strategy LEVENBERG_MARQUARDTGiven Used
Linear solver SPARSE_SCHUR SPARSE_SCHUR
Threads 1 1
Linear solver ordering AUTOMATIC 22106,16
Schur structure 2,3,9 2,3,9Cost:
Initial 5.449147e+12
Final 2.467838e+07
Change 5.449122e+12Minimizer iterations 51
Successful steps 24
Unsuccessful steps 27Time (in seconds):
Preprocessor 0.199083Residual only evaluation 1.030133 (50)Jacobian & residual evaluation 1.535440 (24)Linear solver 4.412791 (50)
Minimizer 7.626142Postprocessor 0.005908
Total 7.831134Termination: NO_CONVERGENCE (Maximum number of iterations reached. Number of iterations: 50.)
9.4 實踐:g2o求解BA
1.bundle_adjustment_g2o.cpp
#include <g2o/core/base_vertex.h>
#include <g2o/core/base_binary_edge.h>
#include <g2o/core/block_solver.h>
#include <g2o/core/optimization_algorithm_levenberg.h>
#include <g2o/solvers/csparse/linear_solver_csparse.h>
#include <g2o/core/robust_kernel_impl.h>
#include <iostream>#include "common.h"
#include "sophus/se3.hpp"using namespace Sophus;
using namespace Eigen;
using namespace std;/// 姿態和內參的結構
struct PoseAndIntrinsics {PoseAndIntrinsics() {}/// set from given data addressexplicit PoseAndIntrinsics(double *data_addr) {rotation = SO3d::exp(Vector3d(data_addr[0], data_addr[1], data_addr[2]));translation = Vector3d(data_addr[3], data_addr[4], data_addr[5]);focal = data_addr[6];k1 = data_addr[7];k2 = data_addr[8];}/// 將估計值放入內存void set_to(double *data_addr) {auto r = rotation.log();for (int i = 0; i < 3; ++i) data_addr[i] = r[i];for (int i = 0; i < 3; ++i) data_addr[i + 3] = translation[i];data_addr[6] = focal;data_addr[7] = k1;data_addr[8] = k2;}SO3d rotation;Vector3d translation = Vector3d::Zero();double focal = 0;double k1 = 0, k2 = 0;
};
/// 位姿加相機內參的頂點,9維,前三維為so3,接下去為t, f, k1, k2
class VertexPoseAndIntrinsics : public g2o::BaseVertex<9, PoseAndIntrinsics> {
public:EIGEN_MAKE_ALIGNED_OPERATOR_NEW;VertexPoseAndIntrinsics() {}virtual void setToOriginImpl() override {_estimate = PoseAndIntrinsics();}virtual void oplusImpl(const double *update) override {_estimate.rotation = SO3d::exp(Vector3d(update[0], update[1], update[2])) * _estimate.rotation;_estimate.translation += Vector3d(update[3], update[4], update[5]);_estimate.focal += update[6];_estimate.k1 += update[7];_estimate.k2 += update[8];}/// 根據估計值投影一個點Vector2d project(const Vector3d &point) {Vector3d pc = _estimate.rotation * point + _estimate.translation;pc = -pc / pc[2];double r2 = pc.squaredNorm();double distortion = 1.0 + r2 * (_estimate.k1 + _estimate.k2 * r2);return Vector2d(_estimate.focal * distortion * pc[0],_estimate.focal * distortion * pc[1]);}virtual bool read(istream &in) {}virtual bool write(ostream &out) const {}
};class VertexPoint : public g2o::BaseVertex<3, Vector3d> {
public:EIGEN_MAKE_ALIGNED_OPERATOR_NEW;VertexPoint() {}virtual void setToOriginImpl() override {_estimate = Vector3d(0, 0, 0);}virtual void oplusImpl(const double *update) override {_estimate += Vector3d(update[0], update[1], update[2]);}virtual bool read(istream &in) {}virtual bool write(ostream &out) const {}
};class EdgeProjection :public g2o::BaseBinaryEdge<2, Vector2d, VertexPoseAndIntrinsics, VertexPoint> {
public:EIGEN_MAKE_ALIGNED_OPERATOR_NEW;virtual void computeError() override {auto v0 = (VertexPoseAndIntrinsics *) _vertices[0];auto v1 = (VertexPoint *) _vertices[1];auto proj = v0->project(v1->estimate());_error = proj - _measurement;}// use numeric derivativesvirtual bool read(istream &in) {}virtual bool write(ostream &out) const {}};void SolveBA(BALProblem &bal_problem);int main(int argc, char **argv) {if (argc != 2) {cout << "usage: bundle_adjustment_g2o bal_data.txt" << endl;return 1;}BALProblem bal_problem(argv[1]);bal_problem.Normalize();bal_problem.Perturb(0.1, 0.5, 0.5);bal_problem.WriteToPLYFile("initial2.ply");SolveBA(bal_problem);bal_problem.WriteToPLYFile("final2.ply");return 0;
}void SolveBA(BALProblem &bal_problem) {const int point_block_size = bal_problem.point_block_size();const int camera_block_size = bal_problem.camera_block_size();double *points = bal_problem.mutable_points();double *cameras = bal_problem.mutable_cameras();// pose dimension 9, landmark is 3typedef g2o::BlockSolver<g2o::BlockSolverTraits<9, 3>> BlockSolverType;typedef g2o::LinearSolverCSparse<BlockSolverType::PoseMatrixType> LinearSolverType;// use LMauto solver = new g2o::OptimizationAlgorithmLevenberg(g2o::make_unique<BlockSolverType>(g2o::make_unique<LinearSolverType>()));g2o::SparseOptimizer optimizer;optimizer.setAlgorithm(solver);optimizer.setVerbose(true);/// build g2o problemconst double *observations = bal_problem.observations();// vertexvector<VertexPoseAndIntrinsics *> vertex_pose_intrinsics;vector<VertexPoint *> vertex_points;for (int i = 0; i < bal_problem.num_cameras(); ++i) {VertexPoseAndIntrinsics *v = new VertexPoseAndIntrinsics();double *camera = cameras + camera_block_size * i;v->setId(i);v->setEstimate(PoseAndIntrinsics(camera));optimizer.addVertex(v);vertex_pose_intrinsics.push_back(v);}for (int i = 0; i < bal_problem.num_points(); ++i) {VertexPoint *v = new VertexPoint();double *point = points + point_block_size * i;v->setId(i + bal_problem.num_cameras());v->setEstimate(Vector3d(point[0], point[1], point[2]));// g2o在BA中需要手動設置待Marg的頂點v->setMarginalized(true);optimizer.addVertex(v);vertex_points.push_back(v);}// edgefor (int i = 0; i < bal_problem.num_observations(); ++i) {EdgeProjection *edge = new EdgeProjection;edge->setVertex(0, vertex_pose_intrinsics[bal_problem.camera_index()[i]]);edge->setVertex(1, vertex_points[bal_problem.point_index()[i]]);edge->setMeasurement(Vector2d(observations[2 * i + 0], observations[2 * i + 1]));edge->setInformation(Matrix2d::Identity());edge->setRobustKernel(new g2o::RobustKernelHuber());optimizer.addEdge(edge);}optimizer.initializeOptimization();optimizer.optimize(40);// set to bal problemfor (int i = 0; i < bal_problem.num_cameras(); ++i) {double *camera = cameras + camera_block_size * i;auto vertex = vertex_pose_intrinsics[i];auto estimate = vertex->estimate();estimate.set_to(camera);}for (int i = 0; i < bal_problem.num_points(); ++i) {double *point = points + point_block_size * i;auto vertex = vertex_points[i];for (int k = 0; k < 3; ++k) point[k] = vertex->estimate()[k];}
}2.運行結果
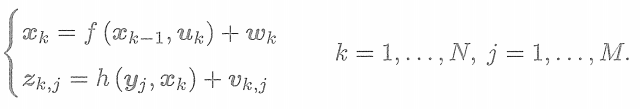
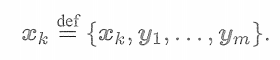
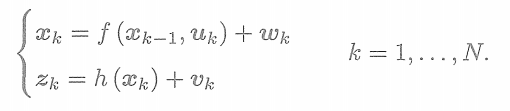
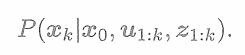
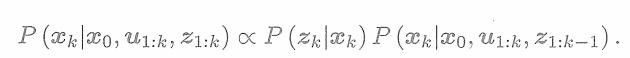
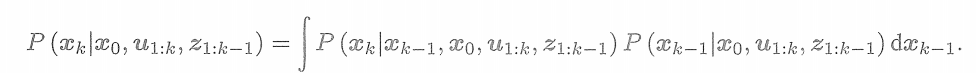
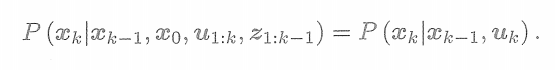
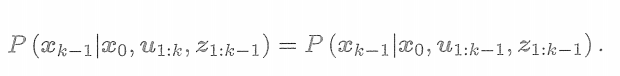
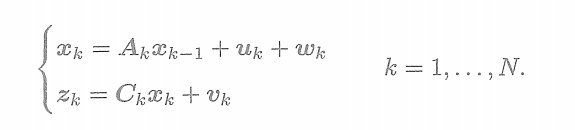
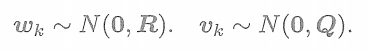
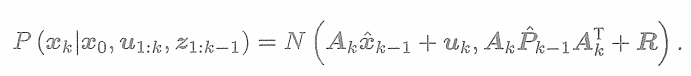
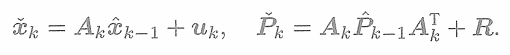
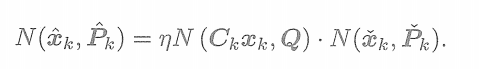
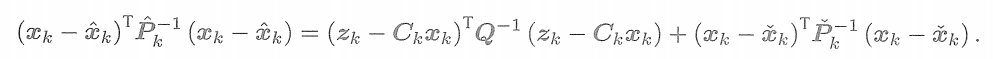
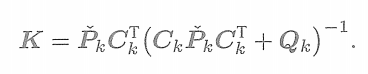
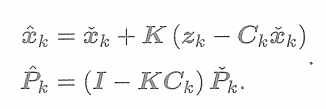
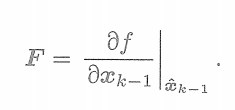
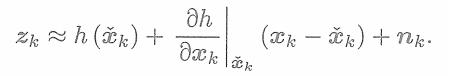
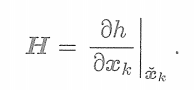
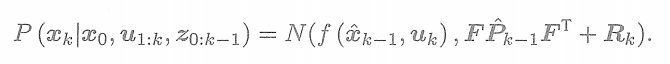
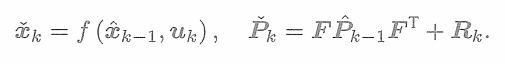
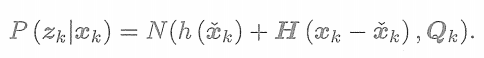
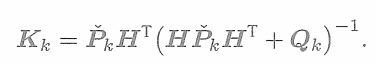
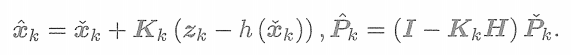
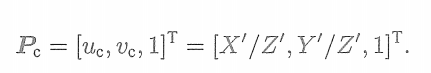
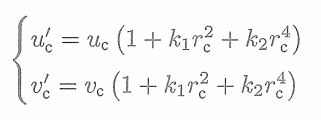
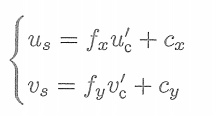
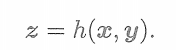
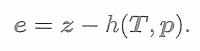
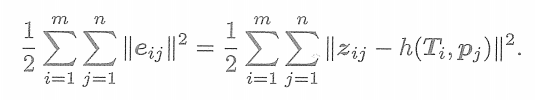
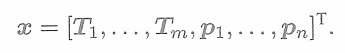
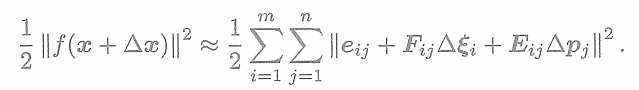

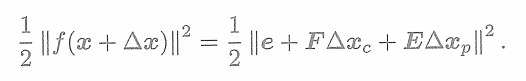
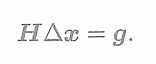
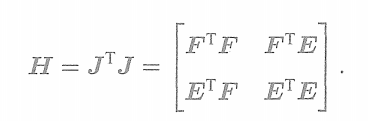
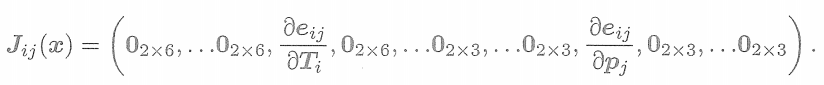



)
方法論))
)







)




模式可以在不修改對象外觀和功能的情況下添加或者刪除對象功能)

