算法與數據結構實戰技巧：從復雜度分析到數學優化

引言：為什么算法能力決定你的代碼“天花板”

作為程序員，你是否曾遇到這樣的困惑：同樣是處理數據，別人的代碼能輕松扛住10萬并發請求，而你的系統在1萬數據量時就開始卡頓甚至崩潰？這背后的差距，往往不在于編程語言的選擇或框架的新舊，而在于對算法與數據結構的理解深度。

在實際開發中，很多人習慣用“能跑就行”的標準衡量代碼質量，卻忽略了隱藏在運行效率背后的核心邏輯。當數據規模小時，暴力循環或許能應付；但隨著用戶量增長、業務復雜度提升，算法的優劣直接決定了系統的性能天花板。一個用哈希表（O(1)查詢）優化的緩存系統，和一個用數組遍歷（O(n)查詢）實現的版本，在百萬級數據面前會呈現天壤之別的響應速度。

核心問題：為什么看似功能相同的代碼，在面對大規模數據時會出現性能鴻溝？答案就藏在算法的時間復雜度、空間復雜度設計，以及數據結構的合理選型中。本文將從基礎概念拆解到實戰優化思路，用“接地氣”的方式幫你掌握提升代碼性能的關鍵技巧，讓你的程序從“能用”進化到“能扛”。

無論是求職面試中的算法題，還是工作中面對的性能瓶頸，算法能力都是程序員不可繞開的核心競爭力。接下來，我們將一步步揭開復雜度分析的面紗，探索數據結構的優化奧秘，讓你真正理解：好的算法，是寫出“抗打”代碼的前提。

算法的定義與本質：不止于“步驟”的解題邏輯

算法的通俗定義：從“菜譜”到“解題步驟”

提到“算法”，你可能會聯想到復雜的代碼或高深的數學公式，但其實它就藏在我們的日常生活里——比如你每天做飯時遵循的菜譜，就是一套完美的“算法原型”。

用“菜譜邏輯”拆解算法本質

想象你要做一道番茄炒蛋：首先需要準備番茄、雞蛋、調料（輸入），然后按步驟完成切菜、熱鍋、翻炒、調味（處理），最終得到一盤色香味俱全的菜品（輸出）。這個“食材→步驟→成品”的流程，正是算法的核心框架。

但算法比普通菜譜多了兩個關鍵約束：

有限步驟：必須在確定次數內完成。就像菜譜會明確“翻炒3分鐘”，而不是“炒到天荒地老”。
確定性：每一步指令必須清晰無歧義。如果菜譜寫“加鹽少許”，可能會讓新手困惑；但算法會精確到“加鹽5克”，確保無論誰執行都能得到相同結果。

算法的黃金法則：
? 必須有明確的輸入和輸出
? 步驟有限且可執行
? 每步指令清晰無歧義

反例：為什么“隨機試密碼”不是算法？

假設你忘記了手機密碼，打算隨機嘗試組合——這種方式永遠不能稱為算法。因為密碼可能有10000種組合（4位數字），極端情況下需要嘗試到最后一次才能成功，步驟數量是“潛在無限”的。而算法的本質是“用有限步驟解決問題”，就像菜譜絕不會讓你“無限嘗試火候直到菜熟”。

通過這個類比你會發現：算法其實是“解決問題的標準化流程”，它像菜譜一樣讓復雜任務變得可操作，又比菜譜更嚴謹可靠。下一次當你聽到“算法”時，不妨想想廚房里的那些步驟——它們背后藏著相同的邏輯智慧。

算法的核心特征：判斷“好算法”的四把標尺

作為程序員，我們每天都在與算法打交道，但你是否思考過：一個“合格”的算法究竟要具備哪些核心特質？學術定義中的算法特征往往抽象難懂，今天我們就從實戰角度，用四把“程序員標尺”拆解算法的必備素質，并結合經典的“兩數之和”問題，看看這些特征如何在代碼中落地。

一、四把標尺：從學術定義到代碼實踐

算法的本質是“解決問題的步驟”，但不是所有步驟都能稱為算法。從程序員視角看，一個可靠的算法必須滿足以下四個核心特征：

算法四特征·程序員版

明確輸入輸出：像函數定義一樣，有清晰的“原材料”（參數）和“成品”（返回值）
步驟有限性：不會陷入無限循環，執行次數有明確邊界
每步確定性：邏輯分支（如if-else）清晰無歧義，計算機能“看懂”
可行性：能用代碼實現，不依賴“理論上存在但工程不可行”的步驟

二、代碼實例：“兩數之和”如何體現四特征？

以LeetCode經典題目“兩數之和”為例（給定整數數組nums和目標值target，返回和為target的兩個元素下標），我們用暴力解法代碼逐一標注這些特征：

python

def twoSum(nums, target):# 遍歷數組中每個元素（i為第一個數下標）for i in range(len(nums)):# 遍歷i之后的元素（j為第二個數下標，避免重復計算）for j in range(i + 1, len(nums)):# 判斷兩數之和是否等于目標值if nums[i] + nums[j] == target:return [i, j]  # 找到則返回下標對return []  # 無結果時返回空列表

1. 明確輸入輸出：函數的“契約精神”

代碼中def twoSum(nums, target):定義了輸入為數組nums（待查找的數字集合）和整數target（目標和），返回值為整數數組[i, j]（滿足條件的下標對）。這種“參數→返回值”的明確對應，就像工廠的“原料入口”和“產品出口”，是算法可復用的基礎。

2. 步驟有限性：拒絕“無限循環”陷阱

外層循環for i in range(len(nums))和內層循環for j in range(i + 1, len(nums))嚴格限制了執行次數：假設數組長度為n，外層循環最多執行n次，內層循環最多執行n-1次，總步驟數不超過n*(n-1)/2。即使面對空數組或無結果的情況，也會在遍歷完所有可能后返回[]，絕不會陷入“死循環”。

3. 每步確定性：計算機的“導航圖”

代碼中所有邏輯分支都清晰無歧義：

循環變量i和j的取值范圍由range()嚴格定義，沒有“可能取這個值也可能取那個值”的模糊性；
條件判斷if nums[i] + nums[j] == target是明確的布爾表達式，結果非真即假，計算機能精準執行“返回下標”或“繼續循環”的操作。
這種“步步有依據”的特性，確保算法不會“迷路”。

4. 可行性：從想法到代碼的“落地能力”

整個邏輯用Python實現，無需依賴任何理論上的“理想條件”（如無限內存、超高速計算）。即使是初學者，也能通過編譯器將這段代碼轉化為可執行程序，在普通電腦上處理長度為1000的數組——這正是“可行性”的核心：算法必須能被工程化實現，而不是停留在紙面上的空想。

三、總結：四把標尺的實戰意義

判斷一個算法是否“合格”，本質是判斷它能否穩定、高效、無歧義地解決問題。明確輸入輸出確保算法“知道要做什么”，步驟有限性保證“不會做不完”，每步確定性確保“不會做錯”，可行性則讓“想法變成現實”。這四把標尺不僅是理論要求，更是我們日常寫代碼時排查bug的“ checklist ”——比如當代碼陷入死循環，很可能是“步驟有限性”出了問題；當函數返回值混亂，往往是“輸入輸出定義”不清晰。

下次寫算法時，不妨用這四把標尺“量一量”，你會發現：好算法的本質，就是把復雜問題拆解成計算機能理解的“確定性步驟”。

數據結構：算法的“舞臺”，效率的“隱形推手”

數據結構的本質：數據的“收納方式”

想象你走進一家倉庫，貨架上的物品擺放方式直接決定了你找到目標商品的速度——這就是數據結構的本質：數據的“收納藝術”。就像按編號整齊排列的抽屜能讓你瞬間定位物品，而雜亂堆放的箱子需要逐個翻找，不同的數據結構通過對數據的組織方式，深刻影響著算法操作的效率1。

兩種經典“收納方案”的對決

數組（順序存儲） 如同超市貨架上按編號排列的商品，所有數據在內存中連續存放，每個元素都有固定的“位置編號”（索引）。這種結構的最大優勢是 隨機訪問 ——無論數據量多大，只要知道索引，就能像打開指定編號的抽屜一樣直接獲取數據，時間復雜度為 O(1)。比如要找第 5 個元素，直接通過 arr[4]（假設從 0 開始計數）即可完成，無需遍歷其他元素。

鏈表（鏈式存儲） 則像掛在鉤子上的一串鑰匙，每個數據節點通過指針（或引用）連接下一個節點，內存中可以分散存放。這種“彈性連接”使其在 插入/刪除操作 上極具優勢：只需改變相鄰節點的指針指向，就像在鑰匙串中間加一把鑰匙只需解開前后連接，無需移動其他鑰匙，時間復雜度為 O(1)。但代價是查找時必須從頭節點開始逐個遍歷，直到找到目標，時間復雜度為 O(n)。

代碼片段直擊操作差異

我們通過 Python 偽代碼直觀對比“查找目標元素”的步驟差異：

數組查找（已知索引）：

python

def array_search(arr, index):# 直接通過索引訪問，一步到位return arr[index]# 使用示例：查找第3個元素（索引2）
result = array_search([10, 20, 30, 40], 2)  # 結果：30

鏈表查找（需從頭遍歷）：

python

class ListNode:def __init__(self, val=0, next=None):self.val = valself.next = nextdef linked_list_search(head, target):current = head# 必須從頭節點開始，逐個檢查下一個節點while current:if current.val == target:return currentcurrent = current.nextreturn None  # 未找到# 使用示例：查找值為30的節點
# 鏈表結構：10 -> 20 -> 30 -> 40
head = ListNode(10, ListNode(20, ListNode(30, ListNode(40))))
result = linked_list_search(head, 30)  # 需遍歷3個節點才找到

核心啟示：沒有“萬能收納法”，只有“場景適配”——當需要頻繁隨機訪問數據時（如數據庫索引），數組是最優解；當需要頻繁增刪節點時（如實時消息隊列），鏈表更具優勢。選擇數據結構的本質，就是在“空間占用”與“操作效率”之間找到平衡。

從倉庫管理到代碼世界，數據結構的“收納邏輯”始終不變：用對結構，效率倍增；選錯結構，事倍功半。理解這種底層邏輯，是寫出高性能代碼的第一步。

算法與數據結構：“演員”與“舞臺”的共生關系

如果把程序開發比作一場電影拍攝，那么算法就像演員的表演——它決定了“如何做”的邏輯流程；而數據結構則是舞臺布景，決定了“在哪里做”的基礎環境。就像優秀的舞臺設計能讓演員的表演更具張力，合適的數據結構也能讓算法效率得到質的飛躍。

以用戶信息查詢為例，當我們用哈希表存儲用戶數據時，通過鍵值對直接定位的特性，查詢效率能比傳統數組提升10倍。這種“好舞臺成就好表演”的案例，在實際開發中比比皆是。但反過來，如果選錯了“舞臺”，即便算法邏輯再精妙，也可能陷入“英雄無用武之地”的困境。

比如實現一個需要頻繁插入的隊列：若用數組作為底層數據結構，每次插入元素都需要移動后續所有元素，時間復雜度為O(n)；而改用鏈表實現時，只需調整指針指向，插入操作可在O(1)時間內完成。這個對比生動說明：數據結構不是算法的附屬品，而是決定其發揮空間的關鍵框架。

核心啟示：算法與數據結構的關系，本質是“邏輯”與“載體”的共生。就像電影需要根據劇情選擇實景拍攝還是綠幕特效，開發者也必須根據業務場景（如查詢頻率、插入需求）選擇匹配的數據結構，才能讓算法真正釋放價值。

無論是提升10倍效率的哈希表，還是O(n)與O(1)的性能鴻溝，都在印證同一個道理：在程序世界里，沒有絕對“好”的算法，只有與數據結構“適配”的解決方案。理解這種共生關系，正是從“會寫代碼”到“寫好代碼”的關鍵一步。

復雜度分析：衡量算法效率的“通用語言”

時間復雜度：算法“跑多快”的量化指標

為什么同樣處理1000條數據，有的程序瞬間完成，有的卻要卡頓幾秒？這背后的核心差異，就藏在時間復雜度這個算法的“速度密碼”里。它不關心你用的是最新款電腦還是老舊手機，只專注于一個問題：當數據量（專業上稱為“問題規模n”）增長時，算法的執行次數會如何變化。

時間復雜度的本質：用“執行次數隨問題規模n的增長趨勢”來衡量算法效率，忽略硬件性能、編程語言等外部因素，只關注核心的數學規律。比如處理100條數據時執行100次，處理1000條時執行1000次，這種“n增長多少倍，執行次數就增長多少倍”的規律，就是時間復雜度要捕捉的核心。

用大O符號給算法“測速”

描述時間復雜度時，我們通常用大O符號（O(f(n))），其中f(n)是問題規模n的函數。這個符號像一把“效率標尺”，告訴我們當n足夠大時，算法執行次數的增長上限。比如：

O(1)：常數時間，執行次數不隨n變化，像數學里的“常數函數”
O(n)：線性時間，執行次數和n成正比，像“一次函數”
O(log n)：對數時間，執行次數隨n增長但增速緩慢，像“對數函數”
O(n log n)：線性對數時間，n和log n的乘積
O(n2)：平方時間，執行次數是n的平方，像“二次函數”

這些符號看似抽象，其實在生活中隨處可見。我們用“快遞分揀”的場景來拆解它們：

快遞分揀員的“復雜度課堂”

假設你是倉庫分揀員，面前有n個快遞包裹，該如何高效找到目標包裹？不同策略對應不同時間復雜度：

O(1)：直接定位貨架
如果每個快遞都有唯一編號，且貨架按編號分區（比如A區放1-100號，B區放101-200號），你可以直接走到對應貨架拿起包裹。無論n是100還是10000，你都只需要1步——這就是常數時間，執行次數和n無關。
O(n)：逐個翻找所有包裹
如果包裹雜亂堆放，沒有編號規律，你只能從第一個開始逐個檢查，直到找到目標。運氣差時要翻完所有n個包裹——這就是線性時間，執行次數隨n線性增長。
O(log n)：二分查找編號
如果包裹按編號從小到大排列，你可以用“猜數字”的思路：先看中間包裹的編號，如果比目標小，就只查后半部分；如果比目標大，就只查前半部分。每次查找都能排除一半包裹，n=1000時最多只需10步（因為21?=1024）——這就是對數時間，執行次數隨n增長但增速極慢。

代碼里的“速度對決”：冒泡排序 vs 快速排序

理論講完，我們看實戰。同樣是給n個數排序，冒泡排序和快速排序的效率差異，正是時間復雜度的直觀體現：

冒泡排序（O(n2)）

核心思路是“相鄰元素比大小，小的往前冒”，需要兩層嵌套循環：

python

def bubble_sort(arr):n = len(arr)for i in range(n):  # 外層循環n次for j in range(0, n-i-1):  # 內層循環約n次if arr[j] > arr[j+1]:arr[j], arr[j+1] = arr[j+1], arr[j]

當n=1000時，執行次數約為1000×1000=10?次；n=10000時，直接飆升到10?次，時間隨n的平方爆炸增長。

快速排序（O(n log n)）

核心思路是“分而治之”，通過基準值將數組分成兩部分，遞歸排序：

python

def quick_sort(arr):if len(arr) <= 1:return arrpivot = arr[len(arr)//2]  # 選中間元素為基準left = [x for x in arr if x < pivot]  # 小于基準的部分middle = [x for x in arr if x == pivot]  # 等于基準的部分right = [x for x in arr if x > pivot]  # 大于基準的部分return quick_sort(left) + middle + quick_sort(right)  # 遞歸處理子數組

排序n個元素時，需要log n層遞歸（類似二分查找），每層處理n個元素，總執行次數約為n log n。n=10000時，執行次數約為10000×14≈1.4×10?次，僅為冒泡排序的1/700！

常見時間復雜度速查表

為了更清晰對比，我們整理了算法世界中最常見的復雜度類型、特征及適用場景：

復雜度類型	增長特征（n增大時）	典型場景
O(1)	執行次數恒定，不隨n變化	數組直接訪問、哈希表查找
O(log n)	增長緩慢，n翻倍時執行次數僅+1	二分查找、平衡二叉樹操作
O(n)	執行次數與n成正比	線性查找、單層循環遍歷
O(n log n)	增長適中，n log n級	快速排序、歸并排序、堆排序
O(n2)	增長迅速，n翻倍執行次數×4	冒泡排序、選擇排序、嵌套循環

關鍵結論：選擇算法時，優先關注復雜度的“數量級”。O(n log n)算法在n=10?時，效率可能是O(n2)算法的10萬倍！這就是為什么大廠面試總把復雜度分析作為“敲門磚”——它直接決定了系統能否扛住海量數據的沖擊。

通過時間復雜度，我們能穿透代碼表象，看到算法的“數學本質”。下一次優化程序時，不妨先問自己：這段代碼的執行次數，會隨著數據量增長如何變化？這或許就是從“寫對代碼”到“寫好代碼”的關鍵一步。

空間復雜度：算法“占多大地方”的衡量標準

當我們評價一個算法時，除了關注它“跑多快”，還得關心它“占多大地方”——這就是空間復雜度的核心意義。想象你整理衣柜：同樣是收納10件衣服，有人需要額外搬一個儲物箱（占用額外空間），有人卻能原地重新排列（不占額外空間），算法的空間占用差異與此類似。

空間復雜度的準確定義：算法在運行過程中額外占用的存儲空間，不包含輸入數據本身所需要的空間。這就像我們計算搬家成本時，只統計行李箱之外額外打包的紙箱體積，而不包括你原本要搬的家具。

常見的空間復雜度類型

實際開發中，我們最常遇到兩種空間復雜度：

O(1)：原地操作，空間恒定
這類算法就像“原地整理衣柜”，無論輸入數據規模多大，額外占用的空間始終不變。例如冒泡排序，它通過交換數組內部元素完成排序，整個過程只需要幾個臨時變量，空間復雜度就是O(1)。
O(n)：線性增長，按需分配
這類算法需要額外開辟與輸入規模成正比的空間。比如歸并排序，為了合并兩個有序子數組，需要創建一個臨時數組來存儲中間結果，輸入數據量翻倍時，臨時數組的大小也會翻倍，空間復雜度即為O(n)。

遞歸 vs 迭代：斐波那契數列的空間差異

最能體現空間復雜度差異的經典案例，莫過于斐波那契數列的兩種實現方式。我們以計算第n個斐波那契數為例，看看遞歸和迭代在空間占用上的天壤之別。

遞歸實現（空間復雜度O(n)）

遞歸方法通過不斷調用自身求解子問題，每一次遞歸調用都會在內存的“調用棧”中保存當前的函數狀態（包括參數、返回地址等）。當計算第n個斐波那契數時，調用棧的深度會達到n層，因此額外空間復雜度為O(n)。

python

def fib_recursive(n):if n <= 1:return n# 每次遞歸調用都會新增棧幀，棧深度為nreturn fib_recursive(n-1) + fib_recursive(n-2)

迭代實現（空間復雜度O(1)）

迭代方法則完全不同，它通過循環更新有限的變量來計算結果，整個過程只需要存儲前兩個數的值，無論n多大，額外空間始終是固定的3個變量（a, b, c），空間復雜度優化為O(1)。

python

def fib_iterative(n):if n <= 1:return na, b = 0, 1for _ in range(2, n+1):c = a + ba, b = b, c  # 僅更新變量，無額外空間增長return b

關鍵差異總結：遞歸實現因調用棧深度產生線性空間占用，而迭代實現通過“滾動更新”將空間壓縮到常數級別。這個對比揭示了算法設計的重要原則：有時通過改變實現方式，能在不影響功能的前提下大幅降低空間消耗。

這種空間優化的思路，也為我們后續討論“時間與空間的權衡”埋下伏筆——當內存資源有限時（如嵌入式設備、移動端開發），選擇迭代實現能避免遞歸可能導致的“棧溢出”風險；而在追求代碼簡潔性的場景，遞歸雖占用更多空間，卻可能讓邏輯更清晰。理解空間復雜度，正是做出這類技術決策的基礎。

時間復雜度優先的現實邏輯：用戶體驗“不等人”

想象一下電商平臺的秒殺場景：當你盯著屏幕等待搶購心儀商品時，10秒的加載時間足以讓你錯失機會，甚至直接關閉頁面——用戶對“即時性”的敏感度遠超想象。但很少有人會在意手機是512MB內存還是1GB內存，因為這類空間資源的差異在日常使用中幾乎無感。這就是為什么在算法設計中，時間復雜度往往比空間復雜度更值得優先考量：用戶體驗的核心訴求是“不等待”，而速度感知直接決定產品生死。

相比之下，空間資源的問題往往有更簡單的解決方案。硬盤不夠可以加容量，內存不足可以插內存條，這些硬件擴容手段能快速緩解空間壓力。但CPU的處理速度卻像一道“硬門檻”，被算法效率死死卡住。就像O(n2)這樣的低效算法，當數據量n達到10萬時，即便用上最頂級的服務器，也會因為需要執行1萬億次運算而陷入卡頓——此時硬件再好，也成了“巧婦難為無米之炊”。

真實案例印證：某支付系統曾因采用O(n2)算法，在用戶高峰期響應時間高達800ms，導致大量用戶投訴。團隊重構算法為O(n log n)后，響應時間驟降至50ms，用戶投訴率直接下降90%。這個數據清晰地說明：優化時間復雜度，本質上是在拯救用戶體驗。

從電商秒殺到支付結算，從社交媒體刷新到導航路線規劃，用戶對“瞬間響應”的期待從未改變。與其在硬件升級上投入無底洞，不如先審視算法是否存在“效率瓶頸”——畢竟，沒有用戶愿意為糟糕的時間體驗買單。

大思維視角：從偽代碼到問題建模的“降維打擊”

偽代碼：剝離細節，直擊問題本質

當程序員在白板上推演算法、團隊協作討論思路時，你是否見過這樣的場景：有人糾結于用 Python 的縮進還是 Java 的大括號，有人爭論變量命名該用 camelCase 還是 snake_case，卻沒人關注「這個邏輯到底能不能解決問題」？這正是偽代碼要破解的困局——用自然語言與代碼邏輯的混合體，剝離語法細節，讓注意力聚焦在算法的核心步驟上。

偽代碼的「極簡主義」表達

偽代碼就像算法的「草稿紙」，它不追求編譯通過，只在乎邏輯清晰。比如要實現「查找數組中最大值」這個經典問題，偽代碼可以這樣寫：

plaintext

function findMax(arr):max = arr[0]for i from 1 to len(arr)-1:if arr[i] > max:max = arr[i]return max

這段不到 10 行的文字，已經把解決問題的核心思路講得明明白白。你不需要考慮數組越界的語法處理（比如 Python 的 try-except 或 Java 的 ArrayIndexOutOfBoundsException），也不用糾結循環變量的聲明方式，只需專注「如何通過遍歷比較找到最大值」這一本質問題。

藏在偽代碼里的「三要素」

看似簡單的偽代碼，其實暗藏算法分析的關鍵信息。以 findMax 為例，我們能清晰拆解出三個核心參數：

算法邏輯：通過「初始化最大值為首個元素，遍歷剩余元素并更新最大值」的步驟，實現查找功能；
問題規模：用 len(arr) 直接體現輸入數據的大小，這是后續復雜度分析的基礎；
輸入量：明確接收數組 arr 作為輸入，界定了算法的適用范圍。

偽代碼的「驗證神器」作用：當你寫完這段偽代碼，很容易發現潛在問題——如果數組為空（len(arr) = 0），arr[0] 會直接報錯；如果數組只有一個元素，循環不會執行但結果正確。這種「快速暴露邊界條件」的能力，讓偽代碼成為算法設計的「第一關測試」，比直接寫代碼調試更高效。

為什么每個程序員都該掌握偽代碼？

偽代碼的價值，在于它構建了一個「通用語言層」：無論你熟悉 Python、C++ 還是 JavaScript，都能通過偽代碼快速理解他人思路；在面試推導算法時，用偽代碼展示邏輯比糾結語法錯誤更能體現思維能力；甚至在系統設計初期，用偽代碼勾勒核心流程，能幫團隊規避「為實現而實現」的陷阱。

說到底，寫偽代碼的過程，就是用「問題解決者」的視角重新審視需求——當你能用簡潔的邏輯描述清楚「如何做」，具體用什么語言實現，不過是水到渠成的事。

偽方法三參數：量化算法效率的“通用模型”

要理解算法效率的本質，我們需要一個能精確描述其執行時間規律的框架。偽方法三參數模型正是這樣一種工具，它將算法的執行時間定義為三個核心要素的函數：T(A, n, I) = 算法A在問題規模n、輸入I下的執行時間。這個簡潔的公式背后，藏著理解算法性能的關鍵邏輯。

用“快遞配送”理解三參數模型

如果把算法比作一場快遞配送任務，三個參數的含義會變得非常直觀：

A（算法策略）：對應快遞的配送方案。比如有的公司按區域劃分配送路線（類似排序算法中的“分治策略”），有的則按距離遠近優先配送（類似“貪心策略”），不同策略直接影響整體效率。
n（問題規模）：對應待配送的包裹總數。10個包裹和1000個包裹對配送時間的要求完全不同，這就像算法處理10條數據和100萬條數據時的性能差異。
I（輸入特性）：對應包裹的地址分布。如果所有包裹都集中在同一個小區（類似“已排序數組”），配送會很高效；如果地址分散在城市各個角落（類似“隨機無序數組”），則需要更多時間。

通過這個類比可以發現，算法的執行時間T并非固定值，而是由策略、規模和輸入特性共同決定的動態結果。

核心價值：偽方法模型的真正意義，在于幫我們剝離具體場景的干擾，聚焦最本質的問題——當問題規模n持續增大時，執行時間T會如何增長？ 這個增長規律，就是我們常說的“時間復雜度”。它像一把尺子，讓我們能在不依賴具體硬件環境的情況下，預判算法在大數據量下的表現，為后續深入分析CPU指令集層面的優化奠定理論基礎。

無論是評估排序算法的優劣，還是優化數據庫查詢效率，偽方法三參數模型都提供了一套通用的分析語言。它讓我們從“算法跑多快”的表象，深入到“算法為什么快/慢”的本質，這正是復雜度分析的起點。

CPU指令集與復雜度優化：為何數學模型是“王道”

CPU指令集：時間復雜度的“物理基礎”

想象一下，計算機的CPU就像一家精密運轉的工廠，而指令集則是這家工廠里固定不變的“生產工序”。每個指令都有明確的執行時間——比如加法指令可能耗時1ns，跳轉指令需要2ns，就像流水線上焊接工序需要3分鐘，質檢工序需要5分鐘一樣。

算法在CPU上的執行過程，本質就是調用這些“工序”的過程。它的總耗時可以用一個簡單公式計算：算法執行時間 = （加法指令次數×1ns）+（跳轉指令次數×2ns）+ ... 。所有指令的執行次數與各自耗時的乘積之和，構成了算法的真實運行成本。

我們用兩個經典例子來具體理解：

O(n)算法：假設它核心操作是執行n次加法，那么總耗時就是 n×1ns。當數據規模n翻倍時，耗時也會隨之翻倍。
O(n2)算法：如果核心操作是執行n2次加法，總耗時則為 n2×1ns。當n從100增加到200時，耗時會從10,000ns飆升到40,000ns，增長幅度遠超數據規模的變化。

核心洞察：時間復雜度分析的本質，正是對算法執行過程中指令集調用次數集合的抽象描述。它忽略了具體指令的耗時差異（比如1ns或2ns），只關注當數據規模n增長時，指令總執行次數的增長趨勢——這就是為什么O(n2)算法在大數據量下會比O(n)算法慢得多的“物理基礎”。

這種將復雜問題抽象為“次數集合”的思維，讓我們能在不依賴具體硬件的情況下，預判算法的效率瓶頸。就像工廠管理者不需要知道每臺機器的具體功率，只需通過工序數量的增長模式，就能判斷生產線能否應對訂單量的激增。

硬件優化的局限與數學模型的“優越性”

當系統性能遇到瓶頸時，你會先想到升級服務器配置，還是優化代碼邏輯？很多人下意識選擇前者，但硬件優化的“性價比陷阱” 往往被忽略——相比之下，數學模型與算法優化可能才是更可持續的解決方案。

硬件優化的三大“致命傷”

硬件升級看似直接，卻藏著難以逾越的障礙：

成本高企：更換CPU、擴容內存等硬件操作，成本通常是軟件優化的10倍以上。某電商平臺曾測算，通過硬件升級支持千萬級并發需投入上千萬元，而算法優化僅需重構核心模塊，成本不到百萬。

性能天花板觸手可及：CPU主頻從3GHz提升到4GHz僅帶來33%的理論提速，且受限于物理定律，近年單核性能提升已進入“龜速時代”。與之對比，算法優化的收益堪稱“指數級飛躍”——當數據量達到10萬時，將O(n2)復雜度優化為O(n log n)，實際運行速度可提升1000倍，這是任何硬件升級都無法實現的突破。

兼容性泥潭：不同硬件架構的指令集差異（如x86與ARM），讓硬件級優化難以通用。某金融系統曾為適配新服務器的AVX-512指令集重構代碼，結果舊型號服務器無法運行，反而引發線上故障。

數學建模：用“智慧”替代“蠻力”

真正的性能優化高手，往往通過數學模型重構解決問題。以搜索算法為例，傳統線性查詢（O(n)）在數據量增長時會變得異常緩慢。而引入跳表數據結構（本質是“空間換時間”的數學思路）后，通過建立多層索引，查詢時間直接降至O(log n)。

某社交平臺的實踐證明：在不更換任何硬件的情況下，僅通過這次數學建模優化，系統就從支持百萬級數據查詢，升級為輕松處理千萬級數據，響應速度反而提升了80%。這正是數學模型的“優越性”——它不依賴硬件迭代，而是通過優化問題的本質解法，釋放算力潛力。

與其在硬件軍備競賽中不斷投入，不如回歸代碼與算法的本質。畢竟，優秀的數學模型，才是突破性能瓶頸的“金鑰匙”。

時間復雜度的“真實面目”：平均值而非漸近線

漸近線的“理想與現實”：最壞/最好情況的局限性

在算法復雜度分析中，我們常常用漸近線來描述最壞情況和最好情況的時間復雜度，但這兩種極端場景往往難以反映算法在真實世界中的實際表現。

極端情況的局限性

以經典的快速排序（快排）為例，其最壞時間復雜度為 O(n2)，這種情況通常發生在輸入數據幾乎有序（如完全正序或逆序）時。但在隨機數據分布下，這種極端場景的發生概率極低，實際工程中幾乎可以忽略不計。與之相對的最好情況（如已排序數組且選擇中間元素作為 pivot）時間復雜度可達 O(n log n)，但這種“完美輸入”在現實業務中同樣不具普遍性——大多數數據都是隨機分布的，而非經過特殊預處理的理想狀態。

用“考試分數”理解真實性能

如果把算法性能比作學生的考試分數，漸近線分析中的最壞情況和最好情況就像是“最低分”和“最高分”。某學生某次考試最低 50 分（對應最壞情況）、最高 100 分（對應最好情況），但這兩個極端分數都無法準確反映他的真實水平。真正能代表其學習實力的，其實是多次考試后的 平均分 85 分——這就像算法的“平均情況復雜度”，更貼近實際運行時的普遍表現。

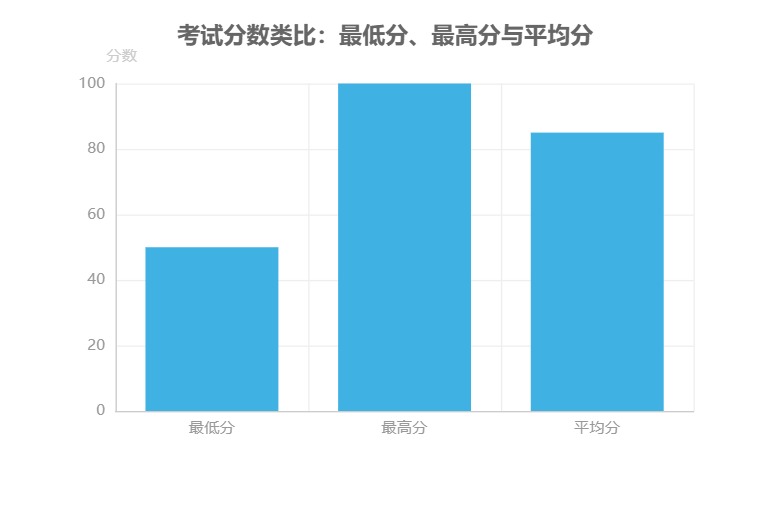
核心啟示：在評估算法性能時，僅關注最壞/最好情況就像僅憑一次考試的最高分或最低分判斷學生能力。平均情況復雜度（如快排的 O(n log n)）才是衡量算法在隨機數據下普遍表現的“真實成績單”。

通過這個類比我們能更清晰地認識到：漸近線分析提供的是理論邊界，而實際應用中需要結合數據分布特點，關注更具普遍性的平均情況復雜度，才能做出更合理的技術選型。

平均復雜度：工程中的“決策依據”

在算法設計與數據結構選型中，復雜度分析是評估性能的核心工具，但工程實踐中真正指導決策的往往不是理論上的極端情況，而是更貼近真實運行狀態的平均復雜度。以我們日常開發中頻繁使用的哈希表為例，就能清晰看到這種權衡的智慧。

哈希表的性能表現存在三種典型情況：最好情況是當哈希函數完美分配數據，無沖突發生時，插入、查找、刪除操作均可達到 O(1) 的常數級效率；最壞情況則出現在所有數據都哈希到同一位置（即哈希沖突極端嚴重）時，操作復雜度退化為 O(n)，相當于線性遍歷；而平均復雜度則是在隨機輸入下，通過合理設計哈希函數（如擾動函數、動態擴容機制）將沖突概率控制在極低水平后，實際表現出的 O(1) 效率。

這種平均復雜度主導工程決策的現象，在主流編程語言的標準庫實現中得到了充分驗證。以 Java 的 HashMap 為例，其官方文檔明確標注“平均查找時間為 O(1) ”，而非最壞情況下的 O(n)。這一細節揭示了一個關鍵事實：在大多數實際應用場景中，平均復雜度更能反映算法的真實效率，是工程師做技術選型時的核心參考。

工程啟示：平均復雜度之所以成為決策依據，本質是因為它平衡了理論嚴謹性與實際可用性。當通過技術手段（如哈希函數優化、負載因子控制、紅黑樹退化保護）將極端情況的概率降低到可接受范圍時，算法的平均表現就成為衡量其實際價值的最有效指標。

為更直觀地理解三種復雜度的適用邊界，我們可以通過表格對比其核心差異：

復雜度類型	定義場景	工程適用場景	典型應用案例
最好復雜度	理想輸入下的最優表現	理論極限分析、算法潛力評估	演示算法最優性能邊界
最壞復雜度	極端輸入下的最差表現	系統穩定性驗證、極端場景容錯設計	實時系統的最壞響應時間評估
平均復雜度	隨機輸入下的期望表現	日常開發的性能預估、數據結構選型	HashMap 查找/插入操作、數據庫索引設計

理解平均復雜度的工程意義，能幫助開發者跳出純理論的桎梏，在“完美但不實用”與“可用但有缺陷”之間找到平衡點——這正是從算法理論走向工程實踐的關鍵思維轉變。

總結與實戰建議：從“懂”到“用”的跨越

很多同學學完算法與數據結構后，常會陷入“懂原理卻做不出題”的困境——明明記得復雜度公式，實際解題時還是下意識寫出暴力解法；知道數組和鏈表的特性，卻選不對適合的存儲結構。今天我們就來拆解從“理論理解”到“實戰應用”的落地方法，用四個核心技巧+一套標準化流程，幫你把知識轉化為解題能力。

一、四個核心技巧：讓算法從“抽象”到“具體”

算法應用的本質，是用數學思維解決實際問題。這四個技巧能幫你建立“解題直覺”：

核心技巧速覽

動筆先畫再寫：寫代碼前用流程圖或偽代碼梳理邏輯，就像蓋房子先畫圖紙。比如解決“排序問題”時，先畫出冒泡和快排的步驟對比，能直觀發現快排的分治邏輯更優，避免“寫一半發現思路走不通”。
復雜度優先原則：優先選擇時間復雜度更低的算法。比如查找元素時，O(log n)的二分法比O(n)的線性遍歷效率高得多——想象在1000頁的字典里找“算法”一詞，按拼音索引（二分思路）比逐頁翻（遍歷）快20倍以上。
數據結構“對癥選藥”：根據操作場景匹配結構：頻繁增刪用鏈表（像排隊時插隊/離隊靈活，無需移動整體），隨機訪問用數組（像按座位號找人，直接定位index）；需要去重選哈希表，需要有序選紅黑樹。
數學優化是捷徑：優化先從數學模型入手，把問題“翻譯”成數學關系。比如“兩數之和”本質是“找complement=target-nums[i]是否存在”，用哈希表存儲已遍歷元素，比雙層循環更高效，這就是數學轉化的力量。

二、實戰四步走：從“拿到問題”到“寫出最優解”

面對新問題時，別急著敲代碼，按這四步走，能讓你少走90%的彎路：

實戰標準化流程

拆解問題：先明確核心需求和約束。比如“兩數之和”的核心是“找兩個數相加等于目標值”，約束是“返回索引且不能重復使用元素”。
偽代碼描述：用自然語言寫思路，比如“遍歷數組，對每個元素i，檢查數組中是否存在target - nums[i]，且索引不等于i”。
復雜度診斷：分析偽代碼的時間/空間成本。暴力解法雙層for循環是O(n2)時間復雜度（n為數組長度），空間復雜度O(1)；當n=10000時，需執行約1億次運算，會超時。
優化與實現：針對瓶頸調整。“兩數之和”的瓶頸是“重復遍歷”，用哈希表存儲已遍歷元素（key=值，value=索引），每次遍歷只需查哈希表（O(1)時間），時間復雜度降至O(n)，最后編碼實現。

三、案例演示：“兩數之和”如何從O(n2)優化到O(n)

用上面的流程，我們完整走一遍“兩數之和”的優化過程，直觀感受“從懂到用”的跨越：

問題：給定數組nums = [2,7,11,15]，target = 9，返回兩個元素的索引（答案是[0,1]）。

步驟1：拆解問題

核心需求：找兩個數之和=target，輸入是數組和target，輸出是索引數組。

步驟2：偽代碼描述

plaintext

for i from 0 to len(nums)-1:for j from i+1 to len(nums)-1:if nums[i] + nums[j] == target:return [i,j]

步驟3：復雜度診斷

時間復雜度O(n2)（兩層循環），空間復雜度O(1)。當n=10000時，運算次數達10?，遠超面試題時間限制（通常要求10?以內）。

步驟4：優化與實現

用“數學轉化+哈希表”優化：

數學轉化：將問題變為“對每個i，找complement=target-nums[i]是否存在”；
數據結構優化：用哈希表存儲已遍歷元素（key=值，value=索引），每次遍歷查哈希表（O(1)時間）；
新偽代碼：

plaintext

創建哈希表map  
for i from 0 to len(nums)-1:  complement = target - nums[i]  if complement in map:  return [map[complement], i]  map[nums[i]] = i  # 存儲當前元素和索引

此時時間復雜度O(n)（一次遍歷），空間復雜度O(n)（存儲哈希表），效率提升顯著。