一、聚類算法
概念
? ? ? ? 屬于無監督學習算法,即有特征無標簽,根據樣本之間的相似性,將樣本劃分到不同的類別中。
所謂相似性可以理解為歐氏距離、曼哈頓距離、切比雪夫距離... 。
分類
按顆粒度分為:粗聚類、細聚類。
按實現方法分為: K-means聚類、層次聚類、 DBSCAN聚類、譜聚類
二、K-Means聚類
????????K-Means 是機器學習中最經典、最常用的聚類算法之一
????????目標是在沒有先驗知識的情況下,自動發現數據集中的內在結構和模式
????????適用場景:一般大廠,項目初期在沒有 先備知識的情況下的大廠
實現流程?????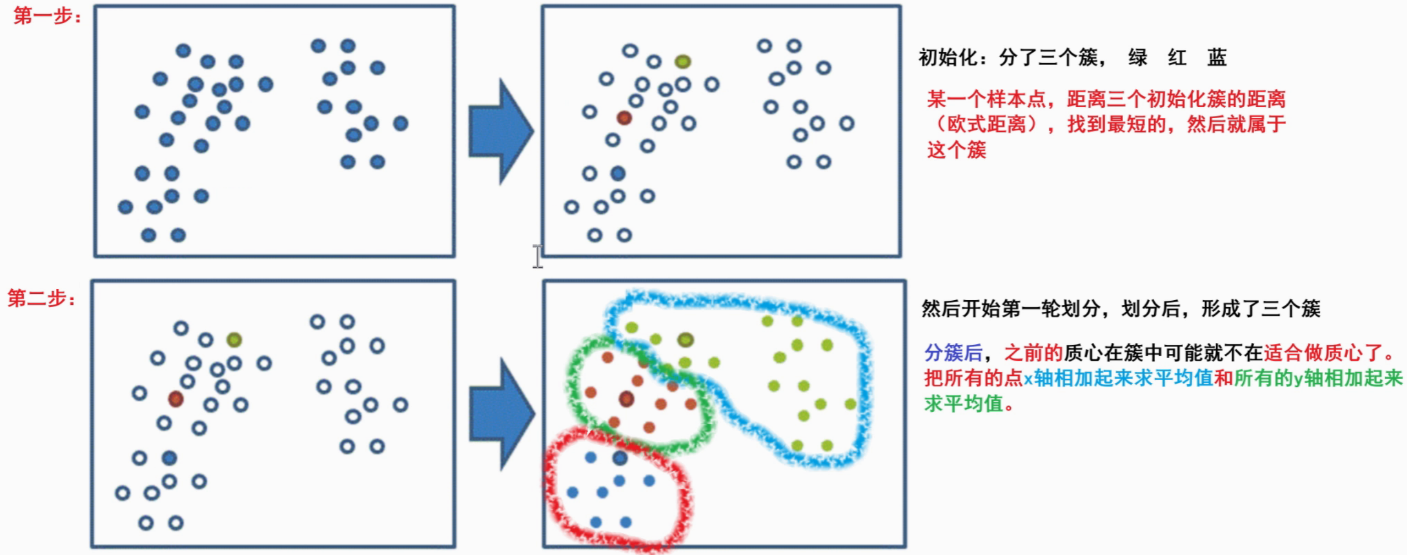

????????????????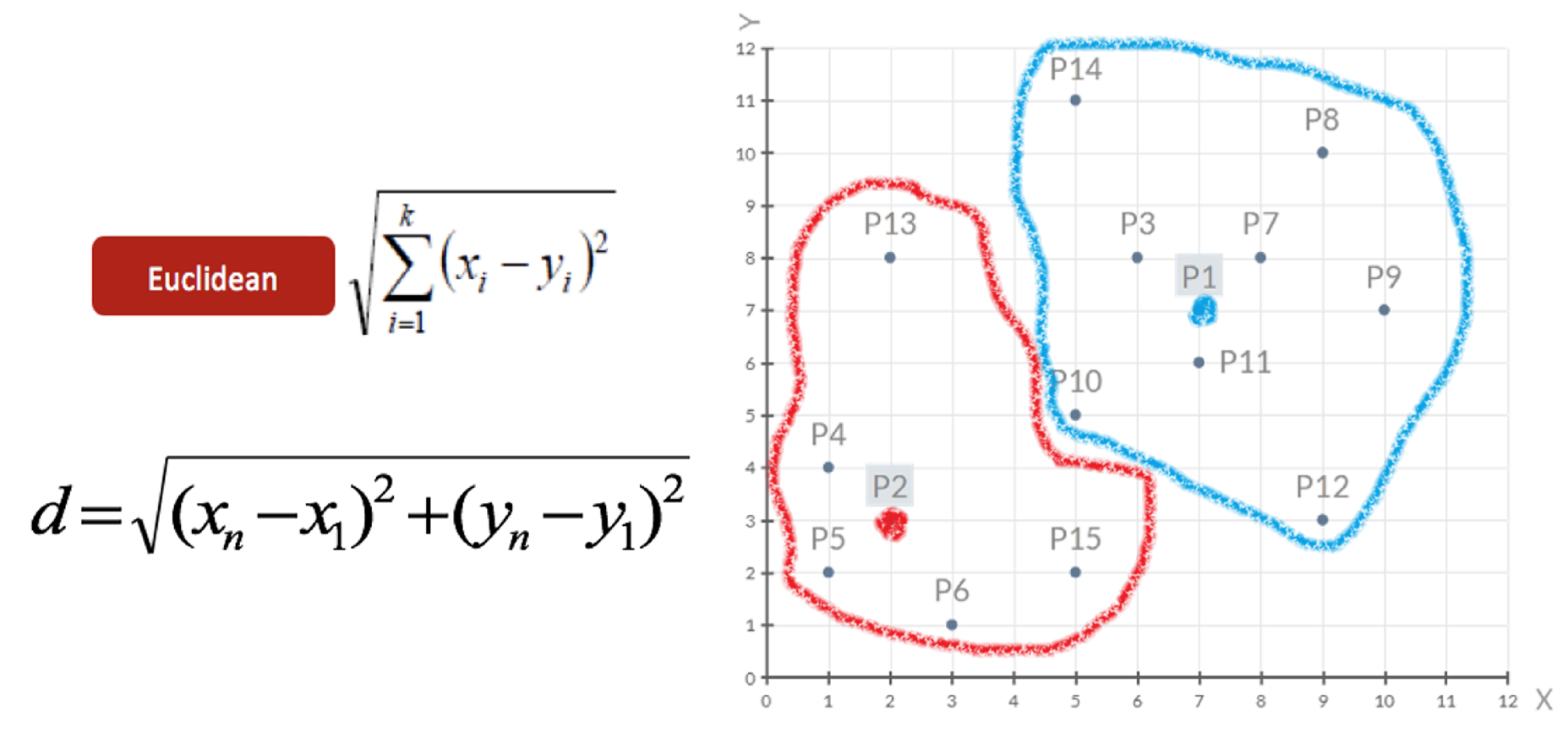
- 事先確定常數K ,常數K意味著最終的聚類類別數
- 隨機選擇 K 個樣本點作為初始聚類中心
- 計算每個樣本到 K 個中心的距離,選擇最近的聚類中心點作為標記類別
- 根據每個類別中的樣本點,重新計算出新的聚類中心點(平均值),如果計算得出的新中心點與原中心點一樣則停止聚類,否則重新進行第 3 步過程,直到聚類中心不再變化
實現API
sklearn.cluster.KMeans
# 1.導入工具包
import os
os.environ['OMP_NUM_THREADS']='4'
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs #數據生成器
from sklearn.metrics import calinski_harabasz_score # 評估指標,值越大聚類效果越好
# 2 創建數據集 1000個樣本,每個樣本2個特征,4個質心蔟,數據標準差[0.4, 0.2, 0.2, 0.2],隨機種子22
x, y = make_blobs(n_samples=1000,n_features=2,centers=[[-1,-1], [0,0], [1,1], [2,2]],cluster_std = [0.4, 0.2, 0.2, 0.2],random_state=22)
# x[:, 0]:橫坐標(第一個特征)
# x[:, 1]:縱坐標(第二個特征)
print(x) #坐標
print(y) #標簽
# 參1:橫坐標,參2:縱坐標
plt.scatter(x[:, 0], x[:, 1])
plt.show()
# 3 使用k-means進行聚類, 并使用CH方法評估
es = KMeans(n_clusters=4, random_state=22)
y_pre=es.fit_predict(x)
plt.scatter(x[:, 0], x[:, 1], c=y_pre)
plt.show()
# 4 模型評估
print(calinski_harabasz_score(x, y_pre))三、聚類算法的評估指標
1. SSE + 肘部法
SSE
- 概述:所有的簇 的所有樣本到該簇質心的 誤差的平方和
- 特點:隨著K值增加,SSE值逐漸減少
- ?目標:??SSE越小,簇內樣本越聚集,內聚程度越高
????????
肘部法—K值確定
- 對于n個點的數據集,迭代計算 k from 1 to n,每次聚類完成后計算 SSE
- SSE 是會逐漸變小的,因為每個點都是它所在的簇中心本身。
- SSE 變化過程中會出現一個拐點,下降率突然變緩時即認為是最佳 n_clusters 值。
- 在決定什么時候停止訓練時,肘形判據同樣有效,數據通常有更多的噪音,在增加分類無法帶來更多回報時,我們停止增加類別。
????????????????????????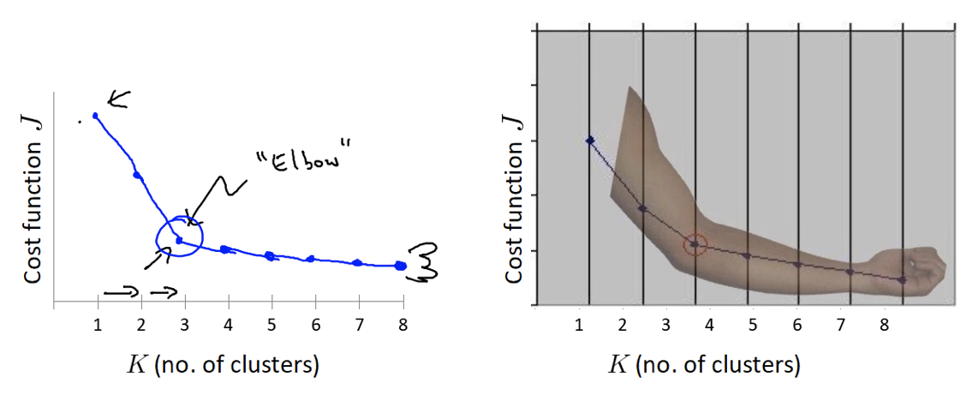
K值增大,SSE值會隨之減小,下降梯度突然變換的時候,那個K的值,就是我們要尋找得最佳值
API實現
#導包
import os
os.environ['OMP_NUM_THREADS']='4'
#導包
from sklearn.cluster import KMeans #聚類API 采用指定 質心 分簇
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs # 默認會按照高斯分布(正態分布)生成數據集 ,只需要 指定 均值 ,標準差#1、定義函數 演示:SSE+肘部法
def dm01_sse():#0、定義SSE列表 ,目的:每個K值的SSE值sse_list = []#1、獲取數據#參1:樣本數量 參2:特征數量 參3:4個簇的質點 參4:std標準差 參5:固定隨機種子x,y=make_blobs(n_samples=1000,n_features=2,centers=[[-1,-1],[0,0],[1,1],[2,2]],cluster_std=[0.4,0.2,0.2,0.2],random_state=23)#2、for訓練 訓練 獲取每個K值,對應的SSE值for k in range(1,100):#2.1創建模型#參1:簇的數量#參2:最大迭代次數#參3:固定隨機種子es=KMeans(n_clusters=k,max_iter=100,random_state=23)#2.2 訓練模型es.fit(x)#2.3獲取每個簇的sse值sse_value=es.inertia_#2.4將每個K值對應的SSE值,添加到sse_listsse_list.append(sse_value)#3.繪制SSE曲線 -》數據可視化# print(sse_list)#3.1創建畫布plt.figure(figsize=(20,10))#3.2設置標題plt.title("sse value")#3.3設置x軸plt.xticks(range(0,100,3))#參1:K值 參2:該K值所對應的SSE值# o 圓點樣式# r 紅色# - 連接數據點的樣式 實線# color='r' marker='o' linestyle='-'plt.plot(range(1,100),sse_list,'or-')plt.xlabel("k")plt.ylabel("sse")plt.grid()plt.show()if __name__ == '__main__':dm01_sse()?聚類效果評估 – 代碼效果展示SSE誤差平方和,x軸為k值,y軸為SSE值
????????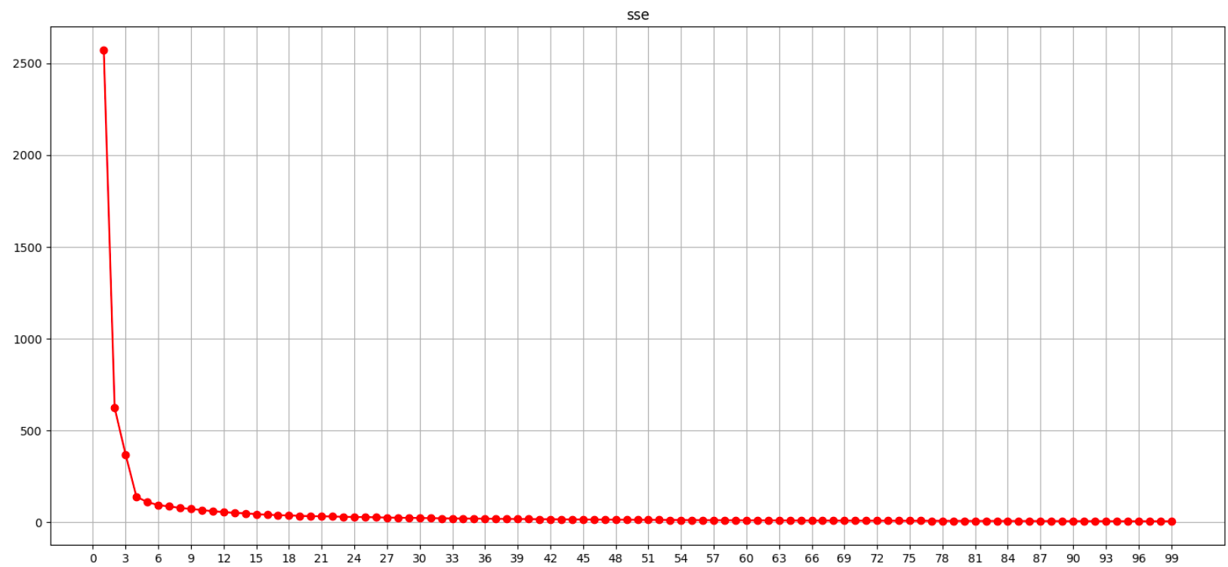
通過圖像可觀察到 n_clusters=4 sse開始下降趨緩, 最佳值4
2. SC輪廓系數法—高內聚低耦合
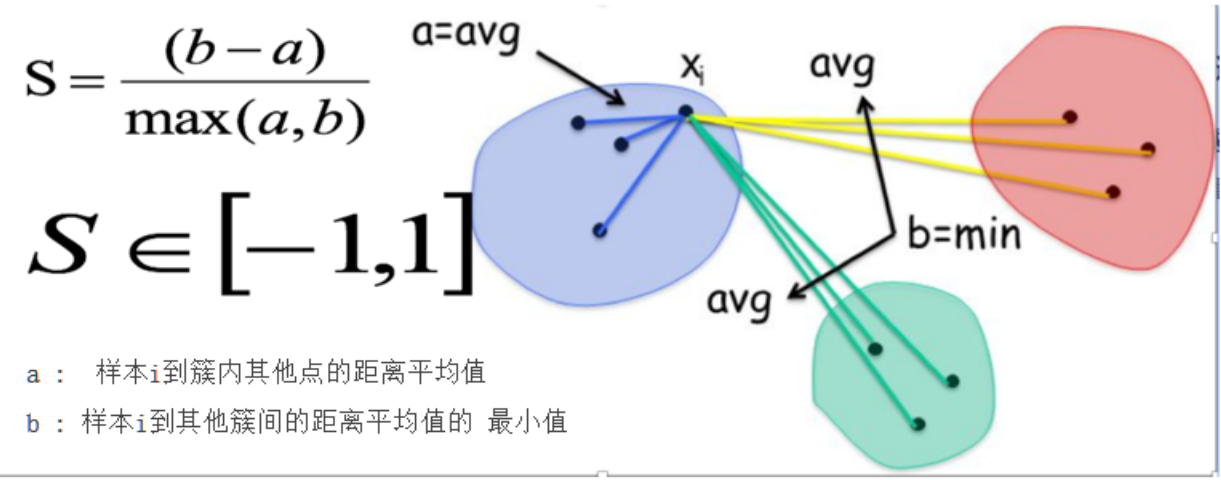
輪廓系數法考慮簇內的內聚程度(Cohesion),簇外的分離程度(Separation)
- 對計算每一個樣本 i 到同簇內其他樣本的平均距離 ai,該值越小,說明簇內的相似程度越大
- 計算每一個樣本 i 到最近簇 j 內的所有樣本的平均距離 bij,該值越大,說明該樣本越不屬于其他簇 j
- 根據下面公式計算該樣本的輪廓系數:S = b ?a/max?(a, b)
- 計算所有樣本的平均輪廓系數
- 輪廓系數的范圍為:[-1, 1],SC值越大聚類效果越好
????????????????
API實現
#導包
import os
os.environ['OMP_NUM_THREADS']='4'
#導包
from sklearn.cluster import KMeans #聚類API 采用指定 質心 分簇
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs # 默認會按照高斯分布(正態分布)生成數據集 ,只需要 指定 均值 ,標準差
from sklearn.metrics import silhouette_score,calinski_harabasz_score #silhouette_score :sc calinski_harabasz_score:chdef dm02_sc輪廓系數法():#0、定義sc列表 ,目的:每個K值的SSE值sc_list = []#1、獲取數據#參1:樣本數量 參2:特征數量 參3:4個簇的質點 參4:std標準差 參5:固定隨機種子x,y=make_blobs(n_samples=1000,n_features=2,centers=[[-1,-1],[0,0],[1,1],[2,2]],cluster_std=[0.4,0.2,0.2,0.2],random_state=23)#3、遍歷for循環 獲取每個K值 ,計算對應SC值 ,并添加到sc_list列表中for k in range(2,100): #考慮簇外 至少2簇es=KMeans(n_clusters=k,max_iter=100,random_state=23)es.fit(x)y_pre=es.predict(x)sc_value=silhouette_score(x,y_pre)sc_list.append(sc_value)#繪制sc曲線-》數據可視化plt.figure(figsize=(20,10))plt.title("sc value")plt.xticks(range(0,100,3))plt.xlabel("k")plt.ylabel("sc")plt.grid()# 注意 sc 值從2開始plt.plot(range(2,100),sc_list,'or-')plt.show()
if __name__ == '__main__':dm02_sc輪廓系數法()代碼效果展示 – SC系數
????????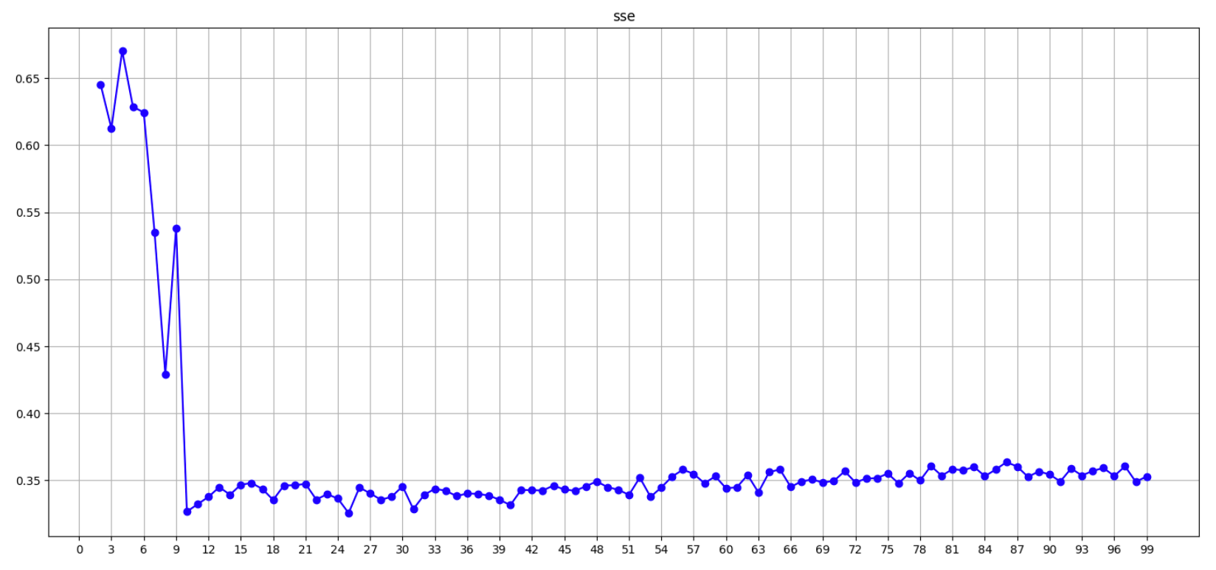
????????????????通過圖像可觀察到 n_clusters=4 取到最大值; 最佳值4
3.CH輪廓系數法—高內聚低耦合加質心
CH 系數考慮簇內的內聚程度、簇外的離散程度、質心的個數。
CH系數越大越好
- 類別內部數據的距離平方和越小越好,
- 類別之間的距離平方和越大越好,
- 聚類的種類數越少越好
????????????????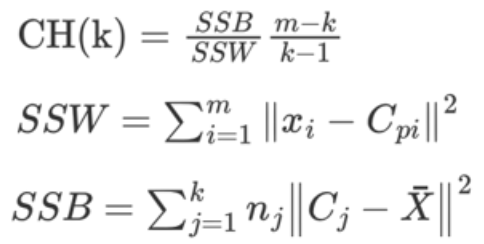

SSW 的含義:相當于SSE,簇內距離
SSB 的含義:簇間距離
API實現
#導包
import os
os.environ['OMP_NUM_THREADS']='4'
#導包
from sklearn.cluster import KMeans #聚類API 采用指定 質心 分簇
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs # 默認會按照高斯分布(正態分布)生成數據集 ,只需要 指定 均值 ,標準差
from sklearn.metrics import silhouette_score,calinski_harabasz_score #silhouette_score :sc calinski_harabasz_score:chdef dm03_CH系數():#0、定義sc列表 ,目的:每個K值的SSE值ch_list = []#1、獲取數據#參1:樣本數量 參2:特征數量 參3:4個簇的質點 參4:std標準差 參5:固定隨機種子x,y=make_blobs(n_samples=1000,n_features=2,centers=[[-1,-1],[0,0],[1,1],[2,2]],cluster_std=[0.4,0.2,0.2,0.2],random_state=23)#3、遍歷for循環 獲取每個K值 ,計算對應SC值 ,并添加到sc_list列表中for k in range(2,100): #考慮簇外 至少2簇es=KMeans(n_clusters=k,max_iter=100,random_state=23)es.fit(x)y_pre=es.predict(x)sc_value=calinski_harabasz_score(x,y_pre)ch_list.append(sc_value)#繪制sc曲線-》數據可視化plt.figure(figsize=(20,10))plt.title("ch value")plt.xticks(range(0,100,3))plt.xlabel("k")plt.ylabel("ch")plt.grid()# 注意 sc 值從2開始plt.plot(range(2,100),ch_list,'or-')plt.show()
if __name__ == '__main__':dm03_CH系數()代碼效果展示 – CH系數
????????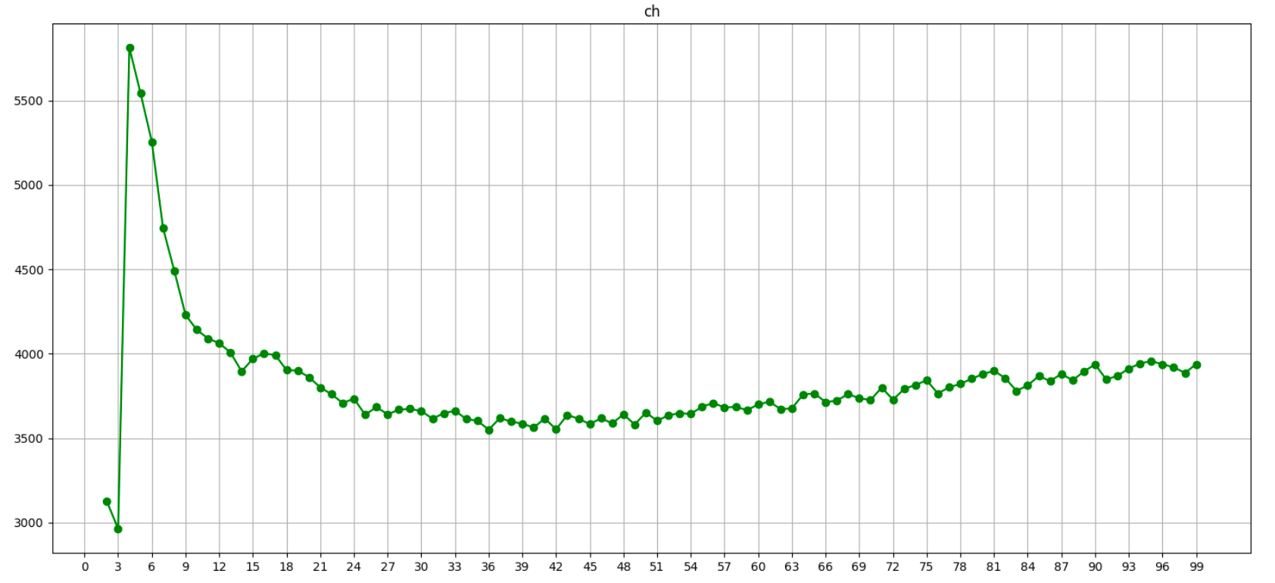
通過圖像可觀察到 n_clusters=4 取到最大值; 最佳值4




區別分析)

![[Upscayl圖像增強] docs | 前端 | Electron工具(web->app)](http://pic.xiahunao.cn/[Upscayl圖像增強] docs | 前端 | Electron工具(web->app))






核心語法課件(Node.js/React 環境))







)