電機分類

電機分類：

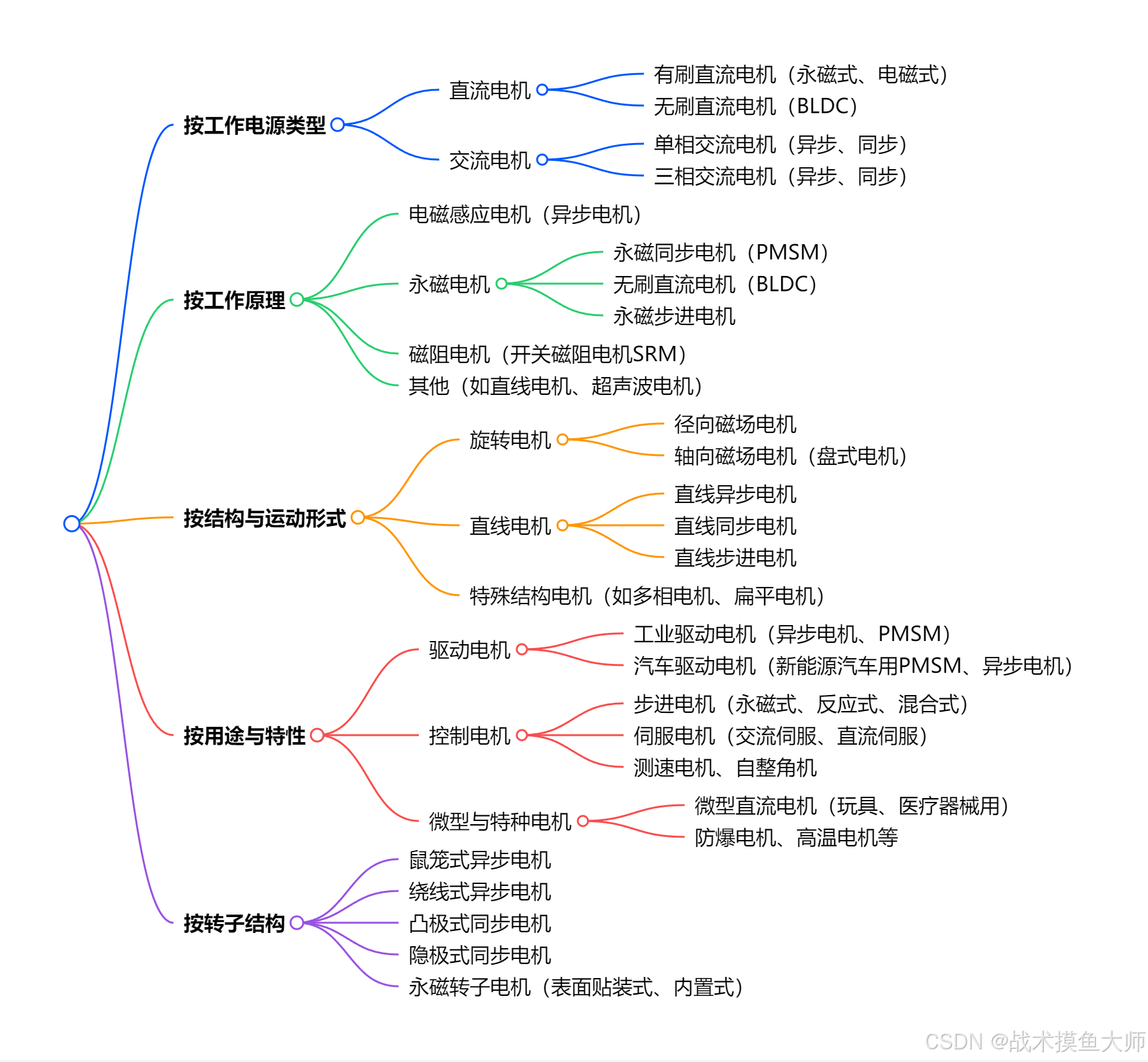
電機的拓撲模型并沒有發生太大變化,變化較大的是控制電機的方法。
常見的電機類型有：

步進電機vs伺服電機

在工業自動化、機器人、精密設備等領域，步進電機和伺服電機是兩種最常用的驅動電機，但兩者的核心原理、性能定位、控制邏輯存在本質區別，選擇時需結合精度、動態響應、成本等需求綜合判斷。下面從“核心區別”和“控制方式區別”兩方面詳細拆解：

核心區別（本質差異）

步進電機和伺服電機的根本差異源于“是否依賴反饋”——步進電機是開環控制的“位置執行器”，伺服電機是閉環控制的“高精度驅動系統”，具體可通過下表對比：

對比維度	步進電機（Stepper Motor）	伺服電機（Servo Motor）
控制邏輯基礎	開環控制（無位置/速度反饋）	閉環控制（必須搭配編碼器等反饋元件）
運動原理	按“脈沖數”轉動：每接收1個脈沖，電機轉動固定角度（如1.8°/脈沖），脈沖數決定總轉角，脈沖頻率決定轉速	按“指令目標”動態調節：通過反饋元件實時對比“指令值”與“實際值”，修正偏差，確保實際運動與指令一致
精度特性	1. 依賴“步距角精度”（如±5%），無反饋修正； 2. 存在“失步”風險（負載超過最大靜力矩時，脈沖發了但電機沒轉，且無法察覺）； 3. 低速易“丟步”，高速易“過沖”	1. 精度由“反饋元件分辨率”決定（如編碼器131072線/圈，精度遠高于步進）； 2. 閉環修正偏差，無失步風險（負載超限時會報警或降速，而非丟步）； 3. 動態精度高，低速平穩、高速無過沖
動態響應	響應慢：加速/減速需緩慢（否則易失步），無法快速跟蹤突變指令	響應快：閉環調節可快速修正偏差，能跟蹤高頻、突變的位置/速度指令（如機器人關節快速啟停）
負載能力	1. 輸出力矩隨轉速升高而下降（高速時力矩衰減明顯）； 2. 過載能力差（短期過載即失步）	1. 輸出力矩穩定（額定轉速內力矩基本不變）； 2. 過載能力強（通常可承受2~3倍額定力矩，用于短期負載峰值）
成本與復雜度	成本低：電機+驅動器結構簡單，無需反饋元件； 調試簡單（只需設置細分、電流等基礎參數）	成本高：電機+驅動器+編碼器（反饋元件），系統復雜度高； 調試復雜（需整定PID、帶寬等閉環參數）
典型應用場景	精度要求低、無動態跟蹤需求的場景： —— 3D打印機、小型數控機床（低端）； —— 流水線傳送帶、閥門控制； —— 小型自動化設備的固定位移驅動	高精度、高動態響應需求的場景： —— 工業機器人關節、高端數控機床； —— 半導體設備（晶圓搬運）、激光切割； —— 精密檢測儀器（如坐標測量機）

一般步進電機都是專用的步進電機，伺服電機是一整個伺服系統，指令 — 反饋 — 修正” 閉環，包括：伺服驅動器，電機本體，編碼器。電機一般常選用永磁同步電機PMSM（或者叫交流無刷電機）或無刷直流電機BLDC或異步感應電機IM

控制方式區別（從“開環”到“閉環”的邏輯差異）

兩者的控制方式差異直接源于“是否有反饋”，具體可拆解為“控制信號類型”“調節邏輯”“故障處理”三個層面：

1. 步進電機的控制方式（開環控制）

步進電機的控制核心是“脈沖指令直接驅動”，無需反饋，相當于“給多少脈沖，就按固定步距轉多少”，控制邏輯簡單直接。

如圖為正點原子的一款步進電機，沒有反饋單元，也沒有反饋控制。

（1）核心控制組件

• 控制器：負責輸出“脈沖信號”和“方向信號”（如PLC、單片機、運動控制卡）；
• 步進驅動器：接收控制器的脈沖/方向信號，將其轉換為電機繞組的驅動電流（如細分驅動、恒流驅動），控制電機轉動；
• 電機：無反饋元件，僅通過繞組通電順序（如兩相四拍、兩相八拍）實現步進轉動。

（2）控制邏輯流程

1. 控制器根據“目標位置”計算所需的“脈沖總數”（例：目標轉角90°，電機步距角1.8°，則需脈沖數=90/1.8=500個）；
2. 控制器按“目標轉速”輸出對應頻率的脈沖（例：轉速60rpm，步距角1.8°，則每秒脈沖數=60×360/(60×1.8)=2000Hz），同時輸出方向信號（正轉/反轉）；
3. 驅動器接收脈沖后，按“細分參數”（如16細分，將1.8°步距拆分為0.1125°/脈沖）驅動電機繞組通電，電機按固定步距轉動；
4. 無反饋環節：無論電機是否實際轉動（如負載過大導致失步），控制器都不會察覺，也不會修正——這是開環控制的最大局限。

（3）關鍵控制參數

• 細分：驅動器將電機固有步距角拆分（如16細分），用于提升精度（減小步距）和降低低速振動；
• 額定電流：根據電機參數設置驅動器輸出電流，匹配電機力矩；
• 加減速曲線：為避免啟動/停止時失步，需設置緩慢的加減速（如S型曲線），限制脈沖頻率的突變速度。

2. 伺服電機的控制方式（閉環控制）

伺服電機的控制核心是“反饋修正偏差”，相當于“先設定目標，再通過反饋實時對比實際值，修正控制量直到偏差為0”，控制邏輯更復雜但精度更高。

如圖是rm比賽中的一款常見直流無刷伺服電機6020，可以看到伺服電機不光有電機本身，還有尾部的編碼器，編碼器根據原理又分為磁編碼，光電編碼。驅動器也集成在了電機中。

（1）核心控制組件

• 控制器：輸出“位置指令”“速度指令”或“力矩指令”（如運動控制卡、PLC、伺服驅動器自帶的位置模式）；
• 伺服驅動器：核心是“閉環調節器”（通常是三環PID：位置環→速度環→電流環），接收控制器指令和編碼器反饋，計算并輸出驅動電流；
• 電機+反饋元件：電機自帶高精度編碼器（如增量式編碼器、絕對值編碼器），實時反饋電機的實際位置、速度。

（2）控制邏輯流程（以最常用的“位置模式”為例）

1. 控制器輸出“目標位置指令”（如10000個脈沖，對應編碼器的分辨率）；
2. 伺服驅動器的位置環：對比“目標位置”與編碼器反饋的“實際位置”，計算位置偏差；
3. 位置環將“位置偏差”轉換為“速度指令”，傳遞給速度環；
4. 速度環：對比“目標速度”與編碼器計算的“實際速度”（通過位置變化率得到），計算速度偏差，轉換為“電流指令”，傳遞給電流環；
5. 電流環：對比“目標電流”與電機繞組的“實際電流”，輸出PWM驅動信號，控制電機轉動，修正位置/速度偏差；
6. 實時反饋修正：編碼器每秒反饋數萬次實際位置，驅動器持續重復“對比-修正”過程，直到位置偏差接近0（通常偏差可控制在1個編碼器計數內）。

（3）關鍵控制參數與模式

• 控制模式：伺服電機支持三種核心模式，按需切換：
  • 位置模式：按位置指令（脈沖/模擬量）控制轉角；
  • 速度模式：按速度指令（模擬量/通訊）控制轉速；
  • 力矩模式：按力矩指令（模擬量/通訊）控制輸出力矩（如纏繞設備的恒張力控制）；
• PID參數整定：位置環、速度環、電流環的PID增益（比例、積分、微分）需調試，決定系統的動態響應（如響應速度、超調量）；
• 帶寬：位置環/速度環的帶寬（如位置環帶寬1kHz），決定系統能跟蹤的最高指令頻率（帶寬越高，動態響應越快）；
  • 帶寬的含義：控制帶寬通常以赫茲（Hz）為單位，表示系統增益（輸出與輸入之比）下降到低頻增益的某個特定比例（如-3 dB點）時的頻率值。在這個頻率范圍內，系統能較好地跟蹤輸入信號。
• 剛性：位置環增益的直觀體現（剛性高，位置偏差小，但易震蕩；剛性低，響應慢，但平穩）。

如何選擇？

• 若需求是“低成本、低精度、無動態跟蹤”（如固定位移、低速驅動），選步進電機（開環控制）；
• 若需求是“高精度、高動態、抗過載”（如快速啟停、實時跟蹤、精密定位），選伺服電機（閉環控制）。

簡單來說：步進電機是“按指令‘盲走’”，伺服電機是“按指令‘看著走’，走偏了就修正”——這是兩者最本質的區別。

步進電機也可以加裝編碼器，結合反饋組成伺服步進電機，可以避免大負載下的丟步現象。

直流無刷電機vs永磁同步電機vs異步無刷感應電機

直流無刷電機（BLDC）、永磁同步電機（PMSM）、異步無刷感應電機（無刷異步電機）是工業中最常用的三類無刷電機，三者的核心差異體現在磁路結構、電流波形、控制邏輯和性能特性上，適用場景也因此呈現明顯分化。以下從“核心特性”“性能參數”“應用場景”三個維度進行全面對比：

核心特性對比（結構與原理差異）

三者的本質區別源于轉子是否含永磁體及電流/反電動勢波形，這直接決定了它們的工作原理和控制方式：

特性維度	直流無刷電機（BLDC）	永磁同步電機（PMSM）	異步無刷感應電機（無刷異步電機）
轉子結構	永磁體（如釹鐵硼），表面貼裝或內置	永磁體（高性能釹鐵硼），多為內置式（提高凸極率）	無永磁體，鑄鋁鼠籠結構（靠感應電流產生磁場）
定子繞組	集中式繞組（繞組分布角度大，如120°）	分布式繞組（繞組分布角度小，如60°）	分布式繞組（與PMSM類似，但匝數和線徑適配感應特性）
反電動勢波形	梯形波（120°平頂段，三相互差120°電角度）	正弦波（平滑連續，三相互差120°電角度）	近似正弦波（由定子磁場感應產生，波形受轉差率影響）
電流波形	方波/梯形波（與反電動勢波形匹配，僅2相導通）	正弦波（與反電動勢同相位，3相同時導通）	正弦波（由逆變器輸出，需與定子磁場頻率匹配）
換向方式	電子換向（基于霍爾傳感器的“六步換相”）	電子換向（基于編碼器的“矢量控制/FOC”）	無需換向（靠定子旋轉磁場與轉子感應電流作用）
同步性	準同步（轉速≈電源頻率×60/極對數，無轉差）	嚴格同步（轉速=電源頻率×60/極對數，無轉差）	異步（轉速＜電源頻率×60/極對數，有轉差率）

關鍵性能參數對比（決定場景適配性）

性能參數的差異是三者應用場景分化的核心原因，尤其在效率、扭矩、控制精度等關鍵指標上對比顯著：

性能維度	直流無刷電機（BLDC）	永磁同步電機（PMSM）	異步無刷感應電機（無刷異步電機）
效率	中高（80%-95%，高速段效率下降明顯）	高（85%-98%，全轉速段效率平穩）	中低（75%-90%，低速段效率低，有轉子銅損）
功率密度	中（2-5 kW/kg）	高（3-8 kW/kg，永磁體貢獻高磁場密度）	低（1-3 kW/kg，需更大體積產生同等功率）
啟動/低速扭矩	較大（額定扭矩的2-3倍，梯形波電流特性）	大（額定扭矩的3-5倍，正弦波電流+高凸極率）	小（額定扭矩的1-2倍，依賴感應電流，啟動慢）
控制精度	中等（步距角精度±5%，速度波動±2%）	高（位置精度±0.01°，速度波動±0.1%）	低（速度波動±5%，無位置閉環能力）
動態響應	中（響應時間10-50 ms）	快（響應時間1-10 ms，矢量控制帶寬高）	慢（響應時間50-200 ms，轉差率導致延遲）
成本	中（永磁體成本占比20%-30%，霍爾傳感器廉價）	高（永磁體成本占比30%-50%，需高精度編碼器）	低（無永磁體，轉子結構簡單，成本比BLDC低20%）
環境適應性	中等（永磁體耐溫≤120℃，振動易導致磁性能衰減）	中等（永磁體耐溫≤150℃，高溫易退磁）	強（無永磁體，耐溫可達180℃，抗振/抗粉塵）
維護需求	低（無電刷，僅需定期檢查軸承）	中（編碼器需定期校準，永磁體需避免強磁場干擾）	低（全封閉結構，幾乎免維護）

典型應用場景對比（性能決定場景）

三者的應用場景嚴格匹配其性能特性，形成“高端精密選PMSM，中端通用選BLDC，低成本/惡劣環境選異步無刷”的格局：

應用領域	直流無刷電機（BLDC）典型場景	永磁同步電機（PMSM）典型場景	異步無刷感應電機典型場景
工業驅動	小型傳送帶、包裝機械、呼吸機泵（中速、低成本）	數控機床主軸、機械臂關節、伺服壓機（高精度、高動態）	大型風機、水泵、破碎機（低速、高負載、低成本）
汽車領域	車窗電機、座椅調節電機（低功率、低成本）	新能源汽車驅動電機、EPS轉向電機（高功率密度、高續航）	空調壓縮機、散熱風扇（高溫環境、低維護）
家電與消費電子	掃地機器人、無人機、變頻洗衣機（中等精度、低噪音）	高端變頻空調、空氣凈化器（高效率、低振動）	定頻風扇、排油煙機（低成本、簡單調速）
特種場景	醫療輸液泵、小型無人機（中等可靠性、輕量）	航空航天伺服機構、半導體設備（高精度、高穩定性）	礦山機械、冶金風機（高溫、高振動、粉塵環境）

核心區別總結與選型建議

1. 核心區別一句話概括：

   • BLDC：“梯形波驅動的永磁無刷電機”，平衡成本與性能，適合中端通用場景；
   • PMSM：“正弦波驅動的高精度永磁同步電機”，追求高性能，適合高端精密場景；
   • 異步無刷電機：“無永磁體的感應電機”，以低成本和高可靠性取勝，適合惡劣環境與簡單負載。

2. 選型優先級：

   • 若需高精度、高動態、高效率（如伺服系統、新能源汽車），選PMSM；
   • 若需中等精度、低成本、通用驅動（如家電、小型設備），選BLDC；
   • 若需耐極端環境、低維護、低成本（如礦山、冶金設備），選異步無刷電機。

三者并非替代關系，而是根據場景需求形成互補，共同覆蓋從低端到高端的無刷電機應用譜系。

電機數學模型

對于控制來說我們比較關心電機的數學模型而非物理或者結構區別。其中磁鏈方程和電氣方程是電機數學模型的兩個核心方程。
要理解電機的磁鏈方程和電氣方程，首先需要明確一個核心邏輯：電機是“電生磁、磁生電、磁受力”的能量轉換裝置，這兩個方程分別描述了“電與磁的耦合關系”和“電與磁的動態平衡關系”，是電機數學模型的基石。

磁鏈方程：描述“電流如何產生磁鏈”

磁鏈方程的本質是量化電流與磁鏈的線性耦合關系，核心是“電感矩陣”——因為電機的多個繞組（如定子三相、轉子三相、勵磁繞組等）之間既存在“自感”（自身電流產生的磁場），也存在“互感”（其他繞組電流產生的磁場）。

基礎概念

在講方程前，先明確兩個關鍵術語：

• 磁鏈（ψ，單位：韋伯·匝，Wb·t）：繞組匝數（N）與穿過繞組的磁通（Φ）的乘積，即 ψ = NΦ。它反映了繞組“鏈合”的磁場強弱，是比磁通更貼合電機分析的物理量。
• 電感（L，單位：亨利，H）：衡量電流產生磁鏈能力的參數，定義為 L = ψ / i（自感：自身電流產生的磁鏈與自身電流的比值；互感：其他繞組電流產生的磁鏈與該電流的比值，記為M）。

磁鏈方程的通用形式

電機的繞組可視為一個“電流向量”（各繞組電流的集合），磁鏈可視為“磁鏈向量”（各繞組磁鏈的集合），兩者通過電感矩陣線性關聯，通用形式為：
$$\boxed{\psi }=\boxed{L}?\boxed{i}$$

其中：

• $\boxed{\psi }=[{\psi }_1,{\psi }_2,...,{\psi }_n{]}^T$：n階磁鏈列向量（n為繞組數量，如異步電機定轉子共6個繞組，n=6）；
• $\boxed{i}=[i_1,i_2,...,i_n{]}^T$：n階電流列向量；
• $\boxed{L}$：n×n階電感矩陣，對角線元素為自感（$L_{ii}$，如定子A相自感$L_{AA}$），非對角線元素為互感（$L_{ij}$，如定子A相與B相間的互感$L_{AB}$）。

關鍵特性與示例（以異步電機為例）

異步電機是最典型的多繞組電機（定子三相繞組+轉子三相繞組，共6個繞組），其磁鏈方程能直觀體現電感矩陣的特點：

需要注意的是，三相繞組指的是輸入的電流有三相，每一相實際可以對應多個物理繞組。理論上三相只需要六個槽，實際電機中遠不止6槽，常見24槽。
可以參考這個視頻

電感矩陣的結構

異步電機的電感矩陣 ${\boxed{L}}_{6\times 6}$ 可按“定子繞組”和“轉子繞組”分塊，形式如下：
$$\boxed{L}=\left[\begin{array}{cc}{\boxed{L}}_s& {\boxed{L}}_{sr}\\ {\boxed{L}}_{rs}& {\boxed{L}}_r\end{array}\right]$$

• ${\boxed{L}}_s$（3×3）：定子繞組自互感矩陣，對角線為定子各相自感（$L_{ss}$，三相對稱時相等），非對角線為定子相間互感（$L_{sm}$，如$L_{AB}=L_{BC}=L_{CA}=?L_{sm}$，負號因繞組空間相差120°，磁鏈方向相反）；
• ${\boxed{L}}_r$（3×3）：轉子繞組自互感矩陣，結構與${\boxed{L}}_s$對稱（轉子三相也對稱）；
• ${\boxed{L}}_{sr}$（3×3）、${\boxed{L}}_{rs}$（3×3）：定轉子互感矩陣，滿足${\boxed{L}}_{sr}={\boxed{L}}_{rs}^T$（互感可逆），且隨轉子位置變化（因為轉子旋轉會改變定轉子繞組的空間相對位置，導致互感時變，這是異步電機方程“耦合、時變”的核心原因）。

異步電機磁鏈方程的展開

以定子A相（${\psi }_A$）和轉子a相（${\psi }_a$）為例，展開后可直觀看到電流對磁鏈的貢獻：

• 定子A相磁鏈：${\psi }_A=L_{ss}{i}_A+L_{sm}{i}_B+L_{sm}{i}_C+M_{sr}\cos \theta i_a+M_{sr}\cos (\theta +120°)i_b+M_{sr}\cos (\theta ?120°)i_c$
  （前三項是定子電流產生的磁鏈，后三項是轉子電流產生的磁鏈，$\theta$為定轉子空間夾角）；
• 轉子a相磁鏈：${\psi }_a=M_{sr}\cos \theta i_A+M_{sr}\cos (\theta ?120°)i_B+M_{sr}\cos (\theta +120°)i_C+L_{rr}{i}_a+L_{rm}{i}_b+L_{rm}{i}_c$
  （前三項是定子電流產生的磁鏈，后三項是轉子電流產生的磁鏈）。

實際應用中的關鍵簡化

原始磁鏈方程因“時變互感”（如異步電機的$\theta$變化）和“多繞組耦合”，求解復雜，工程中常用坐標變換（如dq0變換、αβ變換）簡化：

• 變換后，定轉子繞組的“時變互感”變為“恒定互感”，“三相耦合”變為“dq軸解耦”；
• 簡化后的磁鏈方程（如dq軸下）：${\psi }_d=L_d{i}_d$，${\psi }_q=L_q{i}_q$（同步電機），或${\psi }_s=L_s{i}_s+L_m{i}_r$，${\psi }_r=L_m{i}_s+L_r{i}_r$（異步電機矢量控制模型），大幅降低控制難度。

在電機控制中需要用到矢量變換，對于三相電機，主要有三個坐標系
坐標系統：三相靜止（abc）坐標，兩相靜止（αβ）坐標、兩相旋轉（dq0）坐標
變換方法：Clarke 變換、Park 變換是 “從原始坐標系到目標坐標系的數學工具”。
Clarke 變換實現 “三相靜止→兩相靜止（αβ）”，Park 變換實現 “兩相靜止（αβ）→兩相旋轉（dq）”，兩者結合可完成 “三相靜止（abc）→兩相旋轉（dq0）” 的完整變換。
這部分后續還會再提到。

影響磁鏈方程的核心因素

• 氣隙長度：氣隙越大，磁阻越大，自感和互感越小（電感與磁阻成反比）；
• 鐵芯飽和：上述方程默認“線性電感”（鐵芯不飽和），實際中鐵芯飽和會導致電感隨電流增大而減小，需引入“非線性電感模型”修正；
• 繞組結構：繞組匝數越多、導線越粗，自感越大；繞組空間夾角越小，互感越大。

電氣方程：描述“電壓與磁鏈、電流的動態平衡”

電氣方程的本質是基爾霍夫電壓定律（KVL）在電機繞組中的延伸，核心是“電壓 = 電阻壓降 + 感應電動勢”——但電機的感應電動勢分為兩類，需特別注意。

核心物理量：兩類感應電動勢

電機繞組中的感應電動勢并非只有“變壓器電動勢”，還有“運動電動勢”，兩者的區別是理解電氣方程的關鍵：

• 變壓器電動勢（$e_t=?\frac{d\psi }{dt}$）：磁鏈隨時間變化產生的電動勢（如變壓器副邊感應電動勢），與繞組是否旋轉無關，僅由$\psi$的變化率決定，符號由楞次定律（阻礙磁鏈變化）確定；
• 運動電動勢（$e_v=\omega \times \psi$）：繞組在磁場中旋轉（或磁場相對繞組運動），導體切割磁感線產生的電動勢（如發電機的感應電動勢），與“磁鏈大小”和“旋轉角速度（ω）”成正比，方向由右手定則確定。

在電機繞組中，感應電動勢的產生本質是導體切割磁感線或磁通量穿過繞組發生變化（法拉第電磁感應定律），但根據磁場來源和繞組運動關系的不同，核心可分為旋轉電動勢（動生電動勢） 和變壓器電動勢（感生電動勢） 兩類。
旋轉電動勢的核心是繞組導體與磁場發生相對運動，導體切割磁感線產生的電動勢，因常見于轉子繞組旋轉切割定子磁場的場景（如直流電機、異步電機轉子），故得名 “旋轉電動勢”；從電磁感應本質看，屬于法拉第定律中的 “動生電動勢”（由導體運動導致磁通量變化）。
變壓器電動勢的核心是繞組導體靜止，但穿過繞組的磁通量隨時間變化（如交變磁場），導致繞組中產生的電動勢，因與變壓器原副邊繞組的感應機制完全一致，故得名 “變壓器電動勢”；從電磁感應本質看，屬于法拉第定律中的 “感生電動勢”（由磁場變化導致磁通量變化，與導體運動無關）。

電氣方程的通用形式

對于任意一個電機繞組，其端電壓（u）滿足：
$$u=Ri+e_t+e_v$$

代入兩類電動勢的表達式，展開為：
$$u=Ri+\frac{d\psi }{dt}+\omega \times \psi$$

（注：若繞組靜止，如定子繞組，運動電動勢$e_v=0$，方程簡化為$u=Ri+\frac{d\psi }{dt}$；若磁鏈恒定，如直流電機穩態，變壓器電動勢$e_t=0$，方程簡化為$u=Ri+e_v$）。

關鍵示例（以同步電機dq軸為例）

同步電機的轉子有勵磁繞組，且以同步角速度（ω?）旋轉，工程中常用“dq0坐標變換”將三相繞組等效為“d軸（直軸，與勵磁磁場同向）”和“q軸（交軸，與勵磁磁場垂直）”的兩相繞組，其電氣方程最具代表性：

電機中存在兩個主要磁場：勵磁磁場、電樞磁場。其中勵磁磁場為主磁場，建立 “穩定的、用于能量轉換的基礎磁場”。電樞磁場與勵磁磁場相互作用，產生電磁轉矩（電動機）或感應電動勢（發電機）。
電機運行過程中，電樞磁場會對勵磁磁場（主磁場）產生影響，這種影響稱為電樞反應，為了抵消電樞反應的負面影響，電機設計中會采取專門措施：如直流電機在定子上增加 “補償繞組”（抵消電樞磁場），同步電機在轉子上設置 “阻尼繞組”（抑制磁場畸變）。

d軸電氣方程（定子d軸繞組）

$$u_d=R_s{i}_d+\frac{d{\psi }_d}{dt}?{\omega }_1{\psi }_q$$

• $u_d$：定子d軸端電壓；$R_s$：定子電阻；$i_d$：d軸電流；${\psi }_d$：d軸磁鏈；
• 關鍵項：$?{\omega }_1{\psi }_q$是d軸的運動電動勢（因q軸磁鏈在d軸繞組中旋轉產生，負號由dq軸正交關系決定）。

q軸電氣方程（定子q軸繞組）

$$u_q=R_s{i}_q+\frac{d{\psi }_q}{dt}+{\omega }_1{\psi }_d$$

• 關鍵項：$+{\omega }_1{\psi }_d$是q軸的運動電動勢（d軸磁鏈在q軸繞組中旋轉產生，方向與d軸相反）。

勵磁繞組電氣方程（轉子勵磁繞組，靜止于d軸）

$$u_f=R_f{i}_f+\frac{d{\psi }_f}{dt}$$

• 勵磁繞組隨轉子旋轉，但始終與d軸同向，無運動電動勢（$e_v=0$）；
• ${\psi }_f=L_f{i}_f+L_{fd}{i}_d$（勵磁磁鏈由勵磁電流$i_f$和定子d軸電流$i_d$共同產生，$L_f$為勵磁自感，$L_{fd}$為定轉子d軸互感）。

電氣方程與磁鏈方程的關聯

電氣方程中的$\psi$（磁鏈）需通過磁鏈方程計算（$\psi =Li$），因此兩個方程是“嵌套關系”：

1. 由電流$\boxed{i}$通過磁鏈方程得到$\boxed{\psi }$；
2. 將$\boxed{\psi }$代入電氣方程，得到電壓$\boxed{u}$與電流$\boxed{i}$的動態關系。

這種關聯是電機“電壓-電流-磁鏈”動態特性的完整描述，也是電機仿真（如MATLAB/Simulink）和控制系統設計（如矢量控制、直接轉矩控制）的核心依據。

兩個方程的核心應用場景

理解磁鏈方程和電氣方程，本質是掌握電機的“數學語言”，其應用貫穿電機分析與控制的全流程：

1. 電機運行狀態分析：如異步電機啟動時的電流沖擊（磁鏈方程中互感時變導致$\frac{d\psi }{dt}$增大，電氣方程中電壓不變則電流增大）；
2. 控制系統設計：如矢量控制的核心是“通過坐標變換，將時變的磁鏈/電氣方程轉化為解耦的直流電機模型”，實現對磁鏈和轉矩的獨立控制；
3. 故障診斷：如電機繞組短路時，自感減小，磁鏈方程中$\psi$與$i$的比值異常，可通過電氣方程的電壓電流偏差診斷故障。

總結

對比維度	磁鏈方程	電氣方程
核心物理關系	電流 → 磁鏈（磁耦合）	電壓 → 電流 + 磁鏈（能量平衡）
關鍵參數	自感、互感（電感矩陣）	電阻、磁鏈變化率、旋轉角速度
核心電動勢	無（僅描述磁鏈產生）	變壓器電動勢 + 運動電動勢
工程簡化手段	坐標變換（解耦時變互感）	結合磁鏈方程，將$\psi$替換為$Li$
本質作用	建立“電→磁”的定量關系	建立“電→磁→電”的動態平衡

簡言之：磁鏈方程是“因”（電流產生磁鏈），電氣方程是“果”（磁鏈變化產生電動勢，與電壓平衡），兩者共同構成了電機能量轉換的數學核心。