一、前情提要
有個Java數據轉換的小示例:
public class Example2_2 {public static void main(String[] args) {float f = 123456.6789f;System.out.printf("f=%30.12f", f);}
}
輸出的結果是:
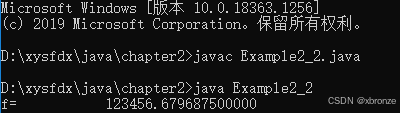
123456.679687500000
這里就發現了個問題,我變量f定義的值是123456.6789,為什么輸出的結果小數位變了呢??
簡單來說,核心原因是 float類型的精度有限,無法精確表示123456.6789
Java 中float是32 位單精度浮點數,遵循 IEEE 754 標準。它的存儲結構由 1 位符號位、8 位指數位和 23 位尾數位(實際有效精度約 24 位)組成。
這種結構導致float只能精確表示有限的十進制小數,對于大多數十進制小數(如代碼中的123456.6789),它無法精確存儲,只能存儲一個最接近的近似值。
那么如何理解float類型無法精確表示123456.6789??
要理解“float類型無法精確表示123456.6789”,需要從計算機如何存儲小數說起。這本質上是“二進制與十進制的轉換限制”和“float的存儲空間有限”共同導致的問題,我們一步步拆解:
二、計算機如何存儲小數以及float空間限制
1. 計算機只認識二進制,不認識十進制
我們日常用的是十進制(0-9),但計算機內部所有數據(包括小數)都必須轉換成二進制(0和1)存儲。
對于整數(如123),十進制轉二進制是“除2取余”,結果是有限的二進制數(比如123的二進制是1111011),可以精確存儲。
但小數的轉換要復雜得多:十進制小數轉二進制的方法是“乘2取整”,例如0.6789轉二進制的過程是:
- 0.6789 × 2 = 1.3578 → 取整數部分1(二進制小數第一位是1)
- 剩下的0.3578 × 2 = 0.7156 → 取整數部分0(第二位是0)
- 剩下的0.7156 × 2 = 1.4312 → 取整數部分1(第三位是1)
- 剩下的0.4312 × 2 = 0.8624 → 取整數部分0(第四位是0)
- … 以此類推
這個過程可能無限進行下去(永遠無法得到整數1.0),就像十進制中1/3=0.3333…無限循環一樣。
也就是說:大部分十進制小數無法用有限長度的二進制精確表示,只能得到一個近似值。
2. float類型的“存儲空間”被嚴格限制
Java的float是32位單精度浮點數,遵循IEEE 754標準,它的存儲空間被分成3部分:
- 1位符號位(表示正負)
- 8位指數位(表示數值的大小范圍)
- 23位尾數位(表示數值的精度,即有效數字)
關鍵限制在這里:尾數位只有23位(加上默認的1位隱藏位,總共24位有效精度)。
24位二進制能表示的有效數字相當于多少位十進制呢?
通過公式換算:24 × log??(2) ≈ 7.2位。
也就是說:float最多只能精確表示6-7位十進制有效數字,超過這個范圍的數字會被“舍入”,導致精度丟失。
3. 為什么123456.6789無法被float精確表示?
我們來看123456.6789的有效數字:
整數部分是123456(6位),小數部分是6789(4位),總共是10位有效數字(1-2-3-4-5-6-6-7-8-9)。
而float最多只能精確到7位有效數字,第8位及以后的數字無法精確存儲,只能根據二進制轉換規則進行“四舍五入”。
具體來說:
當你寫float f = 123456.6789f時,計算機需要把123456.6789轉換成二進制,但因為:
- 小數部分0.6789的二進制是無限循環的
- 尾數位只有23位,無法容納全部二進制 digits
最終計算機只能存儲一個“最接近123456.6789的二進制近似值”。當這個二進制近似值再轉換回十進制時,就變成了123456.6796875(而不是原來的123456.6789)。
4. 一個更簡單的類比
假設你有一個只能寫7個數字的筆記本,現在要記錄“123456789”(9個數字)。
因為本子空間不夠,你只能記一個近似值,比如“123456800”(前7位保留,后面的四舍五入)。
float的問題和這個類比完全一樣:它的“筆記本”(尾數位)只能放下相當于7位十進制的有效數字,對于123456.6789(10位有效數字),只能記錄一個近似值。
三、總結
float無法精確表示123456.6789的核心原因是:
- 十進制小數轉二進制時,大部分是無限循環的,無法用有限位數表示;
- float的尾數位只有23位(約7位十進制精度),無法容納123456.6789的10位有效數字,只能存儲近似值。
這也是為什么輸出結果是123456.6796875——這是float能存儲的最接近原始值的近似值。


)














)
)
