目錄

1.程序功能描述

2.測試軟件版本以及運行結果展示

3.部分程序

4.算法理論概述

5.完整程序

---

1.程序功能描述

? ? ? ?在壓印過程中，一般情況下，我們遵循質量，動量和能量守恒的原則進行仿真。然后建立偏微分方程組，然后通過有限元的方法，將方程離散化，然后進行求解，得到最后的結果。

2.測試軟件版本以及運行結果展示

MATLAB2022A/MATLAB2024B版本運行

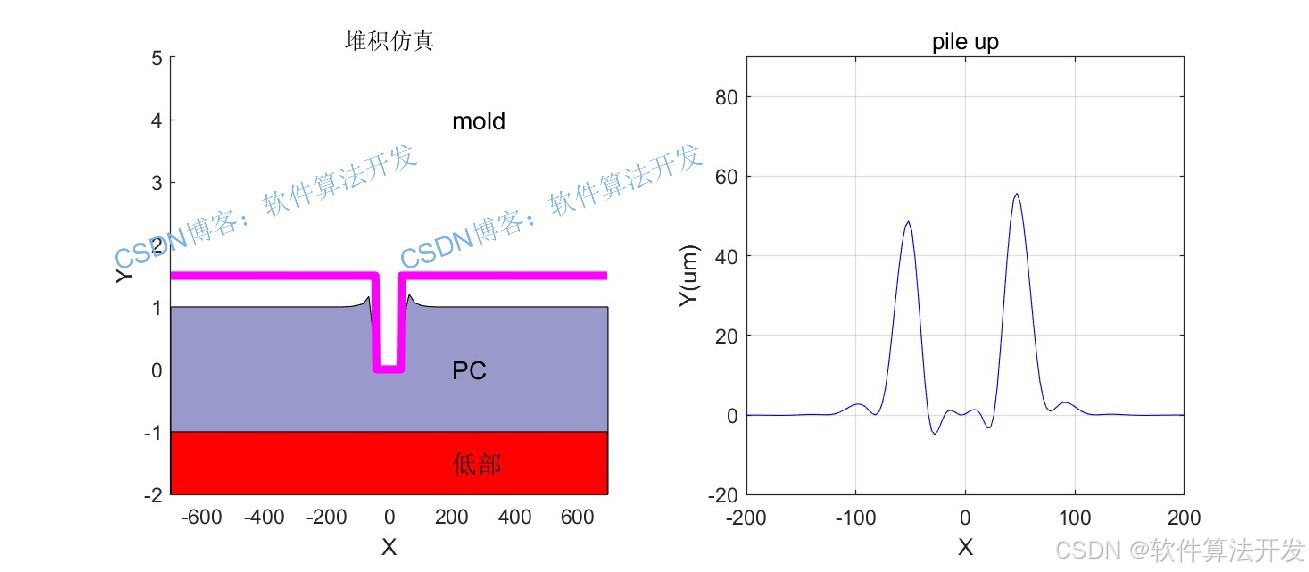
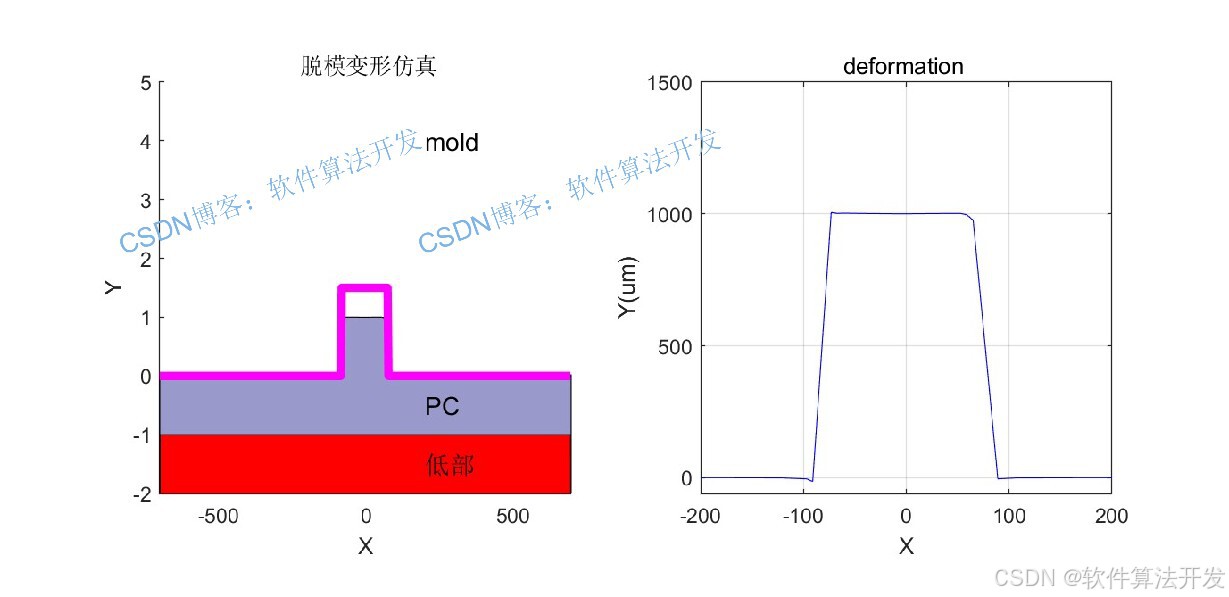
3.部分程序

%參數初始化
Mold_Move_Set    = [0:5:75];
latitude         = 100000;
Fliud_Thick_Thin = 10;
delrho           = 2;
Width_Pitch      = 50;
Scale            = 50;
Alphas           = 999;
H                = Fliud_Thick_Thin;
g                = 9.8;
delr             = delrho/1000.;      
c                = sqrt(delr*g*H);  
Ks               = 8.64e4;
%主函數
f                = func_glasswave(latitude);
%變形半徑
Radius_dem       = c/abs(f+1e-20);        
W                = Width_Pitch/Radius_dem;
Scale2           = abs(Scale);
[coffg1,coffg2]  = func_coff(g,delr,Scale2,f,Radius_dem,H,c);
Mach             = coffg2/c;
dx               = 3e3;
Lmax             = 700e3;       
Lmin             = 500e3;     
x_array          =-Lmax:dx:Lmax;   
Len_x_array      = length(x_array);
N1               = round((Lmax - Lmin)/dx);
N2               = Len_x_array - round((Lmax - Lmin)/dx);
Ldindex          = func_wind(Len_x_array,N1,N2);
Decays           = (1./(Alphas*Ks));  
%偏微分方程的有限元分割步進
FEM_Step         = 0.1;              
dt               = FEM_Step*dx/c;             
Nsteps           = round(0.2*Ks/dt);
%數值仿真分割數 
K                = 40;
Kd               = sqrt(K*0.2*Ks)/1000;
NonLinear1       = 1;      
NonLinear2       = 1;      
[m,nu]           = size(x_array);
xh               = ones(1,nu-1);
xh               = cumsum(xh)*dx;
nh               = nu - 1;.................................
034_001m1

4.算法理論概述

第一種結構如下所示：

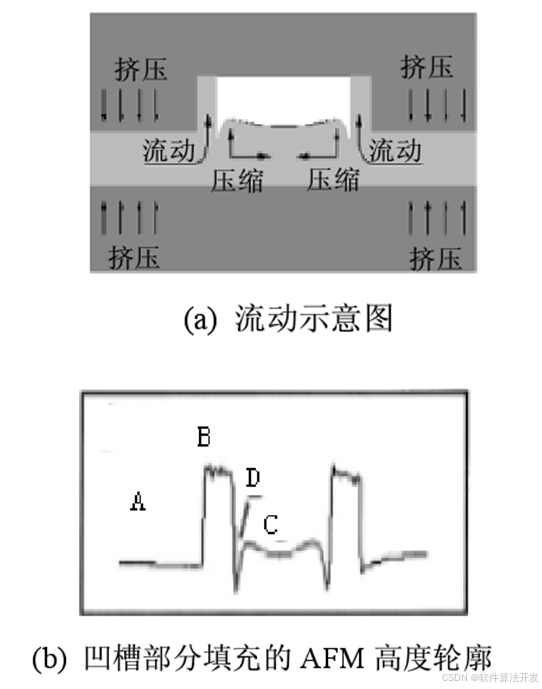
? ? ? ?即聚合物的橫向（從周邊）粘性流動。對于圖(a)的只有一個凹槽結構的簡單模板壓印情形，模板凸區下的聚合物受到強烈擠壓而流入相鄰兩個凸區之間的空腔中，并沿著空腔側壁上升，而空腔內原有的聚合物由于受到兩側流體的擠壓，會向上凸起變形，兩股流體不能融合為一體，因而在交界處形成凹性接點。隨著壓印時間的延長，兩側聚合物不斷向空腔內擠壓，原有的聚合物不斷壓縮上升，最后整個空腔被填滿。

第二種結構如下所示：

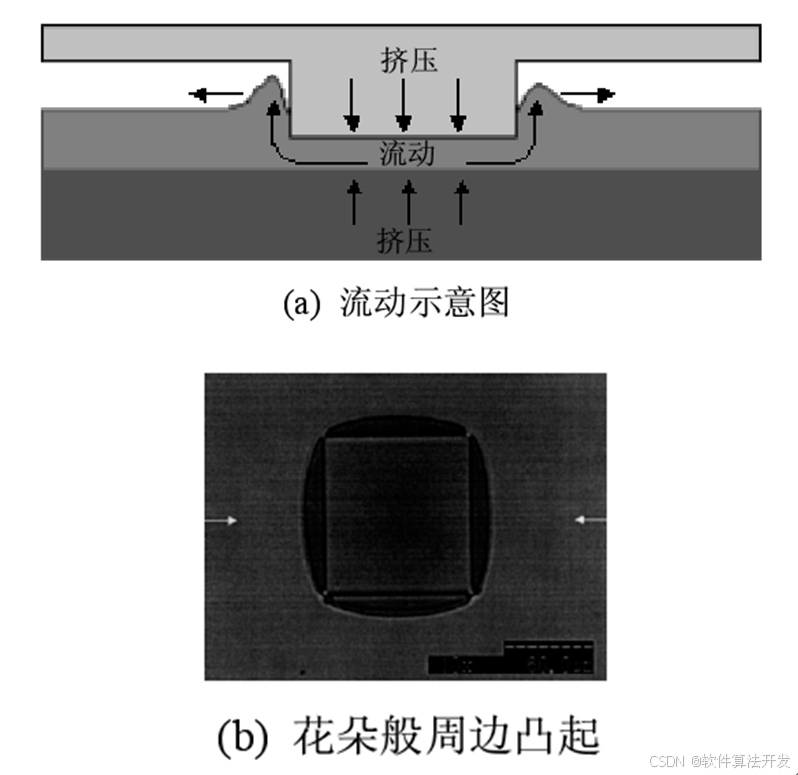
?????? 對于圖 (a)只有一個凸起結構的模板壓印情形，凸模下方的聚合物受到壓擠而向周邊流動，由于被擠出的聚合物與周邊聚合物相比，數量較少，難以順暢推動周邊聚合物，因而在兩股流體的匯合處形成類型花朵的突起。

????? 納米壓印開始時，聚合物流動一般表現為橫向粘性流動，如果聚合物薄膜各處力學性能或溫差或壓力等存在較大差異，尤其是當聚合物膜較薄和壓力又較大時，聚合物便會從薄膜表面上隆起。

????? 隆起密度和高度與聚合物薄膜性能的一致性程度和具體壓印條件有關。隆起產生后，與聚合物的橫向粘性流動交替作用，使得填充壓模空腔中的聚合物不斷從橫向和縱向兩個方向擴展直至充滿整個空腔。

????? 上述納米壓印聚合物的流動機理對于優化壓印工藝條件和模板設計具有重要意義。當模板尺寸較小，且凸區和凹區結構尺寸相近時，聚合物一般以簡單流動機理填充空腔，容易充分填滿空腔；當凹區結構尺寸與凸區相比相對較大，尤其是空腔的深寬比又較大時，聚合物轉移相對困難，易產生縱向隆起，需要較大的壓力或較高的壓印溫度或較厚的聚合物薄膜；當模板尺寸較大時，且凸區和凹區結構尺寸相近的圖形結構，如果能保持各處的壓力和溫度的一致性，聚合物也較容易充分轉移；但如果模板周邊具有大量的空白區域，尤其是當空腔深寬比又較大時，由于聚合物的流動主要來自周邊，各空腔填空次序不一，越靠近中心的空腔越不易填充，此時需要較大的壓力或較高的壓印溫度或較大壓印深度。

?????? 上述的過程，簡單的講，就是這么兩個過程：

向凹入的間隙中填沖；

被突出的模板擠向兩邊；

????? 然后，我們的模型，就是上述過程的周期性運動：

????? 上述兩種情況，在本質上，其數學模型是類似的，這里進行詳細的介紹和說明：

????? 在宏觀領域，基于任意的拉格朗日—歐拉方法(ALE)的流體動力學方程被用來處理復雜的流固耦合過程。一般在固體力學中，習慣采用Lagrange坐標系；而流體力學中更多地使用Euler坐標系。這樣可以使計算網格不再確定，也不依附于流體質點，而可以相對于坐標架做任意運動，以實現網格的不斷更新而不致發生畸變。

建模的時候，遵循質量，動量，能量守恒原則。

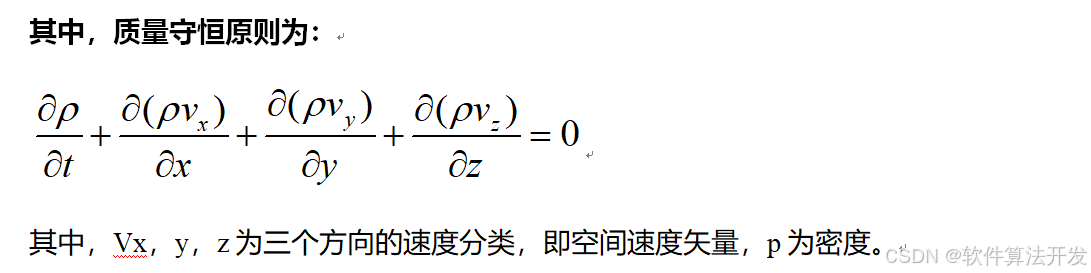
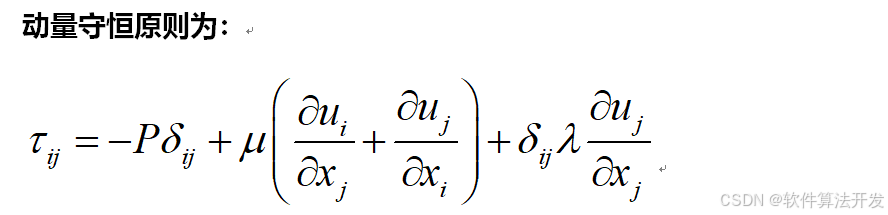
5.完整程序

VVV