【線性代數基礎 | 那忘算9】基爾霍夫（拉普拉斯）矩陣矩陣

~~之前學的不扎實導致現在還得回來再學。~~

專欄指路：《再來一遍一定記住的算法（那些你可能忘記了的算法）》

前置知識：

生成樹：在一個無向連通圖中，能夠連接所有頂點的樹結構。

點的度數：與這個點相連的邊有多少條。

矩陣及矩陣乘法定義。

沒學過行列式的建議看我寫的這個

（注意行列式這個非常重要！！一定要會！）

秩：矩陣的線性無關的行向量數量，高斯消元后有幾個非零行，秩就是幾。

前導：

求出一個無向連通圖的生成樹并不難，但如果我們想求出圖的所有生成樹數量呢？

（如果你還不知道怎么求生成樹，也許可以看看我的這篇最小生成樹）

1.基爾霍夫矩陣

基爾霍夫矩陣（Kirchhoff matrix），由德國物理學家古斯塔夫·基爾霍夫發明。

后因定義與數學中的拉普拉斯矩陣高度重合，所以兩者在中文語境里是相同的。

（后文中出現的拉普拉斯矩陣都指基爾霍夫矩陣）

定義：當 $i=j$ 時， $L[i][j]$ 為 $i$ ?點的度數。

當 $i!=j$ 時，如果兩點有邊相連， $L[i][j]$ 為?節點 i 和 j 之間邊數的負值

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? （但因為重邊一般會特判，直接等于 $-1$ ?也可以），反之為 $0$ 。

也寫作? $L=D-A$ ? 。

其中? $L$ ?是拉普拉斯矩陣， $D$ ?是度矩陣（只有 $D[i][i]$ ?不為 $0$ ， $D[i][i]$ ?= 點 $i$ ?的度數）。

$A$ ?是鄰接矩陣（?當 $i=j$ ?時為? $0$ ?;

? ? ? ? ? ? ? ? ? ? ? ? ? ?其他時候，如果兩點有邊相連， $A[i][j]$ ?為 $1$ ，反之為 $0$ ）。

通常教程會告訴你：

啊，矩陣樹定理就是給無向連通圖建個基爾霍夫矩陣，去掉某一行某一列，

再求個行列式，就是這個圖的生成樹數量啦！

道理都懂，但是生成樹數量為什么會和行列式掛鉤啊！！

2.拉普拉斯矩陣和關聯矩陣

要想探究上面那個問題，我們要引入一個新的概念——

關聯矩陣：稱? $B$ ?是一個 $n*m$ ?矩陣，其中 $B[i][j]=1$ ?如果頂點 i 是邊 j 的一個端點，

如果? $B[i][j]=-1$ ?頂點 i 是邊 j 的另一個端點（對每條邊任意指定方向），否則 $B[i][j]=0$ 。

對于拉普拉斯矩陣? $L$ ，我們有：

$L=B*B^T$

等等，這個? $B^T$ ?是啥？

它是矩陣轉置（Transpose）是指將矩陣的行和列互換的操作。

對于一個矩陣 $B$ ，其轉置記為? $B^T$ （也寫作 $B'$ ）。

這么表示： $B^T[i][j]=B[j][i]$

比如說這個矩陣：

$\begin{vmatrix} 1 & 2 & 3 &4 \\ 8 & 7 & 6 & 5 \end{vmatrix}$

它的轉置就是：

$\begin{vmatrix} 1 & 8\\ 2 & 7\\ 3 & 6\\ 4 & 5 \end{vmatrix}$

再說回這個式子：

$L=B*B^T$

分類討論 $B*B^T$ ?矩陣的每個元素：

對角元素? $(i = i)$ ：

$(B*B^T)[i][i]=\sum_{k=1}^{m}B[i][k]*B^T[k][i]=\sum_{k=1}^{n}B[i][k]^2$

= 頂點 i 的度數（因為每條與 i 相連的邊貢獻 $(\pm 1)^2$ ）

非對角元素? $(i \neq j)$ ：

$(B*B^T)[i][j]=\sum_{k=1}^{m}B[i][k]*B^T[k][j]=\sum_{k=1}^{n}B[i][k]*B[j][k]$

如果 i 和 j 之間有一條邊，則該項為 -1（因為 $B[i][k]$ ?和? $B[j][k]$ ?符號相反）；

如果 i 和 j 之間沒有邊，則為 0。

這正好就是拉普拉斯矩陣? $L$ ?的定義！

3.柯西—比內公式（Cauchy–Binet formula）及其應用

知道了這個? $L=B*B^T$ ?有啥用呢？

我們還得上點科技——柯西—比內公式。

公式具體長這個樣子：

設 $A$ ?是 $m*n$ ?矩陣， $B$ ?是 $n*m$ ?矩陣，其中 $m\leq n$ ，則有：

$det(AB)=\sum_{S}^{}det(A_s)*det(B_s)$

其中求和是對所有從 $\left \{ 1,2,...,n \right \}$ ?中選取 $m$ ?個元素的子集 $S$ ?進行的，

$A_S$ ?表示 $A$ ?中選取 $S$ ?對應的列組成的 $m*m$ ?子矩陣，

$B_S$ ?表示 $B$ ?中選取 $S$ ?對應的行組成的 $m*m$ ?子矩陣。

我寫的不嚴謹證明在這里，不建議看證明，直接背公式就行。

3.5.線性相關

在代入公式之前，我們還要對矩陣做處理。

設? $L[i]$ ?為拉普拉斯矩陣去掉第 i 行第 i 列得到的 $(n-1)*(n-1)$ ?矩陣。

$B[i]$ ?為關聯矩陣去掉第 i 行得到的 $(n-1)*m$ ?矩陣。

為什么要這么做？首先我們知道生成樹的邊一定是? $n-1$ ?條。

但這不算最重要的原因，最重要的是最開始是拉普拉斯矩陣是線性相關的！

線性相關的官方定義：在線性代數里，矢量空間的一組元素中，

若沒有矢量用有限個其他矢量的線性組合所表示，則稱為線性無關或線性獨立。

反之則稱為線性相關。

啊其實就是你用其他的元素一通計算搗鼓，能整出這個元素，那就是線性相關。

在矩陣中，把矩陣的每一行都看作一個? $n$ ?維向量，

如果有一行和其他行向量加減/放縮的結果相等，

即這個矩陣線性相關。

而在拉普拉斯/關聯矩陣里，如果有幾行向量加起來是 0 向量，

那么這個矩陣就是線性相關，行列式為 0。

但是線性相關的矩陣行列式為什么為 0 ？

我們把矩陣的每一行都看作一個? $n$ ?維向量，

而行列式就是這? $n$ ?個向量張成的面積。

如果有兩個向量線性相關，也就是一個是另一個的倍數，

那張出的面積肯定為 0。

（同學們可以自己試一下二階和三階矩陣，意會即可）

很明顯，拉普拉斯矩陣的每一行都加起來得到的向量是為 0 的。

比如說圖? $1-2-3$ ，它的拉普拉斯矩陣長這樣：

$\begin{vmatrix} 1 & -1 & 0\\ -1 & 2 & -1\\ 0& -1 & 1 \end{vmatrix}$

每一列都單獨加起來，得到? $(0,0,0)$ 。

設? $r_i$ ?為第 i 行的向量表示，那么我們就有：

$r_1+r_2+r_3=0$

$r_1+r_2=-r_3$

也就是? $r_3$ ?能被別的向量通過計算表示，線性相關。

這是一個很重要的點，我們知道方程組中的一個方程如果能被其他方程表示，

那么這個方程就是“沒用”的，也就是整個矩陣的秩為? $n-1$ 。

更直接的，線性相關的矩陣的行列式都為 0！

因為有一行（一個方程）是“沒用”的，相當于那一行都為 0。

而有一行都為 0 的矩陣的行列式為 0！

也就是原來的拉普拉斯矩陣是“沒用”的！

為了讓它變得有用，我們考慮去掉它的一行或者一列。

但不能只丟掉一行或者一列，因為柯西—比內公式要求最終乘積結果只能是方陣。

（而且你只求掉一行或者一列的話，那方程組不就多解或者無解了嗎？！）

所以就把一列和一行同時丟掉。

再來說關聯矩陣為什么要去掉一行。

在拉普拉斯矩陣已經變成? $(n-1)*(n-1)$ ?的情況下，

當然是要去掉一行的了。

（不然最后乘出來是 $n*n$ ?的矩陣）

還有個原因，關聯矩陣也是線性相關的！

不去掉行列式為 0，根本沒法算。

（我服了怎么回事你倆）

話又說回來：

把這個? $L[i]=B[i]*B[i]^T$ ?代入公式：

$det(AB)=\sum_{S}^{}det(A_s)*det(B_s)$

$det(L[i])$

$=det(B[i]*(B[i])^T)$

$=\sum_{S\subseteq E,|S|=n-1}^{}det(B[i]_s)*det(B[i]^T_s)$

$=\sum_{S\subseteq E,|S|=n-1}^{}det(B[i]_s)^2$

其中求和是對所有從邊集? $E$ ?中選取 $n-1$ ?條邊的子集 $S$ ?進行的，

$B[i]_S$ ?表示 $B[i]$ ?中選取 $S$ ?對應的列組成的 $(n-1)*(n-1)$ ?子矩陣，

$B[i]^T_S$ ?表示 $B[i]^T$ ?中選取 $S$ ?對應的行組成的 $(n-1)*(n-1)$ ?子矩陣。

（因為 $B_S$ ?是選對應的列，也就是邊，所以子集 $S$ ?也是選邊）

4.生成樹與行列式的關系

有了這玩意，才算真正邁上正軌：

$det(L[i])=\sum_{S\subseteq E,|S|=n-1}^{}det(B[i]_s)^2$

考慮選出來的? $n-1$ ?條邊構成的圖。

我們發現要不就是這樣：

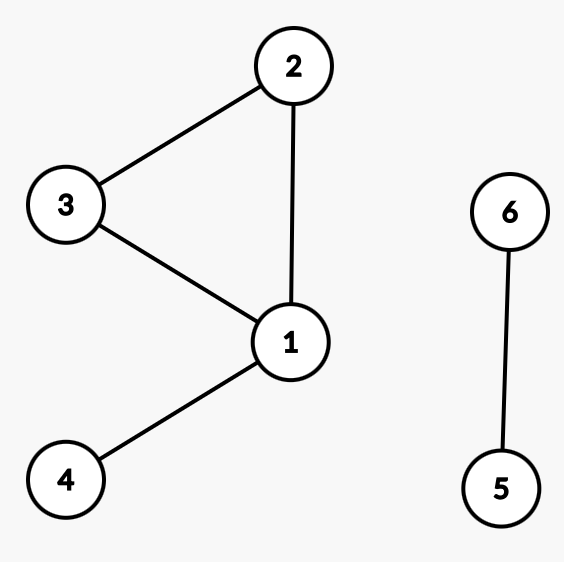（有環不連通）

要不就是這樣：

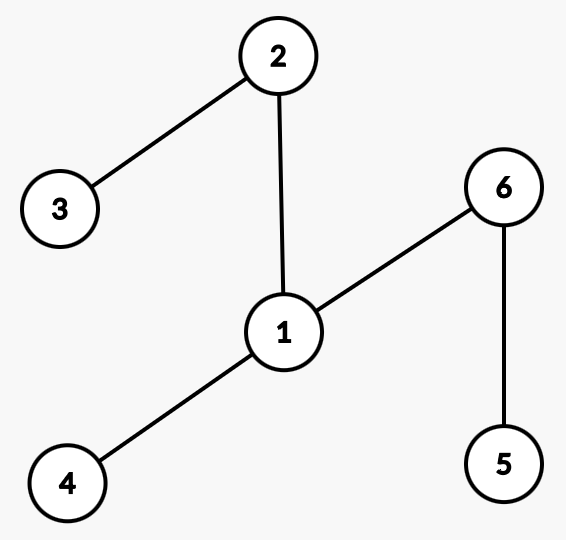（無環聯通/生成樹）

同學們可以自己畫一下，是不可能出現無環不連通的情況的。

因為你每加一條不成環的邊，都會增加一個點，而邊數 = 點數 - 1。

同樣的，有環連通也不可能出現。

分類討論下：

（1）有環不連通

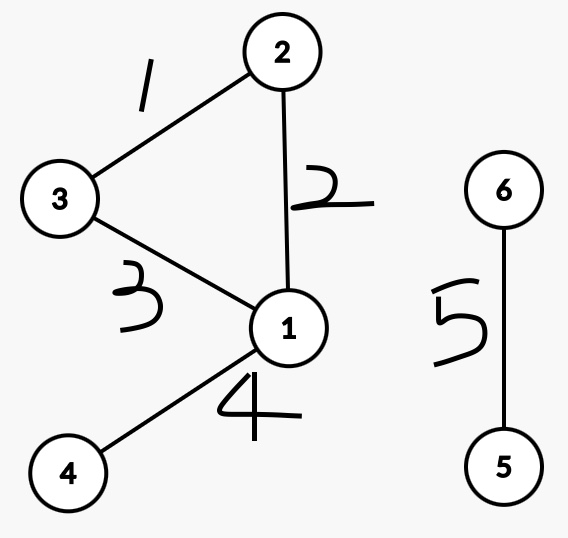根據上面這張圖，構造關聯矩陣。

（關于邊的方向，我就默認從小連到大，這個不影響）

$B=\begin{vmatrix} 0 & 1 & 1 & 1 &0 \\ 1 & -1 & 0 & 0 & 0\\ -1 & 0 & -1 & 0 & 0\\ 0 & 0 & 0 & -1 & 0\\ 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & -1 \end{vmatrix}$

去掉最后一行：

$B[6]=\begin{vmatrix} 0 & 1 & 1 & 1 &0 \\ 1 & -1 & 0 & 0 & 0\\ -1 & 0 & -1 & 0 & 0\\ 0 & 0 & 0 & -1 & 0\\ 0 & 0 & 0 & 0 & 1\end{vmatrix}$

很明顯，這個矩陣是線性相關（上面 4 行加起來是 0 向量）的，行列式為 0。

$det(L[i])=\sum_{S\subseteq E,|S|=n-1}^{}det(B[i]_s)^2$

上面這公式統計的時候，遇到這種有環不連通的圖，

行列式都為 0，相當于啥也沒發生。

一般性的想一下，如果去掉的一行（點）不在環上。

那環所在的連通塊的行（點）一定線性相關。

（環連通塊的邊連的倆點一個 +1 一個 -1，加起來肯定是 0）

如果去掉的一行（點）在環上，但肯定還有其他連通塊。

畢竟一個環要和點數一樣的邊數，要點數 = 邊數 + 1，肯定還有別的連通塊沒環。

那其他連通塊的行（點）一定線性相關。

（和之前理由相同，其實只要有一小塊是在去掉點之前就連通的，

? ?并且也沒被去掉點，那么那小塊的行加起來肯定是 0 向量）

（2）無環連通/生成樹

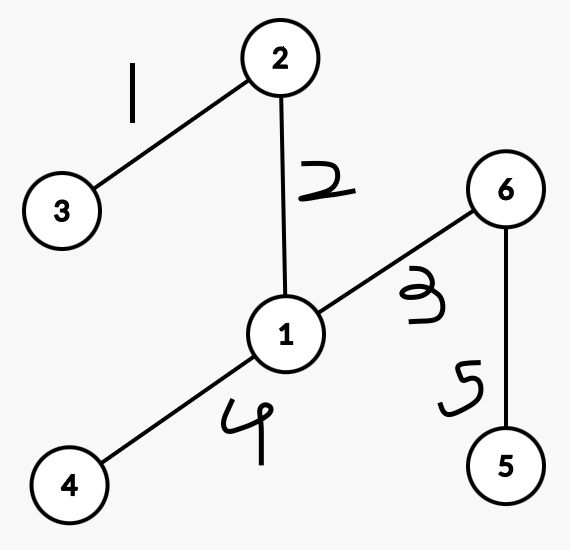根據上面這張圖，構造關聯矩陣。

$B=\begin{vmatrix} 0 & 1 & 1 & 1 &0 \\ 1 & -1 & 0 & 0 & 0\\ -1 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & -1 & 0\\ 0 & 0 & 0 & 0 & 1\\ 0 & 0 & -1 & 0 & -1 \end{vmatrix}$

我們發現，無論去掉哪行，都不可能線性相關。

（雖然去掉一個點，圖里還是會有連通塊。

? ?但我們去掉的是點，不是邊，消失的邊對另一點的影響還在。

? ?多出來的影響會導致最終加起來的行向量，對應消失的邊的那一維不可能為 0）

$det(L[i])=\sum_{S\subseteq E,|S|=n-1}^{}det(B[i]_s)^2$

所以在這個求和式里，選出的? $n-1$ ?條邊只有在無環連通/生成樹的情況下，

行列式才不為 0，可以被統計到。

這就是為什么：

啊，矩陣樹定理就是給無向連通圖建個基爾霍夫矩陣，去掉某一行某一列，

再求個行列式，就是這個圖的生成樹數量啦！

既然學完了，那就再看看矩陣樹定理的官方定義吧：

矩陣—樹定理（matrix-tree theorem）：

圖的生成樹數目等于其基爾霍夫矩陣的任一代數余子式行列式值。

更準確地說，對于一個 n 個點 m 條邊的無向圖，

其生成樹總數為其對應的基爾霍夫矩陣的 n-1 階余子式（行列式）。

5.代碼實現

沒學過高斯消元指路這里。

全套基爾霍夫矩陣行列式求生成樹數量的代碼：

#include<bits/stdc++.h>
using namespace std;typedef long long LL;
const int N = 110;
LL K[N][N], ans;
int n, m; void add(int x, int y) {K[x][x]++; K[y][y]++;K[x][y]--; K[y][x]--;
}void gauss() {n--;  // 去掉一行，現在處理(n-1)×(n-1)子矩陣int r = 1; ans = 1;for (int c = 1; c <= n; c++) {for (int i = r + 1; i <= n; i++) {while (K[i][c]) { LL bs = K[r][c] / K[i][c]; for (int j = 1; j <= n; j++) {K[r][j] -= K[i][j] * bs;}swap(K[r], K[i]); ans *= -1; }}if (K[r][c] != 0) {r++;}}// 檢查是否滿秩（圖是否連通）if (r <= n) {cout << 0 << "\n";  // 非連通圖，生成樹數量為0return;}for (int i = 1; i <= n; i++) {ans *= K[i][i];}cout << abs(ans) << "\n";  // 取絕對值確保非負
}int main() {cin >> n >> m;memset(K, 0, sizeof(K));for (int i = 1; i <= m; i++) {int x, y;cin >> x >> y;if (x != y) {  // 忽略自環（不影響生成樹）add(x, y);}}gauss();return 0;
}