LC11 盛最多水的容器
選擇兩條線，它們與x軸構成的容器可以盛的水量取決于兩條線中較短的那條以及兩條線之間的距離。

樸素的思想是使用i和j遍歷height中的所有線，但是這樣的時間復雜度是$O(n^2)$。

我們讓i從0開始，j從n-1開始，組成一個容器。

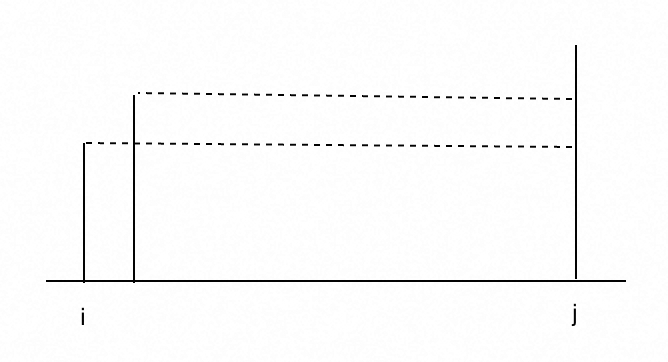
不妨假設height[0]<=height[n-1]，則固定左端點組成的所有容器中，無論右端點在哪，容器的盛水高度不可能高過左端點的線高，故初始容器就是固定左端點組成的所有容器中盛水量最多的容器。這里本質上把固定左端點對右端點進行$O(n)$的掃描通過分析變成了$O(1)$。

i=0的情況看完了，接下來應該移動左端點i。這里本質上是在固定右端點對左端點進行掃描。我們將左端點移動到比初始線高更高的第一個位置，則組成容器的盛水高度會變高，才有可能盛水量更多。則容器左端點從初始的i=0到現在位置中的所有左端點，其右端點一直保持j=n-1，因為不需要掃描，對于這些左端點，移動右端點不會使得盛水量更多。這里的分析就是算法的時間復雜度下降的原因。我們只需要分析如何讓容器向著盛水量可能變大的方向去變化，每次移動較矮側的端點至下一個更高位置處即可。

最終容器的變化過程就是，每次讓容器較矮的一側變的更高，直到兩個端點重合。這樣時間復雜度就是左右端點共同掃描完原數組，即$O(n)$。

這里我們對完備性進行一些簡單證明。我們算法移動左右端點的過程中不會固定某一個端點對另一個端點進行$O(n)$的掃描都是因為通過分析可知，當我們在移動一側的過程中，沒有移動的那一側無論取在哪也不會使得盛水量變大，所以盛水量最多的情形只要其左端點或者右端點作為過我們算法移動過程中的對應左端點或右端點，則我們的算法一定會得到不小于盛水量最多情形的結果。而由于那又是盛水量最多的情形，所以不小于即為等于。

class Solution {public int maxArea(int[] height) {int left=0,right=height.length-1,ans=0;while(left<right){ans=Math.max(ans,Math.min(height[left],height[right])*(right-left));if(height[left]<=height[right]){int std=height[left];//讓left向右移動到一個更高的位置for(;left<right;left++){if(height[left]>std) break;}}else{int std=height[right];//讓right向左移動到一個更高的位置for(;right>left;right--){if(height[right]>std) break;}}}return ans;}
}

這里的i和j就是雙指針，從兩側向中間收攏，每次變化都向著可能使得盛水量變大的方向變化，且每次變化的特點是容器的盛水高度更高，寬度更小。這一題的變化過程分析對LC42 接雨水的解題有幫助。

LC42 接雨水
這道題也可以一樣使用從兩側向中間收攏的雙指針。我們下圖中的線實際是一個寬度為1的柱子，這里畫圖簡化了。

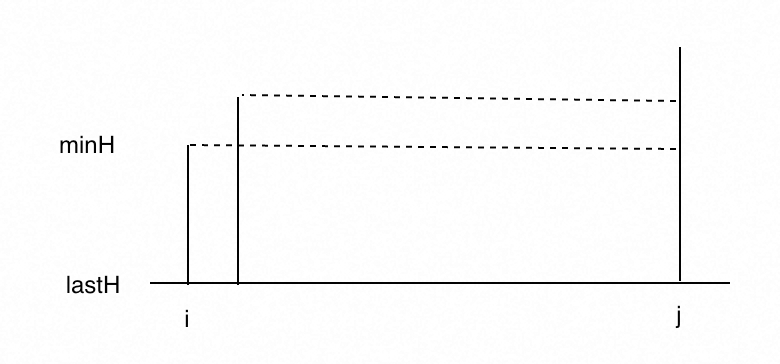
我們記minH為當前兩個端點柱子高度的較小值，一開始讓i=0，j=n-1，lastH為地面高度為0。則初始狀態可以計算出lastH到minH高度之間的雨水量。

不妨假設height[0]<=height[n-1]，則無論怎么移動右端點，i=0高于minH的部分都不會有雨水，這點和LC11中的容器很像。所以對于i=0的部分，不需要花費$O(n)$去遍歷右端點j，這時應該直接移動左端點i至下一個更高的柱子處，找到積水高度更高的“容器”。找到后，更新minH的值，并將原本minH的值給lastH，計算雨水量的增量是新的minH和最初minH即當前lastH之間的雨水，且容易反證在當前左端點左側高于初始minH的部分不可能有雨水，這點和LC11中的容器也很像，因為該部分不屬于新容器的范圍。

這樣我們一樣是以$O(n)$的時間復雜度遍歷了所有可能有雨水的左右端點情形，以樸素的思想，會在每個我們更新更高柱子的“容器”中遍歷中間的每個寬度計算當前i到j寬度之間、當前lastH到minH高度之間的雨水量，這樣總時間復雜度是$O(n^2)$，不是最優。

接下來需要再利用一定的分析技巧去降低時間復雜度，我們不要在每次“容器”改變形狀時去遍歷寬度計算雨水。我們有如下發現，以我們的左端點來看，我們會讓左端點i從0變化到下一個更高柱子處，然后繼續到下一個更高的柱子處，所有的雨水不會出現在每一個更高的柱子處，只會出現在我們移動左端點前后的中間的柱子處，且雨水高度也均為移動前的minH。所以我們有更聰明的計算雨水的方法，每次移動端點時，計算該端點處的雨水量（minH-height[i]，以左端點為例），而不再每次去遍歷寬度計算“容器”內的lastH到minH高度之間的雨水量。這樣總時間復雜度就被優化至$O(n)$。

class Solution {public int trap(int[] height) {int n=height.length,i=0,j=n-1;int minH,ans=0;while(i<j){minH=Math.min(height[i],height[j]);//i和j處較矮者向中間移動，移動至更高處停止//每次移動，計算移動的那個寬度的雨水量if(height[i]<=height[j]){for(;i<j&&height[i]<=minH;i++){ans+=minH-height[i];}}else{for(;i<j&&height[j]<=minH;j--){ans+=minH-height[j];}}}return ans;}
}