機器學習--PCA降維

一·核心部分? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?

1解決的問題：應對高維數據帶來的計算量大、冗余信息多、易出現過擬合等問題，在減少數據維度的同時盡可能保留原始數據的關鍵信息。

2核心思想：從高維數據中提取少數幾個主成分，這些主成分是原始特征的線性組合，能最大程度保留數據方差（信息）且相互正交（無關聯），以此實現降維。

3關鍵概念：包括主成分（原始特征的線性組合，用于替代高維特征）、方差（衡量數據信息多少的指標，主成分需最大化方差）、正交性（主成分之間互不相關，避免信息重復）。

二·原理加推導

數學概念

（1）內積：

A與B的內積：A?B=∣A∣∣B∣cos(α)

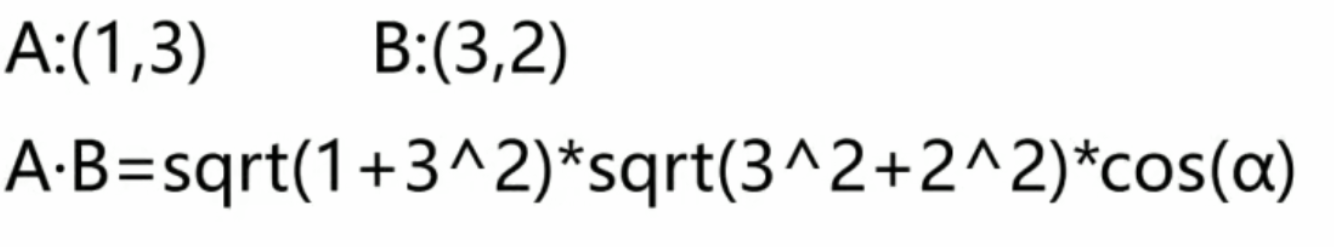
sqrt就是根號

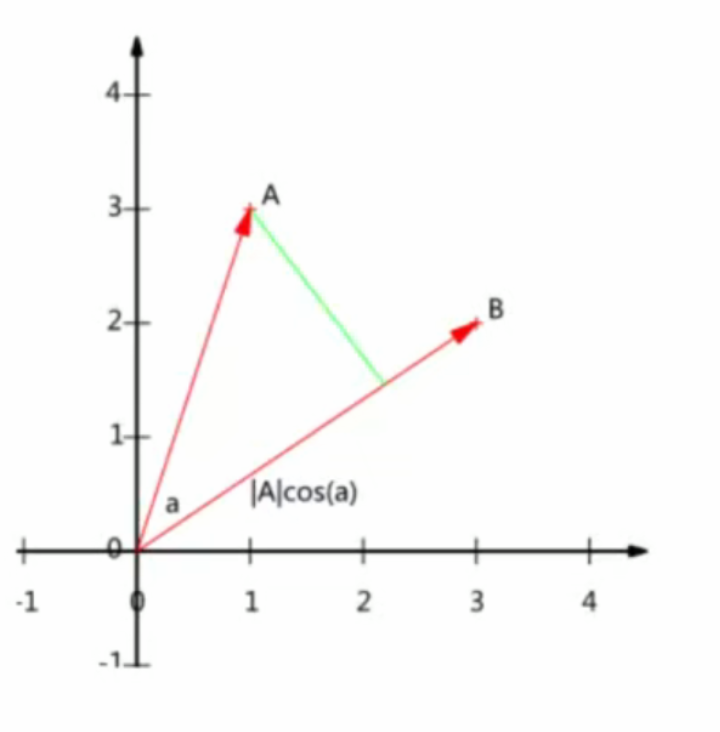
假設向量B的模等于1，即(|B| = 1)，此時A到B的投影變成了：(A ·?B = |A| cos(α))

（2）

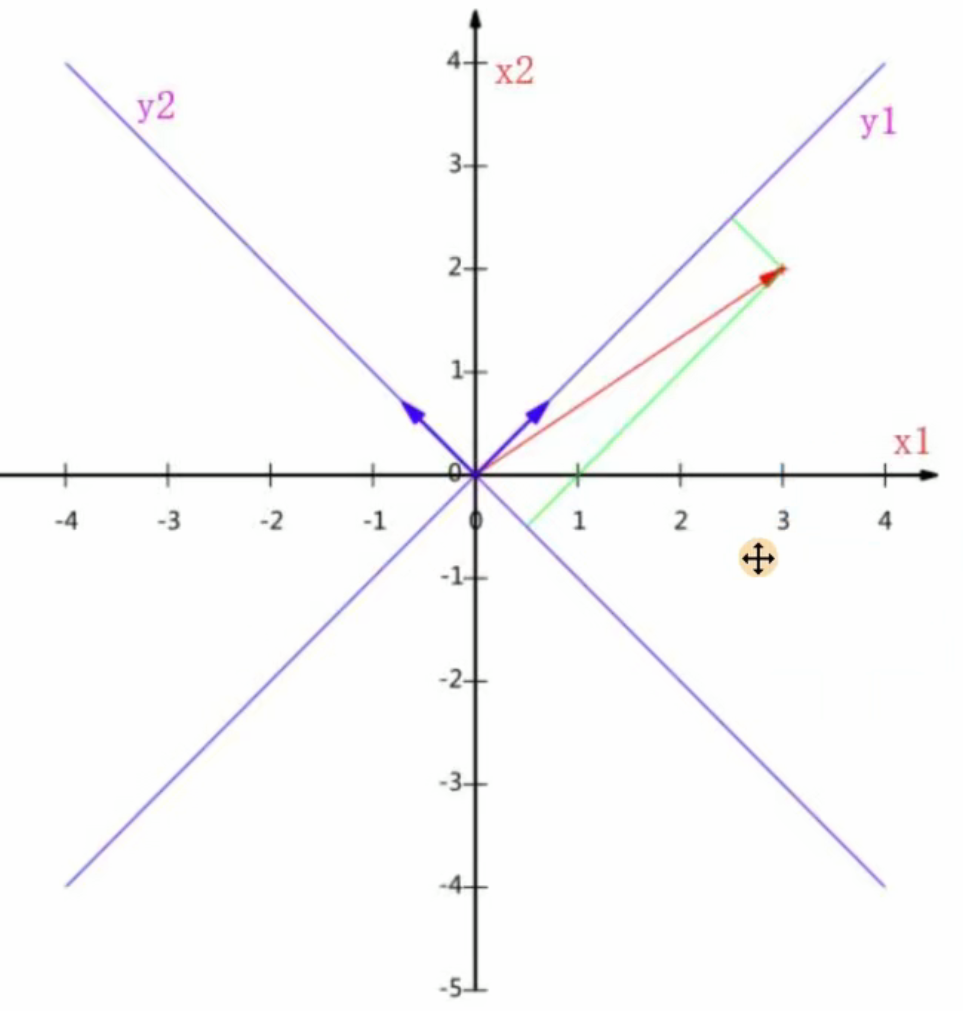
對于多維的

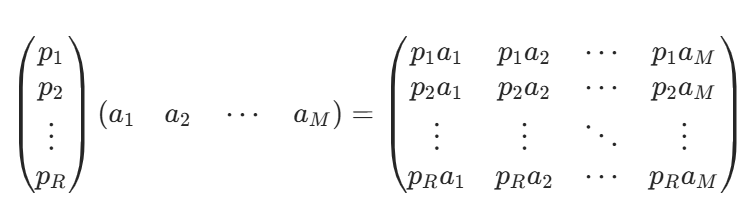
基變換的含義:

兩個矩陣相乘的意義是將右邊矩陣中的每一列列向量變換到左邊矩陣中每一行行向量為基所表示的空間中去。
抽象地說，一個矩陣可以表示一種線性變換。

卷積

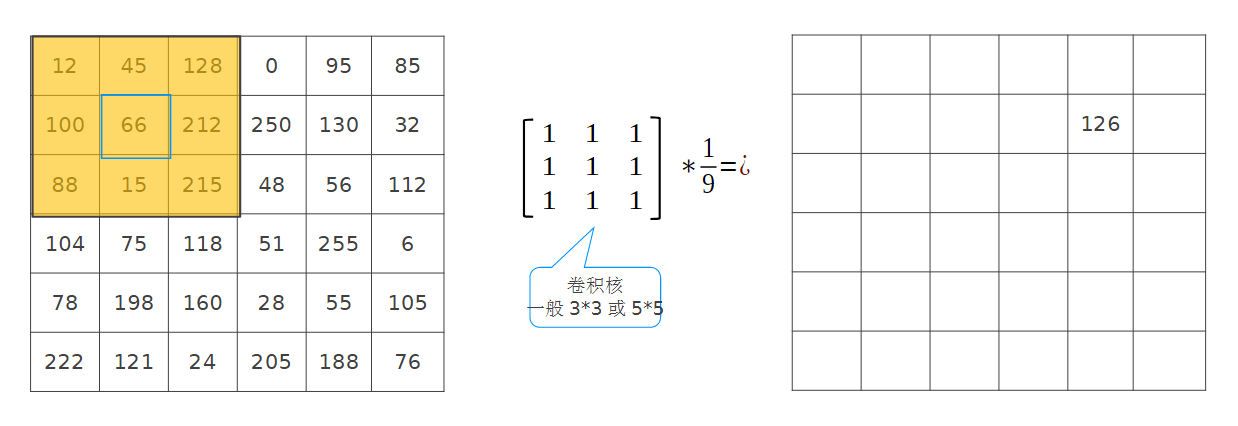
黃色填充和卷積核兩個矩陣相乘，空間發生了變換，

如何降維

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?

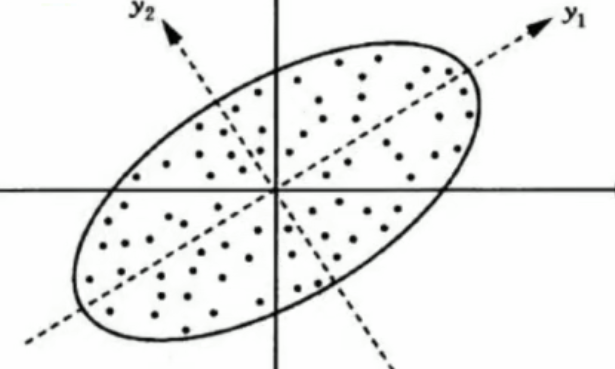
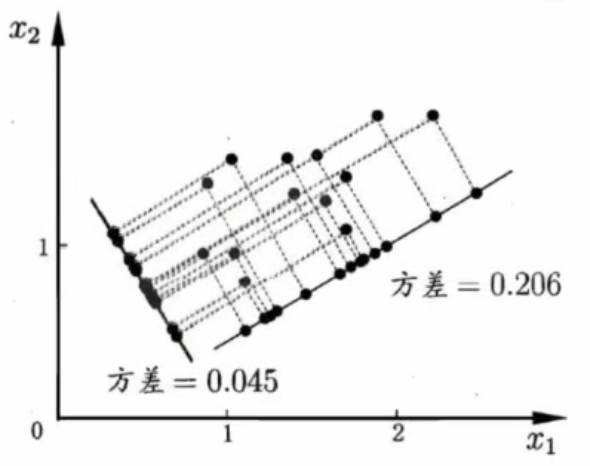
在求積y1 y2求最大方差

如何求最大方差

問題變為:
尋找一個一維基，使得所有數據變換為這個基上的坐標表示后，方差值最大。(對于二維變一維來說)

方案：找到方差次大

討論：就是關于方差次大與方差最大的關系是怎樣的|答案：線性無關（兩條線是垂直的關系）如果是交叉不是90垂直就是線性有關

協方差:

表征兩個字段之間的相關性。
當協方差為 0 時，表示兩個字段完全獨立。
目標:
利用協方差為 0，選擇另一組基，這組基的方向一定與第一組基正交。
推廣:
將一組 N 維向量降為 K 維（K 大于 0，小于 N），其目標是選擇 K 個單位（模為 1）正交基，使得原始數據變換到這組基上后，各字段兩兩間協方差為 0，而字段的方差則盡可能大（在正交的約束下，取最大的 K 個方差）
終極目標:
找到一組合的基。

注：降維是指降維的x的特征值

協方差矩陣:
假設我們有 a，b 兩個字段，組成矩陣：X

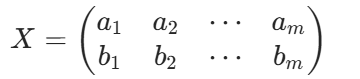
用 X 乘以其轉置，并乘以 1/m：

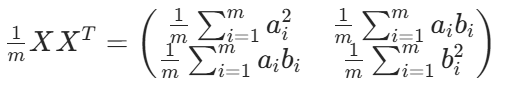
對角線是方差，反對角線是協方差

推廣:
對于更高維度的數據，上述結論依然成立。
找到一組合適的基。
方差:

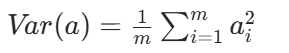
協方差:

目標:
除主對角線上的元素外，都為 0，并且方差從大到小排列。也就是協方差是0
終極目標:
找到一組合適的基。

協方差矩陣對角化:

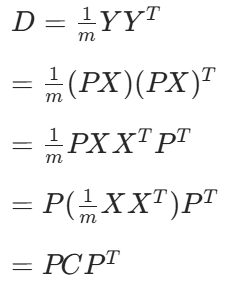
尋找一個矩陣 P，滿足 $PCP^{^{T}}$ 是一個對角矩陣，并且對角元素按從大到小依次排列，那么 P 的前 K 行就是要尋找的基，用 P 的前 K 行組成的矩陣乘以 X 就使得 X 從 N 維降到了 K 維并滿足上述優化條件。

原始數據: X —> 協方差矩陣: C
一組基按行組成的矩陣: P
基變換后的數據: Y—> 協方差矩陣: D
隱含信息: Y = PX

PCA 中的數學
協方差矩陣 C 對角化:

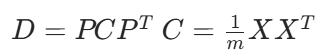
實對稱矩陣特性:

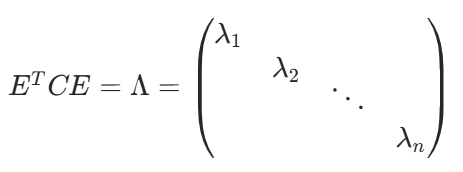
終極目標:
找到一組合適的基。

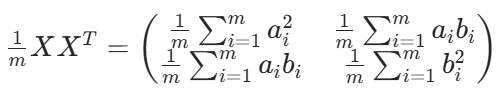
實對稱矩陣：矩陣轉置等于其本身
對角化：除主對角線之外其余元素均為 0
實對稱矩陣必可對角化

PCA 中的數學
終極目標找到:

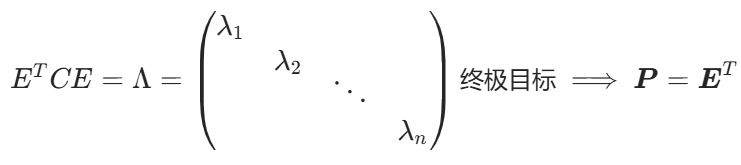
P 是協方差矩陣 C 的特征向量單位化后按行排列出的矩陣，其中每一行都是 C 的一個特征向量。

1. 執行第一步與第二步:
a b c d e

2. 計算協方差矩陣:

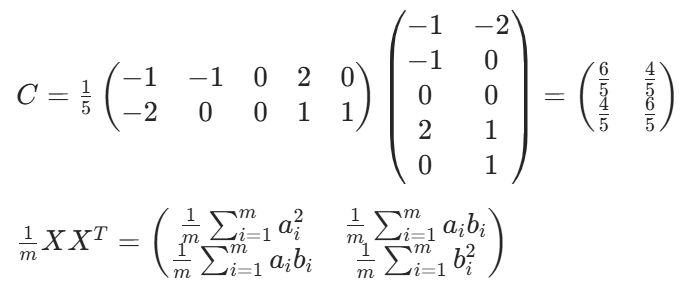
3. 計算協方差矩陣的特征值與特征向量:

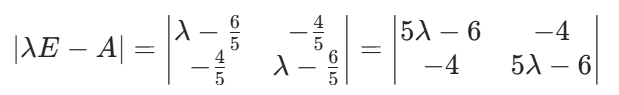
4. 矩陣P

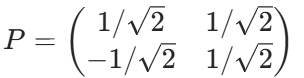
對角化驗證:

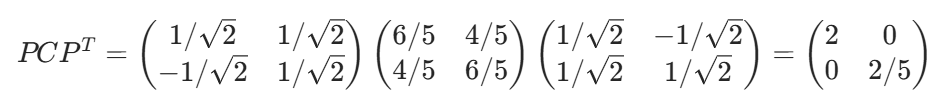
5. 降維

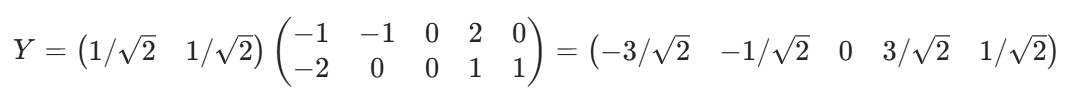
優點:
1. 計算方法簡單，容易實現。
2. 可以減少指標篩選的工作量。
3. 消除變量間的多重共線性。
4. 在一定程度上能減少噪聲數據。
缺點:
1. 特征必須是連續型變量。
2. 無法解釋降維后的數據是什么。
3. 貢獻率小的成分有可能更重要。

三·參數

sklearn.decomposition.PCA PCA(n_components=None, copy=True, whiten=False, svd_solver='auto', tol=0.0, iterated_power='auto', random_state=None)[source]

n_components：這個參數可以幫我們指定希望 PCA 降維后的特征維度數目。簡單來說：指定整數，表示要降維到的目標，【比如 10 維的數據，指定 n_components=5，表示將 10 維數據降維到 5 維】如果為小數，表示累計方差百分比。0.9

copy：類型：bool，True 或者 False，缺省時默認為 True。意義：表示是否在運行算法時，將原始訓練數據復制一份。若為 True，則運行 PCA 算法后，原始訓練數據的值不會有任何改變，因為是在原始數據的副本上進行運算；若為 False，則運行 PCA 算法后，原始訓練數據的值會改，因為是在原始數據上進行降維計算。【按默認為 True】

whiten：判斷是否進行白化。所謂白化，就是對降維后的數據的每個特征進行歸一化，讓方差都為 1.對于 PCA 降維本身來說，一般不需要白化。如果你 PCA 降維后有后續的數據處理動作，可以考慮白化。默認值是 False，即不進行白化。

svd_solver：即指定奇異值分解 SVD 的方法，由于特征分解是奇異值分解 SVD 的一個特例，一般的 PCA 庫都是基于 SVD 實現的。有 4 個可以選擇的值：{ 'auto', 'full', 'arpack', 'randomized' }。randomized 一般適用于數據量大，數據維度多同時主成分數目比例又較低的 PCA 降維，它使用了一些加快 SVD 的隨機算法。full 則是傳統意義上的 SVD，使用了 scipy 庫對應的實現。arpack 和 randomized 的適用場景類似，區別是 randomized 使用的是 scikit-learn 自己的 SVD 實現，而 arpack 直接使用了 scipy 庫的 sparse SVD 實現。默認是 auto，即

PCA 類會自己去在前面講到的三種算法里面去權衡，選擇一個合適的 SVD 算法來降維。一般來說，使用默認值就夠了。【按默認設置即可】

Attributes 屬性:
components_：array, shape (n_components, n_features) 指表示主成分系數矩陣
explained_variance_：降維后的各主成分的方差值。方差值越大，則說明越是重要的主成分。
explained_variance_ratio_：降維后的各主成分的方差值占總方差值的比例，這個比例越大，則越是重要的主成分。【一般看比例即可 >90%】

3、PCA 對象的方法

fit (X,y=None)
fit () 可以說是 scikit-learn 中通用的方法，每個需要訓練的算法都會有 fit () 方法，它其實就是算法中的 “訓練” 這一步驟。因為 PCA 是無監督學習算法，此處 y 自然等于 None。
fit (X)，表示用數據 X 來訓練 PCA 模型。
函數返回值：調用 fit 方法的對象本身。比如 pca.fit (X)，表示用 X 對 pca 這個對象進行訓練。

代碼

from sklearn.decomposition import PCA
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import classification_report# 數據讀取（CSV格式）
data = pd.read_csv("creditcard.csv")# 數據劃分（特征X和標簽y）
X = data.iloc[:, :-1]
y = data.iloc[:, -1]# ---------------------- PCA降維處理 ----------------------
# 實例化PCA對象（保留90%的方差）
pca = PCA(n_components=0.90)
pca.fit(X)  # 訓練PCA模型# 輸出PCA相關信息
print("=== PCA降維信息 ===")
print(f"保留的主成分數量: {pca.n_components_}")
print(f"解釋的方差占比總和: {sum(pca.explained_variance_ratio_):.4f}")
print("各主成分解釋的方差占比:", pca.explained_variance_ratio_)# 對數據進行降維轉換
new_x = pca.transform(X)# 劃分降維后的訓練集和測試集
x_train, x_test, y_train, y_test = train_test_split(new_x, y, test_size=0.2, random_state=0
)# 訓練邏輯回歸模型（手動設置class_weight處理類別不平衡）
classifier_pca = LogisticRegression(max_iter=1000,class_weight='balanced'  # 自動調整類別權重，提升少數類召回率
)
classifier_pca.fit(x_train, y_train)# 預測
train_pred_pca = classifier_pca.predict(x_train)
test_pred_pca = classifier_pca.predict(x_test)# 輸出分類報告（包含召回率等指標）
print("\n=== PCA降維后 - 訓練集分類報告 ===")
print(classification_report(y_train, train_pred_pca))  # 訓練集表現print("=== PCA降維后 - 測試集分類報告 ===")
print(classification_report(y_test, test_pred_pca))    # 測試集表現# ---------------------- 不使用PCA降維 ----------------------
# 直接劃分原始數據
x_train_no_pca, x_test_no_pca, y_train_no_pca, y_test_no_pca = train_test_split(X, y, test_size=0.2, random_state=0
)# 訓練邏輯回歸模型（不降維，同樣設置class_weight）
classifier_no_pca = LogisticRegression(max_iter=1000,class_weight='balanced'
)
classifier_no_pca.fit(x_train_no_pca, y_train_no_pca)# 預測
train_pred_no_pca = classifier_no_pca.predict(x_train_no_pca)
test_pred_no_pca = classifier_no_pca.predict(x_test_no_pca)# 輸出分類報告
print("\n=== 不使用PCA - 訓練集分類報告 ===")
print(classification_report(y_train_no_pca, train_pred_no_pca))print("=== 不使用PCA - 測試集分類報告 ===")
print(classification_report(y_test_no_pca, test_pred_no_pca))

1. 導入所需庫

python

運行

from sklearn.decomposition import PCA  # 導入PCA降維工具
import pandas as pd  # 數據處理庫
from sklearn.model_selection import train_test_split  # 數據拆分工具
from sklearn.linear_model import LogisticRegression  # 邏輯回歸模型
from sklearn.metrics import classification_report  # 分類評估報告工具

2. 數據讀取與劃分

python

運行

# 讀取CSV格式的信用卡數據
data = pd.read_csv("creditcard.csv")# 劃分特征X和標簽y（假設最后一列是目標變量，即是否欺詐）
X = data.iloc[:, :-1]  # 取所有行，除最后一列外的所有列作為特征
y = data.iloc[:, -1]   # 取所有行的最后一列作為標簽

3. PCA 降維處理部分

python

運行

# 實例化PCA對象，設置保留90%的方差（即降維后保留原數據90%的信息）
pca = PCA(n_components=0.90)
pca.fit(X)  # 用原始特征數據訓練PCA模型，學習主成分# 輸出PCA降維的相關信息
print("=== PCA降維信息 ===")
print(f"保留的主成分數量: {pca.n_components_}")  # 實際保留的主成分個數
print(f"解釋的方差占比總和: {sum(pca.explained_variance_ratio_):.4f}")  # 總方差保留比例
print("各主成分解釋的方差占比:", pca.explained_variance_ratio_)  # 每個主成分的方差占比# 對原始特征數據進行降維轉換，得到新的低維特征
new_x = pca.transform(X)

4. 降維后的數據建模與評估

python

運行

# 將降維后的數據集拆分為訓練集(80%)和測試集(20%)，固定隨機種子保證結果可復現
x_train, x_test, y_train, y_test = train_test_split(new_x, y, test_size=0.2, random_state=0
)# 初始化邏輯回歸模型，設置最大迭代次數為1000（確保收斂）
# class_weight='balanced'用于處理類別不平衡問題（信用卡欺詐數據中欺詐樣本通常很少）
classifier_pca = LogisticRegression(max_iter=1000,class_weight='balanced'
)
classifier_pca.fit(x_train, y_train)  # 用降維后的訓練集訓練模型# 分別對訓練集和測試集進行預測
train_pred_pca = classifier_pca.predict(x_train)
test_pred_pca = classifier_pca.predict(x_test)# 輸出分類報告，包含精確率、召回率、F1分數等指標，評估模型表現
print("\n=== PCA降維后 - 訓練集分類報告 ===")
print(classification_report(y_train, train_pred_pca))
print("=== PCA降維后 - 測試集分類報告 ===")
print(classification_report(y_test, test_pred_pca))

5. 不使用 PCA 降維的對比實驗

python

運行

# 直接對原始特征數據進行拆分，參數與前面保持一致，確保對比公平
x_train_no_pca, x_test_no_pca, y_train_no_pca, y_test_no_pca = train_test_split(X, y, test_size=0.2, random_state=0
)# 初始化另一個邏輯回歸模型，參數與降維實驗保持一致
classifier_no_pca = LogisticRegression(max_iter=1000,class_weight='balanced'
)
classifier_no_pca.fit(x_train_no_pca, y_train_no_pca)  # 用原始特征訓練模型# 分別對訓練集和測試集進行預測
train_pred_no_pca = classifier_no_pca.predict(x_train_no_pca)
test_pred_no_pca = classifier_no_pca.predict(x_test_no_pca)# 輸出分類報告，與降維后的結果進行對比
print("\n=== 不使用PCA - 訓練集分類報告 ===")
print(classification_report(y_train_no_pca, train_pred_no_pca))
print("=== 不使用PCA - 測試集分類報告 ===")
print(classification_report(y_test_no_pca, test_pred_no_pca))