知識蒸餾 - 各類概率分布

flyfish
請添加圖片描述

一、離散概率分布

離散分布描述的是取值為離散值（如0,1,2,…）的隨機變量的概率規律，通常用概率質量函數（PMF） 表示某一取值的概率。

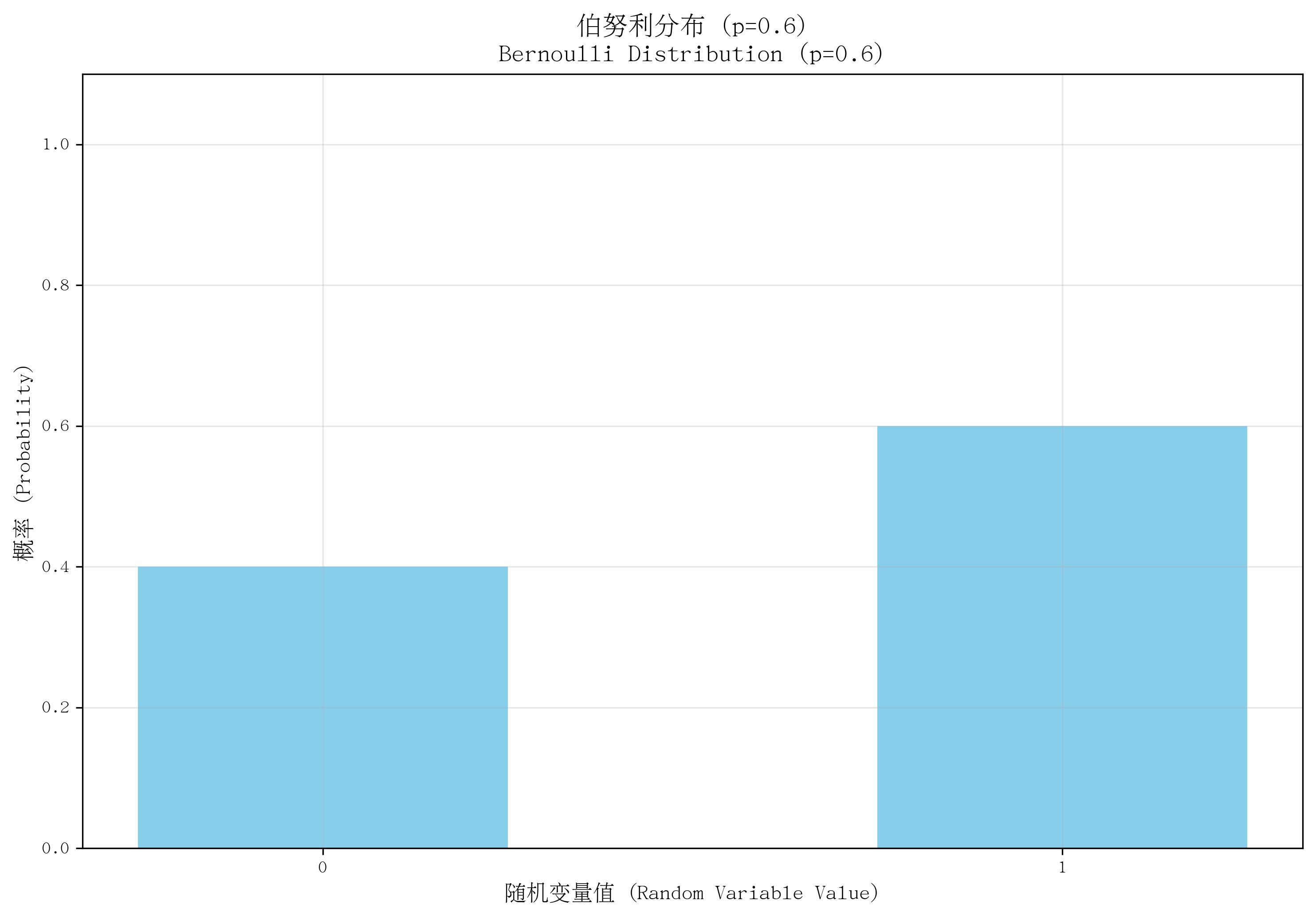
1. 伯努利分布（Bernoulli Distribution）

定義：描述單次隨機試驗的結果，僅有兩種可能（“成功”或“失敗”），是最簡單的離散分布。
核心參數：成功概率 $p$ （ $\leq p \leq 1$ ），失敗概率為 $1 ? p$ 。
概率質量函數（PMF）：
$P(X=k) = p^k (1-p)^{1-k}$ ，其中 $k = 0$ （失敗）或 $k = 1$ （成功）。
適用場景：單次試驗的二元結果，如“拋一次硬幣是否正面朝上”“一次抽獎是否中獎”。
特點：僅含一次試驗，結果非0即1；是所有離散分布的基礎，多次獨立伯努利試驗可擴展為其他分布（如二項分布）。

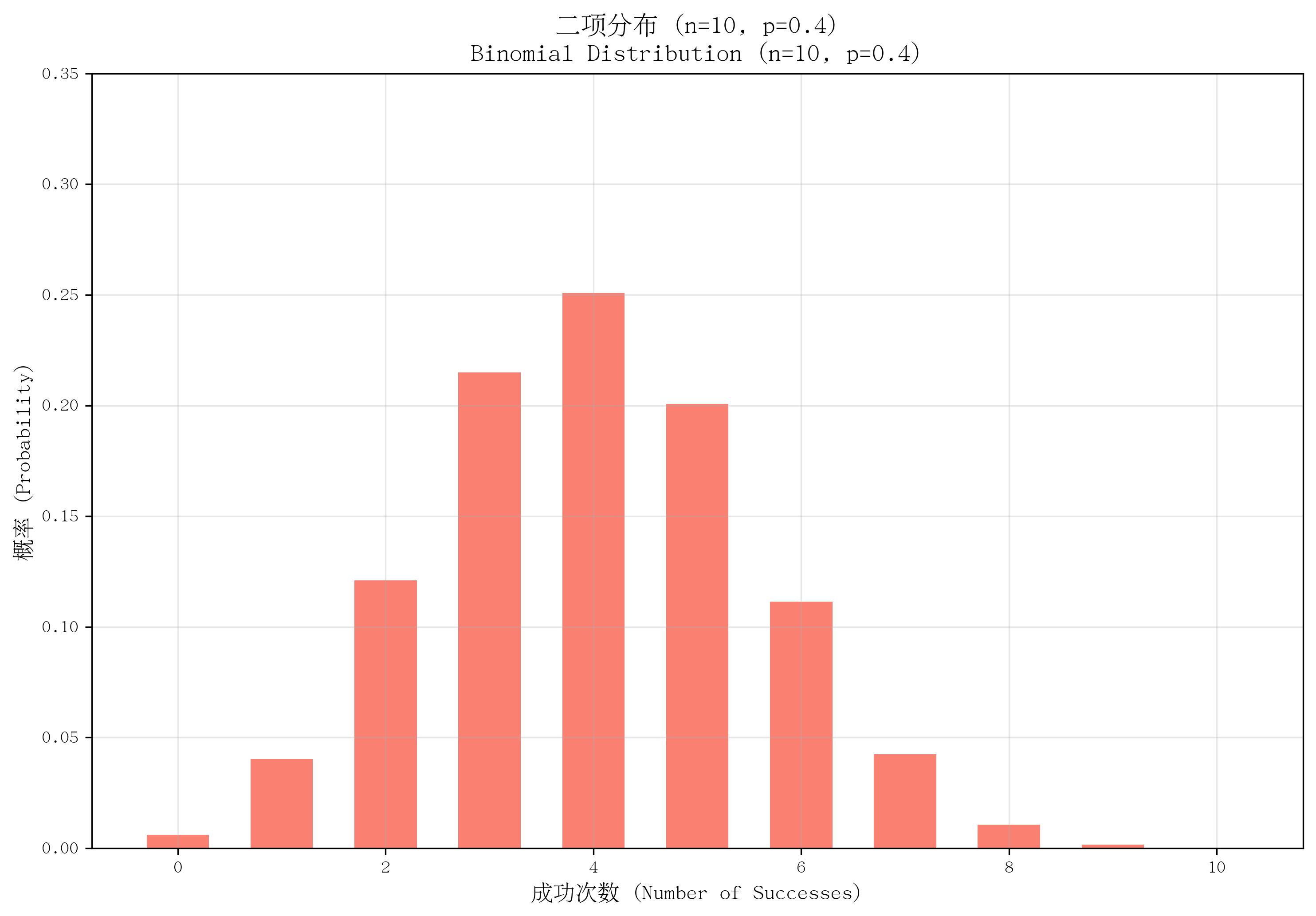
2. 二項分布（Binomial Distribution）

定義：描述 $n$ 次獨立重復的伯努利試驗中，“成功”次數的概率分布。
核心參數：試驗次數 $n$ （正整數）、單次成功概率 $p$ （ $\leq p \leq 1$ ）。
概率質量函數（PMF）：
$\binom{n}{k} p^k (1-p)^{n-k}$ ，其中 $k = 0, 1, ..., n$ ， $(nk)\binom{n}{k}$ 為組合數（從n次中選k次成功的方式數）。
適用場景：多次獨立試驗的成功次數，如“拋10次硬幣正面朝上的次數”“100件產品中不合格品的數量”。
特點：試驗獨立且每次成功概率相同；當 $n = 1$ 時，退化為伯努利分布；均值為 $n p$ ，方差為 $n p (1 ? p)$ 。

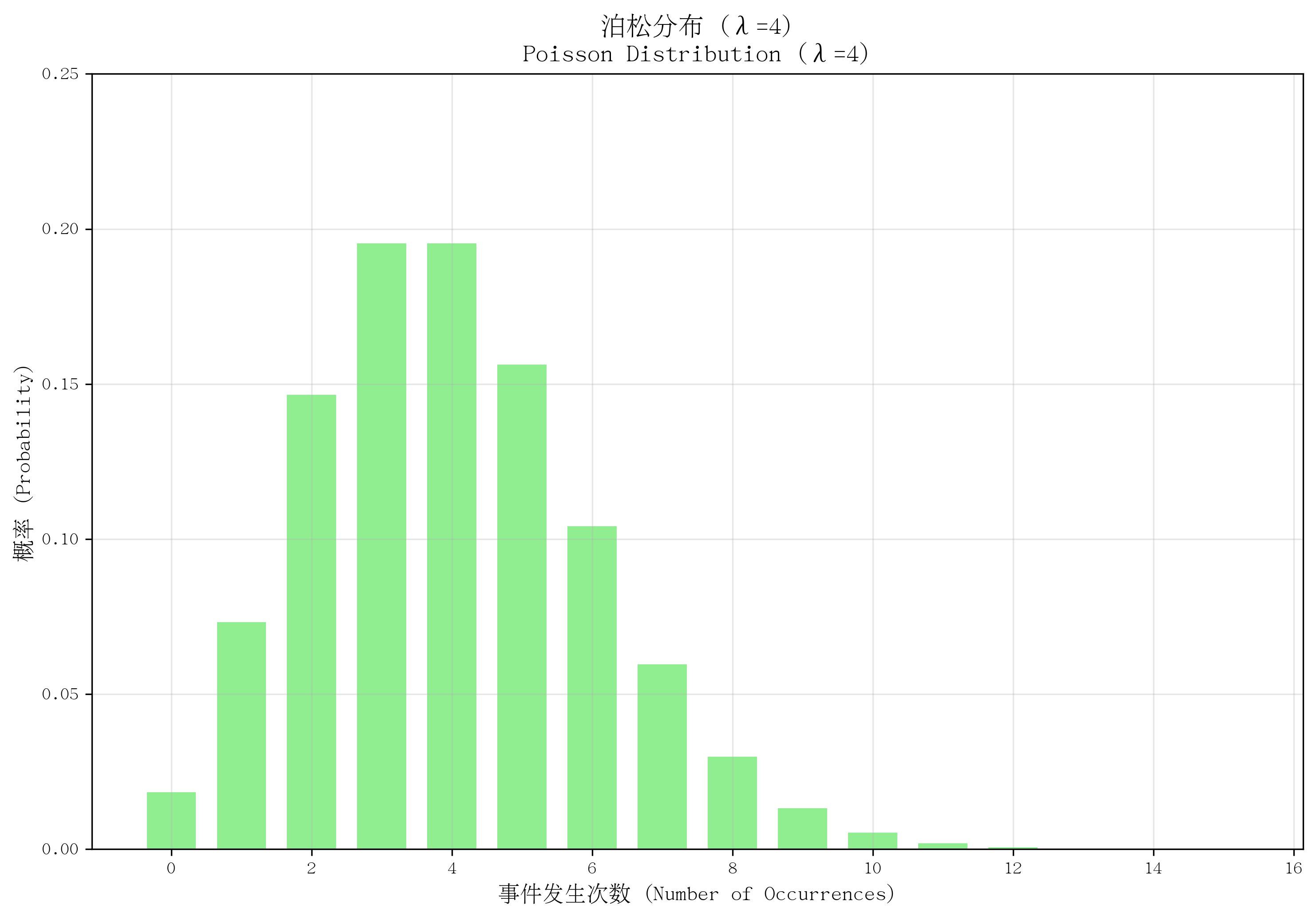
3. 泊松分布（Poisson Distribution）

定義：描述“一定時間/空間內，某隨機事件發生次數”的概率分布。
核心參數：發生率 $λ\lambda$ （ $λ>0\lambda > 0$ ，表示單位時間/空間內事件的平均發生次數）。
概率質量函數（PMF）：
$\frac{\lambda^k e^{-\lambda}}{k!}$ ，其中 $k = 0, 1, 2, ...$ （事件發生次數）， $e$ 為自然常數， $k!$ 為k的階乘。
適用場景：稀有事件的發生次數，如“1小時內客服接到的電話次數”“1平方米布料上的瑕疵數”“一天內醫院的急診人數”。
特點：事件獨立發生，且發生率恒定；均值和方差均為 $λ\lambda$ ；當二項分布中 $n$ 很大、 $p$ 很小時（ $\approx \lambda$ ），可近似為泊松分布。

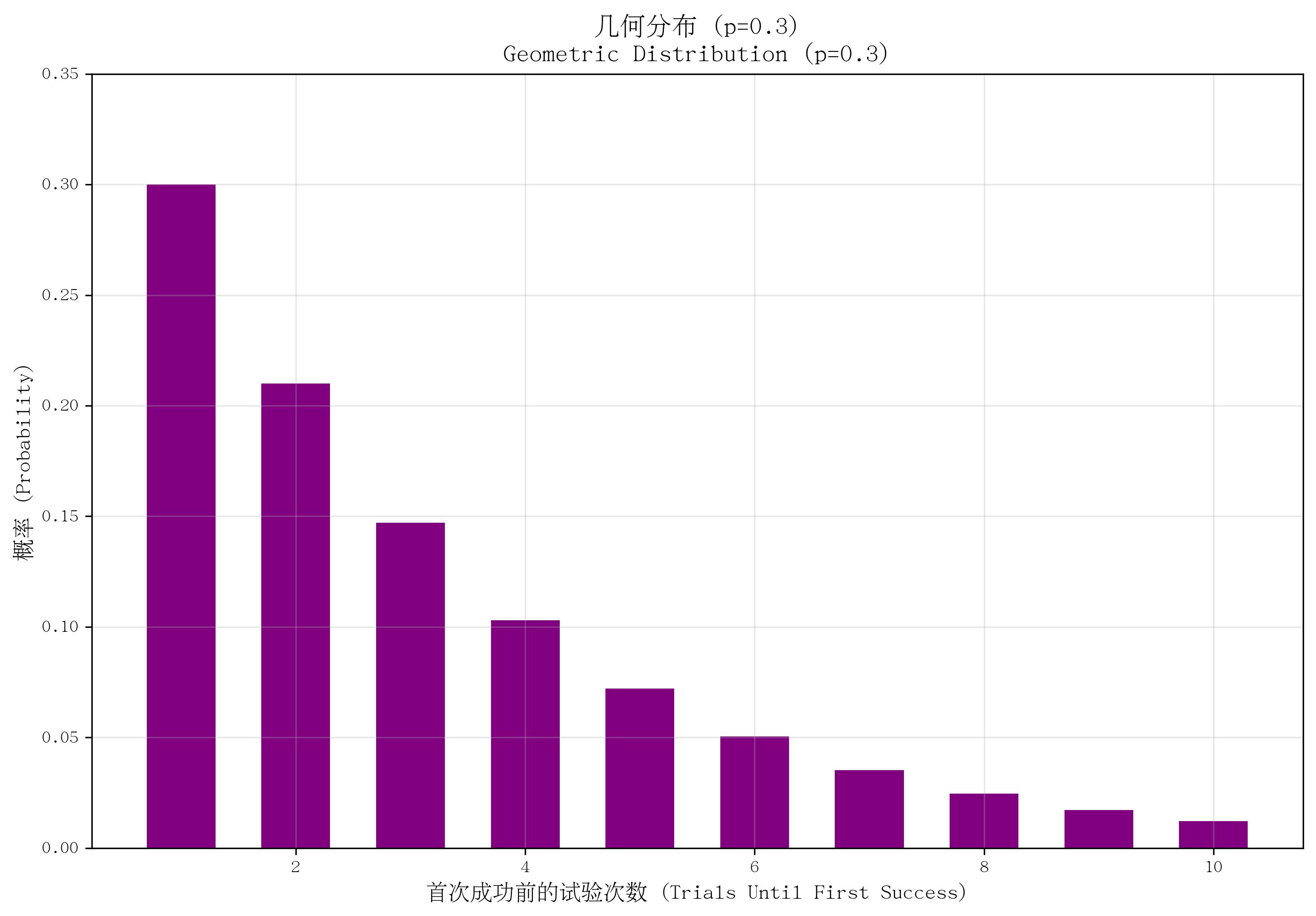
4. 幾何分布（Geometric Distribution）

定義：描述“在一系列獨立伯努利試驗中，首次獲得成功所需要的試驗次數”的概率分布。
核心參數：單次試驗成功概率 $p$ （ $\leq 1$ ）。
概率質量函數（PMF）：
$P(X=k) = (1-p)^{k-1} p$ ，其中 $k = 1, 2, ...$ （首次成功時的試驗次數，至少為1）。
適用場景：首次成功前的試驗次數，如“首次命中目標前的射擊次數”“首次抽到紅球前的抽獎次數”。
特點：無記憶性（即“前k次失敗不影響后續成功的概率”）；均值為 $1/ p$ （平均需要 $1/ p$ 次試驗才能首次成功），方差為 $1-p)/p^2$ 。

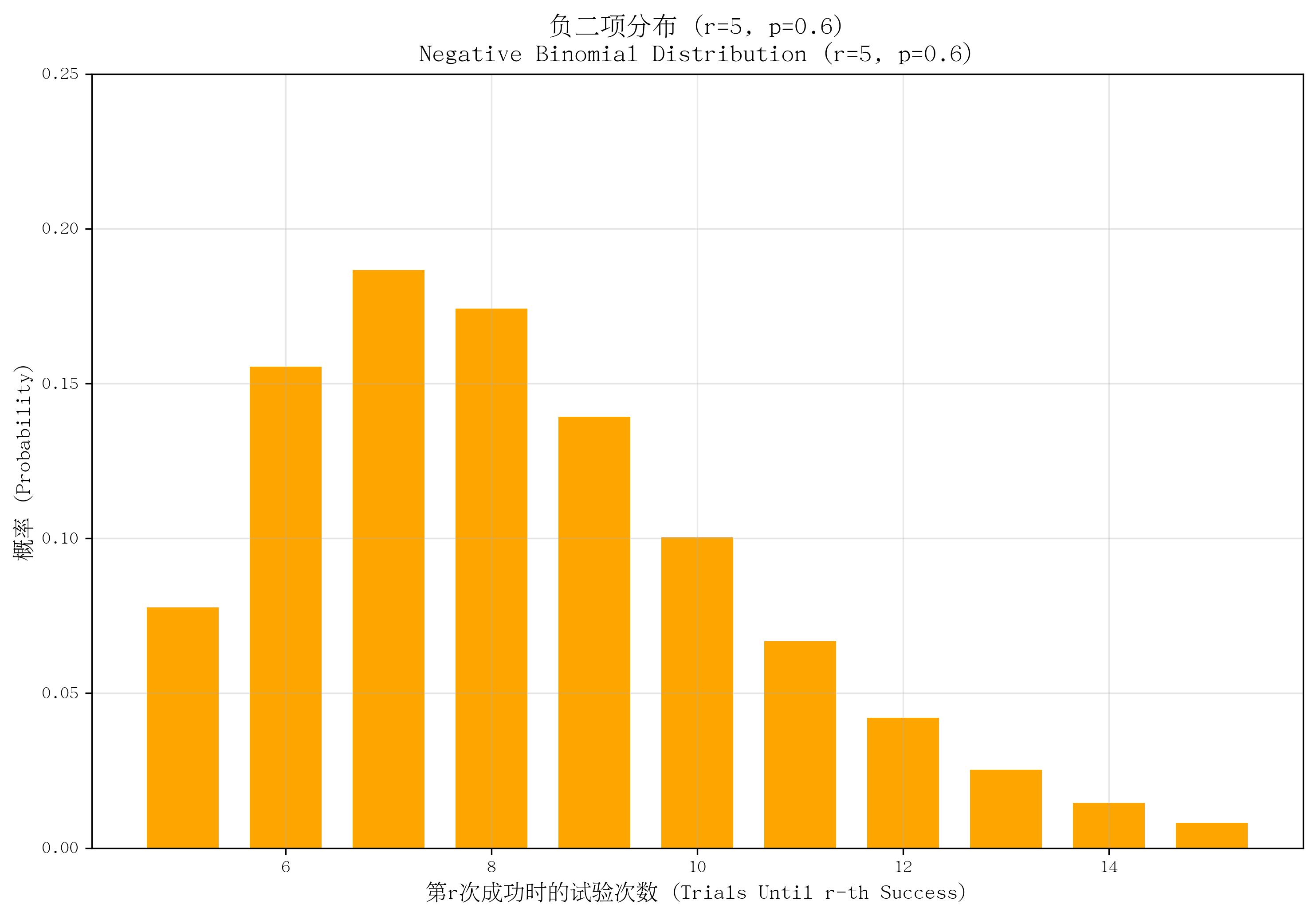
5. 負二項分布（Negative Binomial Distribution）

定義：描述“在一系列獨立伯努利試驗中，獲得第 $r$ 次成功時所需要的總試驗次數”的概率分布（幾何分布是其 $r = 1$ 時的特例）。
核心參數：目標成功次數 $r$ （正整數）、單次試驗成功概率 $p$ （ $\leq 1$ ）。
概率質量函數（PMF）：
$\binom{k-1}{r-1} p^r (1-p)^{k-r}$ ，其中 $k = r, r + 1, ...$ （總試驗次數，至少為 $r$ ）。
適用場景：需要多次成功的試驗次數，如“第5次命中目標時的總射擊次數”“第3次賣出產品時的總客戶接待數”。
特點：可視為 $r$ 個獨立幾何分布的和；均值為 $r / p$ ，方差為 $r(1-p)/p^2$ 。

二、連續概率分布

連續分布描述的是取值為連續區間（如實數域）的隨機變量的概率規律，通常用概率密度函數（PDF） 表示某一區間內的概率密度（需通過積分計算區間概率）。

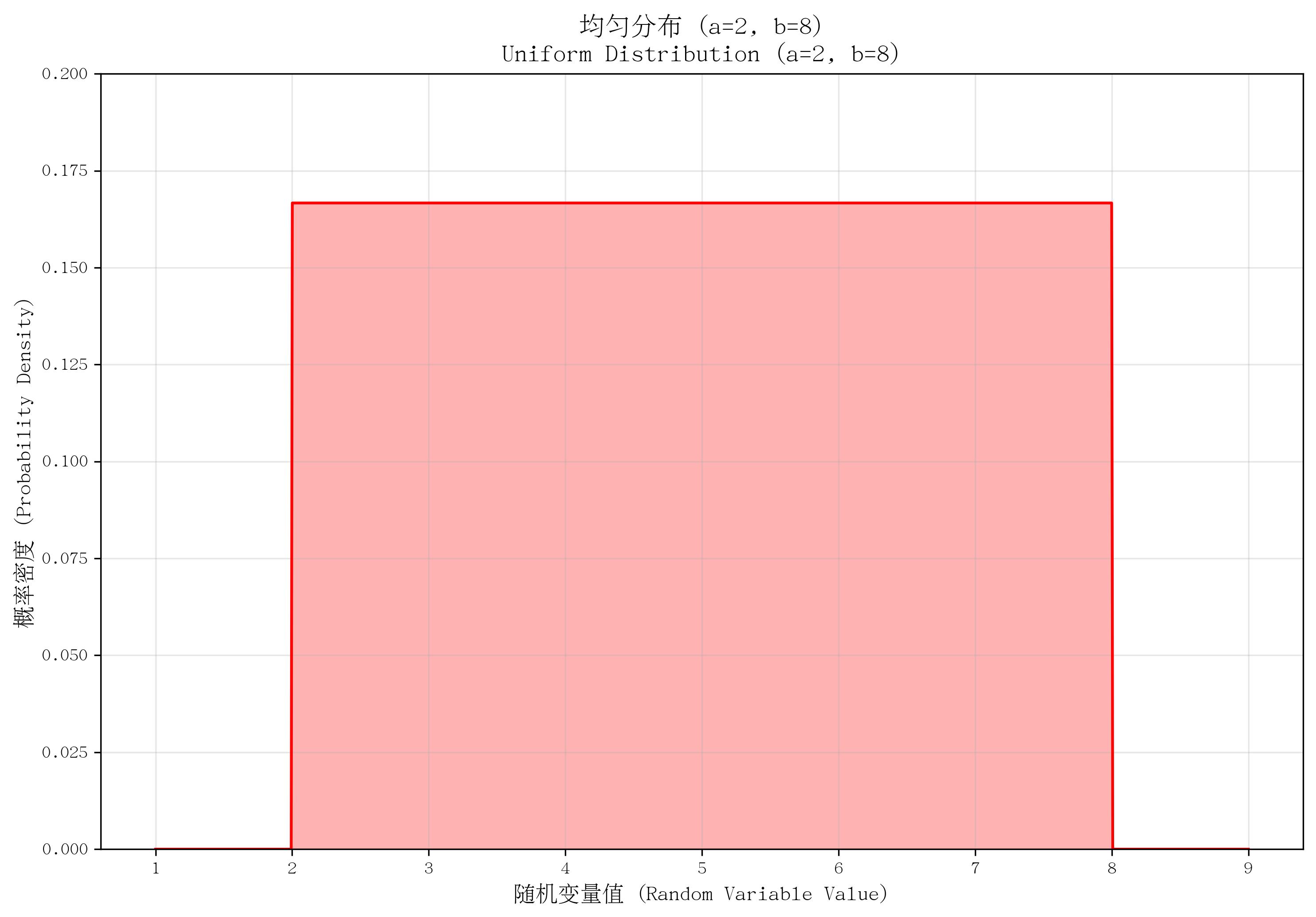
6. 均勻分布（Uniform Distribution）

定義：描述“隨機變量在區間 ([a,b]) 內所有取值的概率密度均相等”的分布。
核心參數：區間下界 $a$ 和上界 $b$ （ $a < b$ ）。
概率密度函數（PDF）：
$\begin{cases} \frac{1}{b-a} & \text{若 } a \leq x \leq b \\ 0 & \text{其他} \end{cases}$
適用場景：等可能結果的連續取值，如“隨機選擇的時間點在[0,24小時]內的分布”“隨機測量的誤差在[-0.5,0.5]內的分布”。
特點：概率密度恒定（矩形分布）；均值為 $(a + b) /2$ ，方差為 $b-a)^2/12$ ；區間內任意子區間的概率與子區間長度成正比。

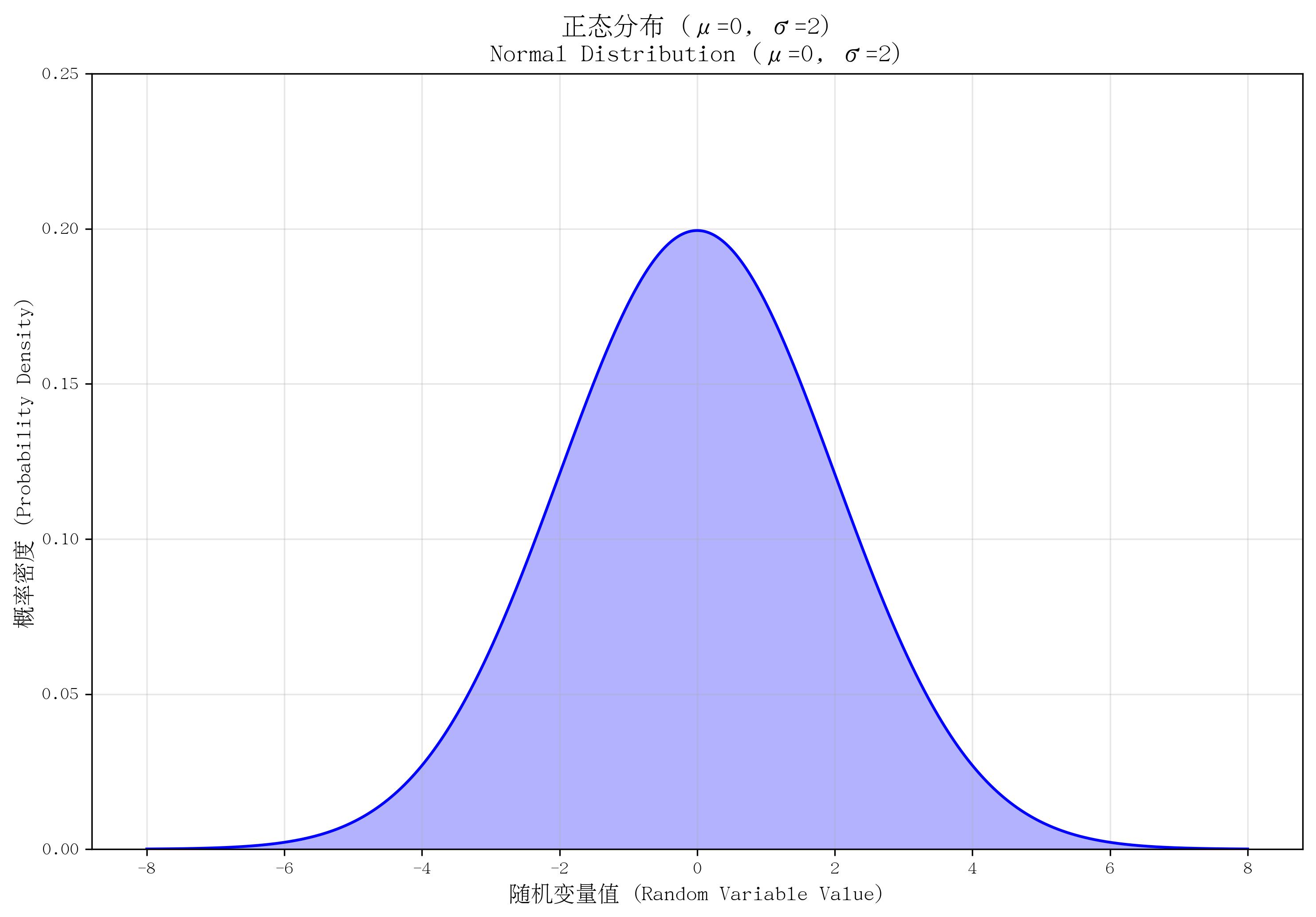
7. 正態分布（Normal Distribution）

定義：又稱“高斯分布”，是自然界最常見的連續分布，呈對稱的鐘形曲線。
核心參數：均值 $μ\mu$ （曲線中心位置）、標準差 $σ\sigma$ （曲線寬窄， $σ>0\sigma > 0$ ）。
概率密度函數（PDF）：
$\frac{1}{\sigma \sqrt{2\pi}} e^{-\frac{(x-\mu)^2}{2\sigma^2}}$ ，其中 $x$ 為任意實數， $e$ 為自然常數。
適用場景：大量獨立隨機因素影響的結果，如“人群身高/體重分布”“測量誤差分布”“考試分數分布”。
特點：對稱性（關于 $x=μx=\mu$ 對稱）；“3σ法則”（約99.7%的取值落在 $[μ?3σ,μ+3σ][\mu-3\sigma, \mu+3\sigma]$ 內）；中心極限定理表明，大量獨立隨機變量的和近似服從正態分布；標準正態分布（ $μ=0,σ=1\mu=0, \sigma=1$ ）是基礎，可通過標準化轉換（ $Z=(X?μ)/σZ=(X-\mu)/\sigma$ ）將任意正態分布轉化為標準正態分布。

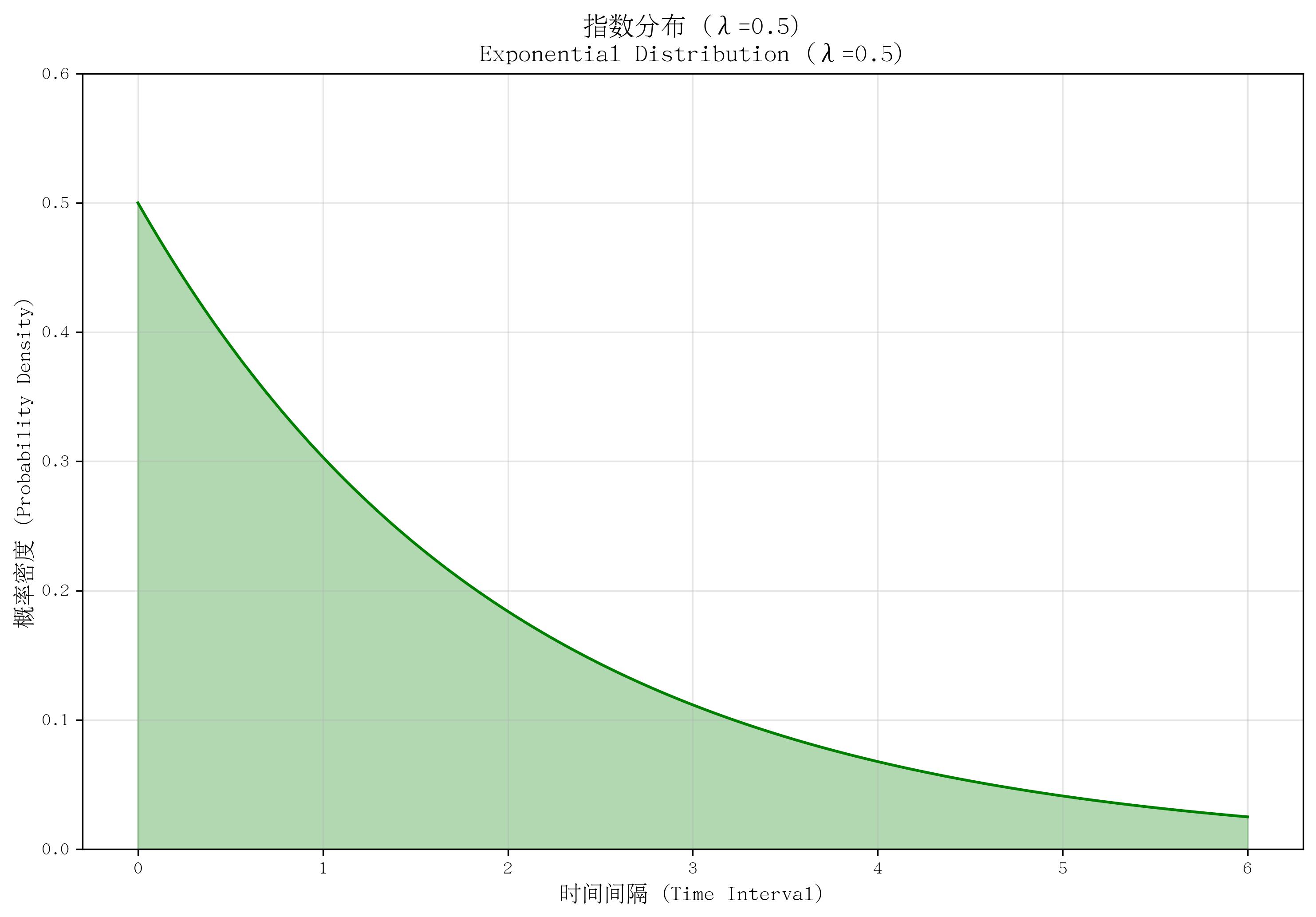
8. 指數分布（Exponential Distribution）

定義：描述“兩次獨立隨機事件發生的時間間隔”的概率分布（與泊松分布對應：泊松分布描述事件發生次數，指數分布描述事件間隔時間）。
核心參數：率參數 $λ\lambda$ （ $λ>0\lambda > 0$ ，表示單位時間內事件的平均發生次數，與泊松分布的 $λ\lambda$ 一致）。
概率密度函數（PDF）：
$\begin{cases} \lambda e^{-\lambda x} & \text{若 } x \geq 0 \\ 0 & \text{若 } x < 0 \end{cases}$
適用場景：事件間隔時間，如“兩次設備故障的時間間隔”“兩次客戶到達的時間間隔”“電池壽命”。
特點：無記憶性（即“已使用t小時的設備，剩余壽命與新設備相同”）；均值為 $1/λ1/\lambda$ （平均間隔時間），方差為 $1/λ21/\lambda^2$ ；取值范圍為非負實數。

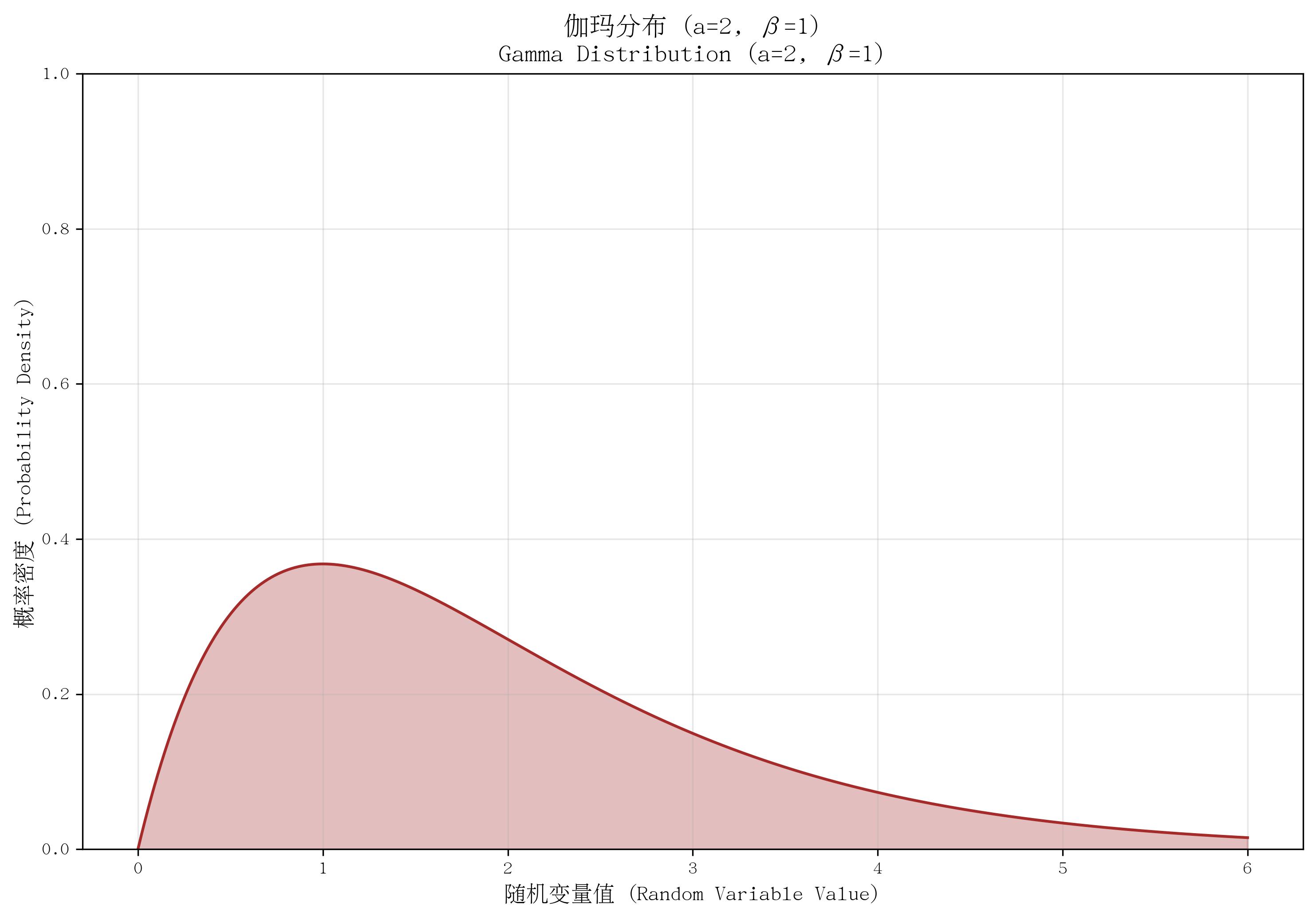
9. 伽瑪分布（Gamma Distribution）

定義：描述“多個獨立指數分布變量的總和”的概率分布（指數分布是其形狀參數 $a = 1$ 時的特例）。
核心參數：形狀參數 $a$ （ $a > 0$ ，可理解為“事件次數”）、率參數 $β\beta$ （ $β>0\beta > 0$ ，與指數分布的 $λ\lambda$ 類似）。
概率密度函數（PDF）：
$\begin{cases} \frac{\beta^a}{\Gamma(a)} x^{a-1} e^{-\beta x} & \text{若 } x \geq 0 \\ 0 & \text{若 } x < 0 \end{cases}$
其中 $Γ(a)\Gamma(a)$ 為伽瑪函數（當 $a$ 為整數時， $Γ(a)=(a?1)!\Gamma(a)=(a-1)!$ ）。
適用場景：多個事件間隔的總和，如“3次電話呼叫的總時間”“5個零件的總壽命”；當 $a$ 為整數時，也稱為“愛爾朗分布”（Erlang Distribution），常用于排隊論。
特點：形狀隨 $a$ 變化（ $a$ 增大時逐漸接近正態分布）；均值為 $a/βa/\beta$ ，方差為 $a/β2a/\beta^2$ 。

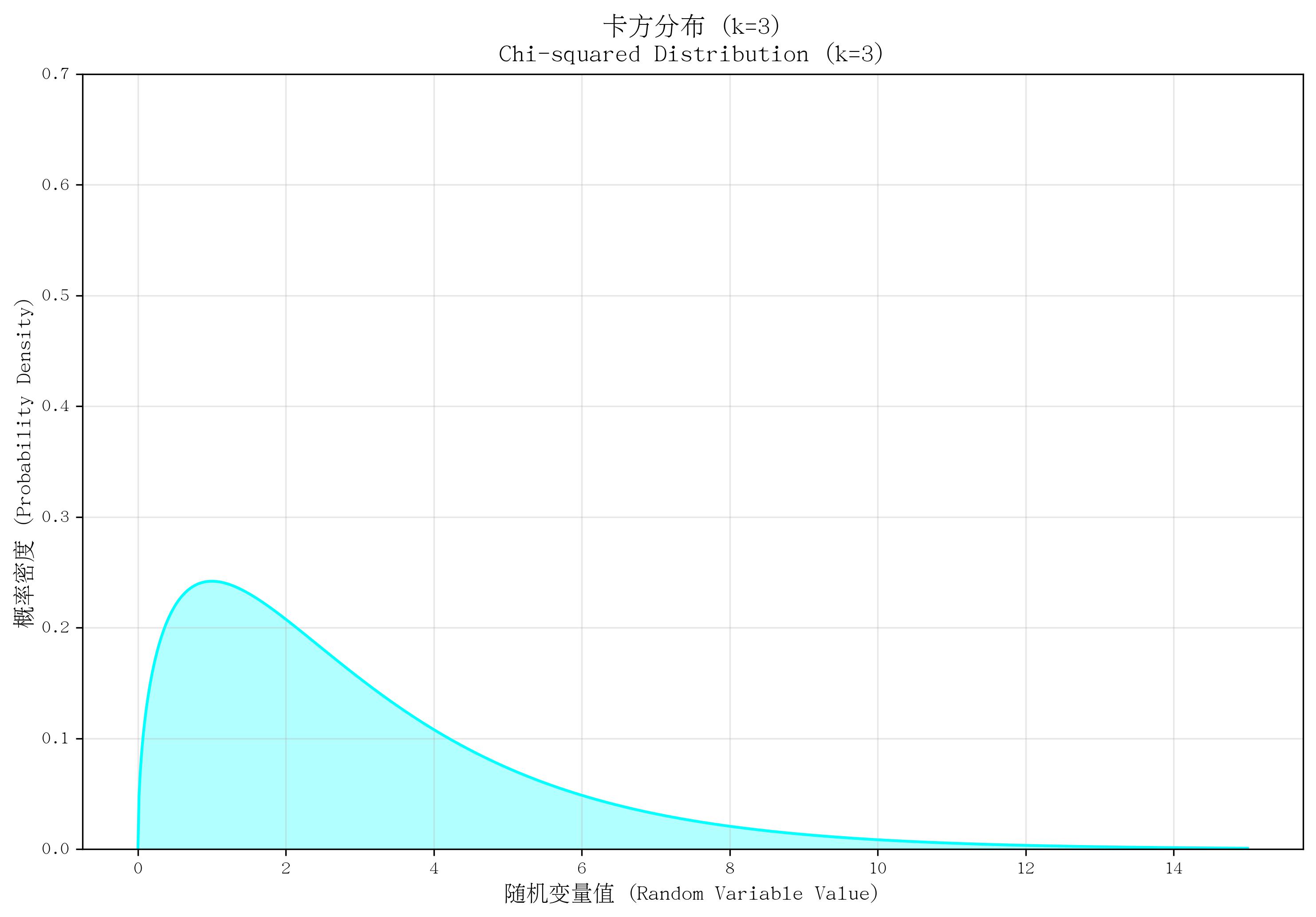
10. 卡方分布（Chi-Squared Distribution）

定義：描述“k個獨立標準正態變量的平方和”的概率分布（是伽瑪分布的特例：當形狀參數 $a = k /2$ 、率參數 $β=1/2\beta=1/2$ 時）。
核心參數：自由度 $k$ （正整數，對應標準正態變量的個數）。
概率密度函數（PDF）：
$\begin{cases} \frac{1}{2^{k/2} \Gamma(k/2)} x^{(k/2)-1} e^{-x/2} & \text{若 } x \geq 0 \\ 0 & \text{若 } x < 0 \end{cases}$
適用場景：統計檢驗中，如“方差的假設檢驗”“擬合優度檢驗”“獨立性檢驗”；是t分布和F分布的基礎。
特點：取值非負，右偏分布（隨 $k$ 增大逐漸對稱）；均值為 $k$ ，方差為 $2 k$ ；若 $\sim \chi^2(k_1)$ 且 $\sim \chi^2(k_2)$ ，則 $\sim \chi^2(k_1+k_2)$ （可加性）。

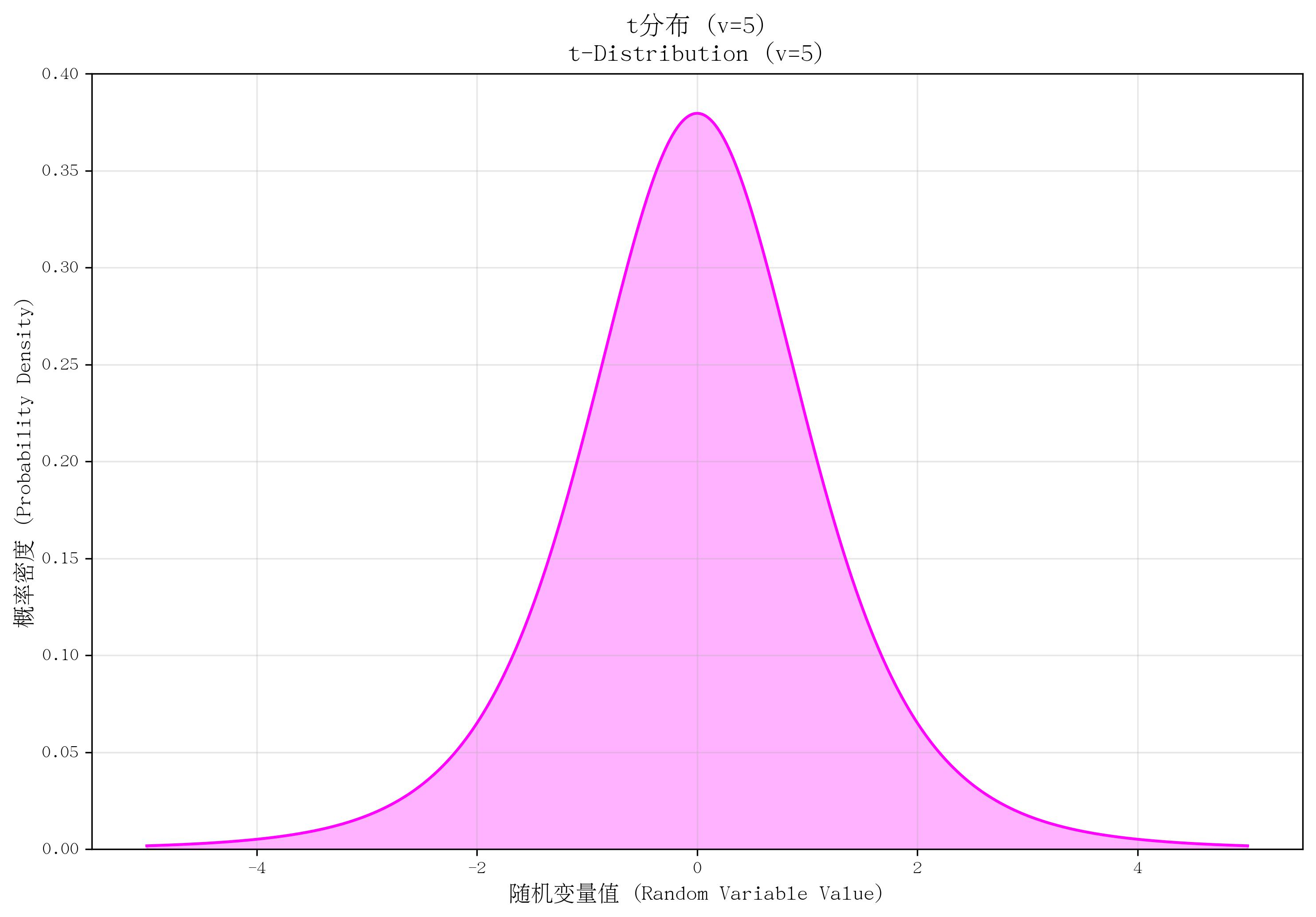
11. t分布（t-Distribution）

定義：描述“小樣本均值標準化后”的概率分布，當總體標準差未知時，用樣本標準差替代后推導得到。
核心參數：自由度 $v$ （正整數，通常為樣本量減1， $v = n ? 1$ ）。
概率密度函數（PDF）：
$\frac{\Gamma((v+1)/2)}{\sqrt{v\pi} \Gamma(v/2)} \left(1 + \frac{x^2}{v}\right)^{-(v+1)/2}$ ，其中 $x$ 為任意實數。
適用場景：小樣本（ $n < 30$ ）的均值檢驗，如“小樣本下總體均值的區間估計”“單樣本t檢驗”“兩獨立樣本t檢驗”。
特點：形狀類似正態分布，但尾部更厚（對極端值更敏感）；隨自由度 $v$ 增大，逐漸接近標準正態分布（ $\to \infty$ 時完全一致）；均值為0（ $v > 1$ 時），方差為 $v / (v ? 2)$ （ $v > 2$ 時）。

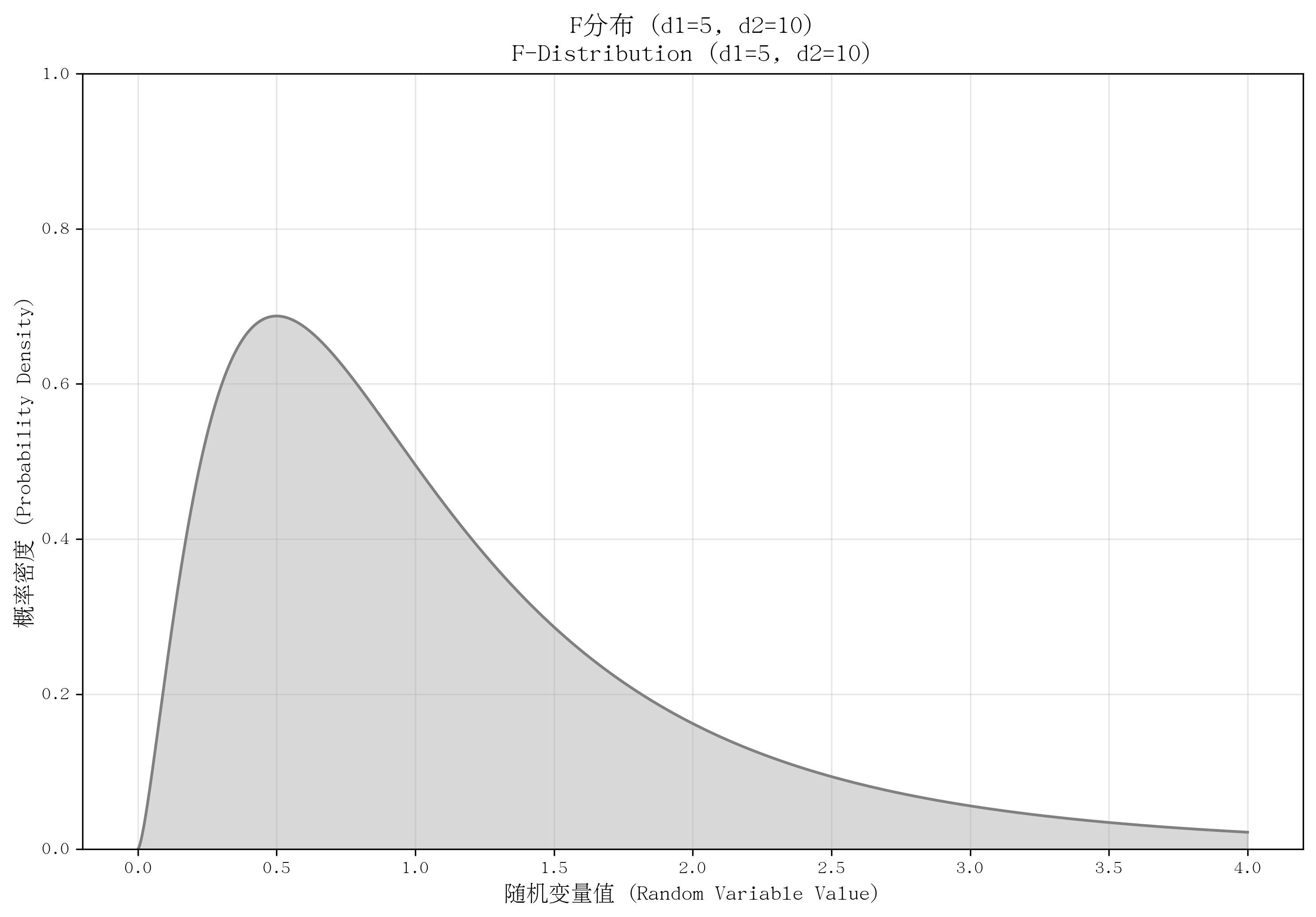
12. F分布（F-Distribution）

定義：描述“兩個獨立卡方分布變量分別除以各自自由度后的比值”的概率分布。
核心參數：分子自由度 $d_1$ 和分母自由度 $d_2$ （均為正整數）。
概率密度函數（PDF）：
$\begin{cases} \frac{\Gamma((d_1+d_2)/2)}{\Gamma(d_1/2)\Gamma(d_2/2)} \left(\frac{d_1}{d_2}\right)^{d_1/2} x^{(d_1/2)-1} \left(1 + \frac{d_1}{d_2}x\right)^{-(d_1+d_2)/2} & \text{若 } x \geq 0 \\ 0 & \text{若 } x < 0 \end{cases}$
適用場景：方差比較，如“方差分析（ANOVA）”（檢驗多組均值是否有差異）、“兩總體方差比的假設檢驗”。
特點：取值非負，右偏分布；形狀由兩個自由度共同決定；若 $\sim F(d_1,d_2)$ ，則 $\sim F(d_2,d_1)$ （倒數性質）。

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats# 設置中文顯示
#plt.rcParams["font.family"] = ["SimHei"]
plt.rcParams["font.family"] = ['AR PL UMing CN']#Linux
plt.rcParams["axes.unicode_minus"] = False  # 解決負號顯示問題def save_distribution_plot(plot_func, params, title_cn, title_en, x_label, y_label,filename_cn, filename_en, params_str, is_discrete=True):"""生成并保存分布圖像的通用函數（不含公式）"""plt.figure(figsize=(10, 7))plot_func(*params)# 標題組合中英文plt.title(f"{title_cn}\n{title_en}", fontsize=14)# 設置軸標簽plt.xlabel(x_label, fontsize=12)plt.ylabel(y_label, fontsize=12)plt.grid(alpha=0.3)plt.tight_layout()  # 緊湊布局，無需為公式預留空間# 生成包含中英文的文件名filename = f"{filename_cn}_{filename_en}_{params_str}.jpg"plt.savefig(filename, dpi=300, bbox_inches='tight')plt.close()# 1. 伯努利分布
def plot_bernoulli():x = [0, 1]p = 0.6pmf = [1 - p, p]plt.bar(x, pmf, color='skyblue', width=0.5)plt.xticks(x)plt.ylim(0, 1.1)return pp = plot_bernoulli()
save_distribution_plot(plot_bernoulli, [], f'伯努利分布 (p={p})', f'Bernoulli Distribution (p={p})','隨機變量值 (Random Variable Value)', '概率 (Probability)','伯努利分布', 'bernoulli', f'p{p}', True
)# 2. 二項分布
def plot_binomial():n, p = 10, 0.4x = np.arange(0, n + 1)pmf = stats.binom.pmf(x, n, p)plt.bar(x, pmf, color='salmon', width=0.6)plt.ylim(0, 0.35)return n, pn, p = plot_binomial()
save_distribution_plot(plot_binomial, [], f'二項分布 (n={n}, p={p})', f'Binomial Distribution (n={n}, p={p})','成功次數 (Number of Successes)', '概率 (Probability)','二項分布', 'binomial', f'n{n}_p{p}', True
)# 3. 泊松分布
def plot_poisson():lambda_p = 4x = np.arange(0, 16)pmf = stats.poisson.pmf(x, lambda_p)plt.bar(x, pmf, color='lightgreen', width=0.7)plt.ylim(0, 0.25)return lambda_plambda_p = plot_poisson()
save_distribution_plot(plot_poisson, [], f'泊松分布 (λ={lambda_p})', f'Poisson Distribution (λ={lambda_p})','事件發生次數 (Number of Occurrences)', '概率 (Probability)','泊松分布', 'poisson', f'lambda{lambda_p}', True
)# 4. 幾何分布
def plot_geometric():p = 0.3x = np.arange(1, 11)pmf = stats.geom.pmf(x, p)plt.bar(x, pmf, color='purple', width=0.6)plt.ylim(0, 0.35)return pp = plot_geometric()
save_distribution_plot(plot_geometric, [], f'幾何分布 (p={p})', f'Geometric Distribution (p={p})','首次成功前的試驗次數 (Trials Until First Success)', '概率 (Probability)','幾何分布', 'geometric', f'p{p}', True
)# 5. 負二項分布
def plot_negative_binomial():r, p = 5, 0.6x = np.arange(5, 16)pmf = stats.nbinom.pmf(x - r, r, p)plt.bar(x, pmf, color='orange', width=0.7)plt.ylim(0, 0.25)return r, pr, p = plot_negative_binomial()
save_distribution_plot(plot_negative_binomial, [], f'負二項分布 (r={r}, p={p})', f'Negative Binomial Distribution (r={r}, p={p})','第r次成功時的試驗次數 (Trials Until r-th Success)', '概率 (Probability)','負二項分布', 'negative_binomial', f'r{r}_p{p}', True
)# 6. 均勻分布
def plot_uniform():a, b = 2, 8x = np.linspace(a - 1, b + 1, 1000)pdf = stats.uniform.pdf(x, loc=a, scale=b - a)plt.plot(x, pdf, color='red')plt.fill_between(x, pdf, alpha=0.3, color='red')plt.ylim(0, 0.2)return a, ba, b = plot_uniform()
save_distribution_plot(plot_uniform, [], f'均勻分布 (a={a}, b={b})', f'Uniform Distribution (a={a}, b={b})','隨機變量值 (Random Variable Value)', '概率密度 (Probability Density)','均勻分布', 'uniform', f'a{a}_b{b}', False
)# 7. 正態分布
def plot_normal():mu, sigma = 0, 2x = np.linspace(mu - 4*sigma, mu + 4*sigma, 1000)pdf = stats.norm.pdf(x, mu, sigma)plt.plot(x, pdf, color='blue')plt.fill_between(x, pdf, alpha=0.3, color='blue')plt.ylim(0, 0.25)return mu, sigmamu, sigma = plot_normal()
save_distribution_plot(plot_normal, [], f'正態分布 (μ={mu}, σ={sigma})', f'Normal Distribution (μ={mu}, σ={sigma})','隨機變量值 (Random Variable Value)', '概率密度 (Probability Density)','正態分布', 'normal', f'mu{mu}_sigma{sigma}', False
)# 8. 指數分布
def plot_exponential():lambda_exp = 0.5x = np.linspace(0, 6, 1000)pdf = stats.expon.pdf(x, scale=1/lambda_exp)plt.plot(x, pdf, color='green')plt.fill_between(x, pdf, alpha=0.3, color='green')plt.ylim(0, 0.6)return lambda_explambda_exp = plot_exponential()
save_distribution_plot(plot_exponential, [], f'指數分布 (λ={lambda_exp})', f'Exponential Distribution (λ={lambda_exp})','時間間隔 (Time Interval)', '概率密度 (Probability Density)','指數分布', 'exponential', f'lambda{lambda_exp}', False
)# 9. 伽瑪分布
def plot_gamma():a, beta = 2, 1x = np.linspace(0, 6, 1000)pdf = stats.gamma.pdf(x, a, scale=1/beta)plt.plot(x, pdf, color='brown')plt.fill_between(x, pdf, alpha=0.3, color='brown')plt.ylim(0, 1.0)return a, betaa, beta = plot_gamma()
save_distribution_plot(plot_gamma, [], f'伽瑪分布 (a={a}, β={beta})', f'Gamma Distribution (a={a}, β={beta})','隨機變量值 (Random Variable Value)', '概率密度 (Probability Density)','伽瑪分布', 'gamma', f'a{a}_beta{beta}', False
)# 10. 卡方分布
def plot_chi2():k = 3x = np.linspace(0, 15, 1000)pdf = stats.chi2.pdf(x, k)plt.plot(x, pdf, color='cyan')plt.fill_between(x, pdf, alpha=0.3, color='cyan')plt.ylim(0, 0.7)return kk = plot_chi2()
save_distribution_plot(plot_chi2, [], f'卡方分布 (k={k})', f'Chi-squared Distribution (k={k})','隨機變量值 (Random Variable Value)', '概率密度 (Probability Density)','卡方分布', 'chi2', f'k{k}', False
)# 11. t分布
def plot_t():v = 5x = np.linspace(-5, 5, 1000)pdf = stats.t.pdf(x, v)plt.plot(x, pdf, color='magenta')plt.fill_between(x, pdf, alpha=0.3, color='magenta')plt.ylim(0, 0.4)return vv = plot_t()
save_distribution_plot(plot_t, [], f't分布 (v={v})', f't-Distribution (v={v})','隨機變量值 (Random Variable Value)', '概率密度 (Probability Density)','t分布', 't_distribution', f'v{v}', False
)# 12. F分布
def plot_f():d1, d2 = 5, 10x = np.linspace(0, 4, 1000)pdf = stats.f.pdf(x, d1, d2)plt.plot(x, pdf, color='gray')plt.fill_between(x, pdf, alpha=0.3, color='gray')plt.ylim(0, 1.0)return d1, d2d1, d2 = plot_f()
save_distribution_plot(plot_f, [], f'F分布 (d1={d1}, d2={d2})', f'F-Distribution (d1={d1}, d2={d2})','隨機變量值 (Random Variable Value)', '概率密度 (Probability Density)','F分布', 'f_distribution', f'd1{d1}_d2{d2}', False
)