專欄：Java數據結構秘籍

個人主頁：手握風云

目錄

一、位圖

1.1. 概念

1.2. 面試題

1.3. 位圖的實現

1.4. 位圖的應用

---

一、位圖

1.1. 概念

????????在數據結構中，位圖（也稱為位數組、位向量或位集）是一種緊湊的方式來表示一組布爾值（真/假、1/0）。它本質上是一個數組，其中每個元素代表一個位，該位的位置通常對應于一個標識符或索引。適用于海量數據，整數，數據無重復的場景。

1.2. 面試題

????????給40億個不重復的無符號整數，沒排過序。給一個無符號整數，如何快速判斷一個數是否在這40億個數中。

????????解法：

1. 遍歷，時間復雜度。
2. 排序+二分查找，時間復雜度。10億個byte大約是1G，10億個整數大約是4G，40億個整數大約就是16G，很明顯內存不夠

? ? ? ? 這時我們就可以使用位圖來解決上述問題。我們知道一個整數是32個比特位，那么每一個比特位就可以存儲不同的數字，0代表沒出現過，1代表出現過。那我們就可以根據一組數據的某種關系映射到里面。

? ? ? ? 如下圖所示，我們就可以以8個比特位為一組，每個數據進行/8的操作，然后將其儲存在比特位的下標里面。

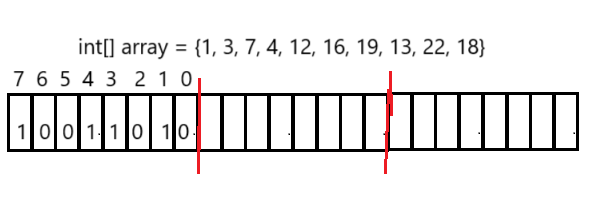
? ? ? ? 這樣的話40億個整數只需大約476MB就可以解決。

1.3. 位圖的實現

? ? ? ? 在Java的集合框架中，也有BitSet類。

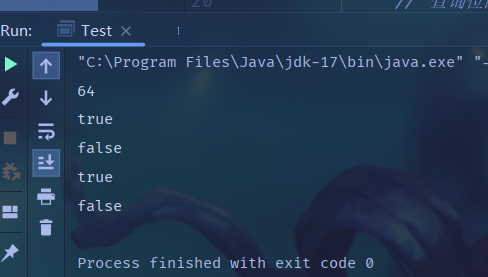
import java.util.BitSet;public class Test {public static void main(String[] args) {BitSet bitSet = new BitSet();// 設置位bitSet.set(0);bitSet.set(2);bitSet.set(4);// 獲取BitSet的大小System.out.println(bitSet.size());// 查詢位的狀態System.out.println(bitSet.get(0));System.out.println(bitSet.get(1));System.out.println(bitSet.get(2));// 清除位bitSet.clear(2);System.out.println(bitSet.get(2));}
}

public class MyBitSet {public byte[] elem;public int usedSize;public MyBitSet(byte[] elem) {this.elem = new byte[1];}/*** 有可能多給一個字節，但是無所謂* @param n 多少位*/public MyBitSet(int n) {this.elem = new byte[n / 8 + 1];}/*** 設置某一位為1，證明數據出現過* @param val 查找的數據*/public void set(int val) {}/**** @param val 輸入的數據* @return 判斷當前位是不是1*/public boolean get(int val) {return false;}/*** 將對應位置置為0* @param val 輸入的位數*/public void reSet(int val) {}// 獲取當前已經使用的位數public int getUsedSize() {return usedSize;}
}

? ? ? ? 我們先來看設置位方法。如果輸入的數據小于0，需要拋出下標越界的異常。對于輸入的數據，我們既要計算出需要對應在字節數組中的哪個字節，還要計算出在字節中的哪個bit位。之后我們還需要進行將對應的比特位下標置為1，并且不能改變其它位置的值。比如，我們要設置2位置為1，先將1左移2位，再進行按位或操作。

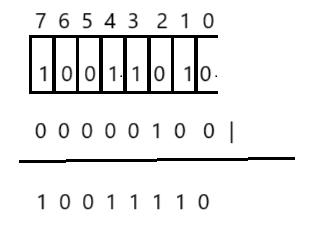
public void set(int val) {if (val < 0) {throw new IndexOutOfBoundsException();}int arrayIndex = val / 8;int bitIndex = val % 8;elem[arrayIndex] |= (1 << bitIndex);usedSize++;
}

? ? ? ? 對于get()方法，我們先左移對應的比特位，然后進行按位與的操作，如果結果不是0，說明該位置為1。

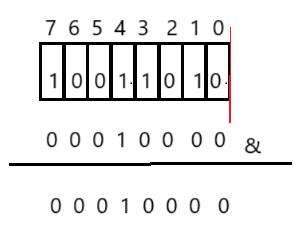
public boolean get(int val) {if (val < 0) {throw new IndexOutOfBoundsException();}int arrayIndex = val / 8;int bitIndex = val % 8;return (elem[arrayIndex] & (1 << bitIndex)) != 0;
}

? ? ? ? 對于reSet()方法，我們先假設原來這個地方為0，一進行按位與操作，就會將其變成1，所以我們先左移然后按位取反再進行安=按位與。

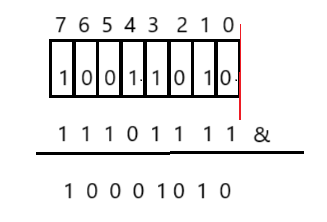
public void reSet(int val) {if (val < 0) {throw new IndexOutOfBoundsException();}int arrayIndex = val / 8;int bitIndex = val % 8;elem[arrayIndex] &= ~(1 << bitIndex);usedSize--;
}

• 測試結果

public static void main(String[] args) {int[] array = {1, 3, 7, 4, 12, 16, 19, 13, 22, 18};MyBitSet bitSet = new MyBitSet(22);for (int i = 0; i < array.length; i++) {bitSet.set(array[i]);}System.out.println(bitSet.get(7));System.out.println(bitSet.get(5));System.out.println(bitSet.get(50));
}

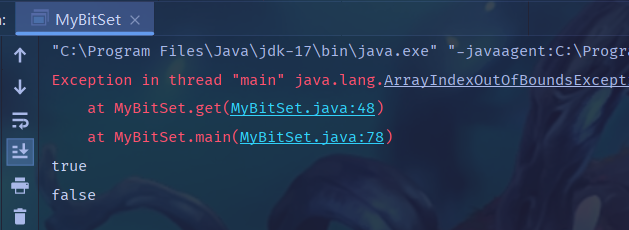
? ? ? ? 出現異常正是因為沒有進行擴容，50 / 8結果是6，就會產生越界異常。

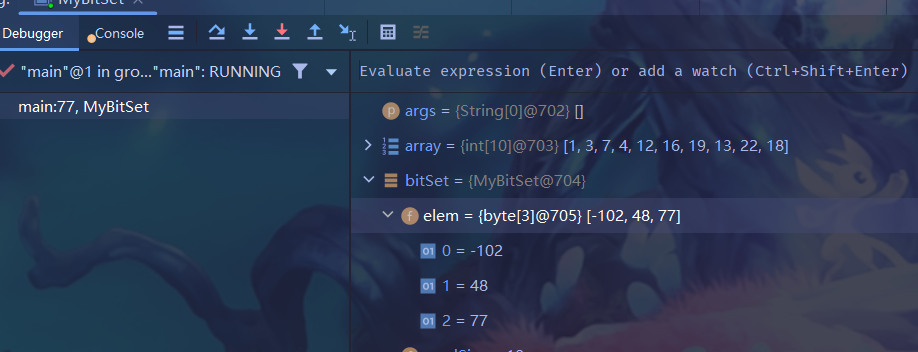
? ? ? ? 完整代碼實現：

import java.util.Arrays;public class MyBitSet {public byte[] elem;public int usedSize;public MyBitSet(byte[] elem) {this.elem = new byte[1];}/*** 有可能多給一個字節，但是無所謂* @param n 多少位*/public MyBitSet(int n) {this.elem = new byte[n / 8 + 1];}/*** 設置某一位為1，證明數據出現過* @param val 查找的數據*/public void set(int val) {if (val < 0) {throw new IndexOutOfBoundsException();}int arrayIndex = val / 8;// 擴容if (arrayIndex > elem.length - 1) {elem = Arrays.copyOf(elem, arrayIndex + 1);}int bitIndex = val % 8;elem[arrayIndex] |= (1 << bitIndex);usedSize++;}/**** @param val 輸入的數據* @return 判斷當前位是不是1*/public boolean get(int val) {if (val < 0) {throw new IndexOutOfBoundsException();}int arrayIndex = val / 8;int bitIndex = val % 8;if (arrayIndex >= elem.length) {return false;}return (elem[arrayIndex] & (1 << bitIndex)) != 0;}/*** 將對應位置置為0* @param val 輸入的位數*/public void reSet(int val) {if (val < 0) {throw new IndexOutOfBoundsException();}int arrayIndex = val / 8;int bitIndex = val % 8;elem[arrayIndex] &= ~(1 << bitIndex);usedSize--;}// 獲取當前已經使用的位數public int getUsedSize() {return usedSize;}public static void main(String[] args) {int[] array = {1, 3, 7, 4, 12, 16, 19, 13, 22, 18};MyBitSet bitSet = new MyBitSet(22);for (int i = 0; i < array.length; i++) {bitSet.set(array[i]);}System.out.println(bitSet.get(7));System.out.println(bitSet.get(5));System.out.println(bitSet.get(50));}
}

1.4. 位圖的應用

1. 高效存儲與查詢大量布爾狀態；
2. 集合運算（交集、并集、差集）；
3. 位圖排序（適合范圍已知的整數排序）
4. 去重與計數；
5. 布隆過濾器（Bloom Filter）底層實現