關聯規則挖掘2：FP-growth算法（Frequent Pattern Growth，頻繁模式增長）

一、核心思想：一個形象的比喻

二、核心思想的具體拆解

步驟一：構建FP-tree（頻繁模式樹）

步驟二：從FP-tree中挖掘頻繁項集

為什么這很高效？

三、總結

核心思想與優勢

適用場景與缺點

四、例題

給定數據

第一步：第一次掃描數據庫，找出頻繁1項集及其支持度

第二步：第二次掃描數據庫，構建FP-tree

第三步：挖掘FP-tree，尋找頻繁項集

1. 以后綴?A?開始挖掘

步驟 1: 尋找條件模式基 (Conditional Pattern Base)

步驟 2: 構建條件FP-tree (Conditional FP-tree) for?A

步驟 3: 挖掘條件FP-tree并生成頻繁項集

2. 以后綴?E?開始挖掘

步驟 1: 尋找條件模式基 for?E

步驟 2: 構建條件FP-tree for?E

步驟 3: 挖掘條件FP-tree for?E

3. 以后綴?C?開始挖掘

步驟 1: 尋找條件模式基 for?C

步驟 2: 構建條件FP-tree for?C

步驟 3: 挖掘條件FP-tree for?C

4. 以后綴?B?開始挖掘

步驟 1: 尋找條件模式基 for?B

步驟 2: 構建條件FP-tree for?B

步驟 3: 挖掘條件FP-tree for?B

第四步：匯總所有頻繁項集

最終答案

?參考：

Python數據挖掘實戰：微課版 - 9.3 FP-growth算法 - 王磊邱江濤 - 微信讀書

19.FpGrowth算法介紹_嗶哩嗶哩_bilibili
9.2 利用FP-tree挖掘頻繁項集的過程

FP-growth（Frequent Pattern Growth，頻繁模式增長）算法是用于高效挖掘數據集中頻繁項集的一種方法。它極大地改進了傳統的Apriori算法，核心目標仍然是找出所有滿足最小支持度閾值的項集。

其核心思想可以概括為：“分而治之”?和?“用空間換時間”。

一、核心思想：一個形象的比喻

想象一下，你要統計一圖書館里所有書籍的組合借閱情況（比如，同時被借閱的書籍組合）。

Apriori算法（傳統方法）：像一個笨拙的圖書管理員。他需要反復穿梭于各個書架之間，每次只關心“2本書的組合”，統計完后再找“3本書的組合”，如此反復。這個過程會產生大量的“候選組合”，并且需要反復掃描整個借閱記錄（數據庫），非常耗時。
FP-growth算法（新方法）：像一個聰明的圖書管理員。他首先花一點時間，為整個圖書館建立了一個非常精巧的索引目錄（FP-tree）。這個目錄不僅記錄了每本書被借閱的次數，還清晰地記錄了哪些書經常被一起借閱。當你想查詢任何書籍組合時，他無需再跑回書架，只需在這個濃縮的目錄里進行查找和拼接，就能快速得到結果。

這個“精巧的目錄”就是FP-growth算法的精髓。

二、核心思想的具體拆解

FP-growth算法主要分為兩個核心步驟，完美體現了其思想：

步驟一：構建FP-tree（頻繁模式樹）

這是“用空間換時間”和“數據壓縮”的體現。

第一次掃描數據庫：統計所有單項（1項集）的支持度，并丟棄那些不頻繁的項（低于最小支持度）。
排序：將剩余的頻繁項按照支持度從高到低排序。這樣做的好處是，出現頻率高的項更靠近樹的根部，使得樹的深度盡可能小，更加緊湊。
第二次掃描數據庫：開始構建FP-tree。
- 將每條事務（例如一次購物籃記錄?{牛奶，面包，啤酒}）中的項按第二步的順序排序和過濾（例如排序后為?{啤酒，面包，牛奶}）。
- 從樹的根節點開始，為這條事務創建一條分支。如果分支的前綴與已有路徑共享，則共享節點的計數加1；如果不共享，則創建新的節點。
- 同時，為了快速訪問樹中的節點，還維護了一個頭指針表，它鏈接了所有相同名稱的節點。

為什么這很巧妙？

壓縮數據庫：原始的數據庫被壓縮成了一棵FP-tree。事務數據中共享的頻繁項被合并到了同一條路徑上，大大減少了存儲空間。
信息完整：這棵樹完整地保留了項集之間的關聯和頻率信息。

步驟二：從FP-tree中挖掘頻繁項集

這是“分而治之”思想的體現。

挖掘過程是遞歸的。我們不是從整個大樹開始挖，而是從小樹枝開始。

從后綴開始：從頭指針表中支持度最低的項（即樹的枝葉末梢）開始，作為當前的后綴模式（例如?{牛奶}）。
尋找條件模式基：沿著頭指針表，找到FP-tree中所有包含此后綴的路徑。這些路徑去掉后綴后剩下的前綴部分，以及路徑上的計數，就構成了條件模式基。這相當于為“牛奶”這個項創建了一個子數據庫。
構建條件FP-tree：以這個條件模式基作為新的“數據庫”，重復步驟一的過程，構建一個只與“牛奶”相關的條件FP-tree。
遞歸挖掘：如果條件FP-tree不是空的（例如一條單路徑），則遞歸地挖掘這棵小樹。如果它是一條單路徑，則直接生成該路徑上所有節點的組合，并與后綴模式合并，即可得到所有頻繁項集（例如，從路徑?啤酒：3，面包：3?可以得到?{啤酒，面包，牛奶}，{啤酒，牛奶}，{面包，牛奶}）。
移動指針：處理完一個后綴后，就回頭指針表中移動到下一個支持度稍高的項（例如?{面包}），重復步驟2-4，直到處理完所有項。

為什么這很高效？

分治：將挖掘整個大數據集的任務，分解為挖掘多個更小的條件數據庫的任務，問題規模指數級減小。
避免候選集生成：它不需要產生大量的候選集（這是Apriori的主要瓶頸），而是通過遞歸和直接拼接來生成頻繁項集。
無重復掃描數據庫：整個過程中，原始數據庫只被掃描了兩次（構建FP-tree時）。之后的所有操作都是在內存中對這棵壓縮樹進行操作，速度極快。

三、總結

核心思想與優勢

方面	核心思想闡述	帶來的優勢
數據表示	用空間換時間：花費內存構建一個高度壓縮、信息完整的數據結構（FP-tree）。	大幅減少I/O開銷：僅需掃描數據庫兩次，后續操作均在內存中進行。
挖掘策略	分而治之：通過遞歸地構建條件模式基和條件FP-tree，將大問題分解為多個小問題。	效率極高：避免了產生海量候選集，算法復雜度通常遠低于Apriori。
搜索方法	模式增長：從后綴模式出發，通過拼接前綴路徑來直接生成頻繁模式，而非通過候選和測試。	精準高效：沒有無效的候選集生成和測試過程。

適用場景與缺點

適用場景：非常適合挖掘稠密數據集（即事務中項之間相關性較強，共享前綴多），能獲得很好的壓縮效果和性能提升。
缺點：
- 空間消耗：FP-tree及其遞歸過程中構建的條件FP-tree可能會消耗大量內存，尤其是在處理稀疏數據集或支持度閾值很低時。
- 實現復雜度：相對于Apriori，其實現更為復雜。

FP-growth算法的核心在于創新地使用樹結構來壓縮存儲數據，并基于此結構采用分而治之的策略進行高效挖掘，從而解決了Apriori算法多次掃描數據庫和產生大量候選集的兩個主要性能瓶頸。

四、例題

給定數據

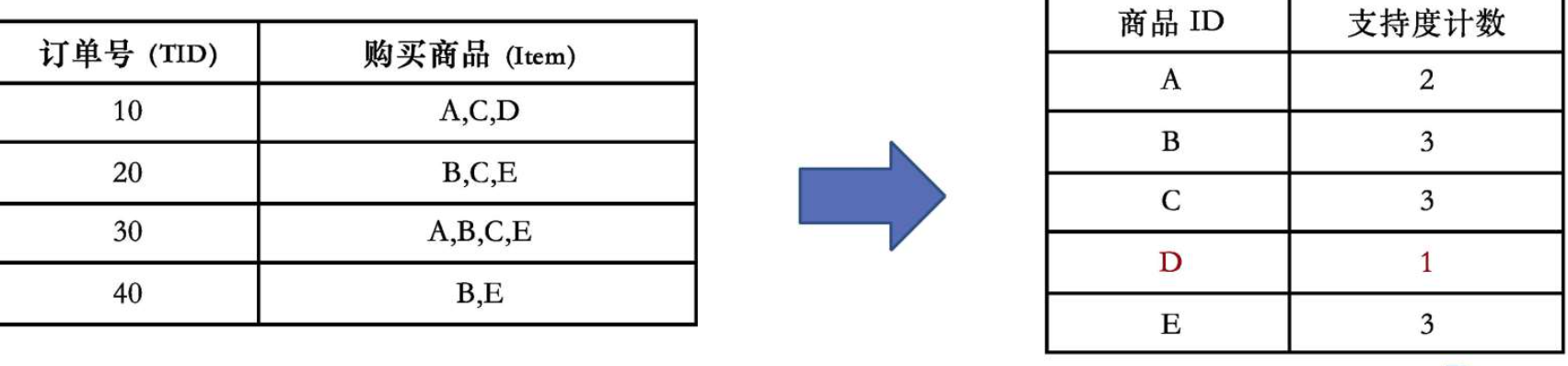
TID	Items
10	A, C, D
20	B, C, E
30	A, B, C, E
40	B, E

設定最小支持度 (min_sup)：?為了演示方便，我們設定最小支持度為?2?(即出現次數 >= 2)。

第一步：第一次掃描數據庫，找出頻繁1項集及其支持度

我們統計每個商品在所有訂單中出現的總次數。

A: 出現在T10, T30 → 計數 = 2
B: 出現在T20, T30, T40 → 計數 = 3
C: 出現在T10, T20, T30 → 計數 = 3
D: 出現在T10 → 計數 = 1?(小于min_sup=2，丟棄)
E: 出現在T20, T30, T40 → 計數 = 3

篩選并排序后的頻繁1項集（按支持度降序排列）：

商品	支持度
B	3
C	3
E	3
A	2

順序為: B, C, E, A?(支持度相同時，順序可任意，但必須固定)

第二步：第二次掃描數據庫，構建FP-tree

我們為每條事務（訂單）中的商品按照上一步確定的順序（B, C, E, A）進行排序，并過濾掉非頻繁項（此例中為D）。

T10:?A, C, D?→ 過濾D →?A, C?→ 按順序排序 →?C, A?(因為C的支持度3 > A的支持度2)
T20:?B, C, E?→ 按順序排序 →?B, C, E
T30:?A, B, C, E?→ 按順序排序 →?B, C, E, A
T40:?B, E?→ 按順序排序 →?B, E

現在，我們開始構建FP-tree。Root是根節點，為空。

插入 T10:?C, A

從Root開始，創建子節點?C:1。
從?C:1?開始，創建子節點?A:1。

插入 T20:?B, C, E

從Root開始，沒有?B?子節點，創建?B:1。
從?B:1?開始，創建子節點?C:1。
從?C:1?開始，創建子節點?E:1。

插入 T30:?B, C, E, A

從Root開始，已有?B?子節點，將其計數加1 →?B:2。
從?B:2?開始，已有?C?子節點，將其計數加1 →?C:2。
從?C:2?開始，已有?E?子節點，將其計數加1 →?E:2。
從?E:2?開始，沒有?A?子節點，創建新的子節點?A:1。

插入 T40:?B, E

從Root開始，已有?B?子節點，將其計數加1 →?B:3。
從?B:3?開始，沒有?E?子節點（B的子節點目前是?C:2，不是?E），因此創建一個新的子節點?E:1。

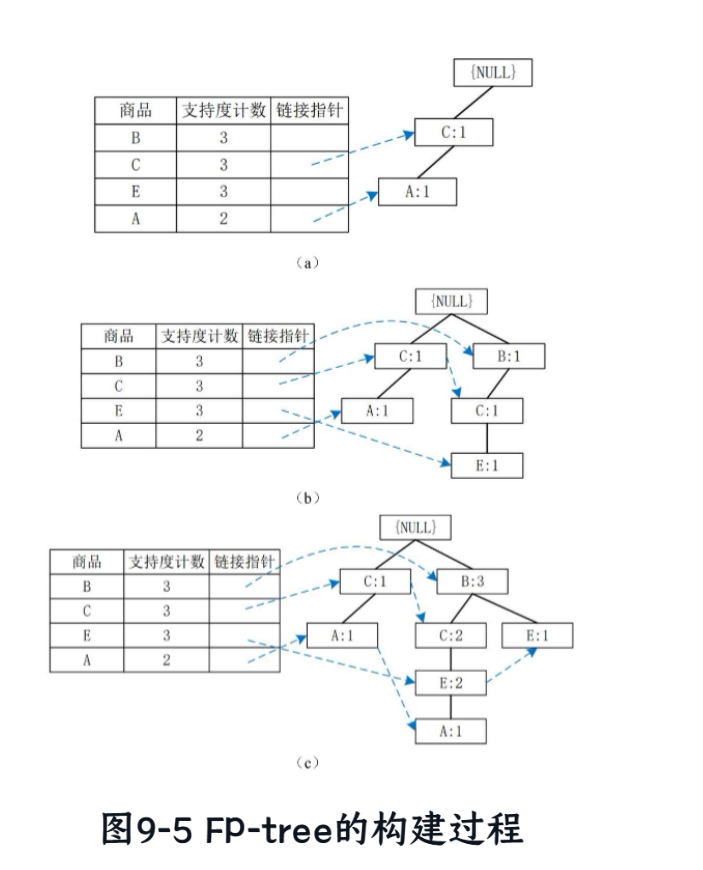
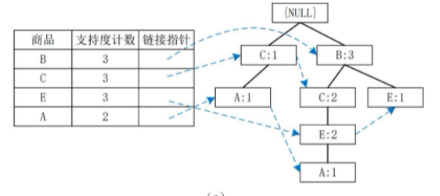
最終構建的FP-tree如下圖所示：
(為了清晰，我們同時維護一個頭指針表，將相同名稱的節點鏈接起來)

        Root/    \B:3    C:1/   \      \E:1   C:2    A:1\E:2\A:1

頭指針表 (Header Table):

B?→ 鏈接到?(B:3)
C?→ 鏈接到?(C:1)?->?(C:2)
E?→ 鏈接到?(E:1)?->?(E:2)
A?→ 鏈接到?(A:1)?->?(A:1)

第三步：挖掘FP-tree，尋找頻繁項集

我們從頭指針表底部的支持度最低的項開始（即A），然后向上是E，C，最后是B。

1. 以后綴?`A`?開始挖掘

步驟 1: 尋找條件模式基 (Conditional Pattern Base)
- 在FP-tree中，找到所有以?A?結尾的路徑。
- 路徑1:?C:1?->?A:1?(來自T10?C, A)
  - 前綴路徑:?C:1
- 路徑2:?B:3?->?C:2?->?E:2?->?A:1?(來自T30?B, C, E, A)
  - 前綴路徑:?B:3, C:2, E:2
- A?的條件模式基是?{C:1}?和?{B:3, C:2, E:2}。
步驟 2: 構建條件FP-tree (Conditional FP-tree) for?A
- 以條件模式基作為新的事務數據庫。
- 事務1:?C?(計數為1)
- 事務2:?B, C, E?(計數為路徑上的最小值，即?A?的計數1？這里需要修正：計數應取路徑末尾目標節點A的計數，即每條前綴路徑的計數應等于該路徑上A節點的計數)
  - 修正：路徑?C:1 -> A:1，A的計數是1，所以前綴路徑?C?的計數是1。
  - 路徑?B:3, C:2, E:2 -> A:1，A的計數是1，所以前綴路徑?B, C, E?的計數是1。
- 現在統計這個新“數據庫”中項的支持度：
  - C: 1 (來自事務1) + 1 (來自事務2) = 2
  - B: 1 (來自事務2) = 1?(< min_sup=2，丟棄)
  - E: 1 (來自事務2) = 1?(< min_sup=2，丟棄)
- 頻繁項只有?C:2。
- 條件FP-tree for?A?是一條單路徑?C:2。
步驟 3: 挖掘條件FP-tree并生成頻繁項集
- 條件FP-tree是單路徑?C:2。
- 該路徑上所有項的非空組合與后綴?A?合并，即可得到頻繁項集：
  - {C}?+?{A}?=?{C, A}?(支持度 = min(2, ...) ，通常取條件模式基中計數的匯總，這里?{C,A}?的支持度是?C:1路徑的1 +?B,C,E:1路徑的1？?更準確的做法：項集的支持度是其條件FP-tree根節點的計數？這里我們最終看原始計數)
  - 從原始數據看，{C, A}?出現在T10和T30，支持度確實是2。
- 所以，以后綴?A?挖掘出的頻繁項集是:?{C, A}?(支持度2)。

結論：包含A的頻繁項集為?{A}?(2),?{C,A}?(2)。?({A}?本身是頻繁1項集)

（應該是：由于項目{B},{E}不滿足最小支持度計數閾值，所以被刪除。）

2. 以后綴?`E`?開始挖掘

步驟 1: 尋找條件模式基 for?E
- 在FP-tree中，找到所有以?E?結尾的路徑。
- 路徑1:?B:3?->?C:2?->?E:2?(來自T20和T30?B,C,E)
  - 前綴路徑:?B:3, C:2?(計數為?E?的計數2)
- 路徑2:?B:3?->?E:1?(來自T40?B,E)
  - 前綴路徑:?B:3?(計數為?E?的計數1)
- E?的條件模式基是?{B:3, C:2}?(計數2) 和?{B:3}?(計數1)。
步驟 2: 構建條件FP-tree for?E
- 事務1:?B, C?(計數2)
- 事務2:?B?(計數1)
- 統計新數據庫支持度：
  - B: 2 + 1 = 3 (>=2，保留)
  - C: 2 (>=2，保留)
- 按支持度降序排序：B,?C。
- 構建條件FP-tree：
  - 插入?B, C?(計數2): Root ->?B:2?->?C:2
  - 插入?B?(計數1): Root ->?B:2?(計數+1=3)
- 最終的條件FP-tree for?E:
```
Root|B:3|C:2
```
步驟 3: 挖掘條件FP-tree for?E————（看不懂？）末尾有解釋
- 條件FP-tree不是空樹也不是單路徑，需要遞歸挖掘。
- 首先，以后綴?{C, E}?開始挖掘?(從條件FP-tree的底部項C開始)
  - 尋找?{C, E}?的條件模式基: 在?E?的條件FP-tree中，找到所有以?C?結尾的路徑。路徑：B:3 -> C:2。
    - 前綴路徑:?B:3?(計數為?C?的計數2)
  - 構建?{C, E}?的條件FP-tree:
    - 事務:?B?(計數2)
    - 統計支持度：B:2 (>=2，保留)
    - 條件FP-tree for?{C,E}?是單路徑?B:2。
  - 挖掘?{C,E}?的條件FP-tree:
    - 生成組合:?{B}?+?{C,E}?=?{B, C, E}?(支持度2？原始數據中出現在T20和T30，支持度2)
  - 所以，包含?{C,E}?的頻繁項集:?{C,E},?{B,C,E}。
    - {C,E}?的支持度：從其條件模式基?B:3(計數2) 可以看出計數為2。原始數據中出現在T20和T30，支持度2。
- 然后，處理后綴?{E}?本身：條件FP-tree中有?B:3，所以?{B, E}?是頻繁的。
- 最終，包含?E?的頻繁項集:
  - {E}?(3)
  - {B, E}?(3) (來自條件FP-tree中的?B:3)
  - {C, E}?(2) (來自上面的挖掘)
  - {B, C, E}?(2) (來自上面的挖掘)

3. 以后綴?`C`?開始挖掘

步驟 1: 尋找條件模式基 for?C
- 在FP-tree中，找到所有以?C?結尾的路徑。
- 路徑1:?B:3?->?C:2?(來自T20和T30?B,C,...)
  - 前綴路徑:?B:3?(計數為?C?的計數2)
- 路徑2:?Root?->?C:1?(來自T10?C,...)
  - 前綴路徑:?{}?(空，計數為?C?的計數1)
- C?的條件模式基是?{B:3}?(計數2) 和?{}?(計數1)。
步驟 2: 構建條件FP-tree for?C
- 事務1:?B?(計數2)
- 事務2:?{}?(空集，計數1) //空集無法形成項集，忽略
- 統計支持度：B:2 (>=2，保留)
- 條件FP-tree for?C?是單路徑?B:2。
步驟 3: 挖掘條件FP-tree for?C
- 條件FP-tree是單路徑?B:2。
- 生成組合:?{B}?+?{C}?=?{B, C}?(支持度2)
- 所以，包含?C?的頻繁項集:
  - {C}?(3)
  - {B, C}?(2)

4. 以后綴?`B`?開始挖掘

步驟 1: 尋找條件模式基 for?B
- 在FP-tree中，找到所有以?B?結尾的路徑。B?是直接掛在Root下的。
- 路徑:?Root?->?B:3
  - 前綴路徑:?{}?(空，計數為?B?的計數3)
- B?的條件模式基是空。
步驟 2: 構建條件FP-tree for?B
- 條件模式基是空，因此條件FP-tree為空。
步驟 3: 挖掘條件FP-tree for?B
- 無法生成新的頻繁項集。
- 包含?B?的頻繁項集只有它自己:?{B}?(3)。

第四步：匯總所有頻繁項集

將所有步驟中找到的頻繁項集匯總，并去重（{A},?{B},?{C},?{E}?在第一步已得到）。

頻繁1項集 (Frequent 1-itemsets):

{A}: 2
{B}: 3
{C}: 3
{E}: 3

頻繁2項集 (Frequent 2-itemsets):

{C, A}: 2
{B, E}: 3
{C, E}: 2
{B, C}: 2

頻繁3項集 (Frequent 3-itemsets):

{B, C, E}: 2

頻繁4項集 (Frequent 4-itemsets):

至此，我們使用FP-growth算法完整地找出了給定數據集中的所有頻繁項集。整個過程的核心在于構建FP-tree并通過遞歸挖掘條件模式基來避免生成大量的候選集。

最終答案

Python數據挖掘實戰：微課版 - 9.3 FP-growth算法 - 王磊邱江濤 - 微信讀書

細節補充

我們現在的任務是從?E的條件FP-tree?里挖寶貝。這棵樹長這樣：

(Root)|
(B:3)|
(C:2)

目標：找到所有帶?E?的寶貝組合（比如?{B,E},?{C,E},?{B,C,E}）。

第一步：看樹，直接拿到第一個寶貝

樹上寫著?B:3。
意思是：B?和?E?一起出現了 3 次。
??所以，我們找到了第一個寶貝：{B, E}

第二步：處理樹上的下一個點?`C`

樹上還有一個?C:2，掛在?B?下面。我們不能直接用它，需要“放大鏡”看仔細。

為什么要為?{C,E}?再建一棵樹？
答：為了搞清楚?C?是和誰一起出現的，這樣才能拼出更大的寶貝。

怎么做？3個小步：

找?C?的路徑：在?E?的樹里，找到通到?C?的路。只有一條：B -> C。
看這條路的意思：這條路?B -> C?計數是2。
- 翻譯：B、C、E?這三個家伙一起出現了 2 次。
建新樹：我們就為?C?和?E?這個組合，建一棵超小的新樹，只記錄和它倆一起玩的人。
- 這棵新樹只有：(B:2)
- 意思：和?C、E?一起玩的，只有?B，而且玩了2次。

第三步：挖這棵超小的新樹

新樹?(B:2)?非常簡單，一眼就能看穿。

它告訴我們兩件事：
1. ??{C, E}?這個組合自己出現了 2 次。（因為?B?出現2次的前提是?C?和?E?肯定也在）
2. ??{B, C, E}?這個更大的組合出現了 2 次。（就是?B?自己加上?C?和?E）

最終我們找到了所有帶?`E`?的寶貝：

從?E?的樹本身：{B, E}?(3次)

從為?{C,E}?建的小樹里：{C, E}?(2次)，{B, C, E}?(2次)

(再加上最開始就知道的?{E}?自己)

FP-growth算法經典面試題

1. 請簡要說明FP-growth算法的核心思想是什么？

高分回答：
“FP-growth算法的核心思想是‘分而治之’和‘用空間換時間’。它通過兩次掃描數據庫，構建一個高度壓縮的數據結構——FP樹(Frequent Pattern Tree)，將原始數據完整的頻次信息壓縮存儲在其中。后續的挖掘過程不再需要反復訪問原始數據庫，而是通過遞歸地在FP樹上構建條件模式基和條件FP樹來挖掘全部的頻繁項集。這種方法完美避免了Apriori算法中耗時的候選集生成與測試過程。”

關鍵詞：?分而治之、空間換時間、FP樹、兩次掃描、條件模式基、遞歸挖掘、避免候選集生成。

2. 和Apriori算法相比，FP-growth有什么優缺點？

高分回答：
“優點是效率非常高。主要體現在兩方面：第一，它通常只需要掃描兩次數據庫，而Apriori需要掃描K+1次（K為最長頻繁項集長度），I/O開銷大大減少。第二，它不產生候選集，徹底避免了Apriori中候選集數量爆炸的問題。

缺點主要是空間消耗可能較大。FP-tree及其遞歸構建的條件FP-tree需要存儲在內存中，當數據集非常稀疏或最小支持度設置得很低時，樹的規模可能會很大，對內存是一個考驗。”

背誦模板：

優點：快。?掃描次數少（2次 vs. K+1次），無候選集。
缺點：可能占內存。?樹結構在密集數據下壓縮性好，但稀疏數據下可能內存消耗大。

3. 解釋一下什么是“條件模式基”(Conditional Pattern Base)？

高分回答：
“條件模式基是FP-growth算法遞歸挖掘過程中的一個核心概念。當我們要挖掘以某個項（比如項X）為后綴的所有頻繁項集時，我們需要在FP樹中找到所有包含X的路徑。這些路徑中，去掉后綴項X之后的前綴部分，以及路徑的計數信息，就共同構成了項X的條件模式基。它本質上是一個子數據庫，記錄了所有與X頻繁共現的項及其頻次，是構建更小子樹（條件FP-tree）的基礎。”

關鍵詞：?包含X的路徑、去掉X后的前綴、子數據庫、構建條件FP-tree的基礎。

4. FP-growth算法在什么情況下效率會下降？

高分回答：
“主要在兩種情況下效率會相對下降：

數據集非常稀疏時：這意味著事務中物品的共同前綴很少，導致構建出的FP-tree分支很多，壓縮效果不佳，樹會變得又寬又淺，占用大量內存，遞歸挖掘的效率也會降低。
最小支持度閾值設置得非常低時：這會導致大量非頻繁的項變成頻繁項，使得FP-tree的規模變得非常大，同樣會消耗大量內存和計算資源。”

關鍵詞：?數據稀疏、支持度閾值低、樹結構龐大、內存消耗大。

5. (可選) 能畫一下FP-tree的基本結構嗎？

如果問到，你可以畫一個簡單的示意圖并解釋：

        Root/  \B:3   C:1/   \     \C:2   E:1    A:1\E:2\A:1

解釋：?“從上到下表示項的先后順序，節點上的數字是計數。從根節點到任意一個節點就形成一條路徑，代表一個項集的出現模式。比如?B:3 -> C:2 -> E:2?這條路徑，表示項集?{B, C, E}?出現了2次。”

面試實戰技巧

先總后分：先一句話總結核心思想，再應要求展開細節。
對比突出：談到FP-growth，必提Apriori，用對比凸顯你的理解深度。
揚長避短：問優缺點時，先說優點，再“誠實”地提到缺點，并說明在什么情況下缺點會成為問題。
自信背誦：把這些答案背熟，面試時就能脫口而出，顯得非常熟練。