GFSS General Few-Shot Segmentation

• 任務實現方式與zero-shot有所不同
• 本篇論文只涉及同一個模態(圖像)，訓練過程中，novel class有幾個圖像提供，提供k個就稱之為k-shot。
• 先從圖像中提取class prototype，然后這個原型向量作為查詢，與圖像的patch嵌入計算相似度，然后得到最后的掩碼矩陣。
  

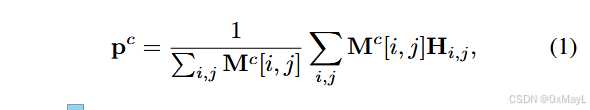
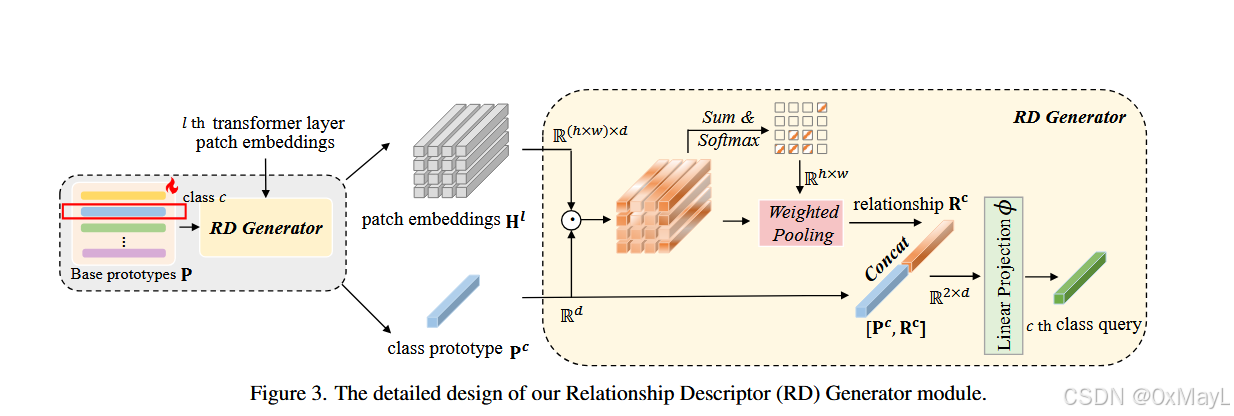
RD

• 先對patch嵌入和原型作逐元素乘法，然后賦予其特定權重。權重就是二者的相似度分數。
  

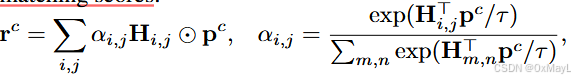
• 從VIT中提取多個patch嵌入，拼接在一起，經過線性層作為key，value。

• 拼接多個VIT layer的RD和類別原型向量，經過線性層作為query。
  

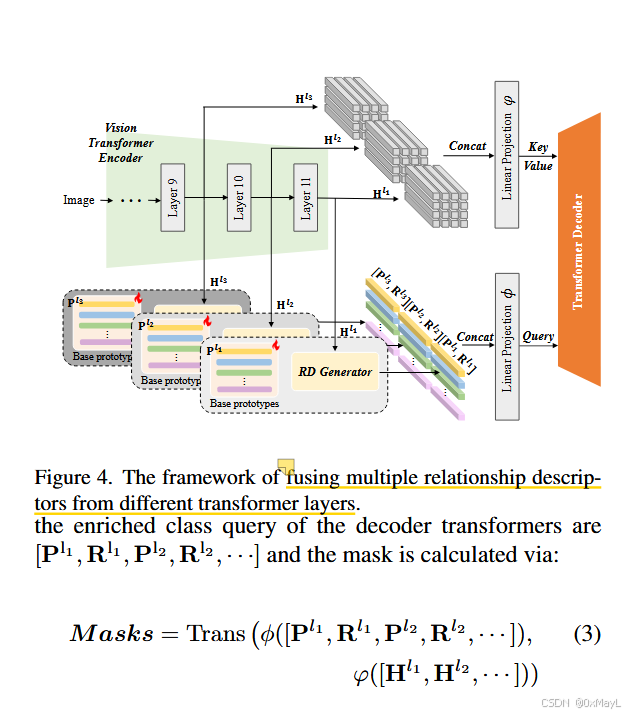
局限

依賴ViT單模態能力、計算成本高、對小樣本噪聲敏感。