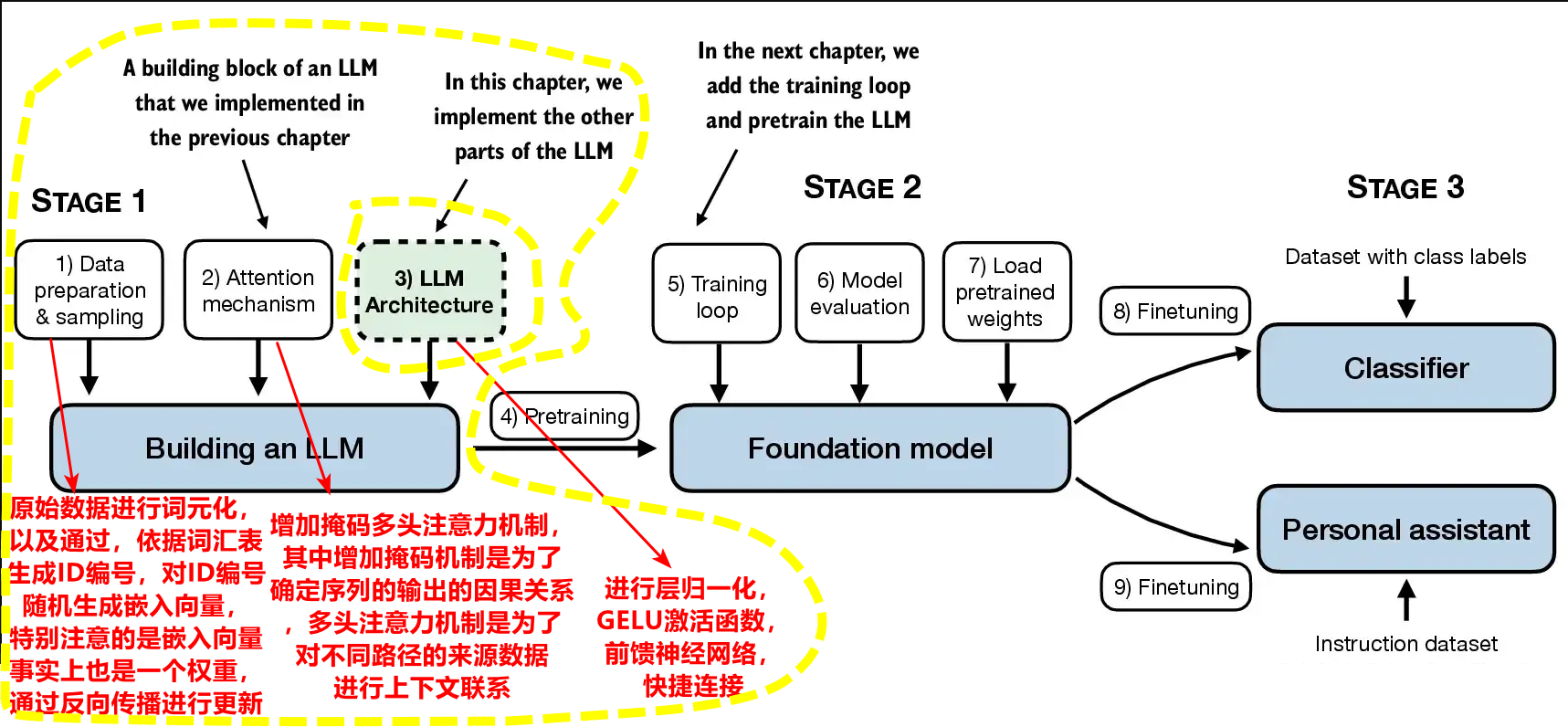
1.數據預處理：原始數據進行詞元化，以及通過，依據詞匯表生成ID編號，對ID編號隨機生成嵌入向量，特別注意的是嵌入向量事實上也是一個權重，通過反向傳播進行更新。

2.掩碼多頭注意力機制：增加掩碼多頭注意力機制，其中增加掩碼機制是為了確定序列的輸出的因果關系，多頭注意力機制是為了對不同路徑的來源數據進行上下文聯系。

3.LLM架構transform塊：進行層歸一化，GELU激活函數，前饋神經網絡，快捷連接。

1.大語言模型整體架構

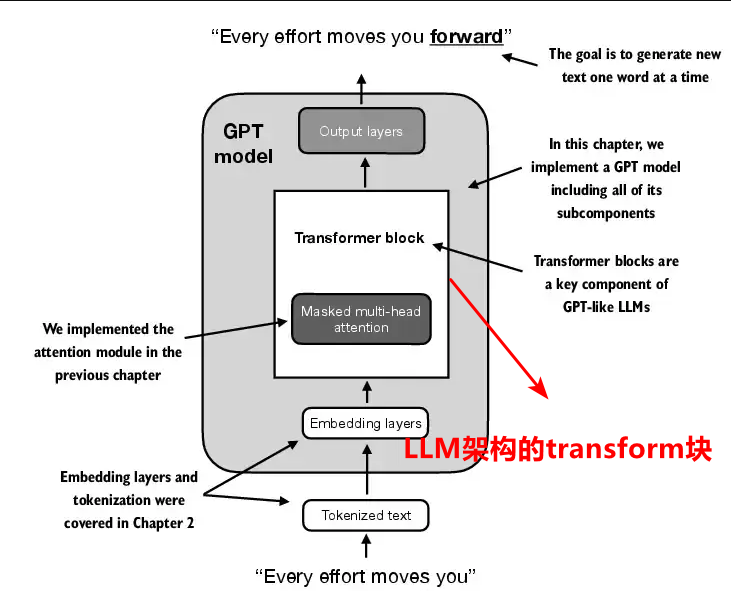
數據預處理，掩碼多頭注意力機制已經學過了，接下來進行最重要的LLM架構的transform塊的學習。
#1 Transform塊總體概述
整個transform塊包含以下內容，層歸一化，GELU激活函數，前饋神經網絡，快捷連接等等。

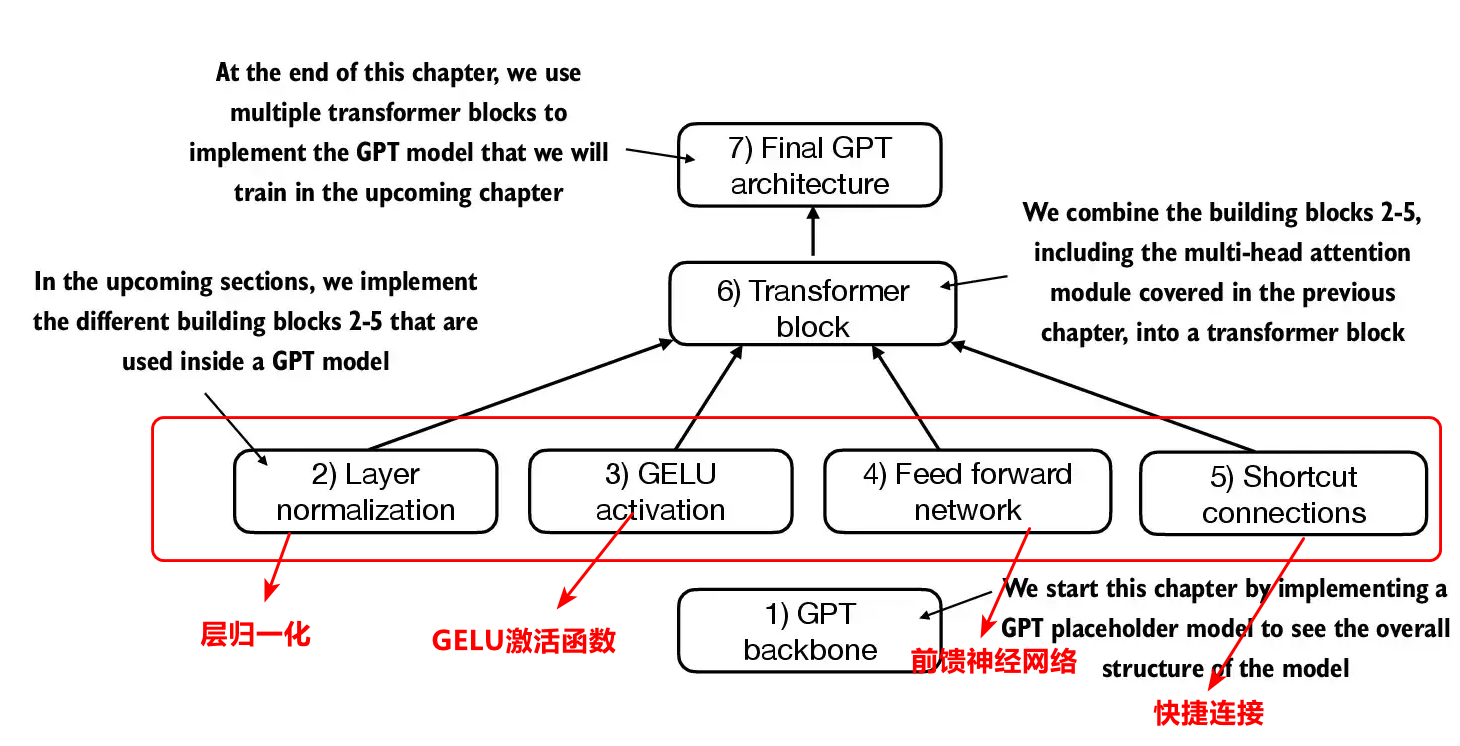
2 大語言的Transformer模塊

2.1 層歸一化

層歸一化是為了調整神經網絡的輸出，讓其均值為0，方差為1。目的是為了神經網絡更加穩定。具體做法是依據以下的數學公式，對emb_dim維度上進行$\mu =\frac{x?\mu }{\sigma }$，最終能夠對該維度嵌入向量進行歸一化，最后再加上動態可訓練參數縮放和平移。

#%% 層歸一化
import torch #導入torch包 類似于一個目錄，包含了__init__.py以及其他模塊的py文件或者其他子包
import torch.nn as nn # 導入torch包中的nn模塊 一個模塊就是一個.py文件，一個py文件下有函數以及類
torch.manual_seed(123) #固定隨機種子
batch_example = torch.randn(2,5) #隨機生成兩行五列的張量，然后每行是均值為0，方差為1的正態分布
print("batch_example,隨機生成的輸入為:",batch_example)
layer = nn.Sequential(nn.Linear(5,6),nn.ReLU()) # 容器類裝有神經網絡類，并通過序列連接，輸入連輸出，輸出也是一個神經網絡模塊
out = layer(batch_example)
print("自定義的神經網絡結構的輸出為：",out)
mean = out.mean(dim=-1,keepdim=True) #按照列的方向進行求均值，同時保持維度不變
var = out.var(dim=-1,keepdim=True) #按照行的方向進行求均值，同時保持維度不變
print("未歸一化的輸出的均值為：",mean,"未歸一化的輸出的方差為：",var)
#接下來進行歸一化
out_norm = (out- mean)/torch.sqrt(var)
torch.set_printoptions(sci_mode=False)
print("歸一化后的均值為：",out_norm.mean(dim=-1,keepdim=True))
print("歸一化后的方差為：",out_norm.var(dim=-1,keepdim=True))

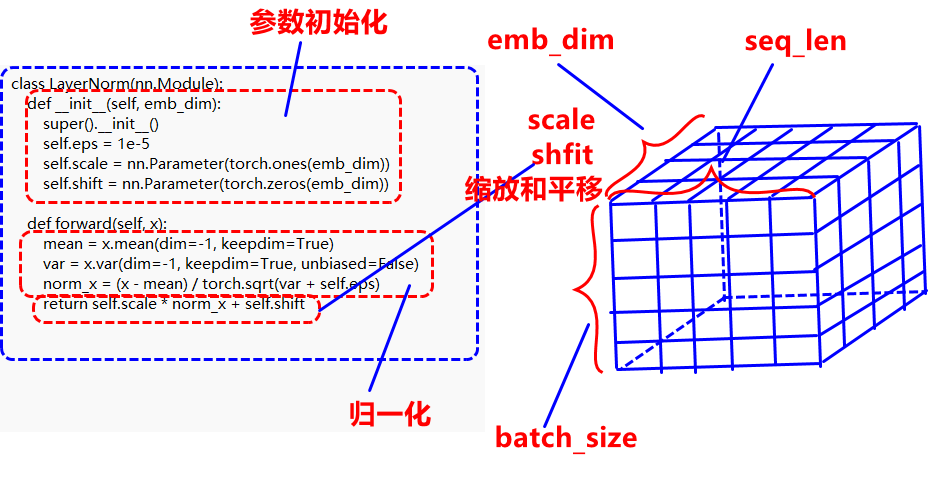
將上述歸一化代碼進行整合在一個類中：

class LayerNorm(nn.Module):def __init__(self, emb_dim):super().__init__()self.eps = 1e-5self.scale = nn.Parameter(torch.ones(emb_dim))self.shift = nn.Parameter(torch.zeros(emb_dim))def forward(self, x):mean = x.mean(dim=-1, keepdim=True)var = x.var(dim=-1, keepdim=True, unbiased=False)norm_x = (x - mean) / torch.sqrt(var + self.eps)return self.scale * norm_x + self.shift

最后測試用例：

#%% 歸一化測試用例
import torch #導入torch包 類似于一個目錄，包含了__init__.py以及其他模塊的py文件或者其他子包
import torch.nn as nn # 導入torch包中的nn模塊 一個模塊就是一個.py文件，一個py文件下有函數以及類
torch.manual_seed(123) #固定隨機種子
batch_example = torch.randn(2,5) #隨機生成兩行五列的張量，然后每行是均值為0，方差為1的正態分布
print("batch_example,隨機生成的輸入為:",batch_example)
class LayerNorm(nn.Module):def __init__(self, emb_dim):super().__init__()self.eps = 1e-5self.scale = nn.Parameter(torch.ones(emb_dim))self.shift = nn.Parameter(torch.zeros(emb_dim))def forward(self, x):mean = x.mean(dim=-1, keepdim=True)var = x.var(dim=-1, keepdim=True, unbiased=False)norm_x = (x - mean) / torch.sqrt(var + self.eps)return self.scale * norm_x + self.shift
ln = LayerNorm(emb_dim=5)
out_ln = ln(batch_example)
mean = out_ln.mean(dim=-1, keepdim=True)
var = out_ln.var(dim=-1, unbiased=False, keepdim=True)print("Mean:\n", mean)
print("Variance:\n", var)

2.2 GELU激活函數

精確的定義$GELU(x)=x??(x)$,其中$?(x)$是標準高斯分布的累積分布函數，但是在實際操作中，我們會使用一種計算量較小的近似實現，可通過曲線擬合的方法近似得到，GELU(x)≈0.5?x?{1+tanh?[π2?(x+0.044715?x3)]}GELU(x) \approx 0.5 \cdot x \cdot \{1+\tanh[\sqrt{\frac{\pi}{2}} \cdot (x+0.044715 \cdot x^{3})]\}GELU(x)≈0.5?x?{1+tanh[2π???(x+0.044715?x3)]}

#%% GELU激活函數的前饋神經網絡
#GELU激活類
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
class GELU(nn.Module):def __init__(self):# 參數初始化super().__init__()def forward(self,x): #輸入與輸出return 0.5*x*(1+torch.tanh((torch.sqrt(torch.tensor(2/torch.pi)))*(x+0.044715 * torch.power(x,3))))
# GELU激活類與ReLU激活類的對比
gelu,relu = GELU(),nn.ReLU() #神經網絡初始化
x = torch.linspace(-3,3,100)#生成-3到3之間的100個數
y_gelu = GELU(x)#前向傳播
y_relu= nn.ReLU(x)#前向傳播
plt.figure(figsize=(8,3))
for i,(label,y) in enumerate(zip(["ReLU","GELU"],[y_relu,y_gelu]),1):plt.subplot(1,2,i)plt.plot(x,y)plt.title(f"{label} activation function")plt.xlabel("x")plt.ylabel("{label}(x)")plt.grid(True)
plt.tight_layout()
plt.show()

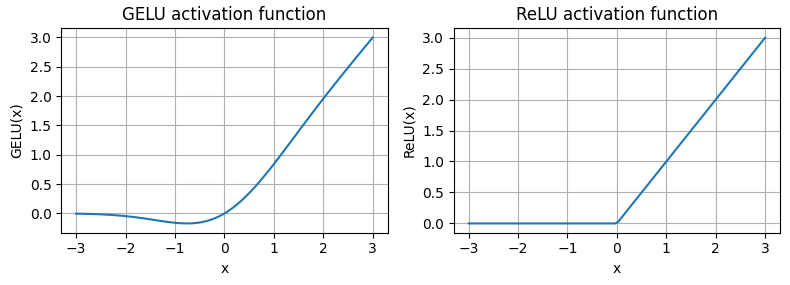
RELU激活函數存在兩個問題，第一個問題是當x=0的梯度不存在，第二個問題，輸入小于零的輸出部分直接被置為0，沒有后續神經元的運算。從GELU激活函數與ReLU激活函數對比圖可以看出，GELU在小于零部分梯度存在，同時在輸入小于0的部分，輸出接近于0，并沒有置零，還能參與后續的運算。

2.3 前饋神經網絡

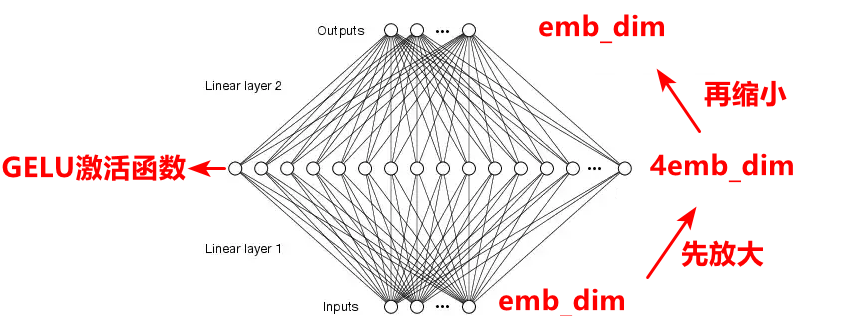
前饋神經網絡先放大輸入的節點數，經過GELU激活函數，然后再縮小節點數到與原來的輸入的節點數相同，通過這樣一個過程，相當于去粗取精。

#%% 前饋神經網絡
import torch
import torch.nn as nn
class FeedForward(nn.Module):#通過大模型進行層數的放大，然后再將層數縮小def __init__(self,cfg):#參數初始化，以及神經網絡結構的定義super().__init__()self.layers = nn.Sequential(nn.Linear(cfg['emb_dim'],4*cfg['emb_dim']),nn.GELU(),nn.Linear(4*cfg['emb_dim'],cfg['emb_dim']))#用容器來裝載神經網絡結構def forward(self,x):#定義輸入與輸出的關系return self.layers(x)

2.4 快捷連接

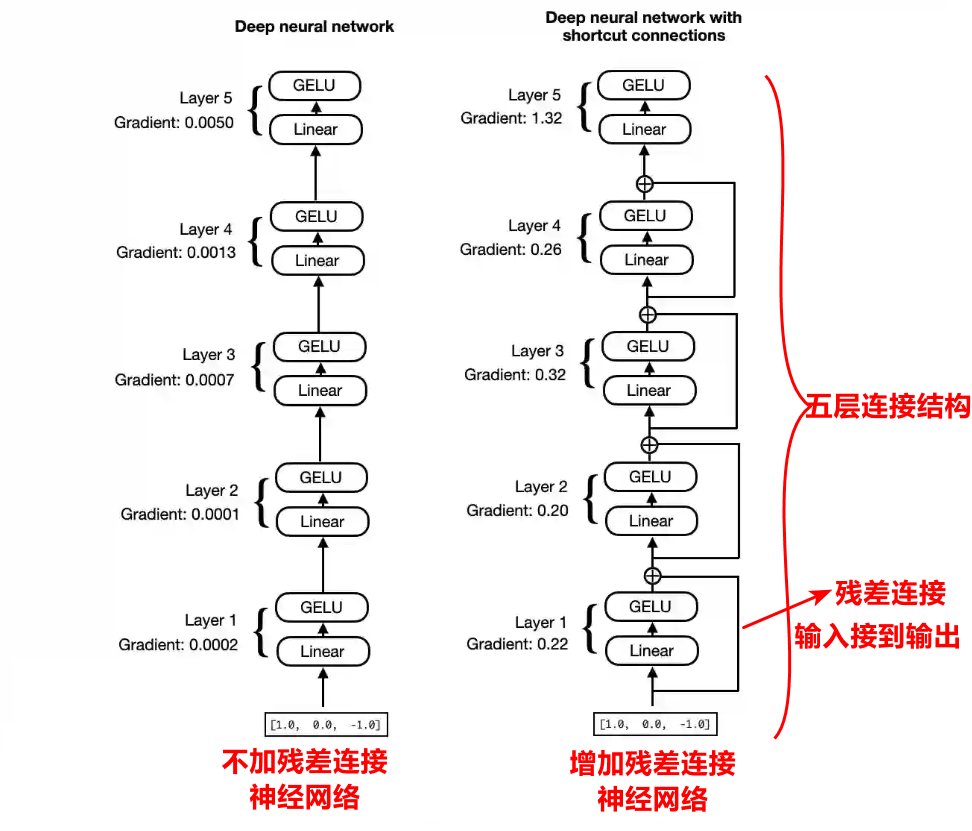
殘差連接實際上就是建立一個輸入直接連接到輸出，這樣的話，下一層輸入就變成了上一層的輸出和上一層的輸入的疊加。建立殘差連接能夠緩解梯度消失問題。

#%% 殘差連接 shortcut
import torch
import torch.nn as nn
class ShortCutNn(nn.Module):def __init__(self,layer_sizes,use_shortcut):#參數初始化以及網絡結構的定義super().__init__()self.use_shortcut = use_shortcutself.layers = nn.ModuleList([nn.Sequential(nn.Linear(layer_sizes[0],layer_sizes[1]),nn.GELU())#定義網絡列表,nn.Sequential(nn.Linear(layer_sizes[1],layer_sizes[2]),nn.GELU()),nn.Sequential(nn.Linear(layer_sizes[2],layer_sizes[3]),nn.GELU()),nn.Sequential(nn.Linear(layer_sizes[3],layer_sizes[4]),nn.GELU()),nn.Sequential(nn.Linear(layer_sizes[4],layer_sizes[5]),nn.GELU())])def forward(self,x):for layer in self.layers:layer_out = layer(x)if self.use_shortcut and x.shape == layer_out.shape:x = x + layer_outelse:x = layer_outreturn x

3 附錄

3.1 anaconda+python環境搭建

接下來進行代碼準備，首先下載所有的requirements.txt中的所有依賴庫，本次實驗是在conda+pycharm環境下，推薦大家在conda+pycharm下進行：
首先創建conda下的環境LLM

conda create --p D:/.conda/envs/LLM 

然后激活conda下的LLM環境：

conda activate  D:/.conda/envs/LLM 
conda install requirements.txt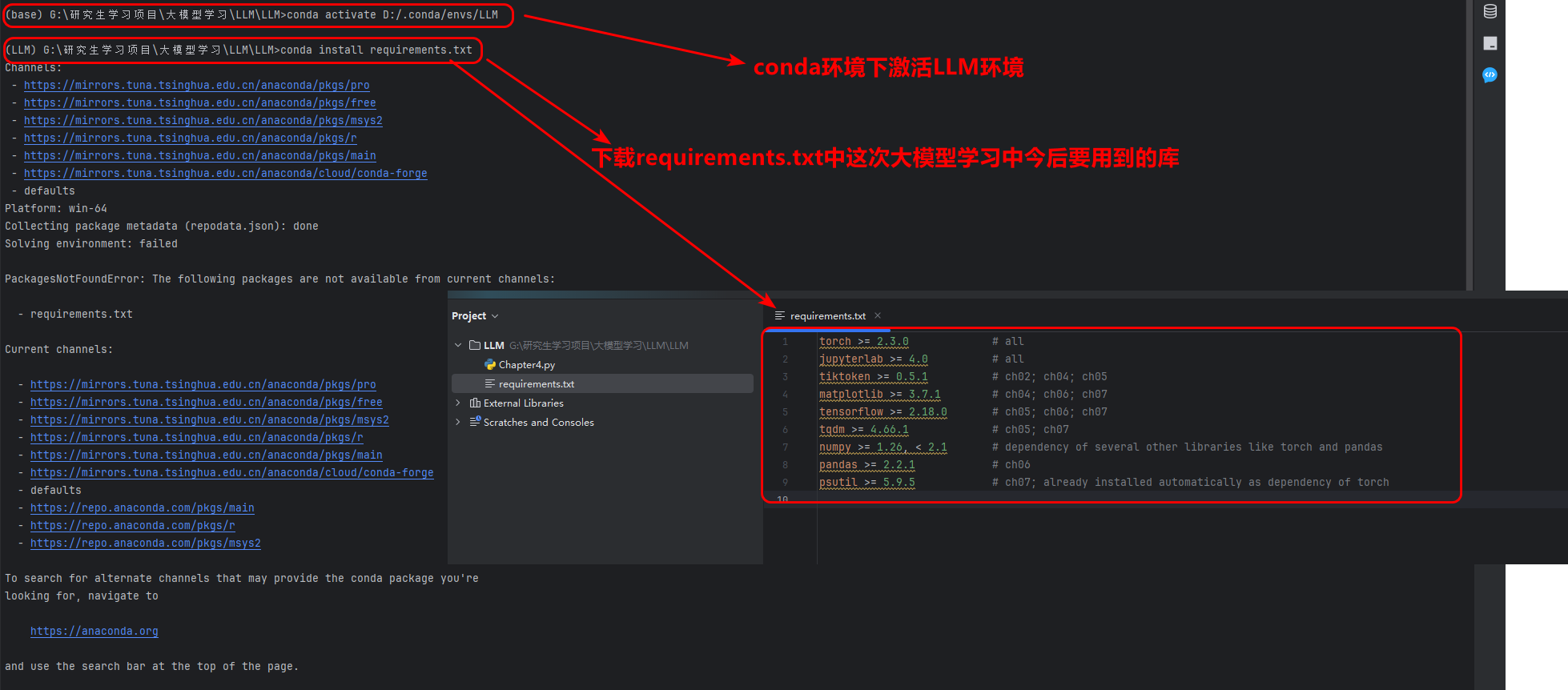

#%% 1 初始化信息查看
from importlib.metadata import version
print("matplotlib version:", version("matplotlib"))
print("torch version:", version("torch"))
print("tiktoken version:", version("tiktoken"))
#%% 2 配置GPT模型參數配置
GPT_CONFIG_124M = {"vocab_size": 50257,    # Vocabulary size 表示會被BPE分詞器使用的由50257個單詞的詞匯表"context_length": 1024, # Context length  能夠處理最大詞元token的個數"emb_dim": 768,         # Embedding dimension 嵌入向量的緯度"n_heads": 12,          # Number of attention heads 多頭的頭數"n_layers": 12,         # Number of layers 神經網絡的層數"drop_rate": 0.1,       # Dropout rate 丟棄率，為了防止過擬合，會隨機丟棄10%的隱藏單元"qkv_bias": False       # Query-Key-Value bias qkv的偏置項開啟與否，默認是關閉
}

nn	用法
Embedding
Dropout
Sequential
Linear