算法基礎第3章數據結構

1.單調棧

1.什么是單調棧
單調棧，即具有單調性的棧。
實現

#include <iostream>
#include <stack>
using namespace std;
const int N = 3e6 + 10;
int a[N], n;
void test1()
{stack<int> st; // 維護?個單調遞增的棧for(int i = 1; i <= n; i++){// 棧???于等于 a[i] 的元素全部出棧while(st.size() && st.top() >= a[i]) st.pop();st.push(a[i]);}
}

2.單調棧解決的問題

尋找當前元素左側，離它最近，且比它大的元素在哪
尋找當前元素左側，離它最近，且比它小的元素在哪
尋找當前元素右側，離它最近，且比它大的元素在哪
尋找當前元素右側，離它最近，且比它小的元素在哪

雖然是四個問題，但是原理是?致的。因此，只要解決?個，舉?反三就可以解決剩下的幾個。

3.尋找當前元素左側，離它最近，并且比它大的元素在哪
從左往右遍歷元素，構造?個單調遞減的棧。插入當前位置的元素的時：
? 如果棧為空，則左側不存在比當前元素大的元素；
? 如果棧非空，若棧頂元素比當前位置大則棧頂元素為目標元素；若棧頂元素比當前元素小，出棧維護單調遞減棧。
注意，因為我們要找的是最終結果的位置。因此，棧里面存的是每個元素的下標。

1.1【模板】單調棧

P5788 【模板】單調棧

2.單調隊列

1.什么是單調隊列？
單調隊列，即存儲的元素要么單調遞增要么單調遞減的隊列，這里的隊列是個雙端隊列。
2.單調隊列解決的問題
一般用于解決滑動窗口內最大值最小值問題，以及優化動態規劃。

2.1 滑動窗口 /【模板】單調隊列

P1886 滑動窗口 /【模板】單調隊列

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<deque>
//https://www.luogu.com.cn/problem/P1886
using namespace std;
const int N = 1e6 + 10;
int n, k;
int a[N];
//單調隊列
int main()
{cin >> n >> k;for (int i = 1; i <= n; ++i)cin >> a[i];//存儲下標的雙端隊列deque<int> q;//找窗口內最小值for (int i = 1; i <= n; ++i){//單調遞增的隊列while (q.size() && a[i] <= a[q.back()])q.pop_back();q.push_back(i);//判斷是否在窗口內，并更新隊列if (q.size() && i - q.front() >= k)q.pop_front();//當窗口大小達到k時，取出窗口內的最值if (i >= k)cout << a[q.front()] << ' ';}cout << endl;q.clear();//找窗口內最大值for (int i = 1; i <= n; ++i){//單調遞減的隊列while (q.size() && a[i] >= a[q.back()])q.pop_back();q.push_back(i);//判斷是否在窗口內，并更新隊列if (q.size() && i - q.front() >= k)q.pop_front();//當窗口大小達到k時，取出窗口內的最值if (i >= k)cout << a[q.front()] << ' ';}cout << endl;return 0;
}

3.并查集

3.1并查集的概念及實現

3.1.2并查集的概念

并查集(Union Find）：是一種用于維護元素所屬集合的數據結構，實現為一個森林，其中每棵樹表示一個集合，樹中的節點表示對應集合中的元素，根節點來代表整個集合。

實現并查集的時，我們?般讓根節點自己指向自己。
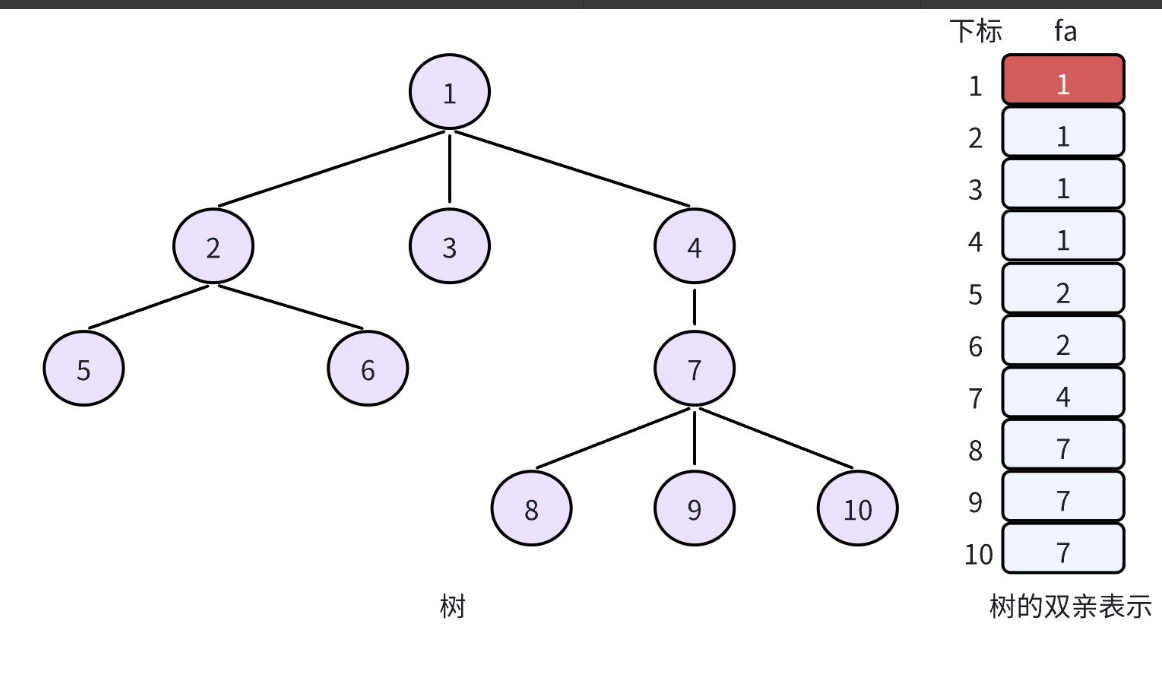
在這里插入圖片描述

我們需要維護若干個集合

查詢操作：查找x屬于哪一個集合
合并操作：將x所在集合和y所在集合合并成一個集合
判斷操作：判斷x和y是否在同一個集合

3.1.2并查集的實現

1.初始化：讓元素自己指向自己

for(int i=1;i<=n;i++)fa[i]=i;

2.查詢

// 返回父親節點
int find(int x)
{if(fa[x] == x) return x;//     路徑壓縮			把被查詢的節點到根節點的路徑上的所有節點的?節點設置為根節點return fa[x] = find(fa[x]);// ??實現return fa[x] == x ? x : fa[x] = find(fa[x]);
}

3.合并
將元素 x 所在的集合與元素 y 所在的集合合并成?個集合：

讓元素 x 所在樹的根節點指向元素 y 所在樹的根節點。

// 合并操作
void un(int x, int y) // 注意，函數名字不能? union，因為它是 C++ 的關鍵字
{int fx = find(x);int fy = find(y);// 讓元素 x 所在樹的根節點指向元素 y 所在樹的根節點。fa[fx] = fy;
}

4.判斷
判斷元素 x 和元素 y 是否在同?集合：

看看兩者所在樹的根節點是否相同。

// 合并操作
// 判斷是否在同?集合
bool issame(int x, int y)
{return find(x) == find(y);
}

3.2普通并查集

P3367 【模板】并查集

3.3拓展并查集

普通的并查集只能解決各元素之間僅存在?種相互關系，比如《親戚》題目中：
? a 和 b 是親戚關系， b 和 c 是親戚關系，這時就可以查找出 a 和 c 也存在親戚關系。

但如果存在各元素之間存在多種相互關系，普通并查集就無法解決。比如下面的案例：
? a和 b是敵?關系， b和 c是敵人關系，但是 a和 c其實不是敵人關系，而是另?種朋友關系。
此時，就不僅僅是簡單的敵?關系，還是出現?種朋友關系。
解決這類問題就需要對并查集進行擴展：將每個元素拆分成多個域，每個域代表?種狀態或者關系。
通過維護這些域之間的關系，來處理復雜的約束條件。

下例中，若1與2是敵人且2與3是敵人那么1和3就在同一個集合中，則1與3是朋友
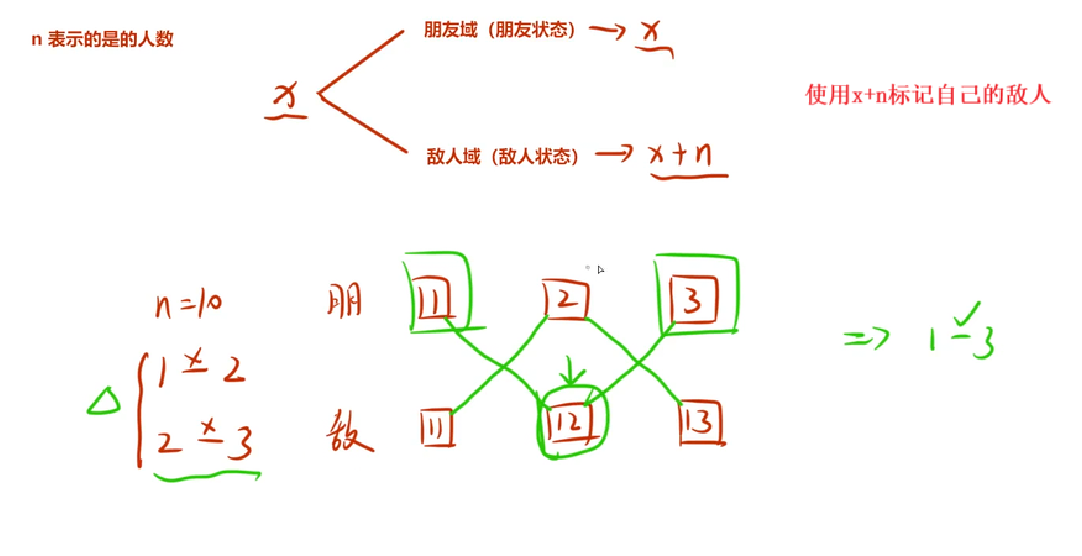
在這里插入圖片描述
以下題為例實現：關鍵在于將敵人的敵人合并
P1892 [BalticOI 2003] 團伙

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
//https://www.luogu.com.cn/problem/P1892
using namespace std;
const int N = 1e3 + 10;
// 拓展并查集int n, m, p, q;
char opt;
int fa[N*2];int find(int x)
{if (fa[x] == x)return x;return fa[x] = find(fa[x]);
}
// 使朋友域元素為父節點
void un(int x, int y)
{int fx = find(x), fy = find(y);fa[fy] = fx;
}
int main()
{cin >> n >> m;for (int i = 1; i <= 2 * n; ++i)fa[i] = i;while (m--){cin >> opt >> p >> q;if (opt == 'F'){un(p, q);}else{//敵人的敵人是朋友un(p, q + n);un(q, p + n);}}int res = 0;for (int i = 1; i <=  n; ++i){if (fa[i] == i)res++;}cout << res << endl;return 0;
}

3.4帶權并查集

1.帶權并查集的概念
帶權并查集在普通并查集的基礎上，為每個結點增加了?個權值。這個權值可以表示當前結點與父結點之間的關系、距離或其他信息（注意，由于我們有路徑壓縮操作，所以最終這個權值表示的是當前結點相對于根結點的信息）。有了這樣?個權值，就可以推斷出集合中各個元素之間的相互關系。
2.帶權并查集的實現
實現?個能夠查詢任意兩點之間距離的并查集。實現帶權并查集的核心是在進行 Find 和 Union 操作時，不僅要維護集合的結構，還要維護結點的權值。

基本操作：

const int N = 1e5 + 10, INF = 0x3f3f3f3f;
int n;
int fa[N], d[N];
// 初始化
void init()
{for(int i = 1; i <= n; i++){fa[i] = i;d[i] = 0; // 根據題?要求來初始化，這里表示到父節點距離}
}// 查詢操作
int find(int x)
{if(fa[x] == x) return x;int t = find(fa[x]); // 這句代碼?定要先執?，先縮短路徑// 更新到根節點的距離d[x] += d[fa[x]]; // 會根據權值的意義有所改變return fa[x] = t;
}// 合并操作
// x 所在集合與 y 所在集合合并，x 與 y 之間的權值是 w
void un(int x, int y, int w)
{int fx = find(x), fy = find(y);if(fx != fy) // 不在同?個集合中{fa[fx] = fy;// 更新到根節點的距離d[fx] = d[y] + w - d[x]; // 會根據權值的意義有所改變}
}

4.字符串哈希

什么是字符串哈希：
定義?個把字符串映射到整數的函數，這就是字符串哈希。即將?個字符串用一個整數表示。
字符串哈希中的哈希函數：
在字符串哈希中，有?種沖突概率較小的哈希函數，將字符串映射成 p 進制數字：
$\sum_{i=0}^{n-1} s[i] \times p^{n-i-1} \pmod{M}$
前綴哈希數組：
一般使用前綴和存儲每個前綴的哈希值，這樣的話每次就能快速求出子串的哈希了。

// 處理前綴哈希數組以及 p 的 i 次?數組
void init_hash()
{f[0] = 0; p[0] = 1;for(int i = 1; i <= len; i++){f[i] = f[i - 1] * P + s[i];p[i] = p[i - 1] * P;}
}// 快速求得任意區間的哈希值
ULL get_hash(int l, int r)
{return f[r] - f[l - 1] * p[r - l + 1];
}

將f[i]映射成p進制數，則f[i] = f[i - 1] * P + s[i];
若要求出中間某一段的哈希值，將目標字符串、f[r]、f[l-1]表示出來找出他們之間的關系，表示如下
在這里插入圖片描述

例子：
P3370 【模板】字符串哈希

5.Trie樹

Trie 樹又叫字典樹或前綴樹，是?種能夠快速插入和查詢字符串的數據結構。它利用字符串的公共前綴，將字符串組織成?棵樹形結構。
我們可以把字典樹想象成?棵多叉樹，每一條邊代表?個字符，從根節點到某個節點的路徑就代表了一個字符串。例如，要存儲 “abc” 、 “abd” 、 “acde” 以及 “cd” 時，構建的字典樹如下：
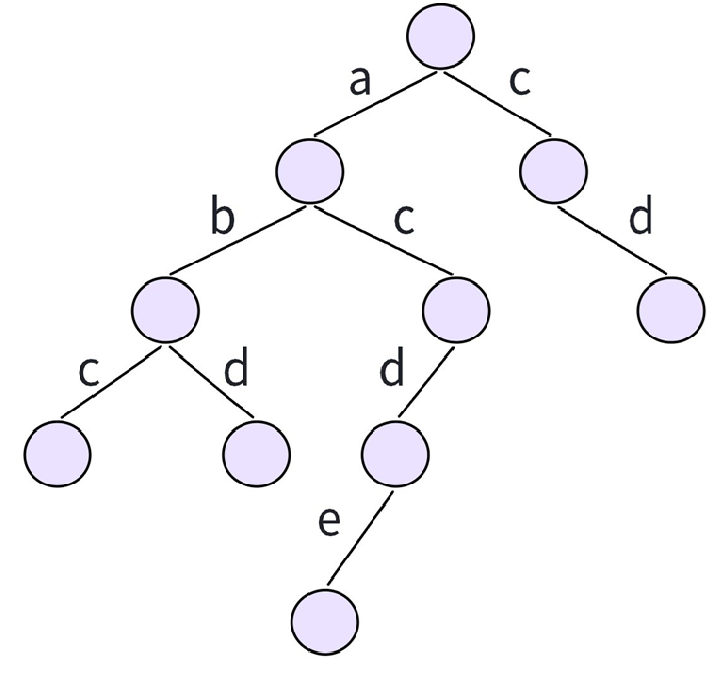
字典樹的作用
查詢某個單詞是否出現過，并且出現幾次；
查詢有多少個單詞是以某個字符串為前綴；
查詢所有以某個前綴開頭的單詞；（這個作用可以用到輸入法中，輸入拼音的時候，可以提示可能的單詞）
字典樹的實現
實現一個能夠查詢單詞出現次數以及查詢有多少個單詞是以某個字符串為前綴的字典樹，默認全是小寫字母。

// 字典樹        經過這個節點的字符串
int tr[N][62], p[N];
// 新插入節點的編號
int idx;
int t, n, q;
// 查詢是哪個字符
int get_num(char ch)
{if (ch >= 'a' && ch <= 'z')return ch - 'a';else if (ch >= 'A' && ch <= 'Z')return ch - 'A' + 26;else return ch - '0' + 52;
}// 插入字典樹
void insert(string& s)
{int cur = 0;// 從根結點開始p[cur]++;// 這個格?經過?次for (auto ch : s){int path = get_num(ch);if (tr[cur][path] == 0)tr[cur][path] = ++idx;// 迭代到下一個路徑cur = tr[cur][path];p[cur]++;}e[cur]++;
}
// 查詢特定前綴字符串個數
int find_pre(string& s)
{int cur = 0;for (auto ch : s){int path = get_num(ch);if (tr[cur][path] == 0)return 0;cur = tr[cur][path];}// 查詢從這個格子經過的所有字符串return p[cur];
}// 查詢字符串出現次數
int find(string& s)
{int cur = 0;for(auto ch : s){int path = ch - 'a';if(tree[cur][path] == 0) return 0;cur = tree[cur][path];}return e[cur];
}