離散化
講解
這里的離散化特指整數有序離散化。整個值域跨度很大,但是值非常稀疏的情況。
問題背景
我們有一個無限長的數軸,初始時每個位置上的值都是0。我們需要進行兩種操作:
- 修改操作:在某個位置?
x?上增加一個值?c。 - 查詢操作:詢問區間?
[l, r]?內所有位置的值之和。
數據范圍
- 操作次數?
n?和查詢次數?m?最多為?10^5。 - 坐標?
x?和區間端點?l,?r?的范圍是?-10^9?到?10^9。 - 修改值?
c?的范圍是?-10000?到?10000。
解題思路
由于坐標范圍非常大(-10^9 到 10^9),直接使用數組存儲每個位置的值會非常浪費空間。因此,我們需要使用離散化技術,將實際的坐標映射到一個小范圍內。
離散化步驟
- 收集所有需要離散化的值:包括所有的修改位置?
x?和查詢區間的端點?l?和?r。 - 排序并去重:對這些值進行排序,并去掉重復的值。
- 映射:將每個原始值映射到一個新的小范圍內的索引。
模板題
802. 區間和 - AcWing題庫
#include <bits/stdc++.h>
using namespace std;typedef pair<int, int> PII;
const int N = 300010;
int n, m;
int a[N], s[N]; // 存數數組與前綴和數組
vector<int> alls; // 存儲所有要離散化的值
vector<PII> add, query; // 添加與查詢// 二分查找找到 x 在 alls 中的位置
int find(int x) {int l = 0, r = alls.size() - 1;while (l < r) {int mid = l + r >> 1;if (alls[mid] >= x) r = mid;else l = mid + 1;}return r + 1; // 返回 x 映射后的位置
}int main() {cin >> n >> m;for (int i = 0; i < n; i++) {int x, c;cin >> x >> c;add.push_back({x, c});alls.push_back(x); // 收集需要離散化的值}for (int i = 0; i < m; i++) {int l, r;cin >> l >> r;query.push_back({l, r});alls.push_back(l);alls.push_back(r); // 收集需要離散化的值}// 對 alls 排序并去重sort(alls.begin(), alls.end());alls.erase(unique(alls.begin(), alls.end()), alls.end());// 處理插入操作for (auto item : add) {int x = find(item.first); // 找到 x 映射后的位置a[x] += item.second; // 在該位置增加 c}// 預處理前綴和for (int i = 1; i <= alls.size(); i++) s[i] = s[i - 1] + a[i];// 處理查詢操作for (auto item : query) {int l = find(item.first), r = find(item.second); // 找到 l 和 r 映射后的位置cout << s[r] - s[l - 1] << endl; // 輸出區間 [l, r] 的和}return 0;
}模板題講解
pair 是為了 把“有關系的兩個數據”綁在一起,方便一起存儲和使用。
在本題中:
add?操作需要兩個數:位置?x?和?要加的值?cquery?查詢也需要兩個數:左端點?l?和?右端點?r
我們用 pair<int, int> 把它們“配對”起來,這樣就不會搞混。
想象你在記賬:
| 時間 | 事件 |
|---|---|
| 3點 | 在超市花 50 元 |
| 5點 | 在餐廳花 100 元 |
你想記錄這些操作,你會怎么存?錯誤方式:
vector<int> times = {3, 5};
vector<int> money = {50, 100};問題:如果排序或刪除,很容易“時間”和“金額”對不上!
vector<pair<int, int>> records = {{3, 50}, {5, 100}};這樣,3點 和 50元 永遠是一對,不會錯亂。
再回到題目:vector<PII> add;?—— 存修改操作
for (int i = 0; i < n; i++) {int x, c;cin >> x >> c;add.push_back({x, c}); // 把“位置x”和“加的值c”綁在一起
}比如輸入:
1 2
3 6
7 5add 變成:
add = { {1,2}, {3,6}, {7,5} }{1,2}?表示:在位置 1 加 2{3,6}?表示:在位置 3 加 6
好處:后面遍歷的時候,item.first 就是 x,item.second 就是 c。
find函數的作用是什么?
int find(int x) {int l = 0, r = alls.size() - 1; // l=左邊界,r=右邊界while (l < r) { // 二分查找開始int mid = l + r >> 1; // 相當于 (l + r) / 2,找中間位置if (alls[mid] >= x) // 如果中間的數 >= xr = mid; // 說明 x 在左邊,把右邊界縮小到 midelse // 如果中間的數 < xl = mid + 1; // 說明 x 在右邊,把左邊界移到 mid+1}return r + 1; // 返回位置(+1 是因為窗口號從 1 開始,且r是下標,從0開始)
}這個 find 函數,就是在一個排好序的列表里,快速找到某個數 x 的“排名”(位置),然后返回它的“新編號”。find(x) 就像查字典:給你一個詞(x),快速找到它在詞典(alls)里的頁碼(新編號),方便后面查數據。
舉個生活例子:排隊領號
想象你去銀行辦事:
- 銀行有 10 個窗口,但今天只有 3 個人來辦業務,他們的號碼是:
1, 3, 7 - 銀行不想浪費窗口資源,于是說:“我們重新分配窗口號!”
- 把這三個號碼?從小到大排序,然后按順序分配新窗口號:
1?→ 窗口 13?→ 窗口 27?→ 窗口 3
這個過程就叫 離散化:把很大的原始號碼(比如 1億),映射到很小的窗口號(1,2,3)。
在你的代碼里,alls 就是那個“排好序的號碼列表”。比如:
alls = {1, 3, 7} // 原始坐標,已經排序去重我們想問:
“原始坐標
3對應哪個窗口號?”
答案是:第 2 個位置 → 所以返回 2
| 原始坐標 x | 在 alls 中的下標 | 返回值(r+1) | 新編號 |
|---|---|---|---|
| 1 | 0 | 0+1 = 1 | 1 |
| 3 | 1 | 1+1 = 2 | 2 |
| 7 | 2 | 2+1 = 3 | 3 |
為什么用二分?不用直接找?
因為 alls 可能有 30 萬個數,如果一個一個找(線性查找),太慢了!
- 線性查找:最多要查 30 萬次
- 二分查找:最多查?
log?(30萬) ≈ 19?次
?快了上萬倍!
處理修改與查詢操作
第一部分:處理修改操作
for (int i = 0; i < n; i++) {int x, c;cin >> x >> c; // 讀入位置 x 和要加的值 cadd.push_back({x, c}); // 把 (x, c) 存起來,后面要用alls.push_back(x); // 把 x 記錄下來,準備離散化!
}| i | x | c | add?變成 | alls?變成 |
|---|---|---|---|---|
| 0 | 1 | 2 | {1,2} | {1} |
| 1 | 3 | 6 | {1,2},{3,6} | {1,3} |
| 2 | 7 | 5 | {1,2},{3,6},{7,5} | {1,3,7} |
所以現在:
add?存了所有“在哪加、加多少”alls?存了所有被修改過的位置:1, 3, 7
第二部分:處理查詢操作
for (int i = 0; i < m; i++) {int l, r;cin >> l >> r; // 讀入查詢區間 [l, r]query.push_back({l, r}); // 把 (l, r) 存起來,后面要用alls.push_back(l); // 把 l 記下來,也要離散化!alls.push_back(r); // 把 r 記下來,也要離散化!
}| i | l | r | query?變成 | alls?新增 |
|---|---|---|---|---|
| 0 | 1 | 3 | {1,3} | 1, 3?→?alls = {1,3,7,1,3} |
| 1 | 4 | 6 | {1,3},{4,6} | 4,6?→?alls = {1,3,7,1,3,4,6} |
| 2 | 7 | 8 | {1,3},{4,6},{7,8} | 7,8?→?alls = {1,3,7,1,3,4,6,7,8} |
為什么查詢的?l?和?r?也要放進?alls?
因為我們要對所有出現過的坐標進行離散化!
你想啊,后面要查 [4,6] 的和,但 4 和 6 這兩個位置根本沒人改過,它們不在 add 里。
但我們必須知道:
4?在離散化后對應哪個編號?6?在離散化后對應哪個編號?
否則沒法查區間!
所以:只要是出現過的坐標(無論是修改還是查詢),都要放進 alls!
后面代碼會做兩件事:
sort(alls.begin(), alls.end());
alls.erase(unique(alls.begin(), alls.end()), alls.end());排序 + 去重后變成:
{1, 3, 4, 6, 7, 8}然后我們就可以離散化了:
| 原始坐標 | 新編號(find 返回) |
|---|---|
| 1 | 1 |
| 3 | 2 |
| 4 | 3 |
| 6 | 4 |
| 7 | 5 |
| 8 | 6 |
處理插入,預處理前綴和,處理詢問(輸出每個區間的和)
第一段:處理插入(把值加到離散化后的位置)
for (auto item : add) {int x = find(item.first); // 找到原始位置對應的新編號a[x] += item.second; // 把值加到新位置上
}第一次:item = {1,2}
item.first = 1?→?find(1) = 1?→?x = 1a[1] += 2?→?a[1] = 2
第二次:item = {3,6}
find(3) = 2?→?x = 2a[2] += 6?→?a[2] = 6
第三次:item = {7,5}
find(7) = 5?→?x = 5a[5] += 5?→?a[5] = 5
現在 a 數組長這樣(只看 1~6):
| 新編號 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 值 a[i] | 2 | 6 | 0 | 0 | 5 | 0 |
注意:a[i] 存的是離散化后編號為 i 的位置上的值
第二段:預處理前綴和
for (int i = 1; i <= alls.size(); i++)s[i] = s[i - 1] + a[i];alls.size() = 6,所以 i 從 1 到 6
我們來算 s[i],它表示:前 i 個離散化位置的值的總和
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| s[i] | 0 | 2 | 8 | 8 | 8 | 13 | 13 |
第三段:處理詢問(輸出每個區間的和)
for (auto item : query) {int l = find(item.first), r = find(item.second);cout << s[r] - s[l - 1] << endl;
}舉個例子
查詢 1:item = {1,3}?→ 查?[1,3]?的和
l = find(1) = 1r = find(3) = 2- 輸出:
s[2] - s[1 - 1] = s[2] - s[0] = 8 - 0 = 8
區間合并
講解
區間合并就是對區間求并集。
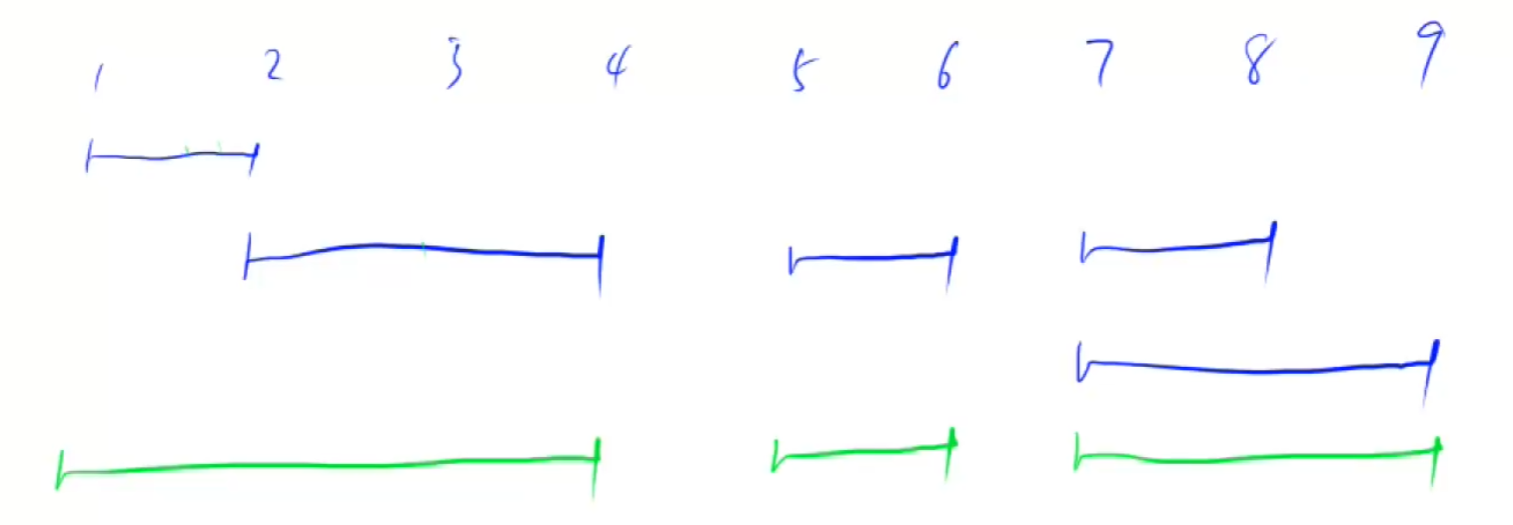
給定一些區間,比如 [1,3] 和 [2,6],如果這些區間有交集(包括端點相交),我們就需要把它們合并成一個更大的區間。最終我們要計算合并后剩下多少個不重疊的區間。
我們可以看到:
[1, 2]?和?[2, 4]?有交集,可以合并成?[1, 4][7, 8]?和?[7, 9]?有交集,可以合并成?[7, 9][5, 6]?沒有和其他區間交集,保持不變
所以最終合并后的區間是:
[1, 4][5, 6][7, 9]
因此,合并后的區間個數是 3。
模板題
AcWing 803. 區間合并 - AcWing
#include <bits/stdc++.h>
using namespace std;typedef pair<int, int> PII;// 合并區間的函數
void merge(vector<PII> &segs) {// 結果數組,存儲合并后的區間vector<PII> res;// 對輸入的區間按照起始位置進行排序sort(segs.begin(), segs.end());// 初始化當前區間的起始和結束位置int st = -2e9, ed = -2e9;// 遍歷所有區間for (auto seg : segs) {// 如果當前區間的起始位置大于上一個區間的結束位置if (ed < seg.first) {// 如果st不是初始值,說明之前已經有一個區間了,將其加入結果數組if (st != -2e9) {res.push_back({st, ed});}// 更新當前區間的起始和結束位置st = seg.first, ed = seg.second;} else {// 如果當前區間的起始位置小于等于上一個區間的結束位置,說明有交集// 更新當前區間的結束位置為兩者中的較大值ed = max(ed, seg.second);}}// 最后檢查是否有剩余的區間未加入結果數組if (st != -2e9) {res.push_back({st, ed});}// 將結果數組賦值給原數組,完成合并操作segs = res;
}int main() {// 區間數量int n;cin >> n;// 創建一個vector來存儲所有的區間vector<PII> segs;// 讀取每個區間并存入vector中for (int i = 0; i < n; i++) {int l, r;cin >> l >> r;segs.push_back({l, r});}// 調用merge函數進行區間合并merge(segs);// 輸出合并后的區間個數cout << segs.size() << endl;return 0;
}模板題講解
int st = -2e9, ed = -2e9; 這一步是怎么來的?
目的是初始化一個“虛擬”的起始區間,用來方便地處理第一個真實區間的合并邏輯。
注意:-2e9 就是 -2 * 10^9,題目說區間范圍是 -10^9 ≤ li ≤ ri ≤ 10^9,所以 -2e9 比所有可能的左端點都小,可以當作“負無窮”。
int st = -2e9, ed = -2e9; // 初始狀態:沒有正在合并的區間
for (auto seg : segs) {if (ed < seg.first) { // 當前區間無法和 seg 合并(斷開了)if (st != -2e9) { // 如果 st 不是初始值,說明我們之前已經在合并某個真實區間res.push_back({st, ed}); // 把之前合并好的區間存進去}// 開啟一個新的合并區間:就是當前這個 segst = seg.first;ed = seg.second;} else {// 能合并!更新當前合并區間的右邊界ed = max(ed, seg.second);}
}
// 循環結束后,最后一個正在合并的區間還沒加入結果
if (st != -2e9) {res.push_back({st, ed});
}為什么需要這個“虛擬起點”?
是為了統一處理邏輯,避免寫一堆 if (第一個區間) 的判斷。
比如如果沒有這個技巧,你可能會寫:
if (res.empty()) {st = seg.first;ed = seg.second;
} else if (ed < seg.first) {res.push_back({st, ed});st = seg.first;ed = seg.second;
} else {ed = max(ed, seg.second);
}int st = -2e9, ed = -2e9; 是一種編程技巧,叫做“哨兵”或“虛擬初始值”,作用是:
- 讓你在處理第一個真實區間時,也能套用統一的邏輯;
- 用?
st != -2e9?來判斷“是否已經開始合并一個真實區間”; - 避免特判第一個元素,讓代碼更簡潔、不易出錯。








)
)




)


》學習筆記ch4)

