題目描述
請設計一個文件緩存系統,該文件緩存系統可以指定緩存的最大值(單位為字節)。
文件緩存系統有兩種操作:
- 存儲文件(put)
- 讀取文件(get)
操作命令為:
- put fileName fileSize
- get fileName
存儲文件是把文件放入文件緩存系統中;
讀取文件是從文件緩存系統中訪問已存在,如果文件不存在,則不作任何操作。
當緩存空間不足以存放新的文件時,根據規則刪除文件,直到剩余空間滿足新的文件大小位置,再存放新文件。
具體的刪除規則為:文件訪問過后,會更新文件的最近訪問時間和總的訪問次數,當緩存不夠時,按照第一優先順序為訪問次數從少到多,第二順序為時間從老到新的方式來刪除文件。
輸入描述
第一行為緩存最大值 m(整數,取值范圍為 0 < m ≤ 52428800)
第二行為文件操作序列個數 n(0 ≤ n ≤ 300000)
從第三行起為文件操作序列,每個序列單獨一行,文件操作定義為:
op file_name file_size
file_name 是文件名,file_size 是文件大小
輸出描述
輸出當前文件緩存中的文件名列表,文件名用英文逗號分隔,按字典順序排序,如:
a,c
如果文件緩存中沒有文件,則輸出NONE
備注
- 如果新文件的文件名和文件緩存中已有的文件名相同,則不會放在緩存中
- 新的文件第一次存入到文件緩存中時,文件的總訪問次數不會變化,文件的最近訪問時間會更新到最新時間
- 每次文件訪問后,總訪問次數加1,最近訪問時間更新到最新時間
- 任何兩個文件的最近訪問時間不會重復
- 文件名不會為空,均為小寫字母,最大長度為10
- 緩存空間不足時,不能存放新文件
- 每個文件大小都是大于 0 的整數
用例1
輸入:
50
6
put a 10
put b 20
get a
get a
get b
put c 30
輸出:
a,c
用例2
輸入:
50
1
get file
輸出:
NONE
思考
輸入有讀取和存儲兩個操作。定義集合 fileSet 存儲文件名稱,哈希表 fileSizeMap 存儲映射每個文件的大小,key 是文件名,value 是文件大小,readFreqMap 存儲映射每個文件的讀取頻次,priorityQueue 維護一個文件名隊列,每次出隊的都是最久未被讀取的文件名。 讀取操作:如果讀取的文件不存在,就不執行任何操作;如果文件存在就給該文件的訪問頻次+1,同時調整優先隊列,把讀取的文件名移到隊尾,每次這樣操作,隊首的文件一定的最久未被訪問的文件。存儲操作:每次存儲文件判斷文件名是否存在,存在就不執行操作;如果不存在,判斷剩余存儲空間 leftSize 是否大于等于當前文件大小,如果不滿足就要刪除讀取頻次最少且最久未被訪問的文件,更新 leftSize += deleteFileSize,循環執行此操作直到滿足存儲需求,如果文件都刪完了還是不滿足就不執行任何操作。存儲文件到 fileSet 中,更新 leftSize -= newFileSize,題目要求存儲新文件也要更新最新訪問時間,那么我們就把新文件名加到優先隊列的隊尾,優先隊列隊尾文件名始終表示最新訪問的文件。刪除操作:首先查找訪問頻次最少的文件名,如果只有一個最少的訪問頻次,直接刪這個文件就對了。如果有多個相同的最少訪問頻次文件名,需要進一步在其中找到最久未被訪問的文件,顯然由于每次優先隊列的隊尾都是更新最新訪問時間的文件名,隊首的文件就是最久未被訪問的,遍歷優先隊列找到最少訪問頻次文件集合中包含當前文件名的文件中止循環,刪除該文件。為什么還遍歷隊列匹配最少訪問頻次集合中的文件?難道隊列隊首文件名可能不在最少訪問頻次文件集合中?有可能的,雖然隊首文件名是最久未被訪問的,但是未必就是訪問頻次最少的文件,假如有個文件 a 在歷史訪問記錄中達到了100次,接著存儲了一個新文件 b,這時候文件 b 是最新訪問的文件,存在隊尾,那么 顯然 a 是存在隊首的最久未被訪問的文件,但它的訪問頻率達到100次,b 只有一次,顯然不能直接刪除隊首元素 a 。由于 JavaScript 沒有優先隊列 API,如果不熟悉,做題的時候寫個正確的優先隊列數據結構也不容易,因此我先用 JS 數組模擬優先隊列的特性實現這個算法,實際能在有效時間內通過所有測試用例才是最重要的。然后提供一個 JS 版二叉堆實現的優先隊列版本代碼。
算法過程(哈希表+數組模擬優先隊列)
-
數據結構:
- 用
fileSet記錄緩存中的文件;fileSizesMap存儲文件大小;readFreqMap記錄訪問次數;priorityQueue(數組)按訪問時間排序(最新訪問在末尾)。 leftSize追蹤剩余緩存空間。
- 用
-
核心操作:
put操作:- 若文件已存在,直接跳過。
- 若緩存空間不足,按規則淘汰文件:先篩選訪問次數最少的文件列表,再從列表中刪除
priorityQueue中最早出現(最久未訪問)的文件,直到空間足夠。 - 空間足夠時,新增文件至緩存,初始化訪問次數為0,加入
priorityQueue末尾。
get操作:- 若文件存在,訪問次數+1,從
priorityQueue中移除后重新加入末尾(更新為最新訪問)。
- 若文件存在,訪問次數+1,從
-
結果輸出:
緩存中的文件按字典排序,空則輸出NONE。
時間復雜度
- 單次
put操作:- 淘汰文件時,遍歷查找最少訪問次數文件的時間為
O(k)(k為當前緩存文件數),最壞情況下需淘汰k次,總復雜度為O(k2)。 - 新增文件為
O(1)。
- 淘汰文件時,遍歷查找最少訪問次數文件的時間為
- 單次
get操作:- 查找并移動文件在
priorityQueue中的位置為O(k)。
- 查找并移動文件在
- 整體復雜度:
設操作總數為n,單個操作涉及的最大文件數為k(≤緩存可容納的最大文件數),總時間復雜度為O(n·k2)。
(注:因k通常遠小于n,實際性能可接受,尤其適合中小規模操作場景。)
參考代碼(Least Frequence Used + JS 數組模擬優先隊列)
function solution(totalSize, operations) {const fileSet = new Set();const fileSizesMap = new Map();const readFreqMap = new Map();const priorityQueue = [];let leftSize = totalSize;for (const operation of operations) {const [op, fileName, fileSize] = operation;if (op === 'put') {if (fileSet.has(fileName)) {continue;}// 緩存不夠,要刪文件while (leftSize - fileSize < 0 && priorityQueue.length) {let count = Infinity;let toDeleteList = [];for (let [k, v] of readFreqMap) { // 查找訪問頻率最少的文件if (v < count) {toDeleteList = [k];count = v;} else if (v === count) {toDeleteList.push(k);}}if (toDeleteList.length === 1) { // 如果找到一個訪問頻率最少的文件直接刪除fileSet.delete(toDeleteList[0]);const delSize = fileSizesMap.get(toDeleteList[0]);leftSize += delSize;readFreqMap.delete(toDeleteList[0]);let index = priorityQueue.indexOf(toDeleteList[0]);priorityQueue.splice(index, 1);} else { // 多個訪問頻率最少的文件需要篩選最久未被訪問的文件,然后刪除for (let i = 0; i < priorityQueue.length; i++) {if (toDeleteList.includes(priorityQueue[i])) {let deleteFileName = priorityQueue[i];fileSet.delete(deleteFileName);const delSize = fileSizesMap.get(deleteFileName);leftSize += delSize;priorityQueue.splice(i, 1);readFreqMap.delete(deleteFileName);break;}}} }if (leftSize - fileSize >= 0) {fileSet.add(fileName);fileSizesMap.set(fileName, fileSize);readFreqMap.set(fileName, 0);priorityQueue.push(fileName);leftSize -= fileSize;console.log('leftSize: ', leftSize, ' fileSize: ', fileSize);}} else { // getif (fileSet.has(fileName)) {readFreqMap.set(fileName, readFreqMap.get(fileName) + 1); // 更新訪問頻率let index = priorityQueue.indexOf(fileName);if (index !== -1) {priorityQueue.splice(index, 1);}priorityQueue.push(fileName); // 移到訪問隊列隊首,表示最新訪問的文件 }}}const fileList = Array.from(fileSet);fileList.sort();let result = "NONE";if (!fileList.length) {console.log("NONE");return "NONE";}result = fileList.join(',');console.log(result);return result;
}const cases = [`50
6
put a 10
put b 20
get a
get a
get b
put c 30`, `50
1
get file`
];let caseIndex = 0;
let lineIndex = 0;const readline = (function () {let lines = [];return function () {if (lineIndex === 0) {lines = cases[caseIndex].trim().split("\n").map((line) => line.trim());}return lines[lineIndex++];};
})();cases.forEach((_, i) => {caseIndex = i;lineIndex = 0;// console.time(`${i} cost time`);solution();// console.timeEnd(`${i} cost time`); console.log('-------');
});算法過程(優先隊列)
-
數據結構:
- 核心使用
MinPriorityQueue(最小優先隊列,基于堆實現)存儲文件信息,堆的比較規則為“訪問次數少優先,次數相同則時間早優先”。 _cache(Map)快速映射文件名到文件詳情(大小、訪問次數、時間戳);_usedSize記錄已用緩存空間;_timeCount生成唯一時間戳。
- 核心使用
-
核心操作:
put操作:- 若文件已存在或大小超緩存上限,直接跳過。
- 若緩存空間不足,循環刪除堆頂元素(優先級最高的待淘汰文件),直到空間足夠。
- 新增文件至
_cache和堆,初始化訪問次數為0,更新時間戳和已用空間。
get操作:- 若文件存在,先從堆中刪除該文件(通過替換+堆調整實現),再更新其訪問次數和時間戳,重新加入堆。
-
堆調整細節:
- 中間刪除元素時,用堆尾元素替換目標位置,再通過
swim(上浮)和sink(下沉)確保堆結構正確。 - 堆頂始終是“訪問次數最少且最久未訪問”的文件,淘汰時直接刪除堆頂。
- 中間刪除元素時,用堆尾元素替換目標位置,再通過
-
結果輸出:
緩存中的文件按字典排序,空則輸出NONE。
時間復雜度
- 單次
put操作:- 入隊(
enqueue)和出隊(dequeue)均為堆操作,時間復雜度O(log k)(k為當前緩存文件數)。 - 最壞情況下需淘汰
k個文件,總復雜度O(k·log k)。
- 入隊(
- 單次
get操作:- 查找文件在堆中的位置為
O(k),刪除并重新入隊為O(log k),總復雜度O(k + log k)。
- 查找文件在堆中的位置為
- 整體復雜度:
設操作總數為n,總時間復雜度為O(n·k·log k)(k為緩存中最大文件數)。
(注:堆優化了淘汰階段的查找效率,相比數組模擬的O(k2),在大k場景下性能更優。)
參考代碼(Least Frequence Used + 最小優先隊列)
class MinPriorityQueue {constructor(compare) {this._data = [];this._compare = compare || ((a, b) => a - b);}enqueue(e) {this._data.push(e);this.swim(this._data.length-1);}dequeue() {if (this.isEmpty()) return null;const last = this._data.pop();if (this._data.length > 0) {this._data[0] = last;this.sink(0);}}swim(index) {while (index > 0) {let parentIndex = Math.floor((index - 1) / 2);if (this._compare(this._data[index], this._data[parentIndex]) < 0) {[this._data[parentIndex], this._data[index]] = [this._data[index],this._data[parentIndex],];index = parentIndex;continue;}break;}}// 從指定索引開始下沉sink(index) {const n = this._data.length;while (true) {let left = 2 * index + 1;let right = left + 1;let smallest = index;if (left < n && this._compare(this._data[left], this._data[index]) < 0) {smallest = left;}if (right < n && this._compare(this._data[right], this._data[smallest]) < 0) {smallest = right;}if (smallest !== index) {[this._data[smallest], this._data[index]] = [this._data[index],this._data[smallest],];index = smallest;continue;}break;}}front() {return this._data[0];}isEmpty() {return this._data.length === 0;}size() {return this._data.length;}
}class LFUCacheSystem {constructor(capibility) {this._capibility = capibility; // 最大緩存大小this._usedSize = 0; // 當前使用的緩存大小this._cache = new Map();this._minHeap = new MinPriorityQueue((a, b) => { // 傳入自定義比較函數if (a.accessCount === b.accessCount) {return a.lastAccessTime - b.lastAccessTime; // 訪問頻次相同再比較訪問時間}return a.accessCount - b.accessCount;});this._timeCount = 0;}put(fileName, fileSize) {if (fileSize > this._capibility) return;if (this._cache.has(fileName)) { // 如果文件已存在,更新文件的訪問時間return;}// 緩存不夠用了,從最小優先隊列中刪除優先級最高的文件(訪問頻次最少且最久未被訪問的文件)while (fileSize + this._usedSize > this._capibility) {const toDelete = this._minHeap.front();if (toDelete) {this._minHeap.dequeue(); // 刪除文件this._cache.delete(toDelete.fileName);this._usedSize -= toDelete.size; // 更新可用緩存大小}}const currentTime = this._timeCount++;const file = { fileName, size: fileSize, accessCount: 0, lastAccessTime: currentTime };this._minHeap.enqueue(file);this._cache.set(fileName, file);this._usedSize += file.size;}get(fileName) {if (!this._cache.has(fileName)) return;const file = this._cache.get(fileName);this._removeFileFromHeap(fileName);file.accessCount++;file.lastAccessTime = this._timeCount++;this._minHeap.enqueue(file);}_removeFileFromHeap(fileName) {const index = this._minHeap._data.findIndex(item => item.fileName === fileName);if (index === -1) return;// 用最后一個元素替換目標元素const last = this._minHeap._data[this._minHeap._data.length-1];this._minHeap._data[index] = last;this._minHeap._data.pop();if (index < this._minHeap._data.length) {this._minHeap.swim(index);this._minHeap.sink(index);}}getFileList() {const fileList = Array.from(this._cache.keys());fileList.sort();return fileList;}
};function solution2(totalSize, ops) {const cacheSys = new LFUCacheSystem(totalSize);for (const op of ops) {const [operation, fileName, fileSize] = op;if (operation === 'put') {cacheSys.put(fileName, parseInt(fileSize));} else { // getcacheSys.get(fileName);}}const fileList = cacheSys.getFileList();let result = "NONE";if (!fileList.length) {console.log("NONE");return "NONE";}result = fileList.join(',');console.log(result);return result;
}function entry() {const totalSize = parseInt(readline());const n = parseInt(readline());const ops = [];for (let i = 0; i < n; i++) {const [op, fileName, fileSize] = readline().split(' ');ops.push([op, fileName, parseInt(fileSize)]);}// console.log('case: totalSize n ops ', totalSize, n, ops);// solution1 // const result = solution(totalSize, ops);// solution2const result2 = solution2(totalSize, ops);// console.log(result === result2);}const cases = [`50
6
put a 10
put b 20
get a
get a
get b
put c 30`, `50
1
get file`
];// 生成隨機 300000 個 put/get 操作用例,文件名最多100個不重復,超過26個字母范圍用數字后綴
(function(){const ops = [];const fileNames = [];let totalFiles = 0;const maxFiles = 100;const maxFileSize = 100;const totalOps = 300000;const cacheSize = 1000;function getFileName(idx) {if (idx < 26) {return String.fromCharCode(97 + idx); // 'a' ~ 'z'} else {return String.fromCharCode(97 + (idx % 26)) + (Math.floor(idx / 26));}}for (let i = 0; i < totalOps; i++) {if (Math.random() < 0.5 || totalFiles === 0) {// put 操作let idx = Math.floor(Math.random() * maxFiles);let fileName = getFileName(idx);let fileSize = Math.floor(Math.random() * maxFileSize) + 1;ops.push(`put ${fileName} ${fileSize}`);if (!fileNames.includes(fileName)) {fileNames.push(fileName);totalFiles++;}} else {// get 操作let fileName = fileNames[Math.floor(Math.random() * fileNames.length)];ops.push(`get ${fileName}`);}}const input = `${cacheSize}\n${totalOps}\n${ops.join('\n')}`;cases.push(input);
})();let caseIndex = 0;
let lineIndex = 0;const readline = (function () {let lines = [];return function () {if (lineIndex === 0) {lines = cases[caseIndex].trim().split("\n").map((line) => line.trim());}return lines[lineIndex++];};
})();caseIndex = 0;
lineIndex = 0;
cases.forEach((_, i) => {caseIndex = i;lineIndex = 0;entry();console.log('-------');
});驗證
兩種方法測試結果相同:
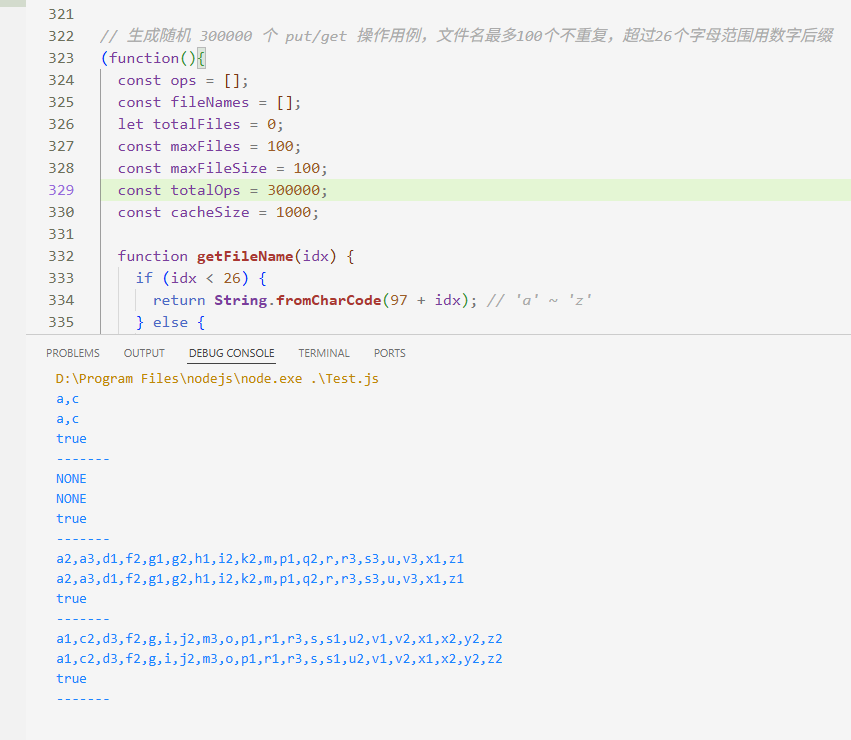


)

解鎖)




)


貪吃蛇項目2.貪吃蛇項目實現)


)
)

如何寫一個好的 Prompt)
