L2正則化:

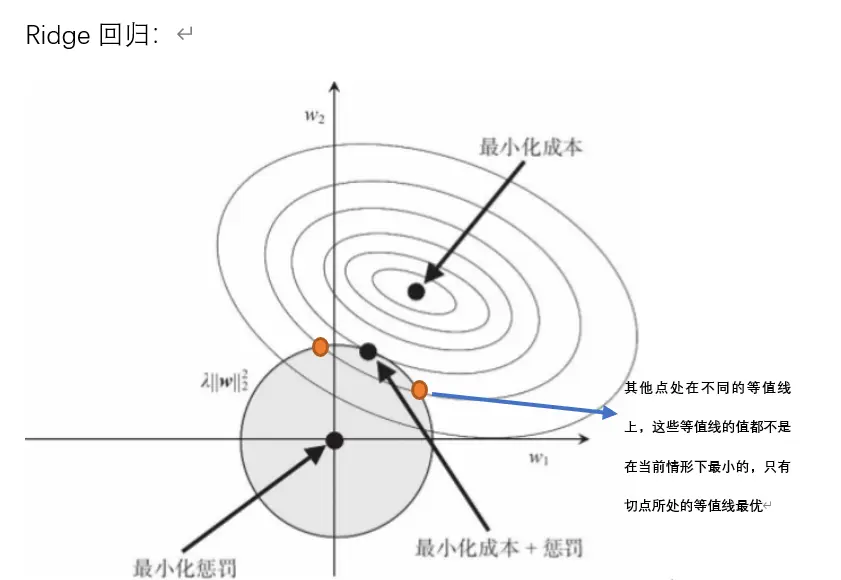
圖中用幾何方式形象地解釋了 Ridge 回歸（L2正則化）的原理。

① 陰影圓：可以理解為（w1^2 + w2^2）?≤R^2，圓周表示目標函數的約束線，這個圓表示了我們的參數?(w1,w2)可以活動的范圍。

• 為什么要約束？?因為如果權重太大，模型在訓練集上可能表現極好（擬合很好），但在新數據上的表現會大幅下降（過擬合）。
• R 越小意味著什么？圓變小，給權重的空間就越小，懲罰越強，模型更簡單，更不容易過擬合。R 越大，模型約等于普通線性回歸（無正則化）。

② 最小化成本點（最小二乘估計點）：在圖中心的黑點，就是普通線性回歸的最小二乘解，也就是“擬合訓練數據最好的點”

• 用等高線（橢圓）表現：圖里一圈一圈的橢圓，代表對于不同?(w1,w2)參數組合的損失（成本）大小。
  • 離中心越近，損失越小（擬合訓練集效果越好）。
  • 離中心越遠，損失越大（擬合效果變差）。
• 過擬合的風險：最小化成本點其實對訓練集來說是最優解，但往往會過擬合，也就是在新數據上表現很差。所以我們不總是選這個點作為模型的最終解。

我們的目標：不是單純讓損失最小，而是讓損失和權重大小都要“

約束下的最優解是什么？

• 如果沒有約束，解就在最小化成本點（中心）。
• 有了約束之后，我們只能在圓內找解：我們希望找一個既讓損失足夠小，又不會讓參數過大（也就是不過擬合）。

最終解的位置：

• 這就是圖里圓和某個等高線“剛好相切”的那個點，既滿足了“損失盡量小”，又不超出圓圈（不讓參數過大）。這個點就是 帶有L2懲罰的解。

L1正則化:

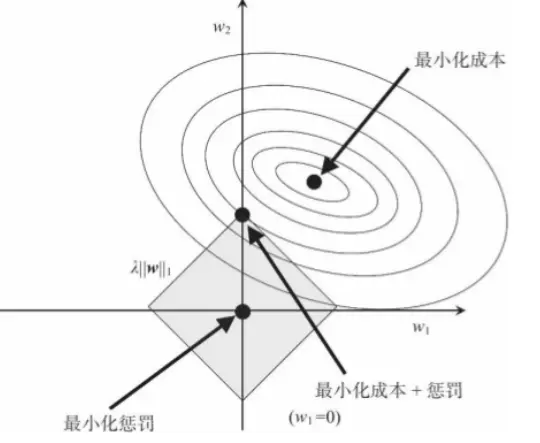
L1, L2 的區別

對于 L2 來說，限定區域是圓，這樣，得到的解 w1 或 w2 為 0 的概率很小，很大概率是非零的。

對于 L1 來說，限定區域是正方形，方形的最優解位置通常是在是尖銳點，這從視覺和常識上來看是很容易理解的。也就是說，方形的凸點會更接近最優解對應的 w 位置，而從圖中我們可以知道凸點處必有 w1 或 w2 為 0。這樣，得到的解 w1 或 w2 為零的概率就很大了。

reference:

以幾何思維理解L1&L2正則化 - 簡書

(5 封私信) 【通俗易懂】機器學習中 L1 和 L2 正則化的直觀解釋 - 知乎