論文閱讀|ArxiV 2024|Mamba進一步研究|VSSD

論文地址：pdf
代碼地址：code

文章目錄

1.研究背景與動機
2. 核心方法
- 2.1 預備知識:mamba-ssm
- 2.2 非因果狀態空間對偶性
- 2.3 視覺狀態空間對偶性模型
3. 實驗結果
- 3.1 圖像分類任務
- 3.2 目標檢測任務
- 3.3 語義分割任務
- 3.4 消融實驗
4.局限性與結論
- 4.1 局限性
- 4.2 結論

1.研究背景與動機

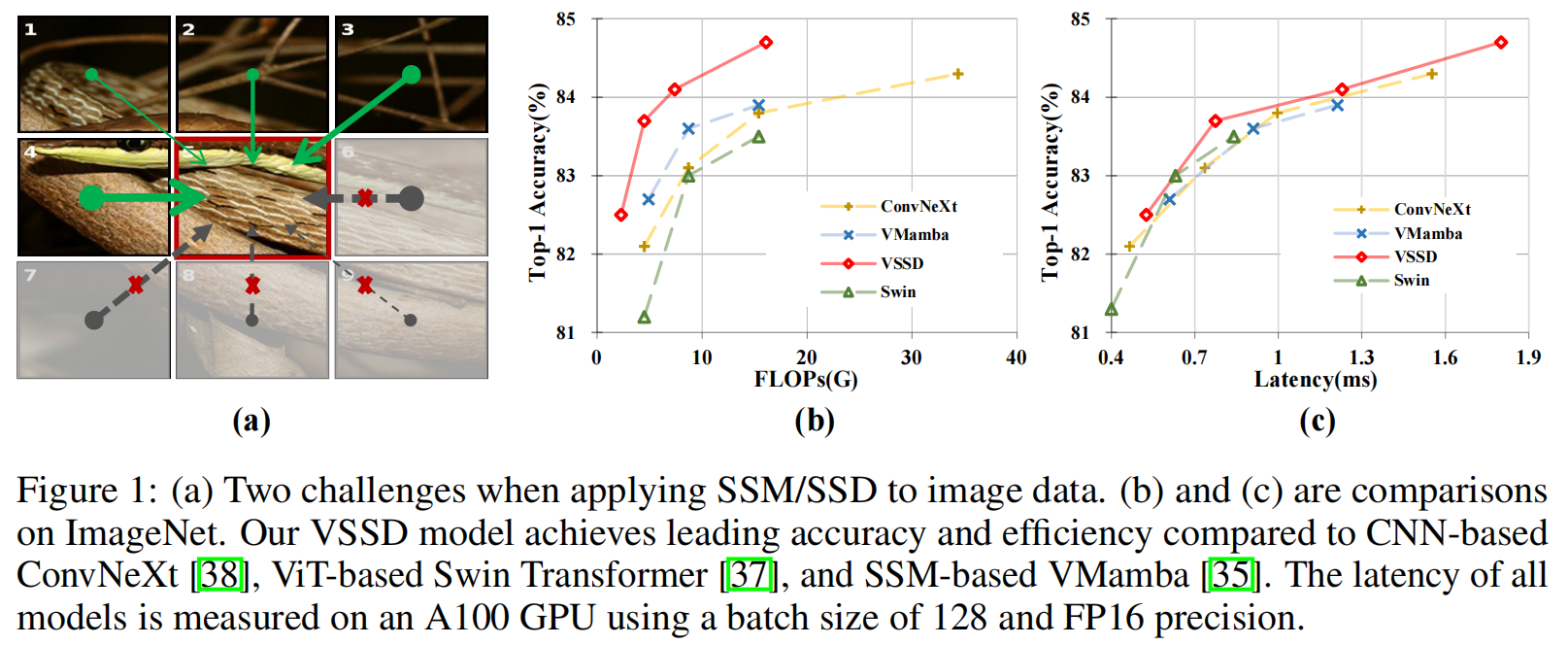
視覺 Transformer 雖憑借全局感受野和強大建模能力在計算機視覺領域取得成功，但其自注意力機制的二次計算復雜度限制了長序列處理能力。狀態空間模型（SSMs）如 Mamba 因線性復雜度成為替代方案，但 SSMs 及改進變體 SSD（State Space Duality）存在固有因果性，與圖像數據的非因果性矛盾，且將 2D 特征圖 flatten 為 1D 序列會破壞空間結構關系。為此，提出VSSD（Visual State Space Duality）模型，通過非因果化 SSD 解決上述問題。

2. 核心方法

2.1 預備知識:mamba-ssm

狀態空間模型:經典的狀態空間模型（SSMs）表示一個連續系統，它將輸入序列 $\in \mathbb{R}^{L}$ 映射到 latent 空間表示 $\in \mathbb{R}^{N}$ ，然后基于該表示預測輸出序列 $\in \mathbb{R}^{L}$ 。從數學上講，SSM可描述為：
$h′(t)=Ah(t)+Bx(t),y(t)=Ch(t)\begin{equation} h'(t) = A h(t) + B x(t), \quad y(t) = C h(t) \end{equation}$
其中 $\in \mathbb{R}^{N ×N}$ 、 $\in \mathbb{R}^{N ×1}$ 和 $\in \mathbb{R}^{1 ×N}$ 是可學習參數。

離散化:為了使連續狀態空間模型（SSMs）適用于深度學習框架，實現離散化操作至關重要。通過引入時間尺度參數 $Δ∈R\Delta \in \mathbb{R}$ 并采用廣泛使用的零階保持（ZOH）作為離散化規則，可以推導出A和B的離散化版本（分別表示為 $A￣\overline{A}$ 和 $B￣\overline{B}$ ），據此，式1可重寫為離散形式：
$h(t)=A￣h(t?1)+B￣x(t),y(t)=Ch(t),where?A￣=eΔA,B￣=(ΔA)?1(eΔA?I)ΔB≈ΔB\begin{equation} \begin{aligned} h(t) &= \overline{A} h(t-1) + \overline{B} x(t), \quad y(t) = C h(t), \\ \text{where } \overline{A} &= e^{\Delta A}, \quad \overline{B} = (\Delta A)^{-1} \left(e^{\Delta A} - I\right) \Delta B \approx \Delta B \end{aligned} \end{equation}$
離散化的詳細推導可見這篇文章
其中 $I$ 表示單位矩陣。之后，式2的過程可以通過全局卷積的方式實現：
$y=x⊙K￣,K￣=(CB￣,CA￣B￣,…,CA￣L?1B￣)\begin{equation} y = x \odot \overline{K}, \quad \overline{K} = \left(C \overline{B},\; C \overline{A} \overline{B},\; \dots,\; C \overline{A}^{L-1} \overline{B}\right) \end{equation}$
該式直接迭代帶入即可得到
其中 $\in \mathbb{R}^{1 × L}$ 是輸入序列， $K￣∈RL×1\overline{K} \in \mathbb{R}^{L × 1}$ 是卷積核。

選擇性狀態空間模型：Mamba引入的選擇性狀態空間 $S 6$ 機制使參數 $B￣\overline{B}$ 、 $C￣\overline{C}$ 和 $Δ$ 依賴于輸入，從而提升了基于SSM的模型的性能。在使 $B￣\overline{B}$ 、 $C￣\overline{C}$ 和 $Δ$ 依賴于輸入后，式3中的全局卷積核可重寫為：
$K￣=(CLB￣L,CLA￣L?1B￣L?1,…,CL∏i=1L?1A￣iB￣1)\begin{equation} \overline{K} = \left( C_{L} \overline{B}_{L},\; C_{L} \overline{A}_{L-1} \overline{B}_{L-1},\; \dots,\; C_{L} \prod_{i=1}^{L-1} \overline{A}_{i} \overline{B}_{1} \right) \end{equation}$
這種修改解決了先前 SSM 模型 [16, 13] 固有的線性時不變（LTI）特性的局限性，從而提升了 SSMs 的適應性和性能。

2.2 非因果狀態空間對偶性

最近，Mamba2引入了狀態空間對偶性（SSD），并將矩陣 $A$ 簡化為標量。這種選擇性狀態空間模型（SSMs）的特殊情況可通過線性和二次兩種形式實現。不失一般性，選擇性狀態空間模型的矩陣變換形式表示如下：
$y(t)=∑i=1tCt?At:i+1Bix(i),其中?At:i=∏k=itAk,y=SSM(A,B,C)(x)=Fx,其中?Fji=Cj?Aj:iBi\begin{equation} \begin{aligned} y(t) &= \sum_{i=1}^{t} C_t^{\top} A_{t:i+1} B_i \, x(i), \quad \text{其中 } A_{t:i} = \prod_{k=i}^{t} A_k, \\ y &= \text{SSM}(A, B, C)(x) = F x, \quad \text{其中 } F_{ji} = C_j^{\top} A_{j:i} B_i \end{aligned} \end{equation}$

當 $A_{i}$ 簡化為標量 時，式5的二次形式可重新表述為：
$y=Fx=M?(CTB)x,其中Mij={Ai+1×?×Aji>j1i=j0i<j,\begin{equation} y=F x=M \cdot\left(C^{T} B\right) x, 其中M_{i j}=\left\{\begin{array}{ll} A_{i+1} × \cdots × A_{j} & i>j \\ 1 & i=j \\ 0 & i<j, \end{array} \quad\right. \end{equation}$
其線性形式表示為：
$h(t)=Ath(t?1)+Btx(t),y(t)=Cth(t).\begin{equation} h(t)=A_{t} h(t-1)+B_{t} x(t), y(t)=C_{t} h(t) . \end{equation}$

為使SSMs適應圖像數據，需先將二維特征圖展平為一維token序列，再對其進行順序處理。由于SSMs的因果特性（每個token只能訪問之前的token），信息傳播本質上是單向的。這種因果特性在處理非因果圖像數據時會導致性能不佳，這一發現已得到先前研究的證實。此外，將二維特征圖展平為一維序列會破壞其內在的結構信息。例如，在二維圖中相鄰的token在一維序列中可能相距甚遠，從而導致視覺任務性能下降。由于SSD是SSMs的一種變體，將SSD應用于視覺任務會遇到與SSMs類似的挑戰：

挑戰1：模型的因果特性限制了信息流動，使后續token無法影響先前的token。
挑戰2：在處理過程中，將二維特征圖展平為一維序列會破壞補丁之間固有的結構關系。

在將因果SSD應用于非因果圖像數據的背景下，回顧SSD的線性公式很有啟發性。在式7中，標量 $A_{t}$ 調節先前隱藏狀態 $h (t ? 1)$ 和當前時間步信息的影響。換句話說，當前隱藏狀態 $h (t)$ 可視為先前隱藏狀態和當前輸入的線性組合，分別由 $A_{t}$ 和1加權。因此，如果我們忽略這兩項的大小，只保留它們的相對權重，式7可重寫為：
$h(t)=h(t?1)+1AtBtx(t)=∑i=1t1AiBix(i).\begin{equation} h(t)=h(t-1)+\frac{1}{A_{t}} B_{t} x(t)=\sum_{i=1}^{t} \frac{1}{A_{i}} B_{i} x(i) . \end{equation}$

在這種情況下，特定token對當前隱藏狀態的貢獻可由其自身直接通過 $1Ai\frac{1}{A_{i}}$ 確定，而非通過多個系數的累積乘法。由于每個token的貢獻具有自參考性，挑戰2僅得到部分解決，因為由于挑戰1中討論的問題，當前token只能訪問一部分token。

為解決挑戰1，先前基于SSM的視覺模型經常采用多掃描路徑。具體而言，在ViM中，對token序列進行正向和反向掃描，使每個token能夠訪問全局信息。盡管這些多掃描方法減輕了SSMs的因果特性，但它們并未解決挑戰2，因為SSMs的長程衰減特性仍局限于一維形式，并未擴展到二維。為了能夠獲取全局信息，從而適應非因果圖像數據，我們也從雙向掃描策略入手。并且我們證明，正向和反向掃描的結果可以整合起來，以同時有效解決上述兩個挑戰。令 $H_{i}$ 表示雙向掃描方法中第 $i$ 個token的隱藏狀態，由此我們可以很容易地得出：
$Hi=∑j=1i1AjZj+∑j=?L?i1A?jZ?j=∑j=1L1AjZj+1AiZi,其中Zj=Bjx(j).\begin{equation} H_{i}=\sum_{j=1}^{i} \frac{1}{A_{j}} Z_{j}+\sum_{j=-L}^{-i} \frac{1}{A_{-j}} Z_{-j}=\sum_{j=1}^{L} \frac{1}{A_{j}} Z_{j}+\frac{1}{A_{i}} Z_{i}, 其中Z_{j}=B_{j} x(j) . \end{equation}$

如果我們將式中的 $1AiZi\frac{1}{A_{i}} Z_{i}$ 視為偏置并忽略它，式9可進一步簡化，導致所有token共享相同的隱藏狀態 $H=∑j=1L1AjZjH=\sum_{j=1}^{L} \frac{1}{A_{j}} Z_{j}$ 。在這種情況下，正向和反向掃描的結果可以無縫結合以建立全局上下文，這實際上等效于移除因果掩碼并轉換為非因果形式。因此，與因果特性相關的第一個挑戰得到了解決。盡管上述結果來自雙向掃描方法，但顯然在這種非因果形式中，不同的掃描路徑會產生一致的結果。換句話說，無需設計特定的掃描路徑來捕獲全局信息。此外，如式9所示，不同token對當前隱藏狀態的貢獻不再與其空間距離相關。因此，將展平的二維特征圖處理為一維序列不再會損害原始的結構關系。這樣，第二個挑戰也得到了解決。此外，由于整個計算過程可以并行進行，而不必依賴于先前SSMs所需的循環計算方法，訓練和推理速度得到了提升。在修改了隱藏狀態空間的迭代規則之后，我們按照Mamba2框架，更新了線性形式中相應的張量收縮算法或愛因斯坦求和符號：
$Z=contract(LD,LN→LND)(X,B)H=contract(LL,LDN→ND)(M,Z)Y=contract(LN,ND→LD)(C,H)\begin{equation} \begin{aligned} Z & =contract(LD, LN \to LND)(X, B) \\ H & =contract(LL, LDN \to ND)(M, Z) \\ Y & =contract(LN, ND \to LD)(C, H) \end{aligned} \end{equation}$
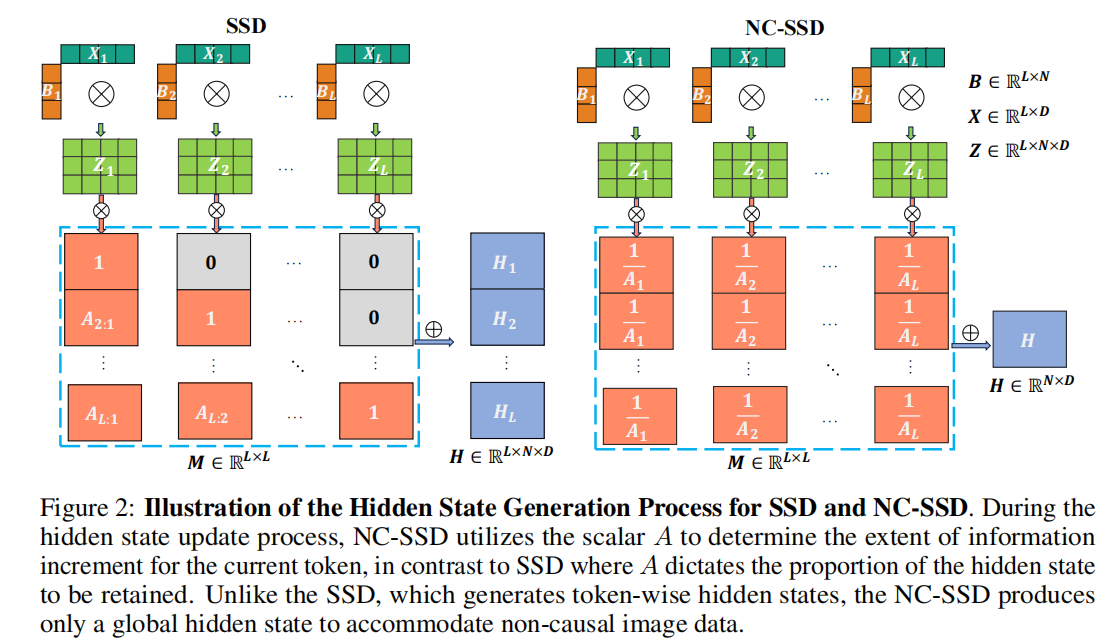
在這里插入圖片描述

該算法包括三個步驟：第一步使用 $B$ 擴展輸入 $x$ ，第二步展開標量SSM遞歸以創建全局隱藏狀態 $H$ ，最后一步將隱藏狀態 $H$ 與 $C$ 收縮。為清晰起見，圖2展示了SSD和NC-SSD的前兩個步驟。與普通SSD相比，雖然第一步的操作保持不變，但在非因果模式下，隱藏狀態 $H$ 中的序列長度維度被消除，因為所有token共享相同的隱藏狀態。在最后一步中，輸出 $Y$ 通過 $C$ 和 $H$ 的矩陣乘法產生。由于 $Mi,j=1AjM_{i, j}=\frac{1}{A_{j}}$ ，通過消除矩陣 $M$ 的第一維，可將其簡化為向量 $\in \mathbb{R}^{L}$ 。在這種情況下，將 $m$ 與 $X$ 或 $B$ 集成可以進一步將式10的變換簡化為：
$Y=C(BT(X?m))\begin{equation} Y=C\left(B^{T}(X \cdot m)\right) \end{equation}$

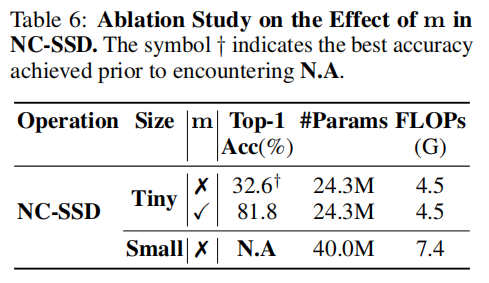
這可以被視為線性注意力的一種變體。然而，值得注意的是，正如 $A$ 在Mamba2中起著重要作用一樣，向量 $m$ 也至關重要，這在我們的消融研究中得到了證明。在實踐中，我們直接使用學習到的 $A$ 而不是 $1A\frac{1}{A}$ ，因為它們具有相同的值范圍。為了更直觀地理解式10中 $m$ 的作用，我們將不同頭的 $m$ 的平均值可視化，如圖3所示。主要來看， $m$ 關注前景特征，使模型能夠優先處理對任務至關重要的元素。

2.3 視覺狀態空間對偶性模型

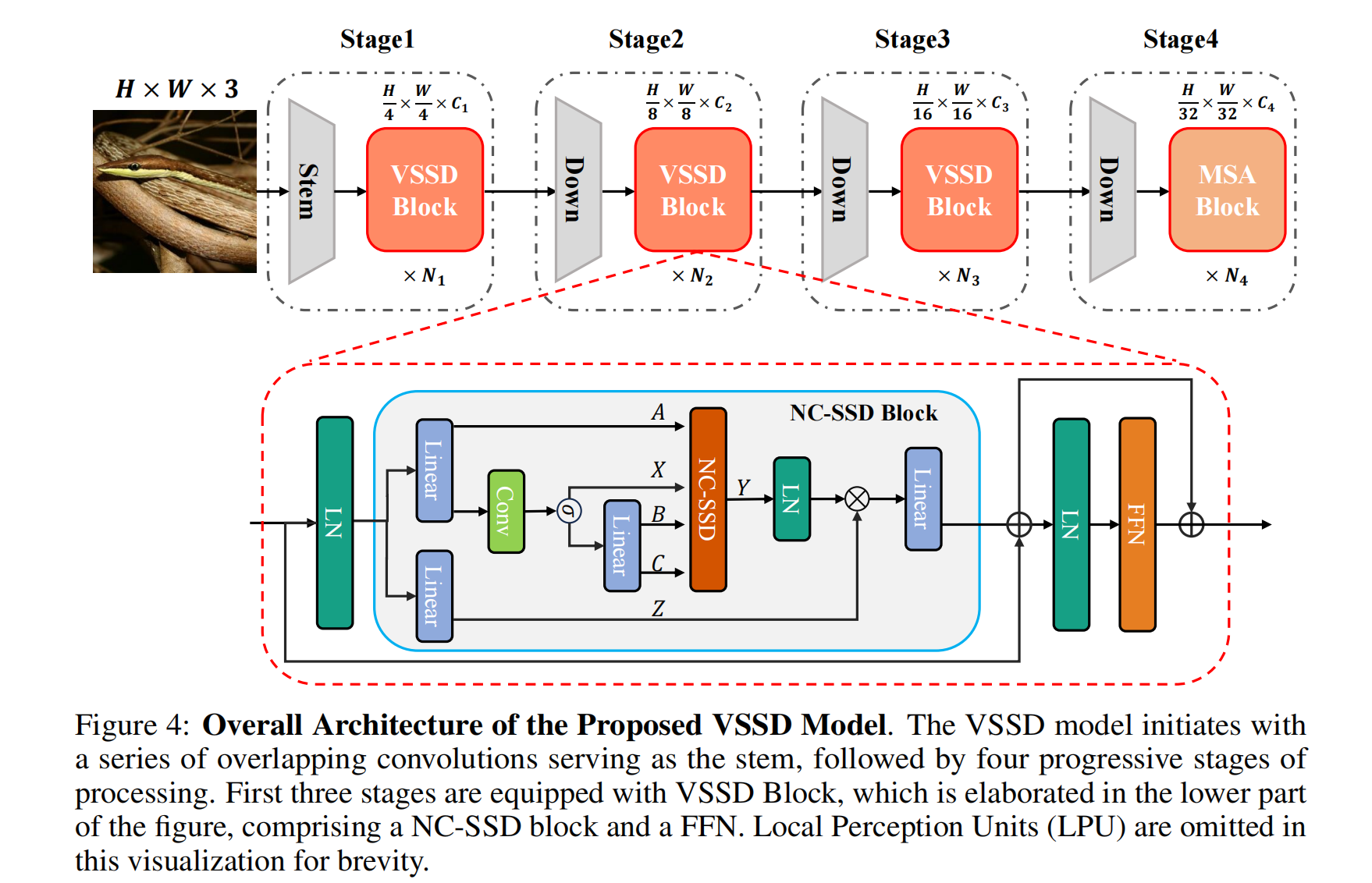
塊設計：為了增強Mamba2中的SSD塊以適應視覺應用，除了僅用NC-SSD替代SSD來開發我們的視覺狀態空間對偶性（VSSD）塊之外，我們還進行了幾項修改。在構建NC-SSD塊時，與先前的視覺mamba研究一致，將因果1D卷積替換為 kernel 大小為3的深度卷積（DWConv）。此外，在NC-SSD塊之后集成了前饋網絡（FFN），以促進跨通道的更好信息交換，并與經典視覺Transformer的既定做法保持一致。此外，在NC-SSD塊和FFN之前加入了局部感知單元（LPU），以增強模型的局部特征感知能力。在不同塊之間還實現了跳躍連接。VSSD塊的架構如圖4下部所示。
與自注意力的混合：Mamba2表明，將SSD與標準多頭自注意力（MSA）集成可帶來額外的改進。同樣，我們的模型也融入了自注意力。然而，與Mamba2在整個網絡中均勻分布自注意力不同，我們僅在最后一個階段用自注意力模塊戰略性地替換NC-SSD塊。這種修改利用了自注意力在處理視覺任務中高級特征方面的強大能力。
重疊下采樣層：由于分層視覺Transformer和視覺狀態空間模型主要采用非重疊卷積進行下采樣，最近的研究表明，重疊下采樣卷積可以引入有益的歸納偏置。因此，我們在模型中采用了重疊卷積，采用的方式與MLLA相同。為了保持參數數量和計算FLOPs相當，我們相應地調整了模型的深度。
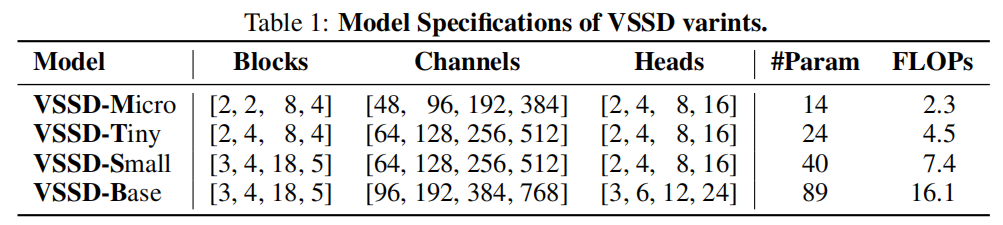
整體架構：我們根據上述方法開發了VSSD模型，其架構如圖4所示。借鑒先前研究中已建立的視覺骨干網絡的設計原則，我們的VSSD模型分為四個分層階段。前三個階段采用VSSD塊，而最后一個階段集成了MSA塊。VSSD變體的詳細架構如表1所示。

3. 實驗結果

3.1 圖像分類任務

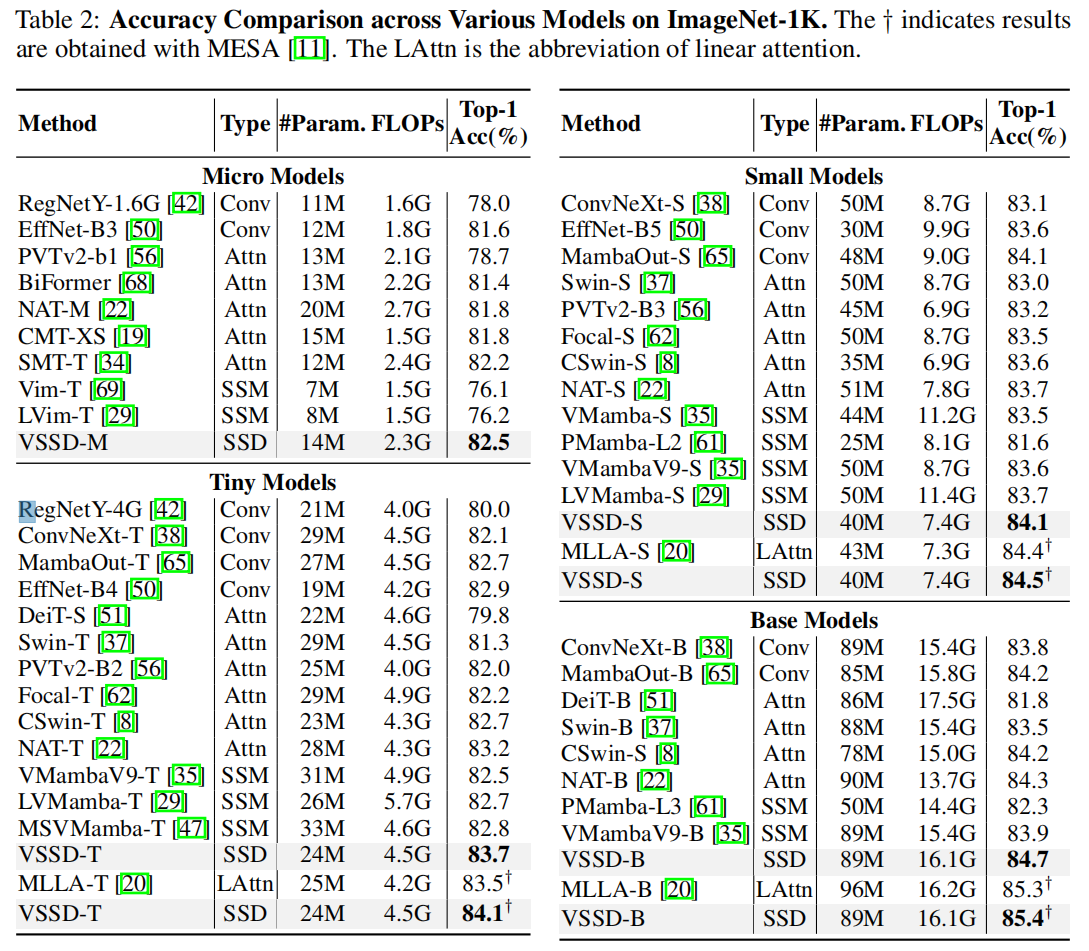
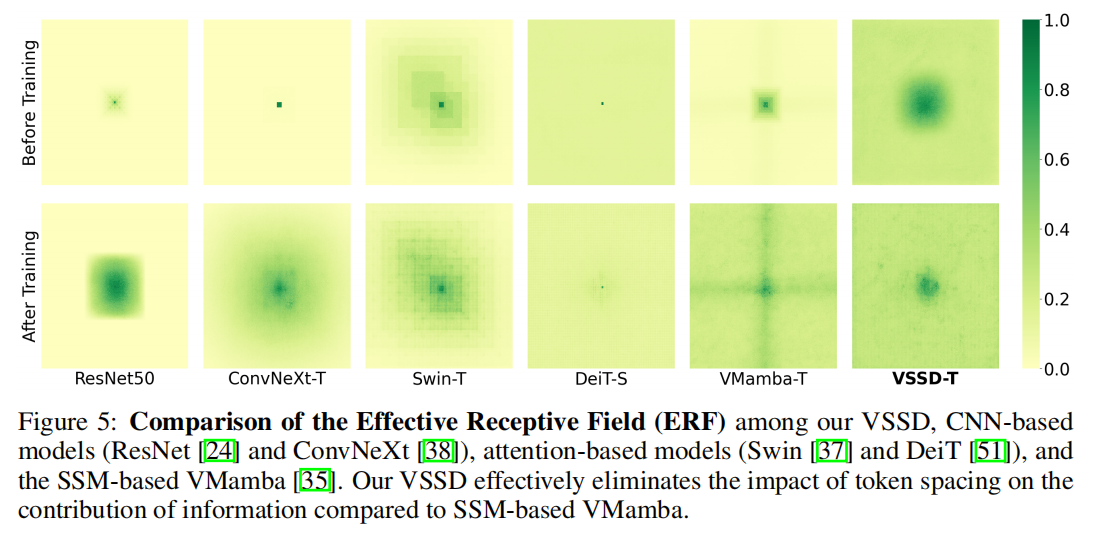
3.2 目標檢測任務

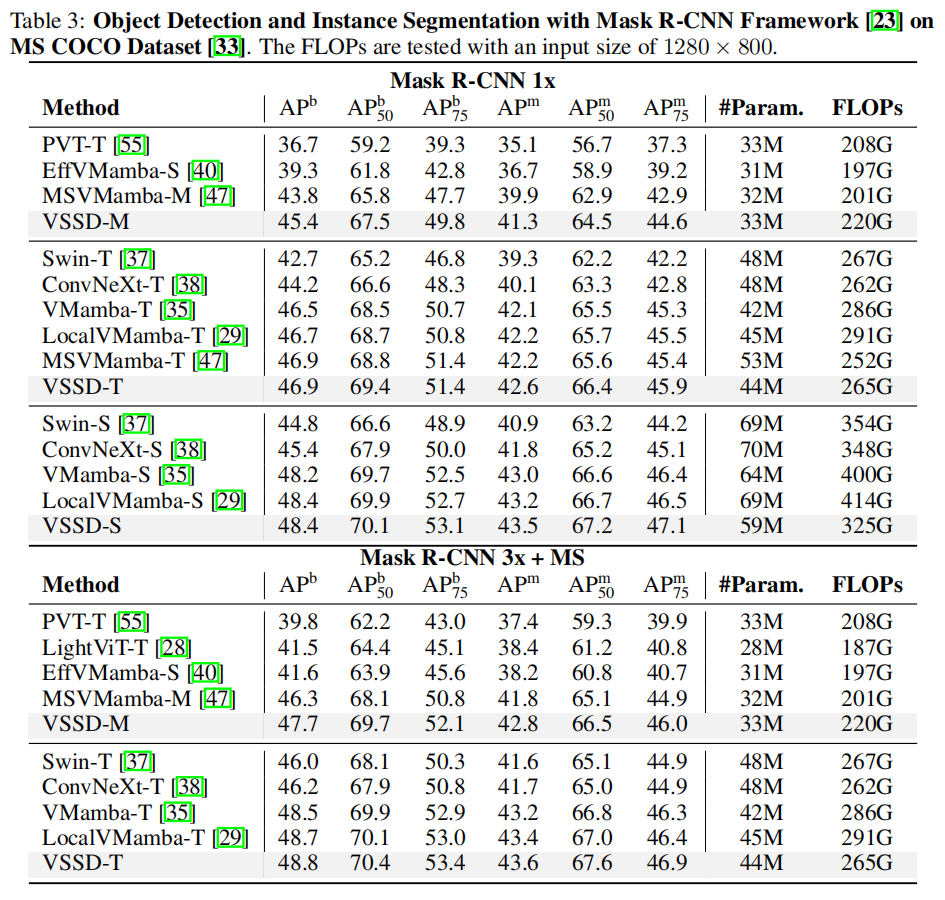
3.3 語義分割任務

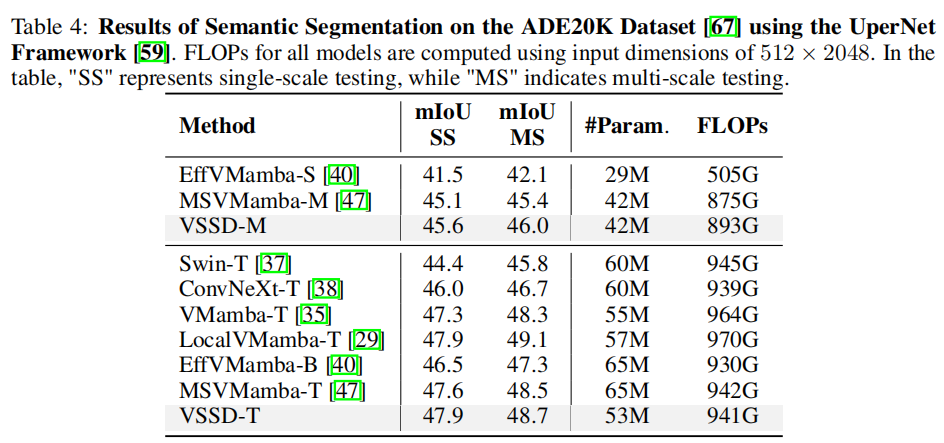
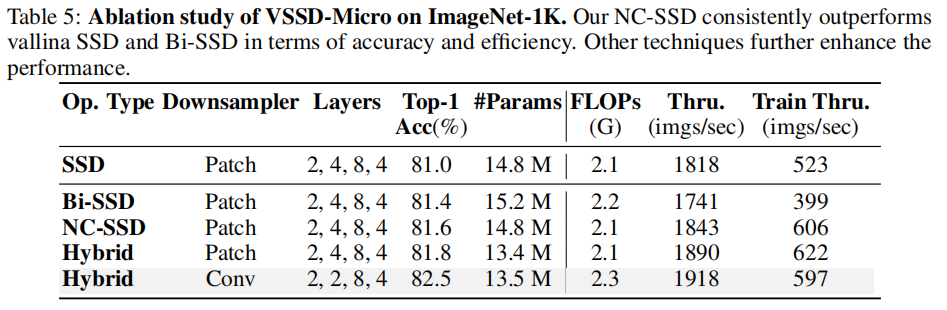
3.4 消融實驗

4.局限性與結論

4.1 局限性

下游任務性能提升有限：盡管 VSSD 在 ImageNet-1K 圖像分類任務中優于其他基于 SSM 的模型，但在下游任務（如目標檢測、語義分割）上，與其他 SSM 模型相比，性能提升幅度較小。
與頂尖 Transformer 變體存在差距：相較于最先進的視覺 Transformer 變體（如 RMT、Dat++ 等），VSSD 在下游任務上的性能仍有顯著差距。
缺乏大規模驗證：未在更大規模模型或數據集（如 ImageNet-22K）上進行實驗，其可擴展性有待進一步探索。

4.2 結論

NC-SSD 的有效性：通過重新定義狀態空間對偶性（SSD）中矩陣 A 的作用并移除因果掩碼，提出的非因果 SSD（NC-SSD）成功將 SSD 轉換為非因果模式，保留了全局感受野和線性復雜度的優勢，同時提升了訓練與推理效率
VSSD 模型的優越性：結合 NC-SSD、混合自注意力機制和重疊下采樣等技術，VSSD 在圖像分類、目標檢測、語義分割等多個基準測試中，與現有 CNN、Transformer 和 SSM-based 模型相比，在相似參數和計算成本下實現了更優或相當的性能。
ERF 優勢：如圖 5 所示，VSSD 有效消除了 token 間距對信息貢獻的影響（相較于 SSM-based 的 VMamba），能更均衡地利用不同位置的信息，更好地保留圖像全局結構關系，這是其在視覺任務中表現優異的重要原因。