機器學習筆記(四)——聚類算法KNN、Kmeans、Dbscan

寫在前面：

寫本系列(自用)的目的是回顧已經學過的知識、記錄新學習的知識或是記錄心得理解，方便自己以后快速復習，減少遺忘。概念部分大部分來自于機器學習菜鳥教程，公式部分也會參考機器學習書籍、阿里云天池。機器學習如果只啃概念始終學不牢，因此我打算概念與代碼結合。

Part 2 機器學習算法

五、KNN

1、KNN的基本原理

KNN，也叫K近鄰算法，是一種簡單且常用的分類和回歸算法。它是監督學習的一種，核心思想是通過計算待分類樣本與訓練集中各個樣本的距離，找到距離最近的 K 個樣本，然后根據這 K 個樣本的類別或值來預測待分類樣本的類別或值。

現在舉一個例子，示例中的圖片來自b站up小萌Annie的K近鄰算法視頻：

假設有兩種狼群，狼群A和狼群B。其中，狼群A的腳印用圖中綠色的圓圈來表示，狼群B的腳印用圖中綠色的正方形來表示。現在給出一個不知道類別的腳印(圖中黑色爪印)，問這個腳印是狼群A留下的還是狼群B留下的。解決這個問題可以使用KNN算法。

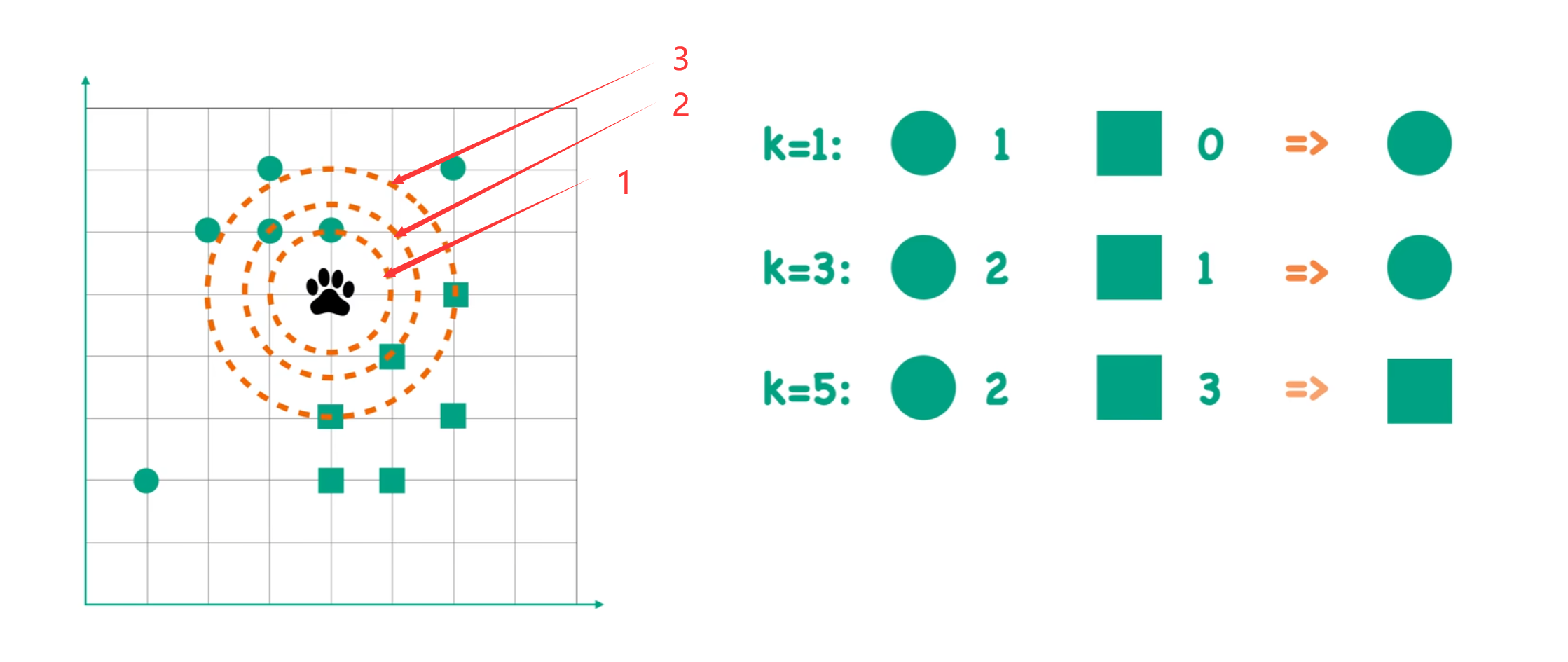
假設我們設置KNN的距離超參數k = 1。也就是說，以待分類樣本(黑色爪印)為圓心，k=1為半徑畫圓，看圓內哪種腳印數量多。例如圖中，當k = 1時，圓圈的數量為1，方形的數量為0，因此我們判斷黑色腳印是圓形，即待分類樣本屬于狼群A。

同理，k = 3時，圓圈的數量為2，方形的數量為1，因此我們判斷黑色腳印是圓形，即待分類樣本屬于狼群A。

k = 5時，圓圈的數量為2，方形的數量為3，因此我們判斷黑色腳印是方形，即待分類樣本屬于狼群B。

這就是KNN算法解決分類問題的案例(解決回歸問題就是取k個最近鄰點的平均值)。那么需要解決的問題就是KNN算法的距離如何度量。

2、距離度量(可以只了解歐氏距離)

這里shun'dai常用的距離度量方法如下：

(1)歐式距離

歐式距離是KNN最常用的距離度量，計算n維空間中兩點x、y的直線距離的公式為：

$d(x, y)=\sqrt{\sum_{i=1}^{n} (x_i-y_i)^2}$

(2)曼哈頓距離

計算n維空間中兩點在網格狀空間中的最短路徑距離，如城市街區距離:

$d(x, y)=\sum_{i=1}^{n} |x_i-y_i|$

(3)切比雪夫距離?

表示兩點在各維度上差值的最大值：

$d(x, y)=max_i|x_i-y_i|$

(4)閔可夫斯基距離

是歐氏距離和曼哈頓距離的廣義形式：

$d(x, y)=(\sum_{i=1}^{n} |x_i-y_i|^p)^{\frac{1}{p}}$

當p=1時為曼哈頓距離，p=2時是歐式距離，p趨于無窮時等價于切比雪夫距離。?

(5)余弦相似度?

衡量兩個n維向量方向的相似性：

$d(x, y)=1-\frac{x*y}{||x||*||y||}=1-\frac{\sum_{i=1}^{n}x_iy_i}{sqrt{\sum_{i=1}^{n}x_i^2}*sqrt{\sum_{i=1}^{n}y_i^2}}$

這里，分子是兩個向量x、y的點積；分母是向量模長的乘積。

(6)漢明距離

兩個等長字符串對應位置不同字符的數量，常用于分類變量：

d(x, y) = 不同位置的數量

(7)馬氏距離

考慮數據分布協方差的距離度量，消除特征間的相關性：

$d(x, y)=\sqrt{(x-y)^T S^{-1}(x-y)}$

其中，S是數據的協方差矩陣。

(8)編輯距離

將一個字符串轉換為另一個字符串所需的最少編輯操作次數（插入、刪除、替換）。

在KNN中，距離度量的選擇直接影響算法性能。不同距離函數會導致不同的近鄰定義，從而影響結果，最常用的距離是歐氏距離。

例如，圖像識別，地理坐標分析等常用歐氏距離；文本分類等常用余弦相似度；棋盤游戲可以考慮切比雪夫距離。如果難以抉擇如何選取距離，可以通過交叉驗證比較不同距離函數的性能。

3、KNN步驟總結

KNN算法的步驟可以概括如下：

1、計算距離：計算待分類樣本與訓練集中每個樣本的距離。

2、選擇k個最近鄰樣本。

3、投票或取平均：對于分類問題，K 個最近鄰中出現次數最多的類別即為待分類樣本的類別；對于回歸問題，K 個最近鄰的值的平均值即為待分類樣本的值。

4、KNN的代碼實現

from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score# 加載Iris數據集
iris = datasets.load_iris()
X = iris.data # 只取前兩個特征
y = iris.target# 將數據集拆分為訓練集和測試集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)# 創建KNN模型，設置K值為3
knn = KNeighborsClassifier(n_neighbors=3)
'''
這里是默認使用歐氏距離，也就是：
knn = KNeighborsClassifier(n_neighbors=3, metric='euclidean')
metric就是選擇距離度量方式，'euclidean'是歐式距離
'manhattan'是曼哈頓、'chebyshev'是切比雪夫、'cosine'是余弦、'hamming'是漢明、'mahalanobis'是馬氏距離
metric='minkowski', p=2這樣是參數為2的閔可夫斯基距離
當然，也可以自定義距離函數
寫好函數后將函數傳入，即 metric= 函數名 即可。
'''# 訓練模型
knn.fit(X_train, y_train)# 在測試集上進行預測
y_pred = knn.predict(X_test)# 計算準確率
accuracy = accuracy_score(y_test, y_pred)
print(f"KNN模型的準確率: {accuracy:.4f}")

六、k-means

1、k-means的原理?

k-means算法也是一種經典的無監督學習算法。它的目標是：將n個數據點劃分為k個簇，每個簇由其質心代表，使得所有數據點到其所屬質心的平方和距離最小。

2、算法步驟?

1、初始化：隨機選取k個數據點作為初始的質心；

2、分配：將每個數據點分配到距離最近的質心所在的簇；(這里默認使用且最常使用的是歐式距離，也可以使用其他距離度量方式)

3、更新：重新計算每個簇的質心，質心的計算是對簇內所有數據點的每個維度取平均值。

例如某簇里有三個點：(1,?2)，(3,?4)，(5, 6)，該簇的中心就是(3, 4)。=>((1+3+5)/3,(2+4+6)/3)

4、迭代：重復步驟 2-3，直到質心不再變化或達到最大迭代次數。

3、示例

示例來源于b站up平安喜悅孫瑜的k-means聚類算法講解視頻。

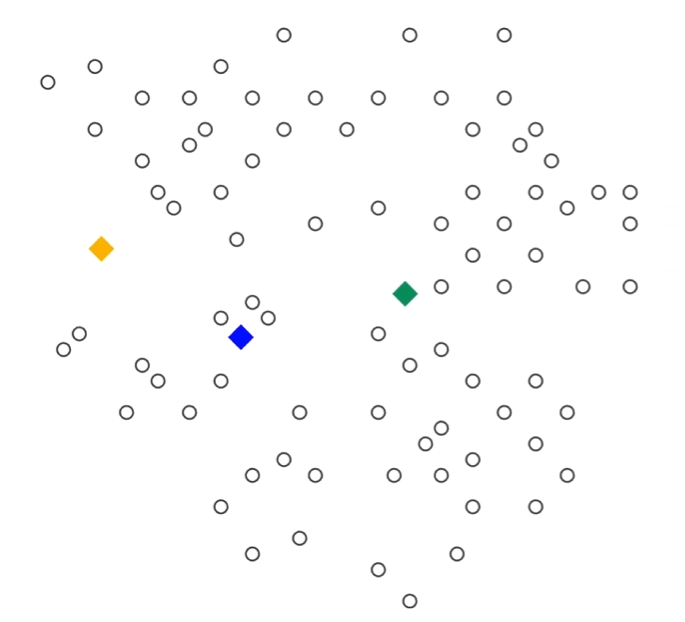
1、初始化三個質心：黃、藍、綠

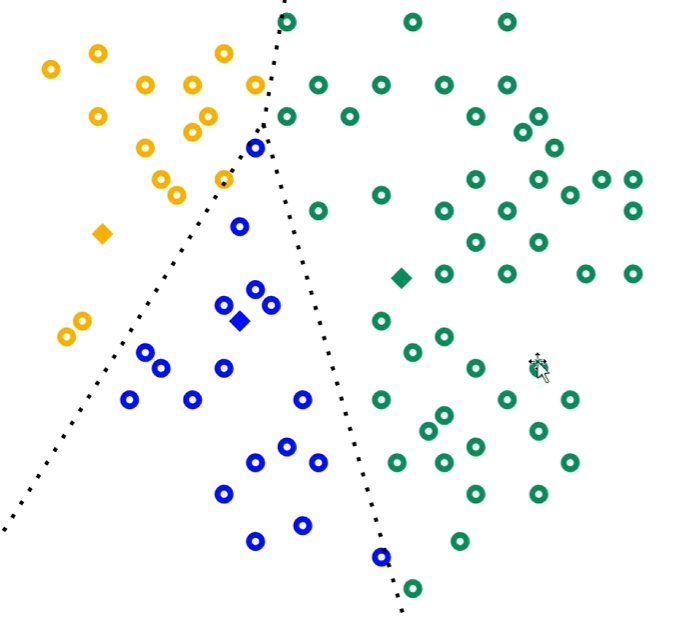
?2、對每個白色的點，分別計算它到這三個質心的距離。離哪個質心近，就把它歸為那一類。每個點均分類完成后如下圖：

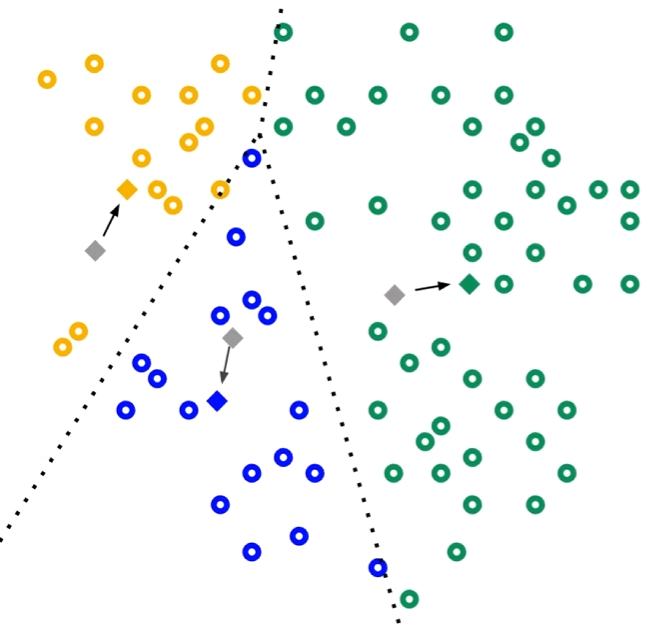
?3、計算出三個類的質心，作為新的簇中心：

4、算出簇中心后，重新計算每個點離三個質心的距離，重新分類；一直循環直到質心不再變化或者達到最大迭代次數。

4、代碼實現

from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt# 生成模擬數據（3個簇）
X, _ = make_blobs(n_samples=300, centers=3, cluster_std=0.60, random_state=42)# 構建 K-means 模型
kmeans = KMeans(n_clusters=3, init='k-means++', max_iter=300, random_state=42)
y_pred = kmeans.fit_predict(X)# 可視化結果
plt.scatter(X[:, 0], X[:, 1], c=y_pred, cmap='viridis')
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], s=300, c='red', marker='X')
plt.title('K-means Clustering')
plt.show()

七、DBSCAN

1、算法原理

DBSCAN是一種基于密度的空間聚類算法，能夠將高密度區域劃分為簇，并將低密度區域識別為噪聲點。DBSCAN中有以下幾個核心概念：

設有n個待聚類點，當前操作點設為p點。

1、ε 鄰域：以點?p?為中心、半徑為?ε?的區域。如下圖所示，p點為中心，?ε =2，黑色圓內即為ε 鄰域。

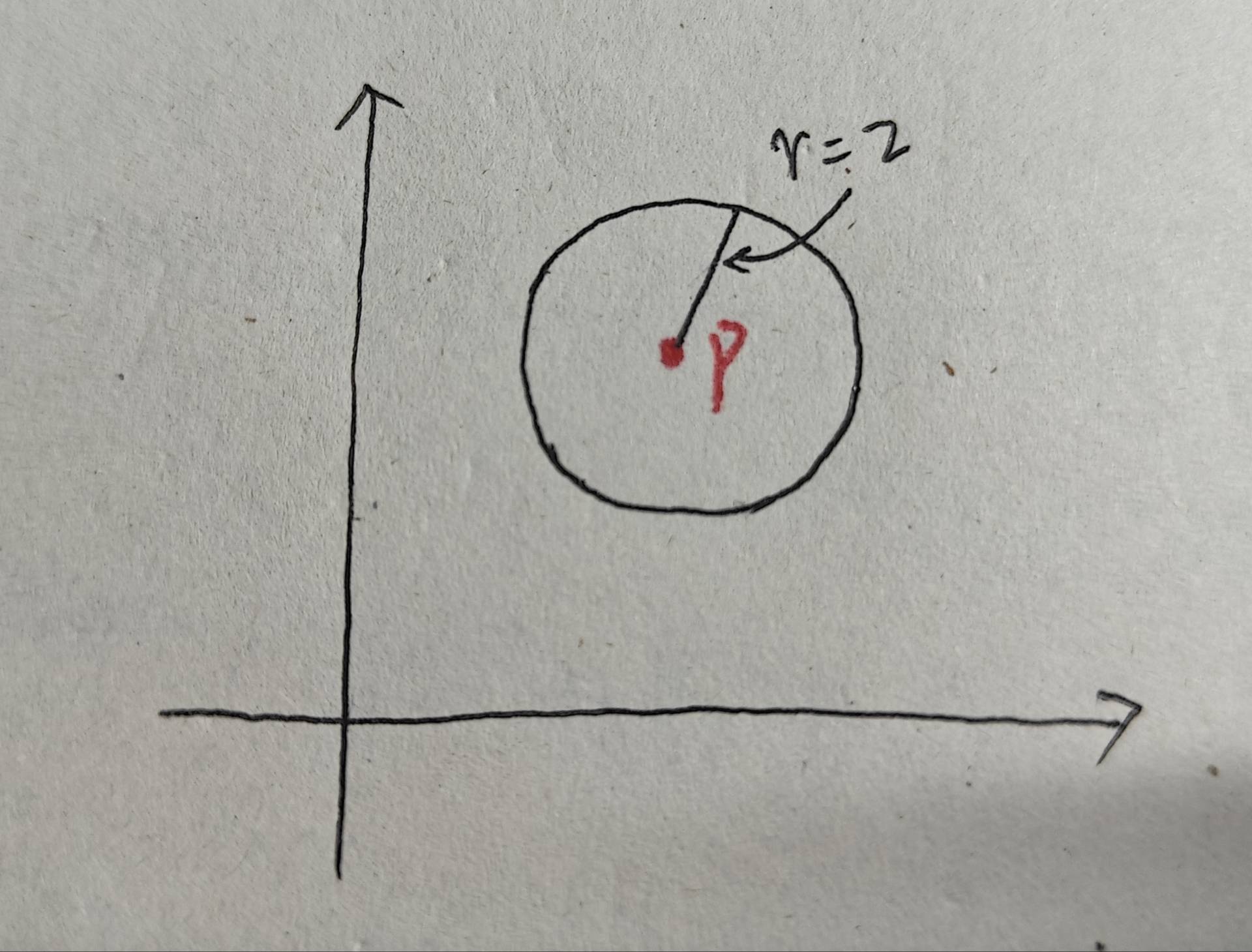
2、MinPts：核心點最小點數，由用戶指定。

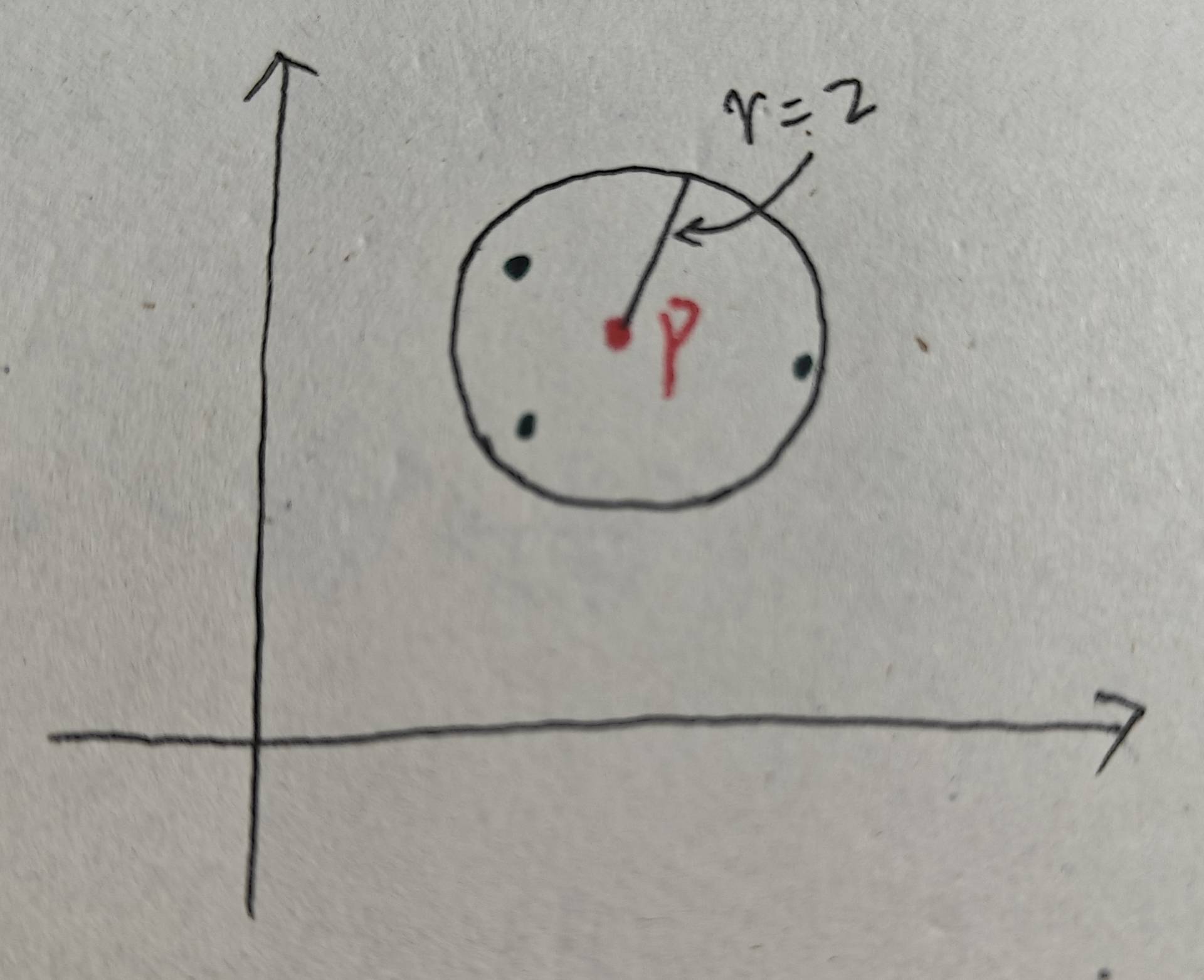
3、核心點：若點?p?的 ε 鄰域內至少包含?MinPts?個點，則?p?是核心點。如下圖所示：設MinPts為4，此時p點的ε 鄰域內恰好有4個點(包含p本身)，則p為核心點：

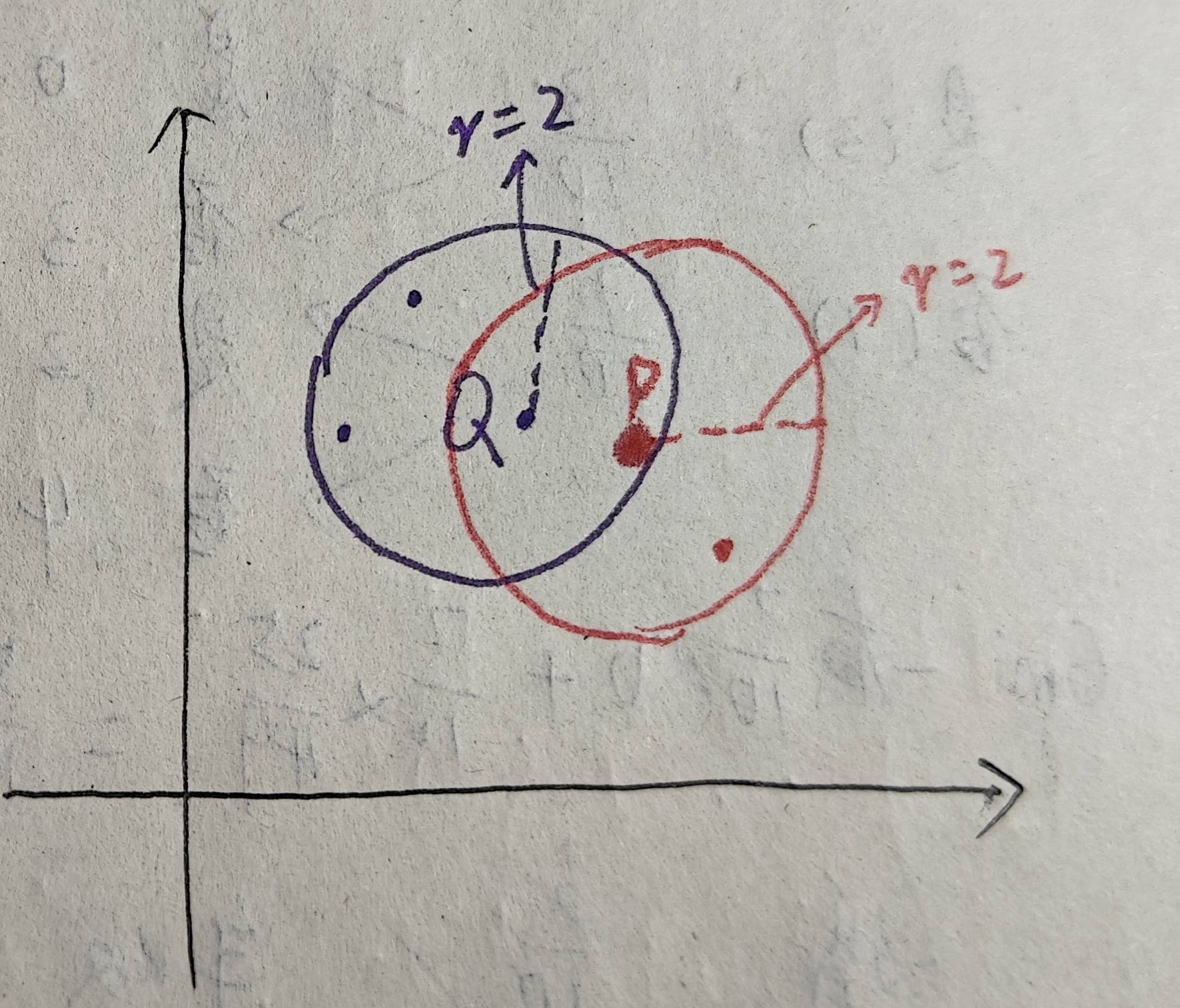
4、邊界點：若點?p?的 ε 鄰域內點的數量少于?MinPts，但它屬于某個核心點的 ε 鄰域，則?p?是邊界點。如圖，設Minpts =? 4，已知核心點Q。如圖，p點領域內只有兩個點，因此p不是核心點，但是p在Q的ε 鄰域內，因此p是邊界點：

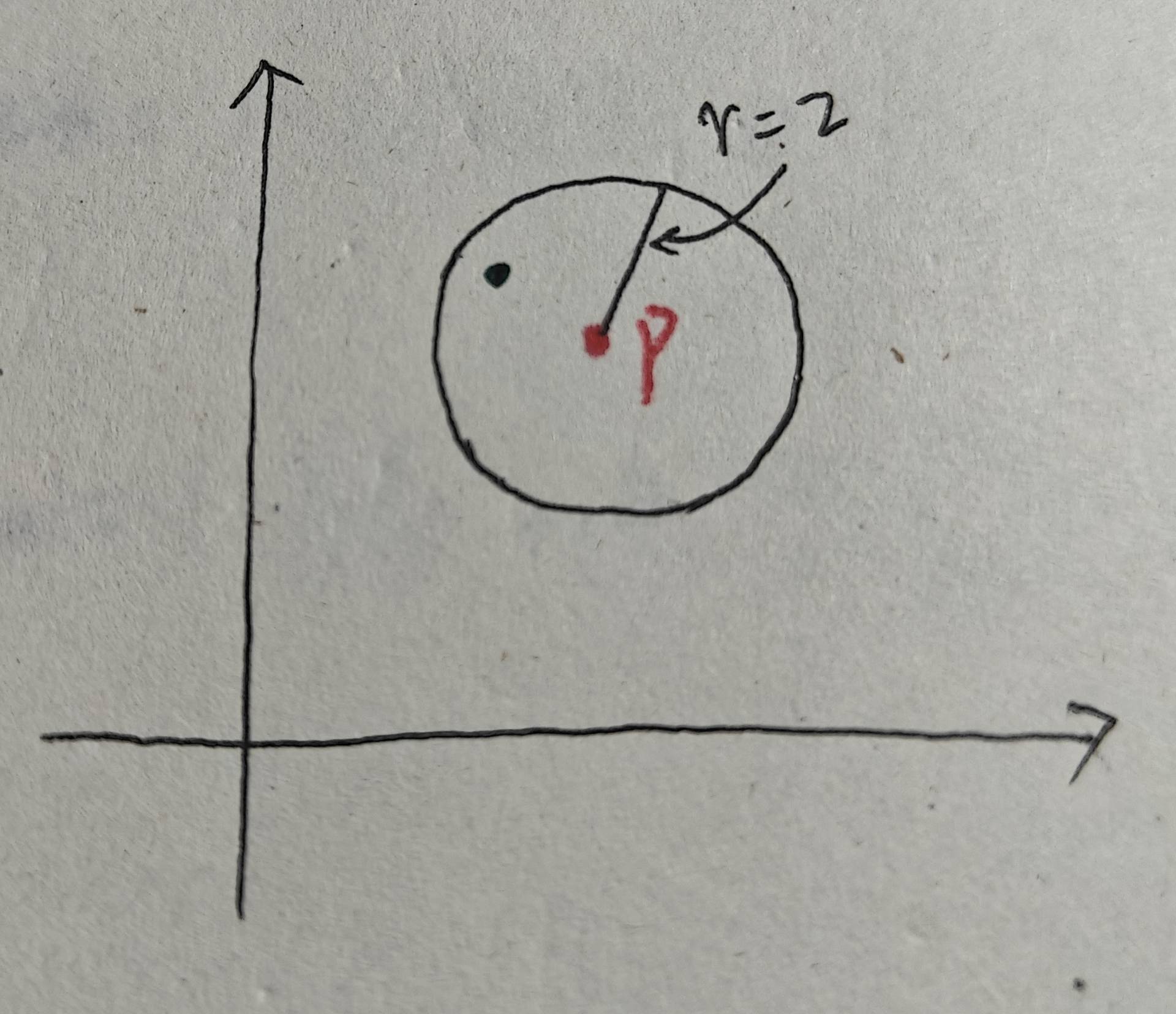
5、噪聲點：既不是核心點也不是邊界點的點。如下圖所示，依然設MinPts = 4，p中只有兩個點，小于MinPts，所以p不是核心點。又因為p也不屬于其他核心點的ε 鄰域領域，p也不是邊界點。因此，p是噪聲點：

6、直接密度可達：若點?q?在核心點?p?的 ε 鄰域內，則稱?q?從?p?直接密度可達。

7、間接密度可達：若q1不在核心點p的ε 鄰域內，q2在核心點p的ε 鄰域內，且q1在q2的ε 鄰域內，那么q1與p間接密度可達。

2、算法流程

1、參數設置：指定ε和?MinPts。

2、遍歷所有的點：

? ??若點?p?是核心點，創建一個新簇，并遞歸地將所有從?p?密度可達(直接+間接)的點加入該簇。

? ??若點?p?是邊界點或噪聲點，暫時標記為未分類。

3、完成分類

3、算法示例

對以下數據點使用DBSCAN算法進行聚類。

這里指定ε = 2， MinPts = 3。

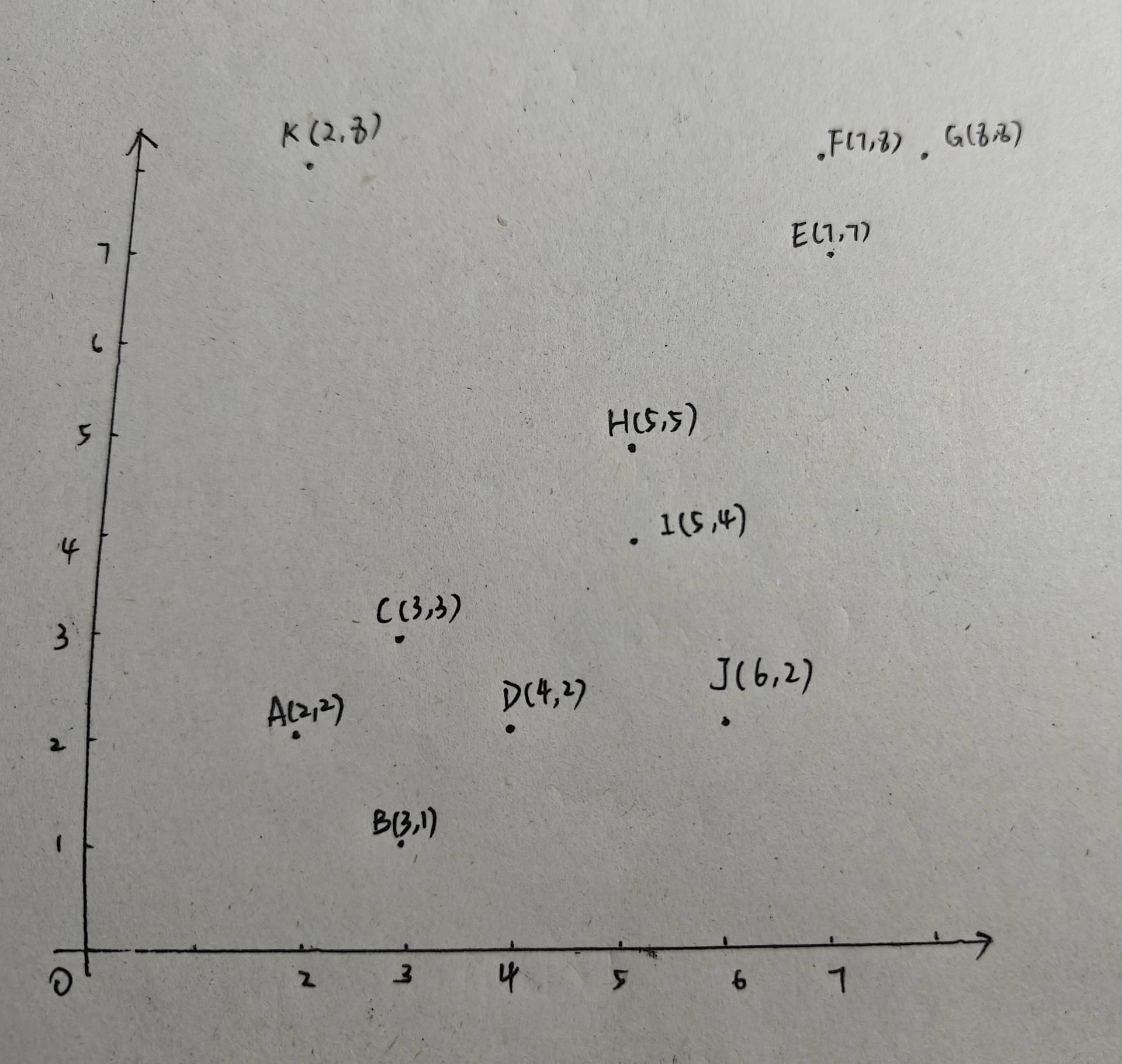
如圖，對點A以2為半徑畫圓，可得A、B、C、D都在圓內，則A為核心點，可得第一個類：{A，B，C，D}。

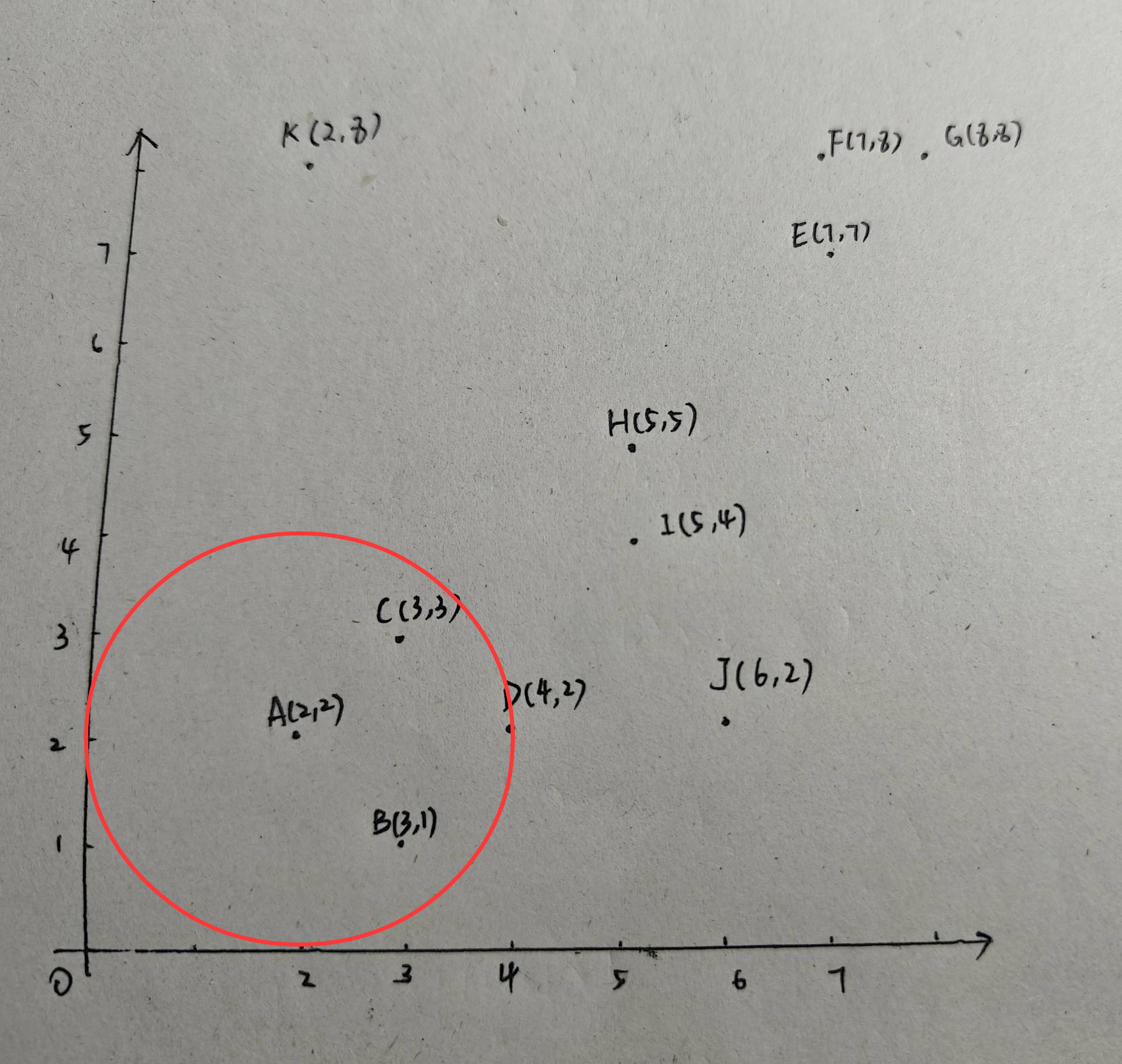
同理對B、C畫圓，B、C都是核心點，由于B、C都在第一個類中了，因此沒有新建類別，并且B、C的鄰域中沒有包含新的點，類別1仍為：{A，B，C，D}。接下來對D以2為半徑畫圓：

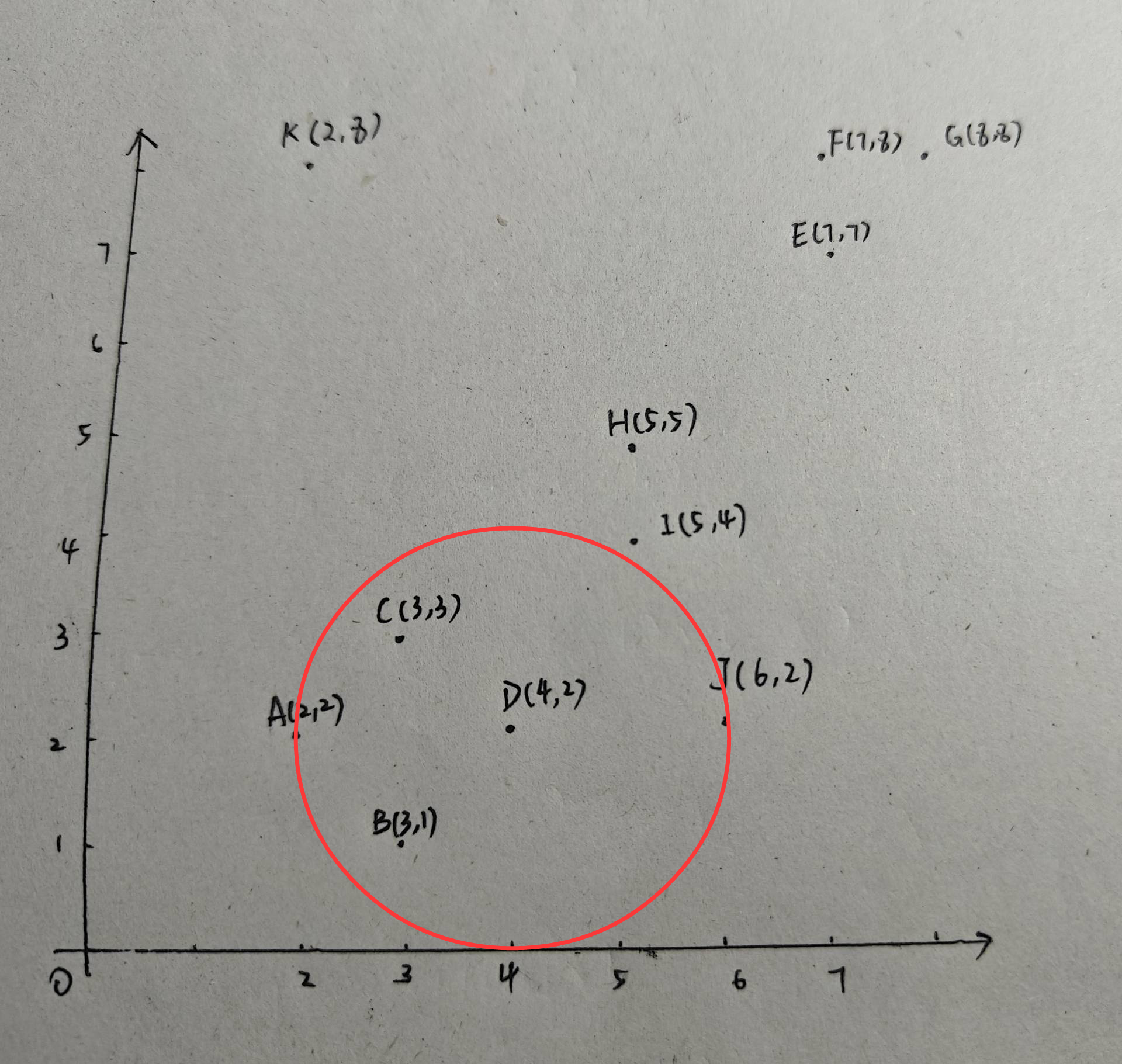
可見，D也是核心點，且D中包含了J，因此類別1進行更新：{A，B，C，D，J}。現在以E為圓心，2為半徑畫圓：

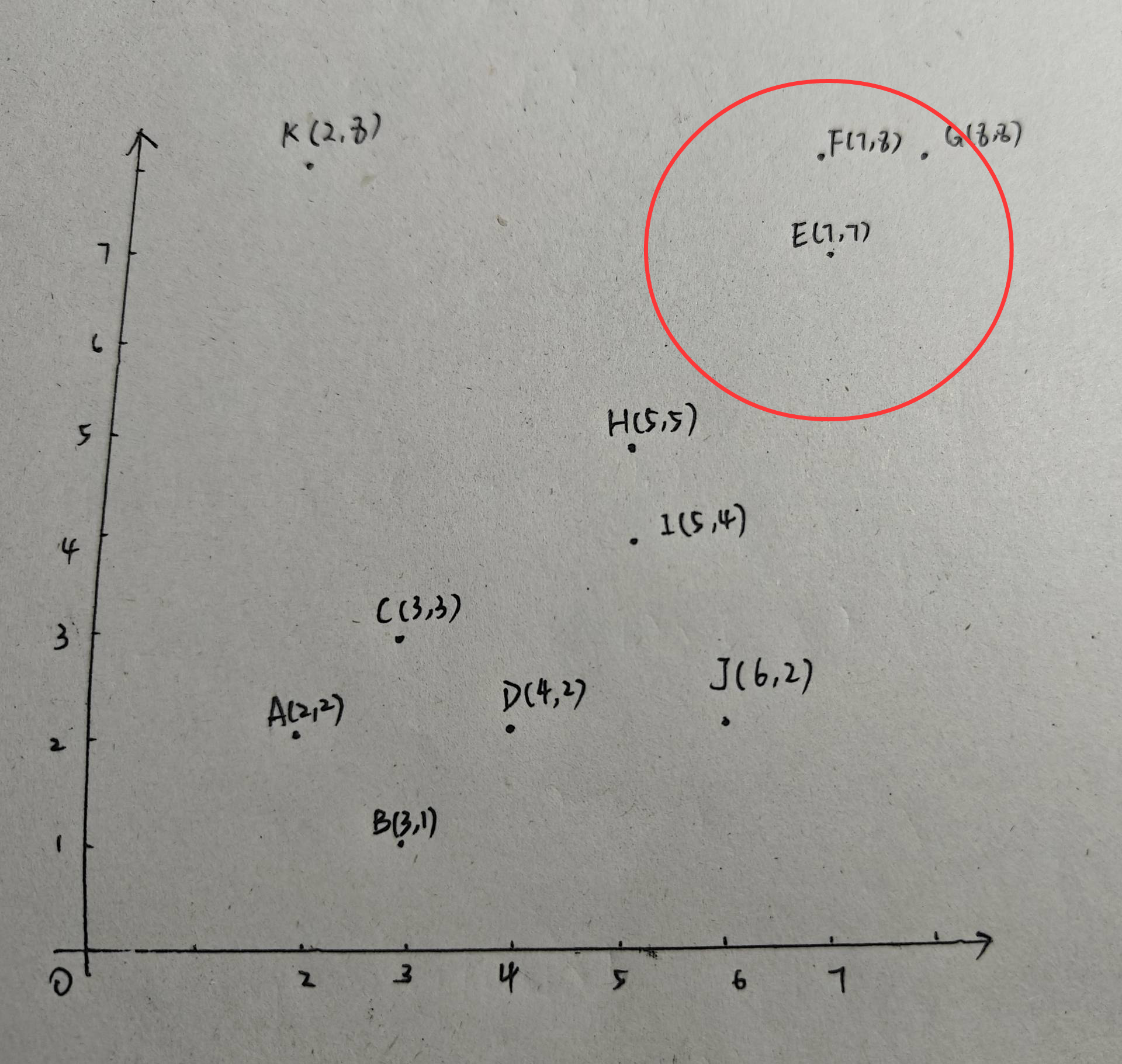
可以看出，E也是核心點，E、F、G都在圓內。由于此時并沒有類別包含E，因此新建一個類2：{E、F、G}。至此，我們已經有兩個類別：{A，B，C，D，J}、{E、F、G}。

同理，對F、G畫圓，F、G都是核心點，由于F、G都在第二個類中了，因此沒有新建類別，并且F、G的鄰域中沒有包含新的點，類別2仍為：E、F、G}。接下來，以點H為半徑，2為圓心畫圓：

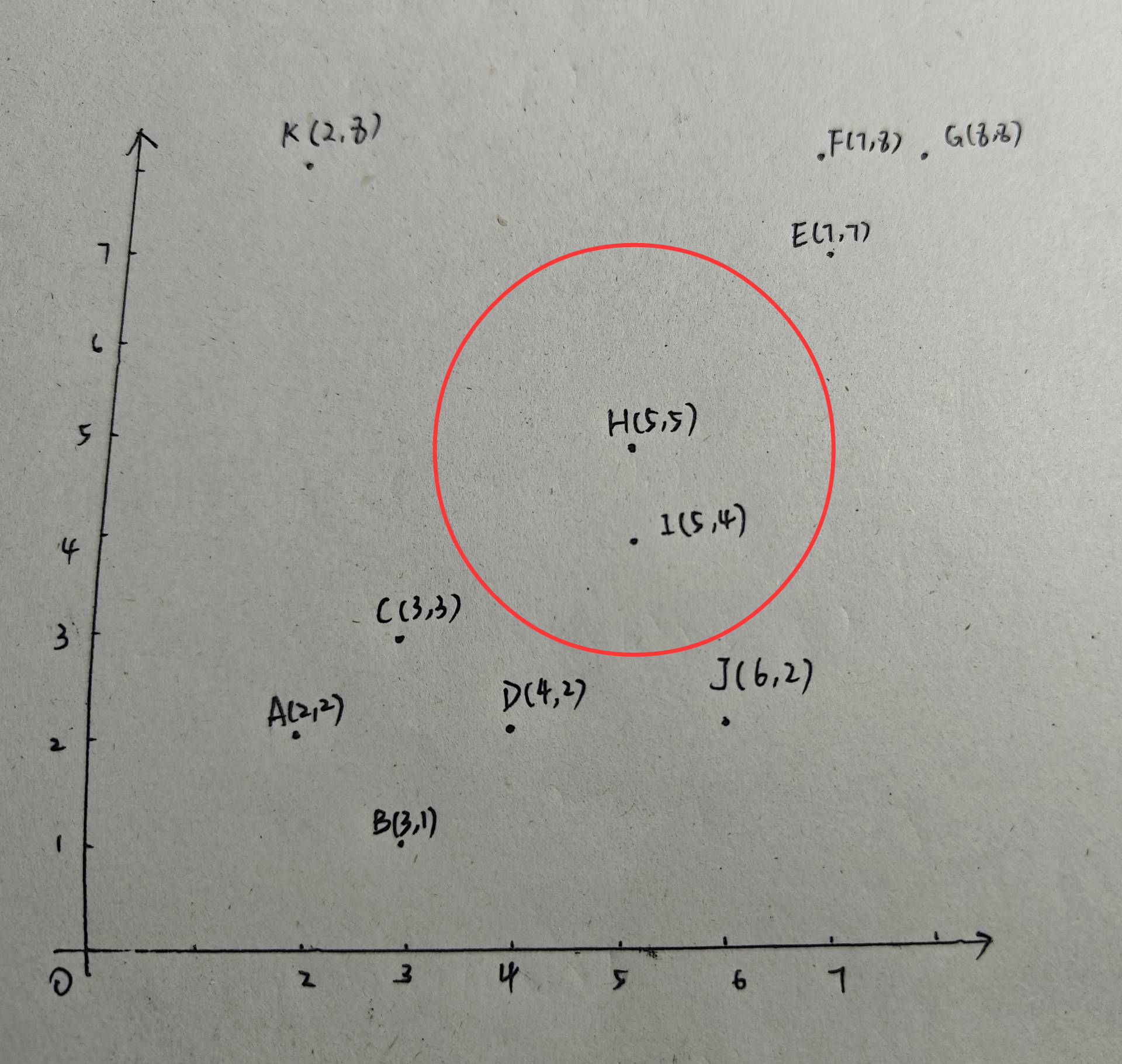
此時，H的鄰域里只有兩個點，H不是核心點，并且H此時也不能確定是不是邊界點，因此暫時將H標記為噪聲點。

接下來，以點I為半徑，2為圓心畫圓。I的鄰域中有三個點：H、I、J。因此I是核心點。由于J已經屬于類別1：{A，B，C，D，J}，因此I、H均加入類別1，不新建類：{A，B，C，D，J，H，I}。可見，H由噪聲點轉變為了邊界點。

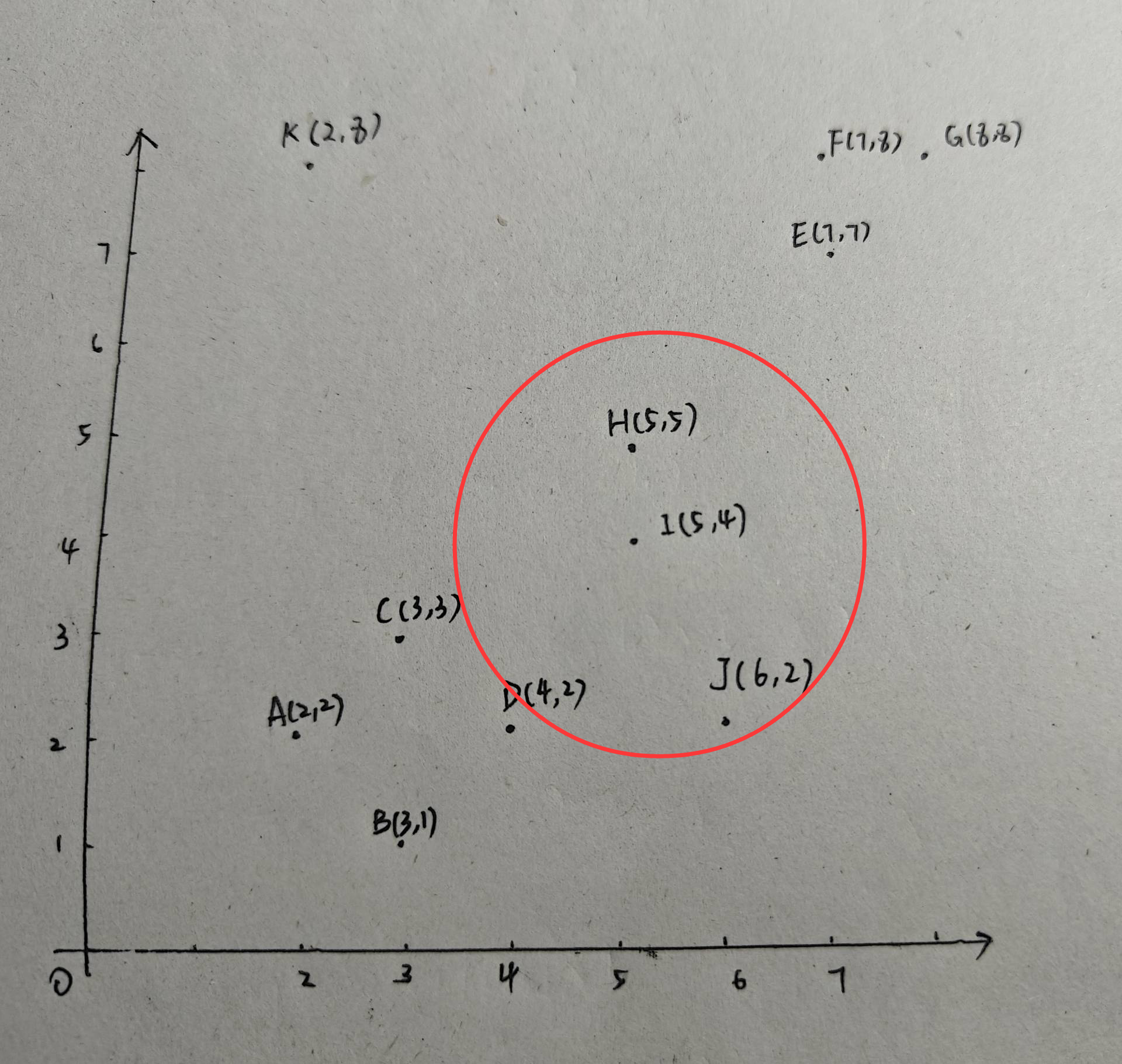
接下來，以J為圓心，2為半徑畫圓，J為核心點，但J已經在類別1中且沒有引入新點，故類別1保持不變。最后以K為圓心，2為半徑畫圓，K不是核心點也不是邊界點，因此K為噪聲點。

最終結果為：類別1，{A，B，C，D，J，H，I}；類別2，{E、F、G}；噪聲點：K

4、代碼實現

import numpy as np
from sklearn.cluster import DBSCAN
import matplotlib.pyplot as plt# 示例數據
X = np.array([[1, 1], [2, 1], [1, 3],  # 邊界點和噪聲點[8, 7], [8, 8], [9, 8], [10, 8],  # 簇C1[5, 5]  # 噪聲點
])# 應用DBSCAN
dbscan = DBSCAN(eps=1.5, min_samples=2)
labels = dbscan.fit_predict(X)# 可視化
plt.figure(figsize=(8, 6))
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis', s=100)
plt.title('DBSCAN聚類結果 (ε=1.5, MinPts=2)')
plt.grid(True)
plt.show()print("聚類標簽:", labels)  # 輸出: [ 0  0 -1  1  1  1  1 -1]
# -1表示噪聲點，0和1表示兩個不同的簇