給你一個滿足下述兩條屬性的?m x n?整數矩陣：

• 每行中的整數從左到右按非嚴格遞增順序排列。
• 每行的第一個整數大于前一行的最后一個整數。

給你一個整數?target?，如果?target?在矩陣中，返回?true?；否則，返回?false?。

示例 1：

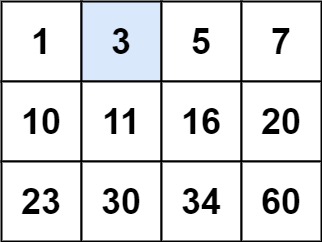
輸入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
輸出：true

示例 2：

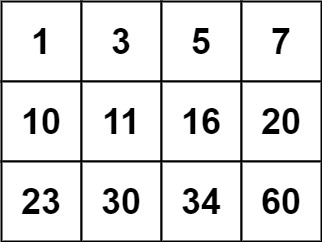
輸入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
輸出：false

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 100
• -104 <= matrix[i][j], target <= 104

若將矩陣每一行拼接在上一行的末尾，則會得到一個升序數組，我們可以在該數組上二分找到目標元素。

代碼實現時，可以二分升序數組的下標，將其映射到原矩陣的行和列上。

class Solution {
public:bool searchMatrix(vector<vector<int>>& matrix, int target) {int m = matrix.size(),n = matrix[0].size();int low = 0,high = m * n - 1;while(low <= high){int mid = (high - low) / 2 + low;int x = matrix[mid / n][mid % n];if(x < target){low = mid + 1;}else if(x > target){high = mid - 1;}else{return true;}}return false;}
};