一、計數排序（Counting Sort）

計數排序是一種非比較型的排序算法，它的核心思想是：

利用“元素的值”來確定它在結果數組中的位置，通過“統計每個數出現的次數”來完成排序。

二、如何實現計數排序（核心步驟）

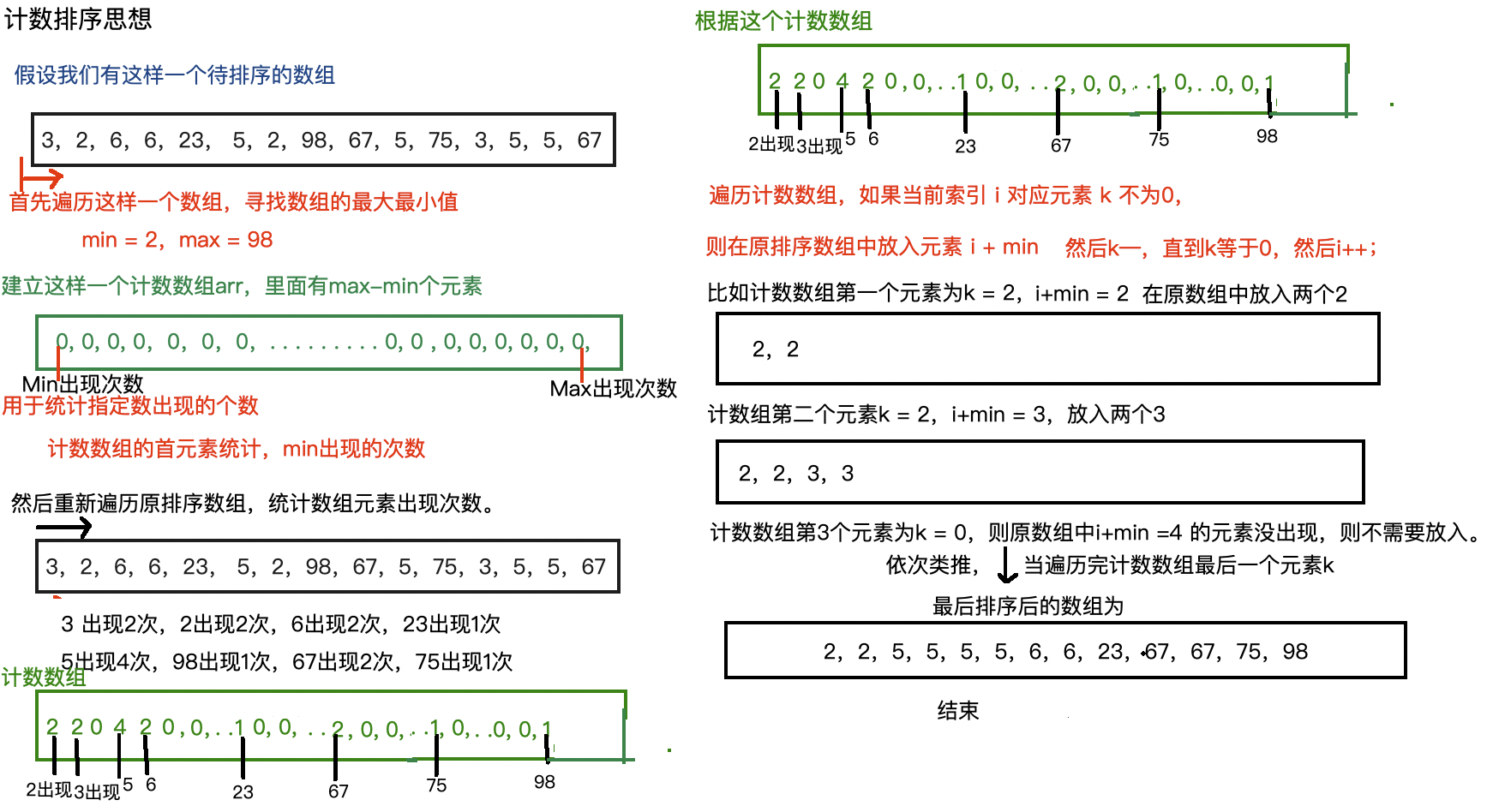
1、設有一個待排序數組?arr，長度為?n，值的范圍是?[min, max]。

2、找最大最小值，確定計數數組大小

3.?創建計數數組并統計頻次

4.?恢復到原數組（非穩定排序）

思維導圖

代碼實現

void Count_Sort(int* arr,int size){assert(arr);int min = arr[0];int max = arr[0];for(int i = 1;i<size;i++){if(arr[i]<min){min = arr[i];}if(arr[i]>max){max = arr[i];}}int Range = max-min+1;int index = 0;int* Count_Arr = (int*)calloc(Range,sizeof(int));for(int i = 0;i<size;i++){Count_Arr[arr[i]-min]++;};for(int j = 0;j<Range;j++){while (Count_Arr[j]--){arr[index++] = min+j;}}return;
}

三、計數排序優缺點

四、應用場景：

• 排序范圍已知、較小的數據（例如考試成績、年齡、投票數等）

• 多關鍵字排序中的一環（如基數排序的子排序）

五、所學習過的排序算法總結

穩定性的介紹：數組中相同值，排完序的相對順序是否可以做到不變，如果不變就是穩定的，如果會變化就是不穩定的。