算法	相關知識點	可以通過點擊	以下鏈接進行學習	一起加油！

動態規劃是一種解決最優化問題的強大技術，通過將問題分解為子問題并逐步求解來實現高效計算。斐波那契數列是動態規劃中經典的應用之一，其遞推關系非常適合用動態規劃進行優化。通過動態規劃，我們不僅能避免重復計算，從而大幅提高計算效率，還能直觀地理解遞推模型在實際問題中的應用。本文將帶你深入理解斐波那契數列的遞推模型，展示如何利用動態規劃來優化其計算過程，并探討這一方法的實際價值與應用。

🌈個人主頁：是店小二呀
🌈C/C++專欄：C語言\ C++
🌈初/高階數據結構專欄： 初階數據結構\ 高階數據結構
🌈Linux專欄： Linux
🌈算法專欄：算法
🌈Mysql專欄:Mysql

🌈你可知:無人扶我青云志 我自踏雪至山巔

動態規劃前言介紹

動態規劃（Dynamic Programming, DP）是一種解決最優化問題的方法，它將復雜問題拆解成多個簡單的子問題，通過保存子問題的解來避免重復計算，從而提高計算效率。

動態規劃適用于具有重疊子問題和最優子結構的場景：

1. 重疊子問題：問題可以被分解成相同的子問題，且子問題會重復計算。通過存儲這些子問題的解，可以避免重復計算，節省時間。
2. 最優子結構：問題的最優解可以通過其子問題的最優解來構建，即最優解是由子問題的最優解組合而成。

【動態規劃的基本思路】：

1. 狀態表示

• 這一部分是指DP表里面的值所表達的含義。通常可以從以下三個角度來確定：
  1. 題目要求：從題目的要求來定義狀態。
  2. 經驗 + 題目要求：結合經驗和題目要求確定狀態。
  3. 分析問題的過程中，發現重復子問題：在分析問題時，可以發現哪些是重復的子問題，進而決定狀態的定義。

2. 狀態轉移方程

• 狀態轉移方程描述了當前狀態如何由前一個或多個狀態推導出來。例如，dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3]，這表示當前狀態是由前幾個狀態的值組合而成的。

3. 初始化

• 設置初始狀態，以確保在填表時不會越界。比如，對于斐波那契數列，dp[0]和dp[1]可能需要提前設定為已知的初始值。

4. 順序計算

• 在填充狀態表時，必須保證填充當前狀態時，所依賴的先前狀態已經計算出來。這通常意味著需要按照一定的順序（例如，從小到大）來計算狀態。

5. 返回值

• 根據題目要求，返回最終的狀態值。例如，如果我們計算的是最短路徑、最大值或最優解，返回的是狀態表中相應位置的值。

---

1137第 N 個泰波那契數

【題目】：1137. 第 N 個泰波那契數

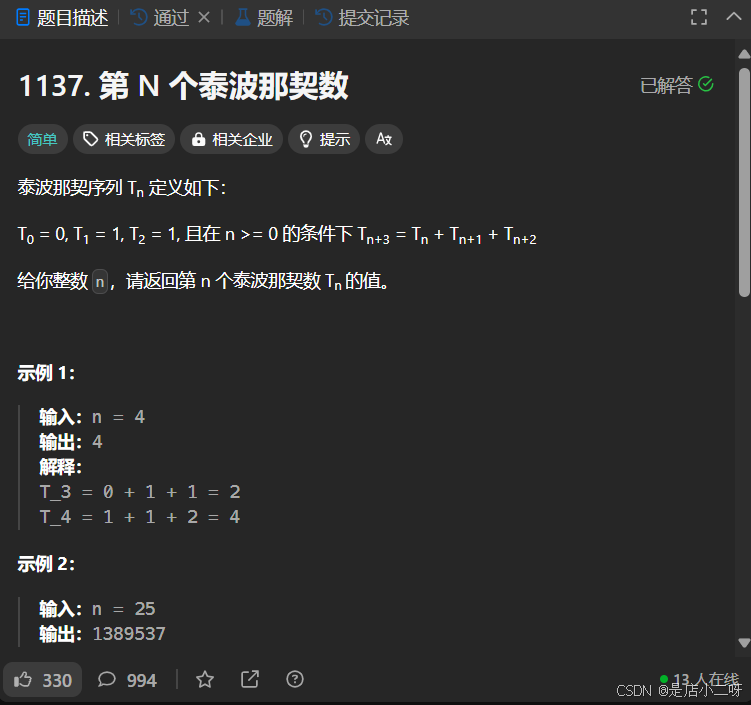
【算法思路】

這道題典型地使用動態規劃（DP）來快速計算所需元素，流程如下：

1. 創建 DP 表
2. 初始化
3. 填表
4. 返回結果

【代碼實現】

class Solution {
public:int tribonacci(int n) {if(n == 0) return 0;if(n == 1 || n == 2) return 1;vector<int> dp(n + 1);dp[0] = 0;dp[1] = dp[2] = 1;for(int i = 3; i <= n; i++)dp[i] = dp[i - 1] + dp[i - 2] + dp[ i- 3];return dp[n];}
};

【優化方案】：滾動數組

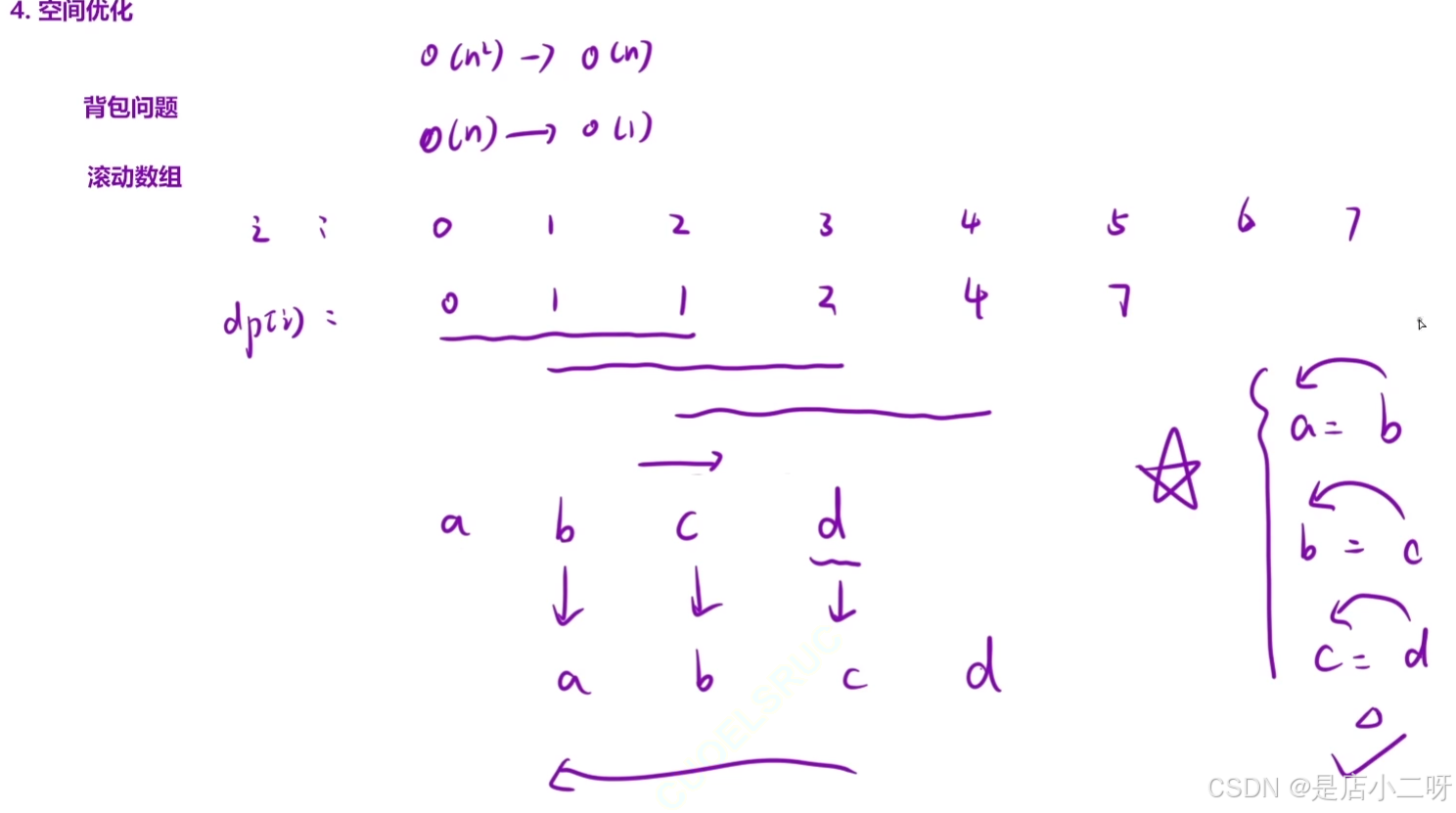
class Solution {
public:int tribonacci(int n) {if(n == 0) return 0;if(n == 1 || n == 2) return 1;vector<int> dp(n + 1);int a = 0, b = 1, c = 1, d = 0;for(int i = 3; i <= n; i++){d = a + b + c;//滾動操作 a = b; b = c; c =d;}return d;}
};

---

面試題 08.01. 三步問題

【題目】：面試題 08.01. 三步問題

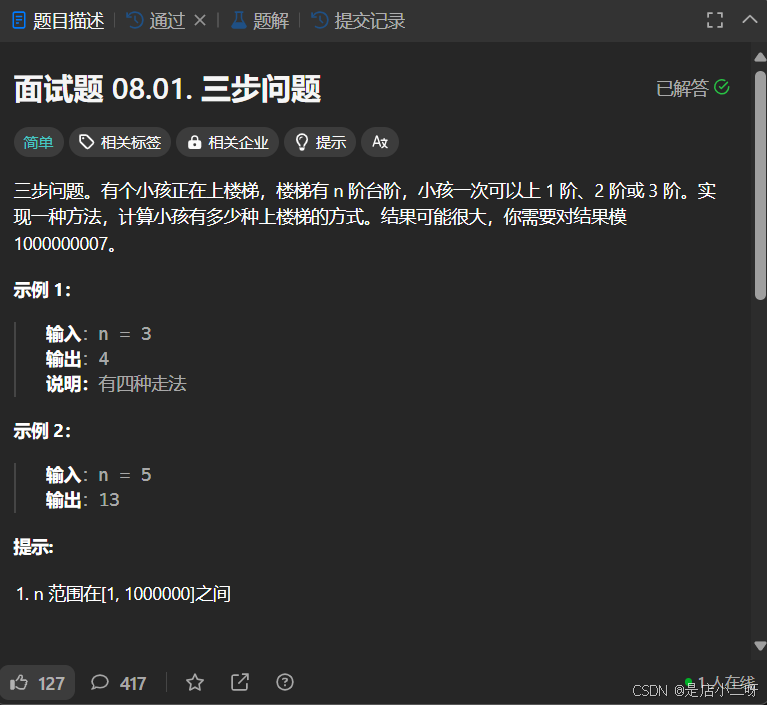
【算法思路】

面對未知的題目時，可以通過繪圖尋找線索，幫助解決問題。例如，在這道題中，確定一個位置并列舉所有可能情況，可以發現規律。比如，表示i位置前面三次的情況，所有可能組合加起來就是i位置的答案。

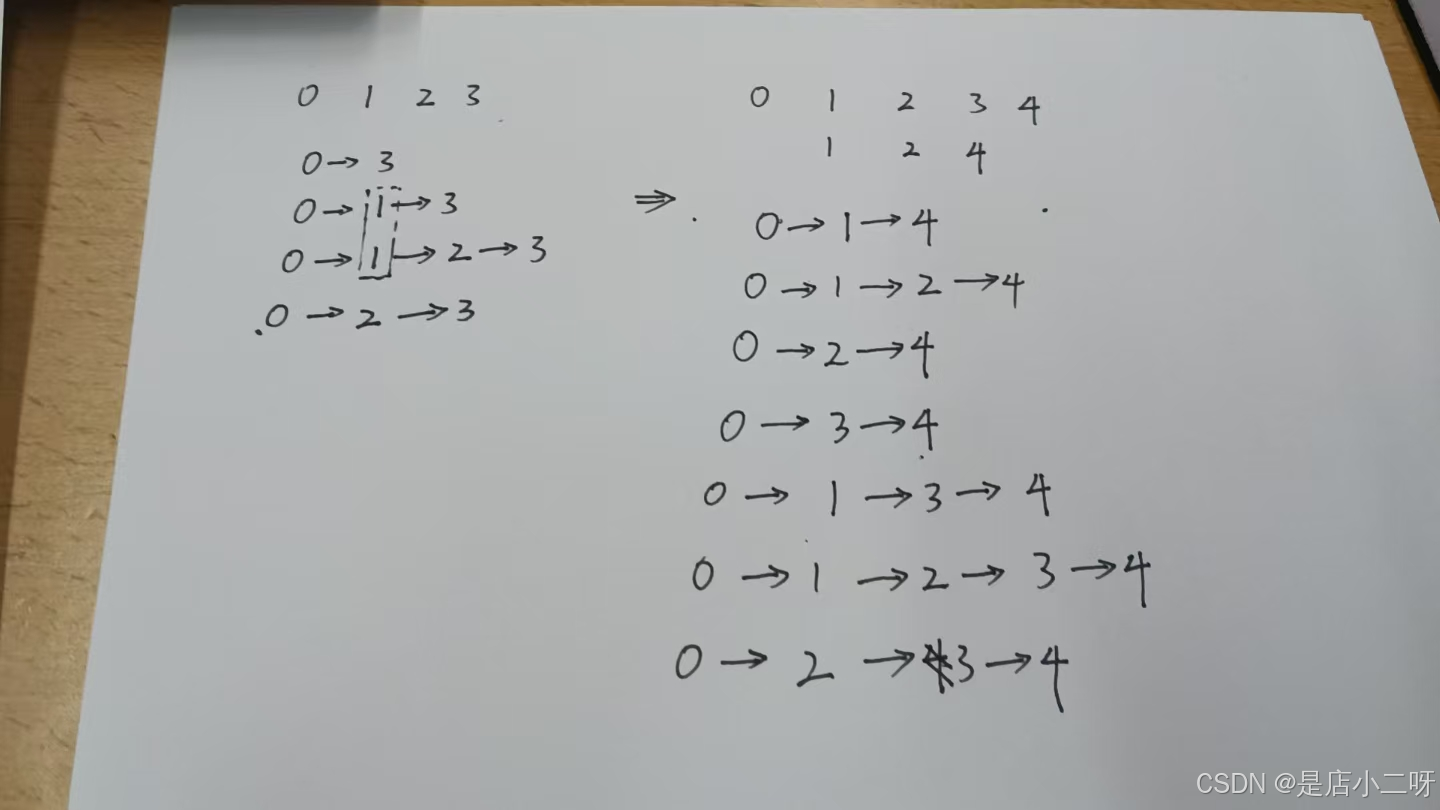
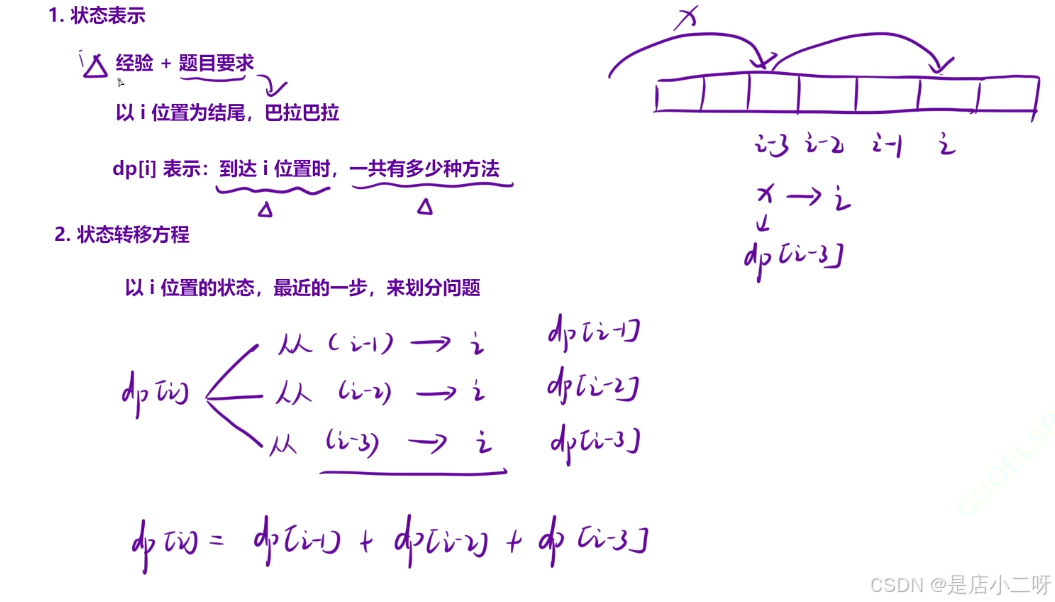
筆試中不需要使用滾動數組，也不用花時間去做空間優化。平時不必刻意練習這些，效果有限。

【代碼實現】

class Solution {
public:int waysToStep(int n) {//1.創建dp表vector<int> dp(n + 2);if(n == 1 || n == 2) return n;if(n == 3) return 4;const int MOD = 1e9 + 7;//2.初始化dp[1] = 1;dp[2] = 2; dp[3] = 4;//3.填表for(int i = 4; i <= n; i++)dp[i] = ((dp[i - 1] + dp[i - 2])%MOD + dp[i - 3])%MOD;return dp[n];}
};

【細節問題】

對于這類需要取模的問題，每次計算（如加法、乘法等）都要取一次模，以防止溢出，否則答案可能會錯誤

---

LCR 088. 使用最小花費爬樓梯

【題目】：LCR 088. 使用最小花費爬樓梯

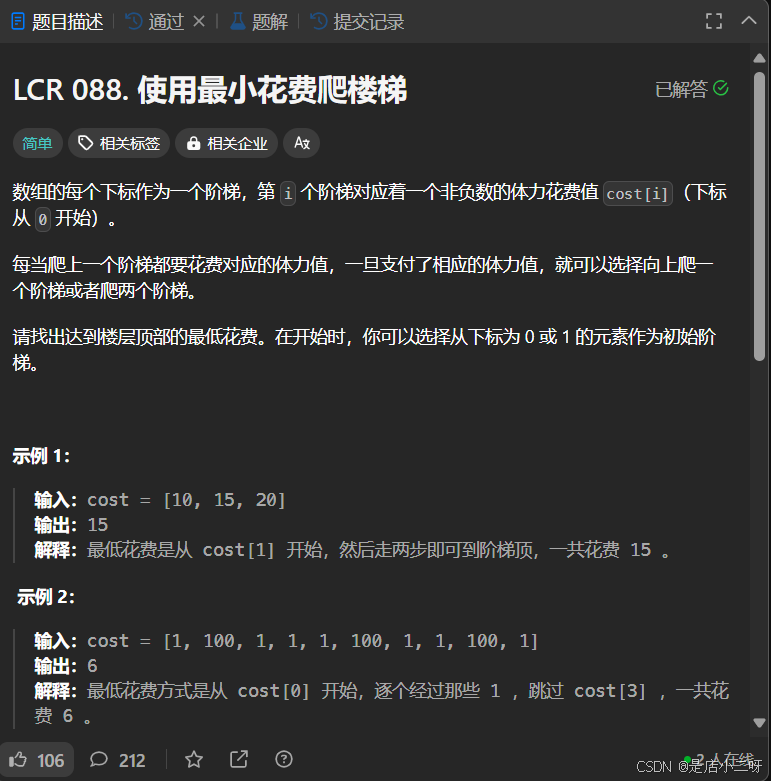
【算法思路】

解法一：

【小技巧】：通過之前或之后的狀態推導出 dp[i] 的值。這類問題通常需要通過隱含或明確的遞推關系來確定某個位置的數值。

【代碼實現】

class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {int n = cost.size();//1.創建dp表vector<int>dp (n + 1);//2.初始化dp[0] = dp[1] = 0;//3.填表for(int i = 2; i <= n; i++)dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);return dp[n];}
};

【算法思路】

解法二：

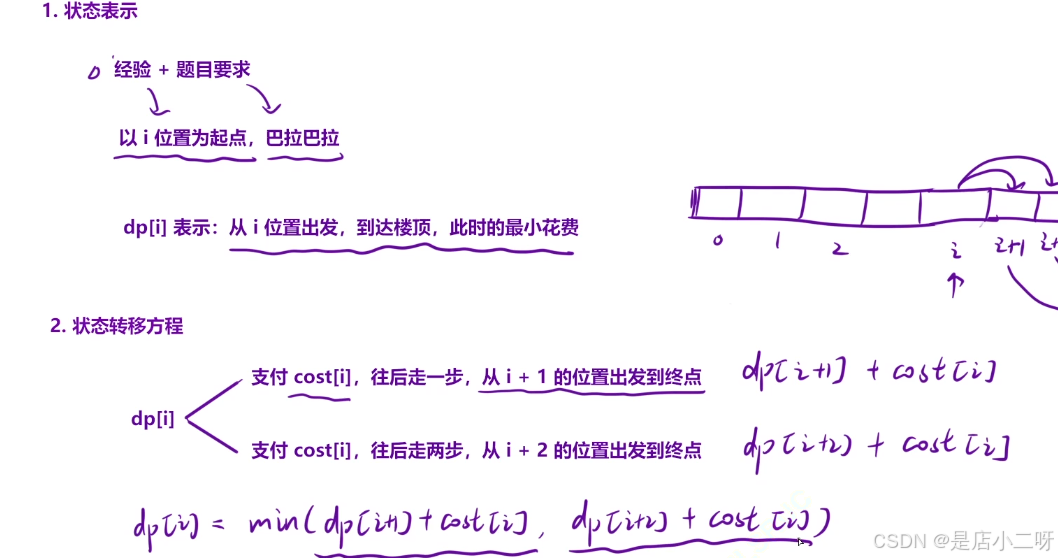
【代碼實現】

class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {int n = cost.size();//1.創建dp表vector<int>dp (n);//2.初始化dp[n - 1] = cost[n -1]; dp[n - 2] = cost[n - 2];//3.填表for(int i = n - 3; i >= 0; i--)dp[i] = min(dp[i + 1], dp[i + 2]) + cost[i];return min(dp[0], dp[1]);}
};

---

91. 解碼方法

【題目】：91. 解碼方法

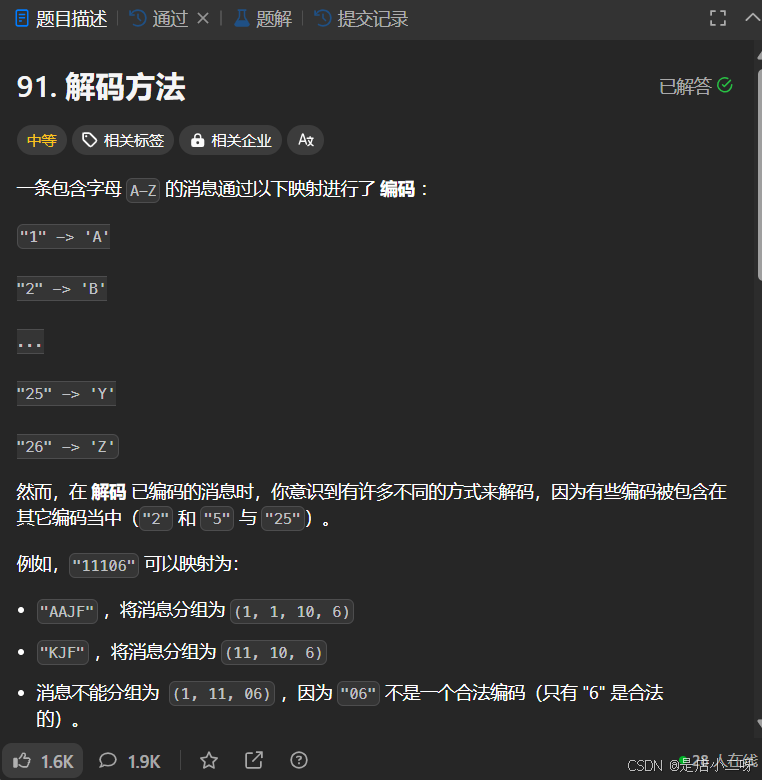
【算法思路】

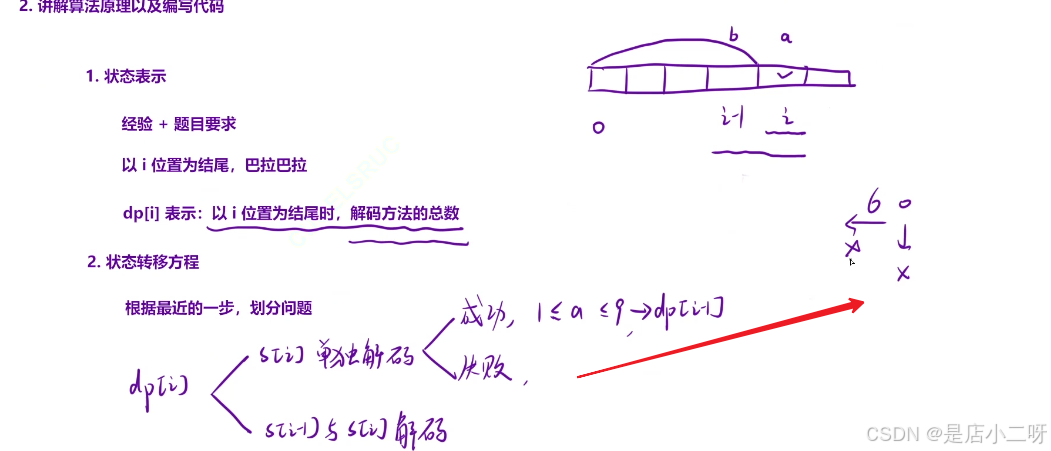
我們使用 dp[i] 表示以位置 i 結尾時的解碼方法總數。在分析位置 i 時，需要考慮兩種情況：一種是單獨解碼 s[i]，另一種是將 s[i-1] 和 s[i] 結合解碼。對于后者，必須滿足 s[i-1]s[i] 形成一個有效的兩位數（即在1到26之間，且沒有前導零）。

因此，狀態轉移方程為：dp[i] = dp[i-1] + dp[i-2]，但只有在滿足解碼條件時，才能進行累加。這樣，我們能夠從整體上分析解碼的方案，而不是孤立地考慮每個子問題的解。

【個人思考】

通過整體思路來解決解碼方案問題，結合這兩張圖片，可以更直觀地理解解法。

為什么是相加，難道不會重復嗎？其實，每個位置的解碼方式是基于前面所有元素的解碼結果，解法數量是通過添加‘單獨解碼’和‘雙位解碼’的方式得到的。因此，需要將之前的解碼方案數相加，因為每個步驟都是缺一不可的。

【代碼實現】

class Solution {
public:int numDecodings(string s) {              int n = s.size();//1.創建dp表vector<int> dp(n);//2.初始化dp[0] = s[0] != '0';if(n == 1) return dp[0];if(s[1] >= '1' && s[1] <= '9') dp[1] += dp[0];int t = (s[0] - '0') * 10 + (s[1] - '0');if(t >= 10 && t <= 26) dp[1] += 1;//3.填表操作for(int i = 2; i < n; i++){if(s[i] >= '1' && s[i] <= '9') dp[i] += dp[i - 1];int t = (s[i - 1] - '0') * 10 + (s[i] - '0');if(t >= 10 && t <= 26) dp[i] += dp[i - 2];}return dp[n - 1];}
};

快和小二一起踏上精彩的算法之旅！關注我，我們將一起破解算法奧秘，探索更多實用且有趣的知識，開啟屬于你的編程冒險！