喜歡的話別忘了點贊、收藏加關注哦（關注即可查看全文），對接下來的教程有興趣的可以關注專欄。謝謝喵！(=^･ω･=)

4.3.1. 實戰中會遇到的問題

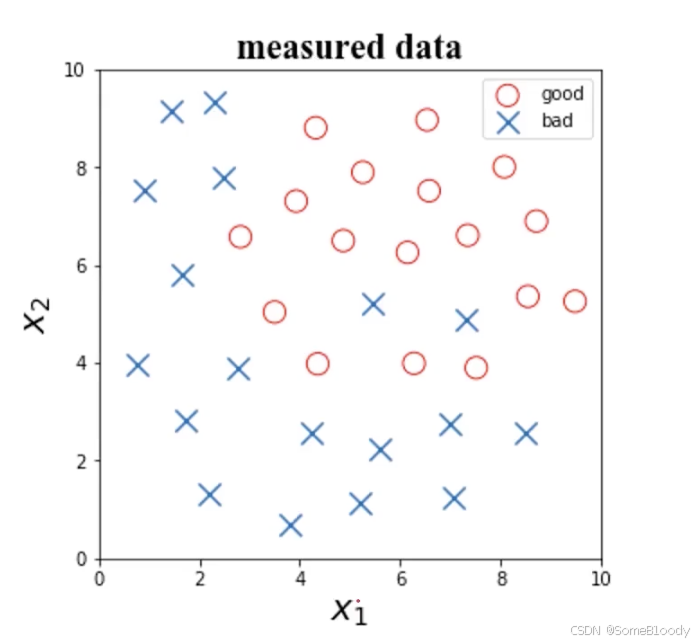
首先看一個例子：

根據任檢測數據$x_1$、$x_2$及其標簽，判斷$x_1=6$，$x_2=4$時所屬的類別。

圖像如下：

我們接下來就需要選擇算法了，可選擇的有：

• 邏輯回歸(詳見 1.6. 邏輯回歸理論)
• KNN(詳見 2.2. 聚類分析算法理論)
• 決策樹(詳見 3.1. 決策樹理論)
• 神經網絡(之后會講)

選擇完算法之后我們還會遇到一個問題：具體算法的核心結構/參數如何選擇？

• 如果選擇邏輯回歸：邊界函數用什么？用線性函數還是多項式？
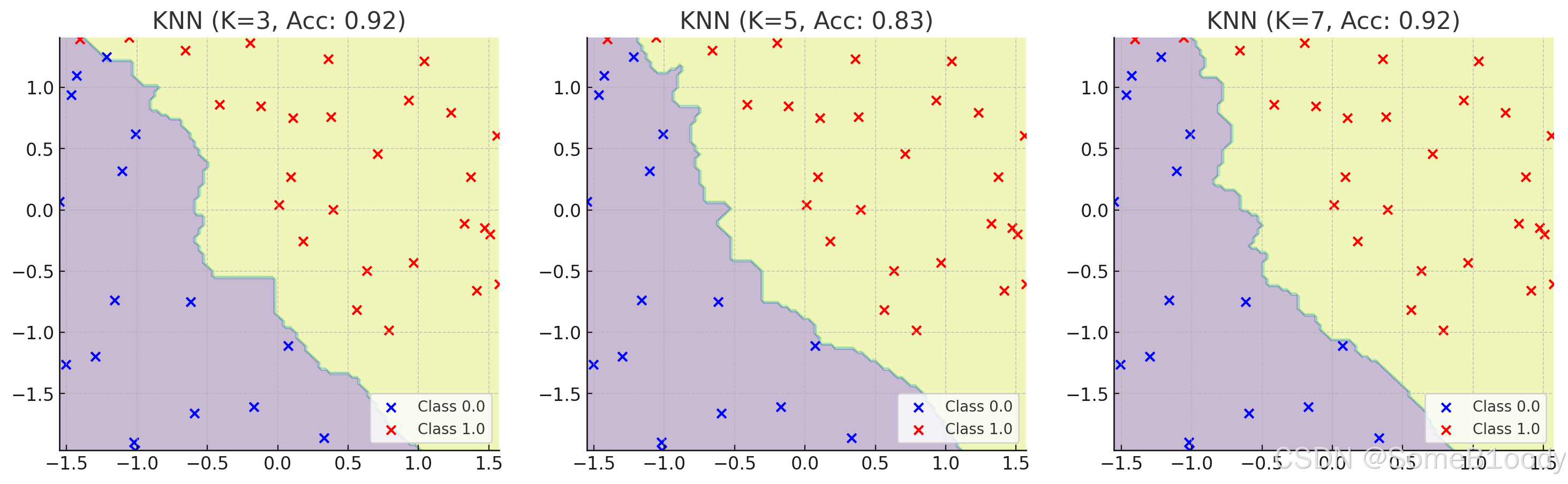
• 如果選擇KNN：核心參數n_neighbors（指定的K值）取多少合適？
• …

最后，如果模型表現不佳，具體表現為

• 訓練數據準確率太低(欠擬合)
• 測試數據準確率下降明顯(過擬合)
• 召回度/特異度/精確率低

這種情況下我該怎么辦呢？

這些情況匯總下來就是一個問題：如何提高模型表現？

4.3.2. 數據決定上限

數據的質量決定了模型表現的上限。就算你用再強的模型/參數，只要你的數據質量差效果就好不起來。

建議在建模之前先檢查數據的以下方面：

• 數據屬性的意義，是否為無關數據
• 不同屬性數據的數量級差異性如何
• 是否有異常數據
• 采集數據的方法是否合理，采集的數據是否有代表性
• 對于標簽結果，要確保標簽判定規則的一致性(統一標準)

對數據進行的操作	好處
刪除不必要的屬性	防止過擬合，節約運算時間
數據預處理：歸一化、標準化	平衡數據影響，加快訓練收斂
確定是否保留或過濾掉異常數據	提高實用性
嘗試不同的模型，對比模型表現	幫助確定更合適的模型

以上文的例子來說，在我們獲得數據之后，我們要考慮以下問題：

• 是否有需要剔除的異常數據？
• 數據量級差異如何？
• 是否需要降低數據維度？

對于檢查異常數據這一部分，我們學過異常檢測(詳見 3.3. 異常檢測(Anomaly Detection)理論)，通過概率密度函數來找潛在的數據異常點。

對于數據量級差異的部分，我們要先看數據的分布，$x_1$的數據分布在0.77～9.49，$x_2$的數據分布在0.69~9.5。這兩個變量的數據分布基本相同，可以不做歸一化處理。

對于確認是否需要降低數據維度的部分，我們需要先對數據進行主成分分析(詳見 3.4. 主成分分析(PCA)理論)。由于例子中的數據只有2個維度，所以就不需要進行主成分分析來降維了，具體的操作見 3.7. 主成分分析(PCA)實戰。

4.3.3. 嘗試不同的模型

不同的模型通常會有不同的效果，你可以計算準確率并可視化出來，這里的數據使用的是 1.9. 邏輯回歸實戰 中的，我把.csv數據文件放在GitCode上了，點擊鏈接即可下載。

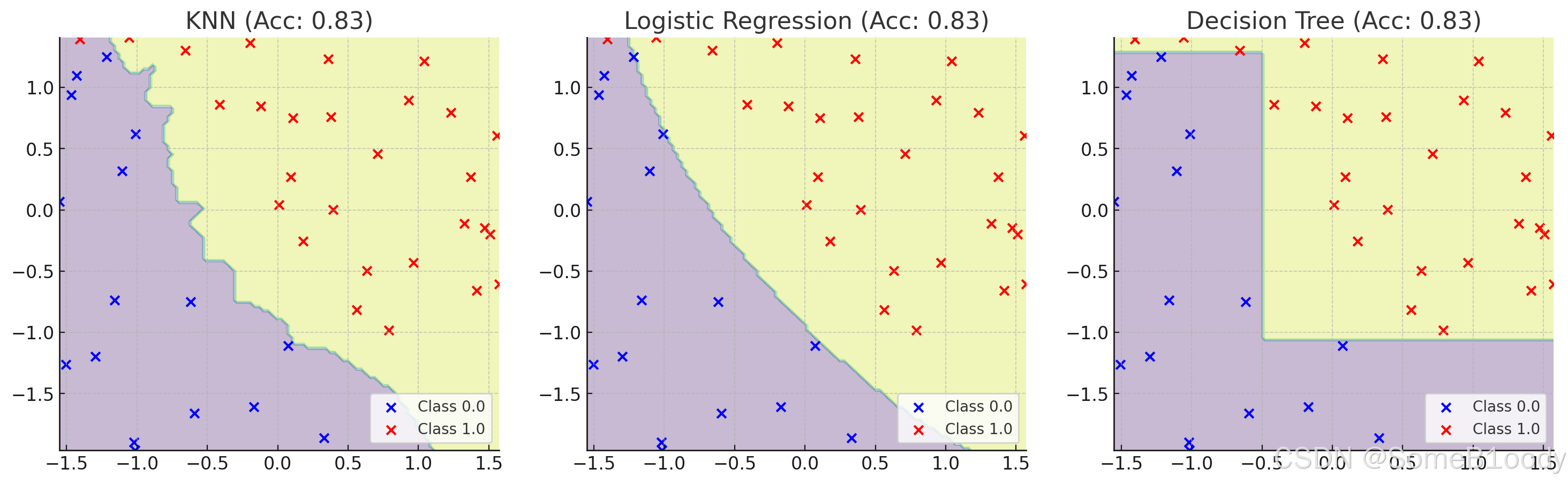
你也可以通過混淆矩陣來計算其它參數，根據其他指數來決定要使用哪個模型。衡量指標的選擇取決于應用場景：

• 垃圾郵件檢測（正樣本為“垃圾郵件“）：希望普通郵件（負樣本）不要被判斷為垃圾郵件（正樣本），即：判斷為垃圾郵件的樣本都是判斷正確的，需要關注精確率；還希望所有的垃圾郵件盡可能被判斷出來，需要關注召回率。
• 異常交易檢測（正樣本為“異常交易”）：希望判斷為正常的交易（負樣本）中盡可能不存在異常交易，還需要關注特異度。

4.3.4. 其他調整

在確定了該使用什么模型之后，我們還需要對其他方面進行微調：

• 遍歷核心參數組合，評估對應模型表現（比如：邏輯回歸邊界函數考慮多項式、KNN嘗試不同的n_neighbors值）
• 擴大數據樣本
• 增加或減少數據屬性
• 對數據進行降維處理(主成分分析PCA)
• 對模型進行正則化處理，調整正則項$\lambda$的數值(詳見 4.1. 過擬合(overfitting)與欠擬合(underfitting) )

來看看KNN的n_neighbors值對結果的影響：