目錄
1. 未標記樣本
2. 生成式方法? 高斯混合+EM
3. 半監督SVM? 存在未標記樣本的SVM變形
4. 圖半監督學習 對圖權值迭代矩陣計算
5. 基于分歧的方法 多視圖協同訓練
6. 半監督聚類 k-means的條件變形
6.1 Constrained k-means 利用“必連”與 “勿連”約束
6.2?Constrained Seed k-means 少量有標記的樣本
在監督與無監督之間，少量標記樣本的情況下，如何相比純監督學習充分利用無標記樣本的分布特征，相比無監督學習利用少量的已知信息？
對高斯混合分布、SVM、k-means進行一些修正和改進。
建模圖論節點、邊權迭代的思想；多視圖協同訓練、互相學習的思想。
1. 未標記樣本
標記樣本太少 用來訓練不夠； 還有很多未標記樣本 全標記需要的成本太高
主動學習 active learning：每次挑對改善模型性能幫助大的樣本 用少的專家查詢 換取高性能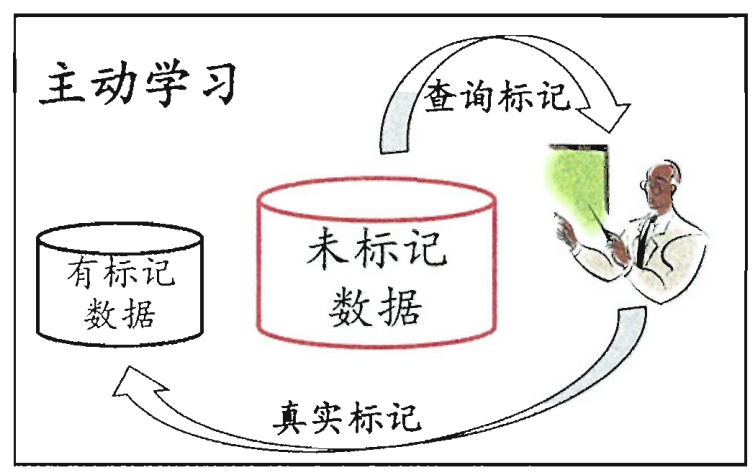
若不引用額外的專家知識可以嗎？因為標記或未標記樣本 都是由相同數據源 獨立同分布采樣
我們可以利用觀察到的總樣本分布：
聚類假設：假設數據存在簇結構，同一個簇的樣本屬于同一個類別
流形假設：假設數據 分布在一個流形結構上，鄰近的樣本擁有相似的輸出值
比如這里 帶判別樣本是在標記正負中間 無法判斷；
但把他們放在樣本群里面 發現左邊那一大塊更有可能是+ 這個帶判別也更有可能是正
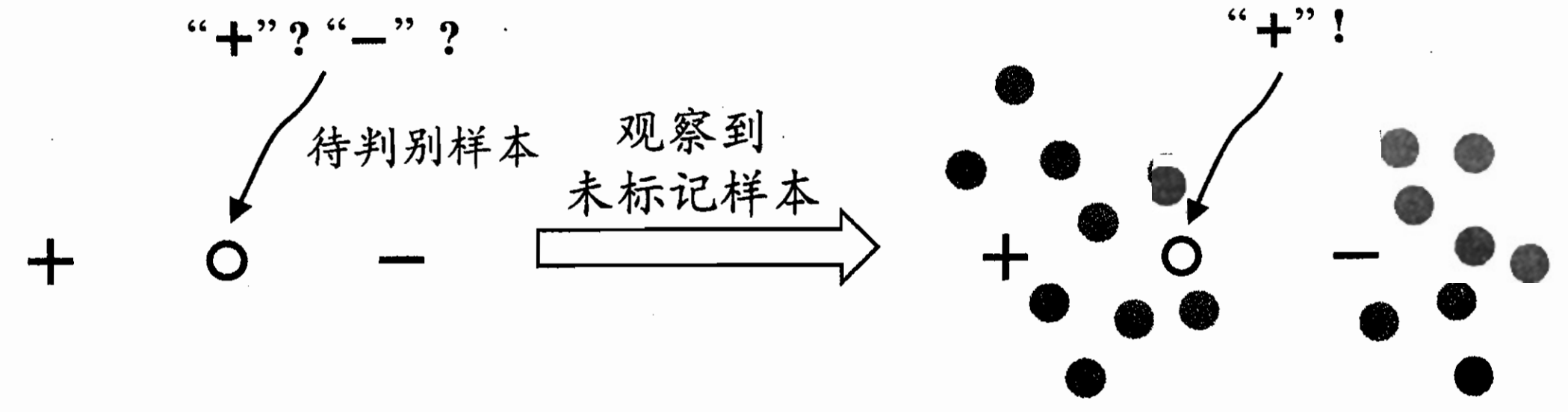
半監督學習：讓學習器不依賴外界交互、 自動地利用未標記樣本來提升學習性能
純半監督學習：目標是預測樣本外未觀測到的數據
直推學習：目標是預測樣本中?未標記數據
2. 生成式方法? 高斯混合+EM
前置思想 周志華《機器學習導論》第9章 聚類中的高斯混合分布
樣本由N個高斯分布加權組合而成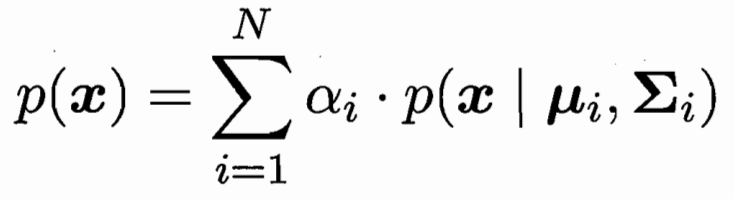
樣本x屬于第i個高斯分布的概率為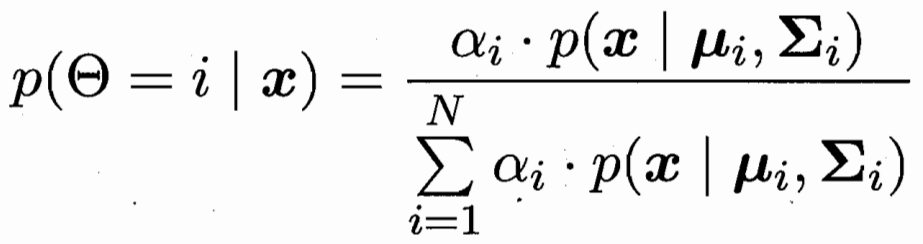
樣本x對應后驗概率最大的類別 j? ? ?條件概率 第i個高斯下的類別 j
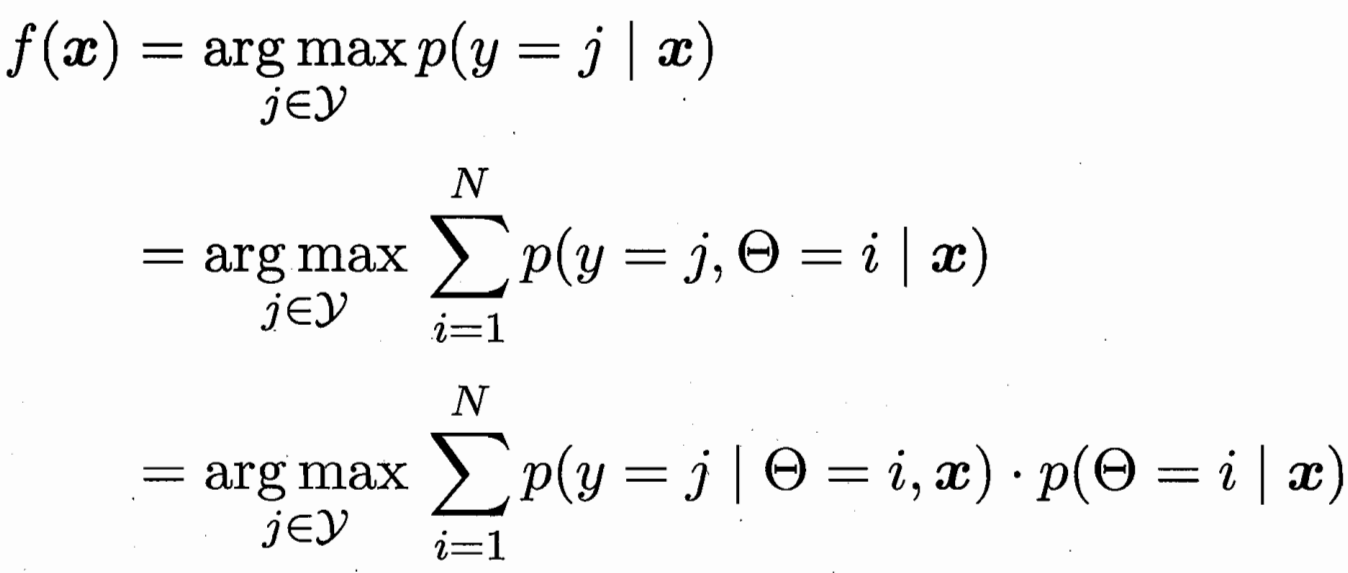
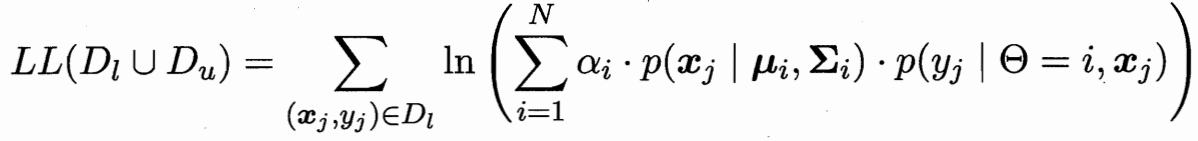
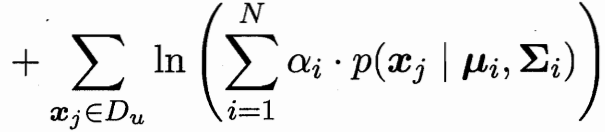?極大似然估計 有標記的為(x,y)概率 無標記的為x概率
隱變量估計 EM算法?模型推隱變量-隱變量更新模型 重復至收斂
隱變量為 未標記樣本 屬于類別i高斯分布的概率
模型參數有：把未標記樣本 依概率加權算作類i 更新類i的均值 方差 權重
3. 半監督SVM? 存在未標記樣本的SVM變形
TSVM 二分類：所有m個未標記樣本（每個樣本可能+ - 共2^m個可能里）
對于每一種可能 都SVM一下 選所有可能里間隔最大的那個劃分超平面
周志華《機器學習導論》第5章 支持向量機SVM 前情回顧
這里的區別：之前有標記的 判別錯誤的懲罰項系數 比無標記的懲罰要高（前l有標記 后m無標記）
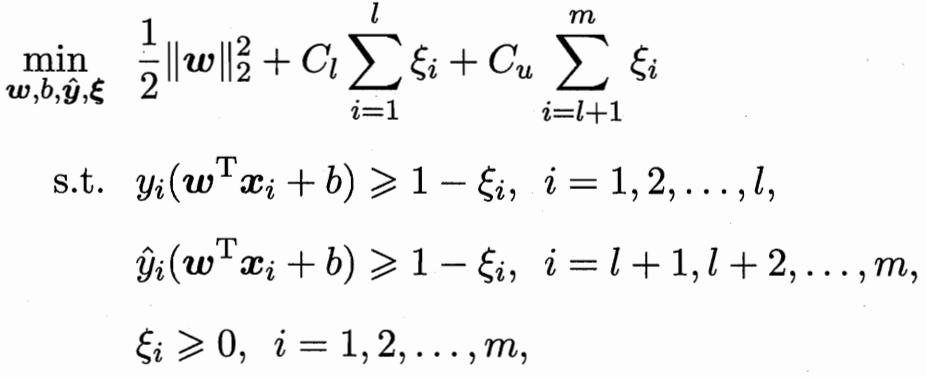
但這樣2^m個超平面 計算復雜度還是太高了 考慮局部搜索迭代近似
先根據標記樣本算出超平面 未標記樣本根據超平面打上初始標記 Cu權重遠小于Cl
1.把兩個一正一負的 且出錯可能性相對比較高（相加＞2）的標簽 進行正負對調?
2.把所有兩兩都檢查一下后，重算SVM 并調高Cu權重。
一直重復1 2調整 直到Cu權重接近Cl。
?
為防止+ - 類別不平衡，進行調整權重操作 按照正負項數反比例
?
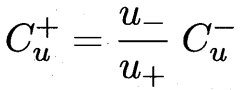
4. 圖半監督學習 對圖權值迭代矩陣計算
建模成圖 每個樣本為點 邊值為兩樣本的相似度大小（可用高斯函數）
已標記樣本為染色點 圖半監督問題相當于擴展染色/傳播 問題?
?
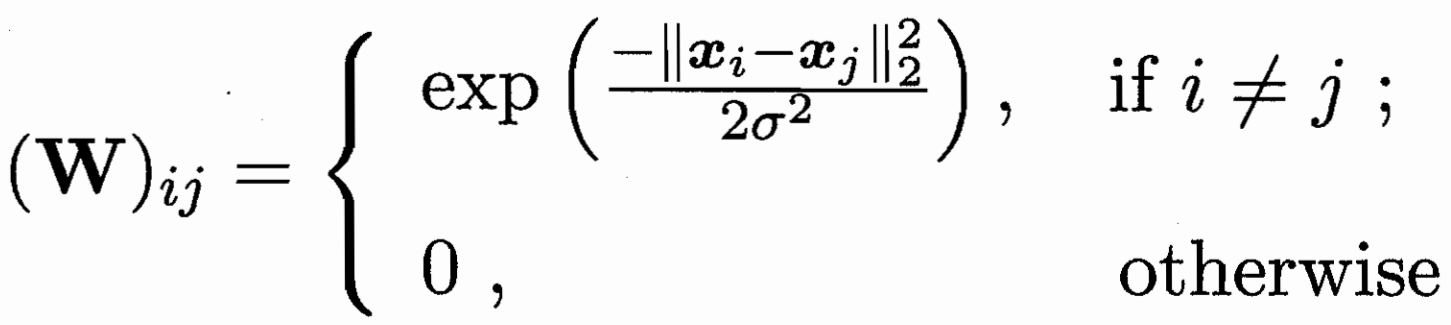要學習一個函數f 可以把樣本向量x 映射到一個值? 把f前l和后u拆解??fl已知?需要優化 fu
目標函數為 最小化能量函數 W大的需要讓他們的f接近
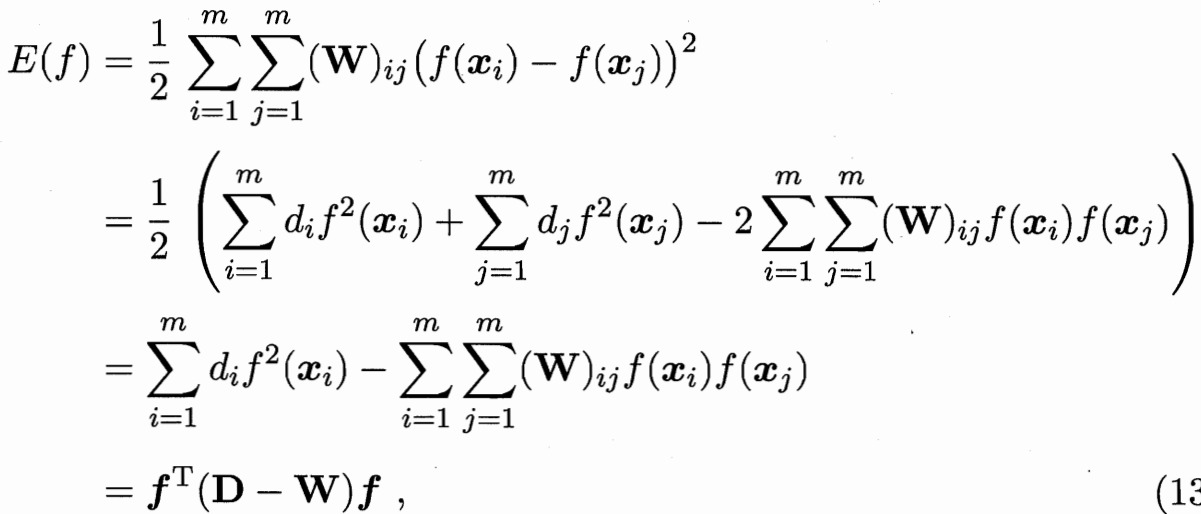
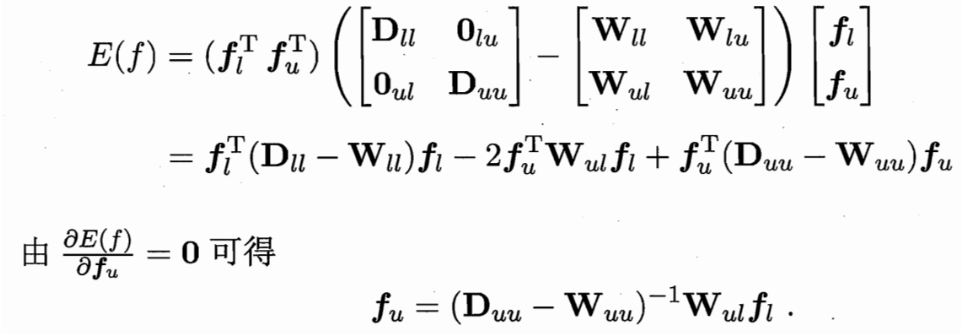
用一個 P=D逆W 可用Puu Pul 簡化式子
?
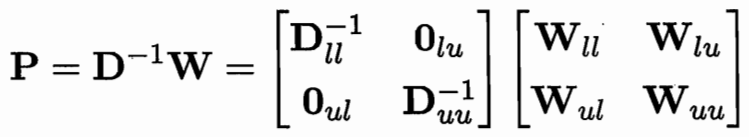
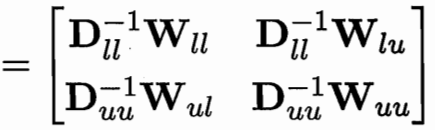
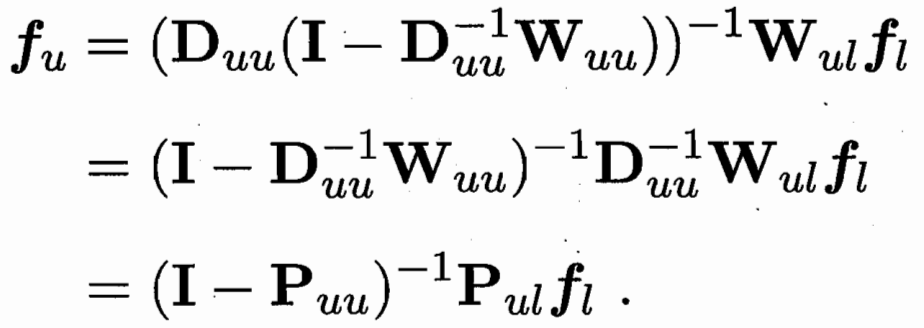W可以推 D和P 求偏導得 fu和 fl的關系
如果是多分類的標記傳播：f就不是映射到值 而是F 映射到一個向量；
每個樣本 都會映射到一個長度為 |y| 的向量
最后的值為 向量最大數的位置（評估一下和每個類的相似度 分為相似度最大的那個）
初始的F是 前l樣本對應的那類位置為1 矩陣其余位置均為0? ? ? 一直迭代到F*收斂
S為W除以度數 歸一化（防止高度數節點過度影響結果 保證特征值在[-1,1]內 使迭代過程收斂）
α的系數為迭代? (1-α)為保持初始Y的特征
? 令F(t+1)=F(t)
5. 基于分歧的方法 多視圖協同訓練
多視圖數據：同一個數據對象不同方面的屬性（如視覺、聽覺上的）
協同訓練：利用多視圖的 相容性（判別答案的類別空間y相同）和互補性
假設數據擁有兩個充分(每個視圖都包含足以產生最優學習器的信息)且
條件獨立（在給定類別標記條件下兩個視圖獨立）視圖：?
每個視圖的學習器，把自己最有把握的未標記樣本打上標簽給其他學習器學習（互相學習）
我知道你的信息 -> 我學到新東西告訴你 -> 你根據我的新信息 學到新東西告訴我
為防止所有樣本都被大量改變：構建一個緩沖池 每次從緩沖池里找最有把握的
每次循環 對每個視圖分別：1.根據已有數據訓練分類器
2.在緩沖池里找 p個最有把握的正類和 n個最有把握的負類 打標記后 移除緩沖池
3.每個視圖進行完畢后 補充緩沖池 從樣本池隨機抽一定樣本移到緩沖池? ?維持每次循環前緩沖池中樣本數目一定
6. 半監督聚類 k-means的條件變形
聚類本來無監督 但是有一些額外的信息的話 可以幫助聚類效果更好（帶限制的k-means）
6.1 Constrained k-means 利用“必連”與 “勿連”約束
還是k個均值點μ 代表k個簇
每個樣本依次塞到最近的 不違背“必連勿連約束”的簇；? ?分類好再取新的均值μ； 上兩步迭代
6.2?Constrained Seed k-means 少量有標記的樣本
用帶標記的樣本 初始化的k個μ；
并在后續的迭代過程中 不改變這些樣本；無標記的樣本類似傳統k-means
)
)
