自線性回歸以來，我們已經涵蓋了很多領域。在本期中，我們將開始了解神經網絡內部工作原理的旅程*。*

如果一個人試圖了解任何使用生成式 AI 的工具、應用程序、網站或其他系統的內部工作原理，那么掌握神經網絡的架構至關重要。在這個故事中，我們將討論神經網絡的所有主要組件，以及如何在 Python 中構建神經網絡對象。

什么是神經網絡？

神經網絡是一種機器學習算法，它以類似于人腦運作方式的方式對數據進行建模。神經網絡由一系列相互連接的節點組成，很像大腦中的神經元。信息流經每個節點，縱，并產生輸出。此過程會發生多次，在每次傳遞期間，網絡會根據結果對某些目標變量的偏離目標程度來調整信息的處理方式。神經網絡有幾種類型，在本文中，我們將重點介紹多層感知器 （MLP）。但是，我們將討論的所有概念都將與所有類型的神經網絡相關。

層 & 節點

典型的神經網絡將由一個輸入層、一個輸出層和一個或多個隱藏層*（輸入層和輸出層之間的層）組成。這就是 Deep Learning 一詞的由來。每一層都將由一系列節點組成。在輸入層中，節點表示特征變量的向量。在每一層之間，數據使用特定函數（通常是線性函數）進行轉換，其中權重和偏差項是隨機生成的。然后，此函數的輸出通過另一個稱為激活函數的函數。將 input 層之后的后續層視為原始數據的復雜轉換。最后一層稱為輸出層，我們在其中預測模型的目標變量。我們預測的變量類型將決定我們在最后一層和輸出層之間使用的激活函數類型。數據通過網絡后，我們可以通過計算損失函數來了解它對目標變量的預測效果如何。通過一個稱為反向傳播的過程，**損失函數的結果用于調整權重和偏置項，從而提高網絡的性能。這種情況發生了很多次，以最小化損失函數的結果，直到它收斂到最小值。這稱為梯度下降。*

我確信這需要解開很多東西。我們來看看一個包含簡單數據集的示例，而不是對每個步驟進行深入研究。

簡單數據的示例

我們的數據集將有 10 個觀察值，其中包含三個特征變量和一個二進制目標變量。X1、X2、X3 和 Y 將表示這些變量。我們將在具有三個層的網絡上訓練這些數據。第一層將有三個節點，代表我們的三個特征變量。下一層（*隱藏層）*將有兩個節點，最后，我們的輸出層中將有一個節點。查看下面的網絡視覺效果：

圖片由作者提供

我們將第一層中的節點表示為 X1、X2 和 X3。在隱藏層中，我們將用 H1 和 H2 表示節點。最后，我們的輸出層將用 Y_hat 表示。

作為參考，我們將使用的數據如下。在這個例子中，我們將前三個觀測值一個一個地通過網絡傳遞，每次傳遞后，我們執行反向傳播并記錄損失函數的收斂性。

圖片由作者提供

第一關

我們的第一個觀測值的每個變量具有以下值：

• X1：1
• X2：10
• X3：5
• Y：0

讓我們將這些插入到第一層的節點中。

圖片由作者提供

請注意這三個節點是如何連接到隱藏層中的第一個節點和第二個節點的。在幕后，我們將執行以下作：

1. 將值代入兩個線性函數（每個節點一個）。我們將用 z1 和 z2 表示輸出
2. 通過 sigmoid 函數（激活函數）傳遞這些線性函數的輸出。我們將用 a1 和 a2 表示它們

讓我們從兩個線性函數開始。在最簡單的形式中，它看起來像這樣：

圖片由作者提供

WX 表示隨機權重和輸入節點值的點積，而 B 表示隨機偏差項。輸入層和隱藏層之間的隨機權重和偏差將是：

• 第一組權重：0.1、0.2、0.3
• 偏差 1：0.1
• 第二組權重 2：0.4、0.5、0.6
• 偏差 2：0.2

現在，讓我們將輸入值代入到每個方程中。請注意，我將第一組權重稱為 w11、w12 和 w13。換句話說，變量中的數字表示它屬于哪組權重以及它在該集中表示的權重。讓我們一步一步地了解 z1。

z1 = （w11 * x1） + （w12 * x2） + （w13 * x3） + b1

• 插入隨機生成的權重和偏差

z1 = （0.1* x1） + （0.2* x2） + （0.3* x3） + 0.1

• 插入輸入值。

z1 = （0.1* 1） + （0.2 * 10） + （0.3 * 5） + 0.1

• 解決

z1 = 3.7

對 z2 進行相同的練習將得到：

z2 = 8.6

我們已經完成了 input 層和 hidden 層之間的連接。下一步是通過激活函數傳遞 z1 和 z2。為什么我們需要引入激活函數？這非常重要;如果沒有激活函數，我們的神經網絡將是一個過于復雜的線性模型。通過激活函數傳遞線性函數的輸出，我們在數據中引入了非線性關系，從而捕獲了線性模型單獨無法發現的復雜性。有幾種不同的激活函數可供選擇，在本文中，我們將使用 ReLU 函數（Rectified Linear Unit）。

圖片由作者提供

在激活函數方面，它沒有比 ReLU 更簡單的了。如果 x 為正，則輸出與 x 相同，否則為 0。ReLU 可以說是隱藏層最流行的激活函數，因為它引入了非線性，提高了計算效率，并減輕了梯度消失（我們將在后面討論）。我們將這些輸出稱為 a1 和 a2。根據我剛才描述的定義，您能否確認第一次傳遞中的 a1 和 a2 會是什么？與 z2 和 z2 相同，因為它們是正數。

A1： 3.7

A2： 8.6

讓我們來看看我們的網絡在第一輪中是什么樣子的。

圖片由作者提供

現在，讓我們完成隱藏層和輸出層之間的橋接。正如我們之前所做的那樣，讓我們獲取隱藏層值，并通過具有隨機權重和偏差項的線性函數傳遞它們。唯一的區別是，除了權重和偏差之外，我們只需要執行一個線性變換，因為我們只處理一個輸出變量。我們將權重和偏差項稱為 hw1 、 hw2 、 hb 和輸出 z3 。

• 隱藏圖層權重：0.7、0.8
• 隱藏層偏差項：0.3

把它們放在一起：

• Z3 = （HW1 * A1） + （HW2 * A2） + HB
• z3 = （0.7 * 3.7） + （0.8 * 8.6） + 0.3
• z3 = 9.77

我們快到了！現在，讓我們將 z3 傳遞給最終的激活函數，這將是 sigmoid 函數。為什么不再使用 ReLU 呢？我們的模型正在使用具有二進制目標變量的數據進行訓練。為了通過反向傳播過程為預測二進制目標的模型調整我們的權重和偏差項，我們需要一個產生概率的激活函數。當我們討論在反向傳播中查找導數的過程時，這將更加清楚。現在，讓我們演示一下 sigmoid 函數的作用：

圖片由作者提供

當我們為 z 代入 9.77 時，我們得到 0.99。換句話說，我們的模型認為這是對 “1” 的非常有把握的預測。在這種情況下，我們的模型當前處于關閉狀態，但這是意料之中的。畢竟，權重和偏差項是在第一次傳遞期間隨機生成的。

圖片由作者提供

無論 z 是什么值，sigmoid 函數的輸出都將是介于 0 和 1 之間的數字。這最終是預測我們的目標變量的原因。一旦我們有了最終模型，任何高于 0.5 的輸出都被預測為“1”，而所有其他輸出被預測為“0”。更重要的是，我們如何使用 sigmoid 函數的輸出通過反向傳播來調整權重和偏置項。現在讓我們談談它。

反向傳播

給我的讀者一個提示：如果你在對所涵蓋的內容有深入的了解的情況下走到了這一步，我必須給你嚴肅的道具。當我第一次了解神經網絡時，我花了很多時間來掌握神經網絡的架構及其所有組件如何協同工作。

現在讓我們深入了解是什么讓神經網絡真正神奇，即反向傳播。這是神經網絡學習和調整權重和偏差項以更好地擬合目標變量的框架。我們結束了第一次傳遞的最終輸出，即 sigmoid 函數產生預測的概率。對于第一個輸出，我們得到 0.99。

反向傳播的第一步是計算損失函數。對于二進制問題，典型的損失函數是二進制交叉熵 （BCE）：

圖片由作者提供

在為這個觀察插入 y 的目標變量并為 y_hat 的 sigmoid 輸出 0.99 之后，我們剩下：

• 損失 = - （0 * log（0.999943） + （1–0） * log（1–0.999943）
• 損失 = - 1 * -log（1–0.999943）
• 虧損 = 9.77

請注意我們如何稱這個變量為 loss。我們的目標是最小化此值。我們很快就會回到這個問題。接下來，讓我們演練一下調整權重和偏差項的過程。

梯度下降

調整我們網絡中的權重和偏差項將通過一個稱為 Gradient Descent 的迭代過程來完成。請看下面的視覺效果。這基本上就是我們在這個過程中要努力實現的目標：

圖片由作者提供

Y 軸表示損失函數的值，而 X 軸代表我們模型中的任何給定權重或偏差。我們可以通過損失函數（二進制交叉熵）實現一個最小值，要找到它，我們必須更改權重和偏置項的迭代值。

最大的問題是，我們如何改變這些值？再看一遍圖表。在圖中，我們只看到一個權重變量 （W）。盡管如此，我們的網絡還有幾個權重和偏差項，因此我們無法從技術上可視化這個過程，因為它將是多個維度。但是，只需在下面使用一個術語即可輕松說明此概念。“星號”是考慮到網絡和數據的結構，我們的損失被最小化到盡可能小的值的地方。當我們開始訓練過程時，理論上該點將在曲線上的位置高得多。如果我們相應地調整權重和偏置項，損失函數應按以下方式變化：

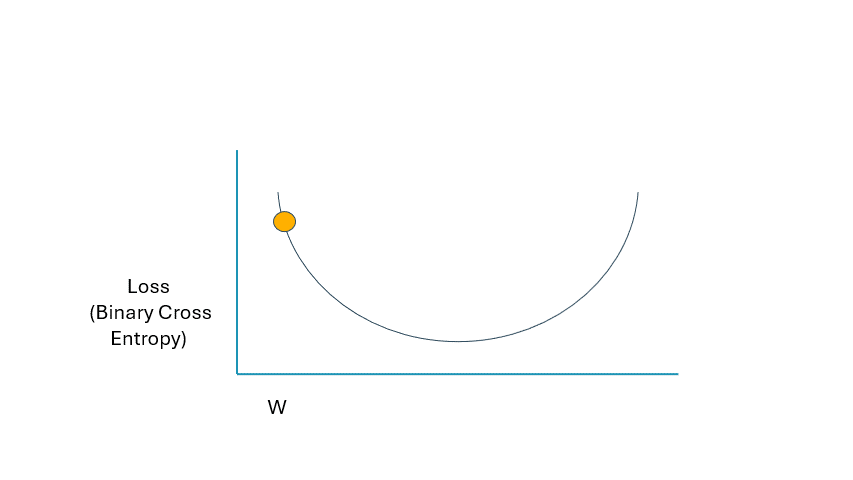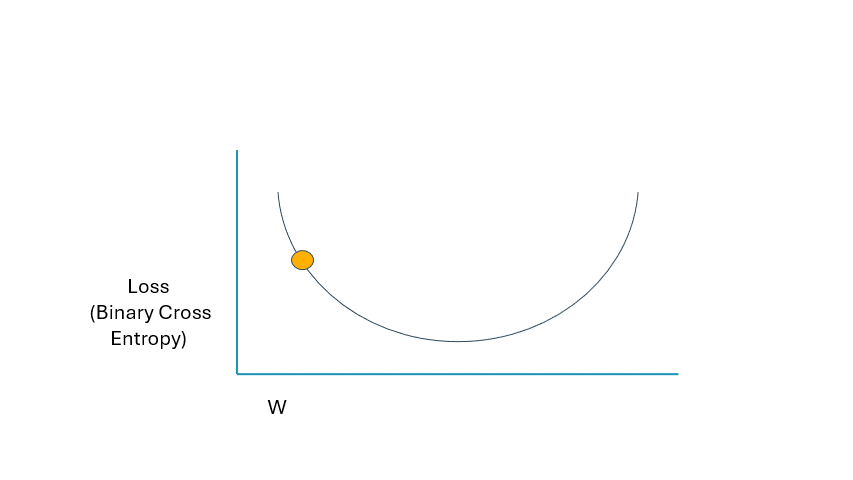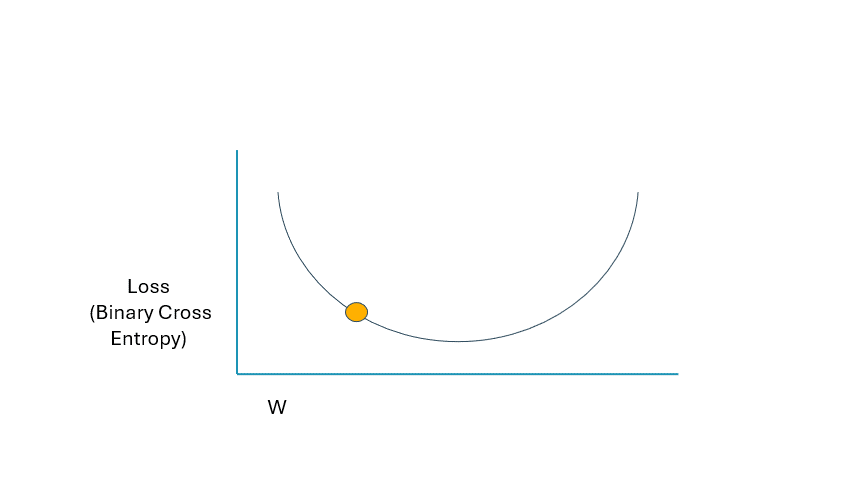
GIF 由作者提供

我們究竟如何更改權重和偏差項？我們現在將深入研究這個問題。

計算梯度和鏈式規則

照片由 卡琳·阿維蒂相 on Unsplash

讓我們回顧一下我們的理論起點。有一條切線向我們顯示網絡的當前斜率。更具體地說，損失函數相對于我們網絡參數的變化速率。這的正式術語是 derivative。當您聽到 derivative 一詞時，請知道它與短語*“change relative to”或“rate of change”*同義。

圖片由作者提供

當我們接近最小值時，請注意導數的變化：

GIF 由作者提供

請注意虛線是如何變得越來越水平的;這意味著導數正在縮小或接近零。這就是我們希望看到的，因為我們執行越來越多的反向傳播。

我們將使用損失函數相對于每個權重和偏差項的導數（梯度）作為調整因子，主要有兩個原因：

• 它揭示了我們需要調整哪個方向以接近最小損失
• 它揭示了我們應該如何調整以接近最小損失的程度。換句話說，絕對值的導數（梯度）越大，我們離最小值就越遠;因此，我們需要以更高的速度進行調整。

此過程有一些注意事項。由于我們不僅更改了一個參數，而且更改了多個參數，因此一次更改所有參數可能會導致我們的損失函數以不穩定的速率變化，這可能導致超過最小值。因此，我們將不斷更新我們的網絡。因此，我們將引入一個介于 0 和 1 之間的學習率，以降低我們調整參數的速率。這個術語更正式地稱為 alpha。

在我們開始調整權重之前，請再看一下網絡的結構。

圖片由作者提供

我們如何進行預測？這對于理解參數的導數計算至關重要。回顧我們網絡的第一次傳遞可能沒有什么壞處。

就在預測之前，我們通過 sigmoid 函數傳遞 z3。為了得到 z3，我們通過具有隨機權重和偏差的線性函數傳遞 a1 和 a2。為了獲得 a1 和 a2，我們將三個輸入變量通過兩個具有隨機權重和偏差的獨立線性函數傳遞，然后通過 ReLU 函數傳遞這兩個輸出。如果你仔細想想，這些參數都以某種方式相互關聯;因此，當一個發生變化時，它會影響其他變化的方式。這使得計算相對于 Loss 的導數有點復雜;但是，理解鏈式規則肯定會澄清這一點。

簡單來說，我們網絡的預測是函數的函數，等等。因此，我們必須將函數鏈接在一起才能正確計算導數。想一想，讓我們以 input 層和 hidden 層之間的橋梁為例。如果我們在第一個線性變換中只調整其中一個權重：

• 它會影響我們通過 ReLU 激活函數傳遞的值。
• 更改我們插入到下一個線性變換中的值
• 更改該線性轉換的輸出
• 更改 sigmoid 激活函數的輸出
• 更改預測。

現在讓我們倒過來工作，我們的第一個任務是找到隱藏層和輸出層之間橋接的權重和偏置項的導數。我們將在下表中進行跟蹤。此外，我們將假設學習率為 0.1

圖片由作者提供

首先，我們必須計算相對于 sigmoid 函數變化的損失變化。請參閱下面的原始表單，并在插入我們之前找到的關聯值后。

圖片由作者提供

接下來，我們將計算 Loss 關于 z3 的導數。請注意前一個導數是如何包含的。這就是鏈式規則的本質。

圖片由作者提供

進一步簡化：

圖片由作者提供

現在我們可以開始計算權重和偏置項的梯度了！現在，我們來求解 loss 相對于輸出層的權重和 bias 的變化。請注意，有三個單獨的方程式，每個方程對應于此特定圖層的每個參數。請記住，我們已經進行了多次計算來獲得其中一些項，因此雖然這些方程看起來相對較短，但仍包含大量內容。另一個需要考慮的注意事項是 z 關于 w1 或 w2 的導數分別只是 a1 和 a2。關于這部分，我最后要注意的是，偏差項以恒定的速率改變 z，因為它沒有加權因子。換句話說，當偏差增加 1 時，z 也會增加。

輸出層 w1：

圖片由作者提供

輸出層 w2：

圖片由作者提供

輸出層偏置：

圖片由作者提供

讓我們重新審視我們的表。以下是我們目前計算的梯度：

圖片由作者提供

我們通過了第一層，還有一層要進行。下一步是計算 Loss 函數相對于 ReLU 激活函數的導數。使用您目前所知道的，您知道這應該是什么樣子嗎？回想一下我們剛剛所做的工作，并考慮 ReLU 函數的輸出在我們的網絡中的位置。

現在，要獲得下一組權重和偏置項，我們首先需要找到損失函數中關于 a1 和 a2 的變化。請注意，z 相對于 a1 和 a2 的變化只是權重 w1 和 w2。

圖片由作者提供

ReLU 函數的兩個調用的輸出都轉到 a1 和 a2。因此，我們需要了解 a1 相對于 ReLU 輸出（我們稱為 z1）的變化，以及 a2 相對于另一個 ReLU 輸出（我們稱為 z2）的變化。它們是 3.7 和 8.6，由于它們只是數字，因此 a1 和 a2 將相對于 z1 和 z2 以 1 的速率變化。話雖如此，關于 z1 和 z2 的損失變化也將是 0.69996 和 0.79995。

現在我們進入最后一組權重和偏差項，更具體地說，我們的隱藏權重和偏差項。此時，我們不是展示所有八個參數的計算，而是演示如何獲得第一個隱藏節點的第一個權重的梯度和該節點的偏置項。碰巧這兩個值都是相同的？您能弄清楚為什么嗎？我們知道 bias 項只是一個數字，因此它只會以恒定的速率改變輸出。另一方面，a1 和隱藏節點 1 權重 1 之間的關系取決于 x1 的值，在本例中為 1。

隱藏節點 1 — 權重 1：

圖片由作者提供

隱藏節點 1 — 偏置項：

圖片由作者提供

現在，我們在第一次通過后有了漸變！它們在這里，請注意，我還包括了學習率調整：

圖片由作者提供

在進入 Python 之前，還有一點要注意 — Batches

我們可以多做幾次調整，但會變得非常重復！相反，讓我們準備好在 Python 中構建自定義神經網絡對象。我想解決的最后一點是在批處理級別更新網絡參數。我剛才向讀者演示的內容表明，您可以在一次傳遞后更新神經網絡中的參數。在現實世界中，情況往往并非如此。相反，大多數數據科學家或機器學習工程師將通過網絡以我們所謂的批處理形式提供許多觀察結果。每次傳遞后，都會計算損失函數。批次結束后，我們計算損失函數的平均值，并使用它來更新參數。

構建神經網絡對象

讓我們從我們的庫和初始化函數開始。以下是有關這些屬性如何工作的一些附加說明。

• **input_size：**這應等于您在數據集中使用的要素數量。
• hidden_layers： 這將是每層中節點數的列表。因此，此列表的長度也將是網絡中隱藏層的數量。
• num_batches： 一個整數，表示每個 epoch 的數據將拆分為的子集數。請記住，在輸入一批中的所有觀測值之前，我們不會調整權重，因此請將其視為在完整數據傳遞中將發生的調整次數。
• 時代： 網絡的完整傳遞次數
• early_stopping_rounds： 在訓練網絡時，我們必須確保沒有對訓練數據進行過擬合。因此，我們將添加一個方法，該方法采用此屬性，并在一定輪數后損失沒有改善時停止訓練。

其余屬性將在我們訓練和初始化模型時填充。

import numpy as np
import pandas as pd
import matplotlib.pyplot as pltclass DIYNeuralNetwork:def __init__(self, input_size, hidden_layers, num_batches, epochs, early_stopping_rounds=None):self.input_size = input_sizeself.hidden_layers = hidden_layersself.num_batches = num_batchesself.epochs = epochsself.early_stopping_rounds = early_stopping_roundsself.layers = []self.train_losses = []self.test_losses = []self._init_weights()

初始化權重和偏差項

雖然我們只是生成隨機項，但讓我們談談它背后的直覺。權重是從正態分布中隨機選擇的，因此它們很可能是介于 -3 到 3 之間的值。此外，我們將它們乘以 0.01，因此典型范圍變為 -0.03 到 0.03。對于偏差項，它們都從 0 開始。

這一切的主要原因是為了防止所謂的梯度爆炸。當梯度足夠大，導致模型開始顯著超過最小損失時，就會發生這種情況。

def _init_weights(self):layer_structure = [self.input_size] + self.hidden_layers + [1]self.weights = []self.biases = []for i in range(len(layer_structure) - 1):weight = np.random.randn(layer_structure[i], layer_structure[i+1]) * 0.01bias = np.zeros(layer_structure[i+1])self.weights.append(weight)self.biases.append(bias)

選擇函數

為 ReLU、ReLU 導數、sigmoid 和 BCE 創建了方法。請注意我們如何為 BCE 添加 epsilon 術語。這確保了我們不會遇到 log（0） 的計算，它等于無窮大。這將導致我們的損失函數中出現 NaN，從而影響我們的模型，使其在訓練期間失敗。

def _relu(self, x):return np.maximum(0, x)def _relu_derivative(self, x):return (x > 0).astype(float)def _sigmoid(self, x):return 1 / (1 + np.exp(-x))def _binary_cross_entropy(self, y_true, y_pred):epsilon = 1e-15  # To avoid log(0)y_pred = np.clip(y_pred, epsilon, 1 - epsilon)return -np.mean(y_true * np.log(y_pred) + (1 - y_true) * np.log(1 - y_pred))

Forward Pass 和 Backpropagation

請注意，在正向傳遞的方法中，“zs”和“activations”是如何記錄的。當我們啟動反向傳播過程時，這一點至關重要。當我們向后工作時，我們將需要這些值來計算導數。

def _forward(self, X):a = np.array(X)activations = [a]zs = []for i in range(len(self.weights)-1):z = a.dot(self.weights[i]) + self.biases[i]a = self._relu(z)zs.append(z)activations.append(a)z = a.dot(self.weights[-1]) + self.biases[-1]a = self._sigmoid(z)zs.append(z)activations.append(a)return activations, zsdef _backward(self, activations, zs, y_true):m = y_true.shape[0]grads_w = [None] * len(self.weights)grads_b = [None] * len(self.biases)# Output layerdelta = activations[-1] - y_truegrads_w[-1] = activations[-2].T.dot(delta) / mgrads_b[-1] = np.mean(delta, axis=0).flatten()# Hidden layersfor i in reversed(range(len(self.hidden_layers))):delta = delta.dot(self.weights[i+1].T) * self._relu_derivative(zs[i])grads_w[i] = activations[i].T.dot(delta) / mgrads_b[i] = np.mean(delta, axis=0)return grads_w, grads_bdef _update_weights(self, grads_w, grads_b, learning_rate):for i in range(len(self.weights)):self.weights[i] -= learning_rate * grads_w[i]self.biases[i] -= learning_rate * grads_b[i]

訓練和預測方法

這就是這一切匯集在一起的地方。還記得我們是如何包含批處理邏輯的嗎？請注意，在每個 epoch 中，我們會先對數據集進行隨機排序，然后再將其劃分為多個批次。這將確保我們不會每次都對訓練數據的相同子集進行訓練。

請注意，當我們使用 predict 函數時，我們是如何調用該方法進行前向傳遞的。更具體地說，我們調用最新的激活值，如果它大于 0.5，我們預測 1;否則為 0。這是因為最后激活值是使用 sigmoid 函數計算的概率。

def train(self, X_train, y_train, X_test, y_test, learning_rate=0.01):best_loss = float('inf')patience = 0for epoch in range(self.epochs):perm = np.random.permutation(len(X_train))X_train = X_train[perm]y_train = y_train[perm]batch_size = len(X_train) // self.num_batchesepoch_train_loss = 0for i in range(self.num_batches):start = i * batch_sizeend = (i + 1) * batch_size if i < self.num_batches - 1 else len(X_train)X_batch = X_train[start:end]y_batch = y_train[start:end]activations, zs = self._forward(X_batch)grads_w, grads_b = self._backward(activations, zs, y_batch)self._update_weights(grads_w, grads_b, learning_rate)epoch_train_loss += self._binary_cross_entropy(y_batch, activations[-1])epoch_train_loss /= self.num_batchesself.train_losses.append(epoch_train_loss)# Evaluate on test settest_pred = self._forward(X_test)[0][-1]epoch_test_loss = self._binary_cross_entropy(y_test, test_pred)self.test_losses.append(epoch_test_loss)if self.early_stopping_rounds:if epoch_test_loss < best_loss:best_loss = epoch_test_losspatience = 0else:patience += 1if patience >= self.early_stopping_rounds:print(f"Early stopping at epoch {epoch+1}")breakprint(f"Epoch {epoch+1} - Train Loss: {epoch_train_loss:.4f} - Test Loss: {epoch_test_loss:.4f}")def predict(self, X):return (self._forward(X)[0][-1] > 0.5).astype(int)

評估、可視化和自定義訓練/測試拆分方法

最后，我們有一個多合一的評估方法，它返回一些我最喜歡的評估指標。一種顯示所有損失函數值的可視化方法。如果您想確定我們的模型是否有效收斂，這一點至關重要。理想情況下，它應該在訓練和測試中顯示損失函數逐漸減少。

def evaluate(self, X, y_true):y_pred = self.predict(X)# Confusion matrix componentstp = np.sum((y_pred == 1) & (y_true == 1))tn = np.sum((y_pred == 0) & (y_true == 0))fp = np.sum((y_pred == 1) & (y_true == 0))fn = np.sum((y_pred == 0) & (y_true == 1))# Metricsaccuracy = (tp + tn) / (tp + tn + fp + fn)precision = tp / (tp + fp + 1e-10)recall = tp / (tp + fn + 1e-10)# Confusion matrix as a dictionaryconfusion_matrix = {'TP': int(tp),'TN': int(tn),'FP': int(fp),'FN': int(fn)}return {'accuracy': accuracy,'precision': precision,'recall': recall,'confusion_matrix': confusion_matrix}def plot_losses(self):plt.plot(self.train_losses, label='Train Loss')plt.plot(self.test_losses, label='Test Loss')plt.xlabel('Epoch')plt.ylabel('Loss')plt.legend()plt.title('Loss Over Epochs')plt.show()@staticmethod
def train_test_split(X, y, test_size=0.2, random_state=None):if random_state:np.random.seed(random_state)indices = np.random.permutation(len(X))split_idx = int(len(X) * (1 - test_size))train_idx, test_idx = indices[:split_idx], indices[split_idx:]return X[train_idx], X[test_idx], y[train_idx], y[test_idx]

Heart Disease 數據示例

讓我們使用 Kaggle 的 heart disease 數據集測試對象。

df = pd.read_csv('heart_2020_cleaned.csv')
df.head()

圖片由作者提供

我們需要通過對所有分類變量進行編碼來清理此數據集。這里要展示的特征有點太多了，但要知道，我們現在數據集中有 39 個特征列。

# Convert Yes/No to binary
df_cleaned_1 = df.replace('Yes', True, regex=True)
df_cleaned_2 = df_cleaned_1.replace('No', False, regex=True)# Identify object/string columns
object_cols = df_cleaned_2.select_dtypes(include=['object', 'string']).columns.tolist()# One-hot encode these columns
encoded_df = pd.get_dummies(df_cleaned_2[object_cols], prefix=object_cols)# Drop the original object columns from df
df_cleaned_prefinal = df_cleaned_2.drop(columns=object_cols)# Concatenate the one-hot encoded columns
df_cleaned_final = pd.concat([df_cleaned_prefinal, encoded_df], axis=1)# Optional: confirm the transformation
print(f"Original object columns: {object_cols}")
print(f"New shape: {df_cleaned_final.shape}")
df_cleaned_final.head()

在進入模型之前，我們先看一下目標類的值計數。注意到什么了嗎？該數據集中的大多數參與者似乎沒有心臟病。在評估模型的性能時，請記住這一點。

df_cleaned_final['HeartDisease'].value_counts()

圖片由作者提供

讓我們創建一個對象的實例并相應地拆分數據。此模型在輸入層中有 39 個節點，在第一個隱藏層中有 20 個節點，在下一層中有 10 個節點。我們將對數據集執行 100 次完整傳遞，并將其分為 10 個批次。如果 10 輪后測試數據集丟失情況沒有改善，訓練作業將停止。最后，我們將學習率設置為 0.1。讓我們開始訓練作業，看看模型的性能如何。

X = df_cleaned_final.drop('HeartDisease', axis=1).astype(np.float32).to_numpy()
y = df_cleaned_final['HeartDisease'].astype(np.float32).to_numpy().reshape(-1, 1)nn = DIYNeuralNetwork(input_size=X.shape[1],hidden_layers=[20, 10],num_batches=10,epochs=100,early_stopping_rounds=10
)X_train, X_test, y_train, y_test = nn.train_test_split(X, y, test_size=0.2, random_state=42)X_train = np.array(X_train)
y_train = np.array(y_train)
X_test = np.array(X_test)
y_test = np.array(y_test)
nn.train(X_train, y_train, X_test, y_test, learning_rate=0.1)

你覺得怎么樣？我們創建了一個強大的模型嗎？它似乎在訓練和測試數據中都有效地收斂了。

nn.plot_losses()

圖片由作者提供

我們實現了 91% 的準確率，這在紙面上聽起來令人印象深刻。看看混淆矩陣。注意到任何有趣的事情了嗎？我們的模型每次都預測負類別。我們的模型并不比僅僅猜測參與者患有心臟病大約 10% 的時間好。

results = nn.evaluate(X_test, y_test)
results

圖片由作者提供

讓我們更上一層樓，讓我們將 epoch 的數量增加到 200，將提前停止增加到 20，看看我們是否能收斂到一組更好的權重和偏差項。

看看結果;該模型的收斂程度似乎略高，但這對其性能沒有影響。我們該怎么辦？我們可以嘗試幾種不同的層、epoch、batch size、learning rate 等組合。

圖片由作者提供

圖片由作者提供

擊打

SMOTE 或合成少數過度采樣技術是一種為少數類的觀察創建合成數據的方法。我不會在這里詳細介紹它是如何工作的;但是，它的基本框架是它選擇 Minority 類的隨機實例，使用 K-Nearest Neighbors 模型確定同一類的最近鄰，并生成位于這些實例之間的合成數據。

一個關鍵的澄清是，我們只對訓練數據應用 SMOTE，因為我們希望確保我們的模型可以在看不見的真實數據上表現良好。讓我們在下面這樣做。如您所見，訓練集中的新類分布為 50/50。

from imblearn.over_sampling import SMOTE# Step 1: Split first
X_train, X_test, y_train, y_test = DIYNeuralNetwork.train_test_split(X, y, test_size=0.2, random_state=42)# Step 2: Apply SMOTE to training data only
smote = SMOTE(random_state=42)
X_train_resampled, y_train_resampled = smote.fit_resample(X_train, y_train.ravel())
y_train_resampled = y_train_resampled.reshape(-1, 1)# Confirm new class distribution
print("Class distribution after SMOTE:", np.bincount(y_resampled.flatten().astype(int)))

圖片由作者提供

我進行了一些試驗和錯誤并調整了模型的參數。除了結果之外，還可以在下面查看它們。注意到任何有趣的事情了嗎？如果您查看損失圖，您可以看到一個非常健康的趨勢，即最大限度地減少損失，甚至似乎還有進一步的改進空間。準確性確實有所下降，但我們的模型現在已經證明了預測正類實例的能力。這是個好消息。為什么？這是一個理論上可以用來預測某人是否有患心臟病風險的模型，所以讓我們考慮一下預測的場景：

• （真陽性）我們告訴某人**他們患有心臟病，而他們也患有**心臟病。
• （真陰性）我們告訴某人他們**沒有心臟病，他們也沒有**心臟病。
• （誤報）我們告訴某人**他們患有心臟病，而他們沒有**心臟病。
• （假陰性）我們告訴某人他們**沒有心臟病，他們確實患有**心臟病。

在這些選項中，我們應該尋求最小化或最大化什么？我不知道你是怎么想的，但在這種情況下的假陰性對個人來說是災難性的。想象一下，如果我們告訴他們他們沒有患心臟病的風險，并且他們不做任何改變就過自己的生活。作為數據科學家，我們必須認真對待這些情況。在這種情況下，我們必須確保獲得盡可能高的召回分數，因為它可以最大限度地減少假陰性。

# Initialize and train
nn = DIYNeuralNetwork(input_size=X_train_resampled.shape[1],hidden_layers=[20],num_batches=10,epochs=200,early_stopping_rounds=30)nn.train(X_train_resampled, y_train_resampled, X_test, y_test, learning_rate=0.01)

圖片由作者提供