目錄
一、斐波那契數列(兔子問題)
二、迭代法(用while循環推下一項 )
三、遞歸函數
(函數的定義中調用函數自身的一種函數定義方式)?
四、遞歸函數的底層邏輯推理
(二叉樹推倒最左下節點回退法)
一、斐波那契數列(兔子問題)
學習遞歸函數,分析遞歸流程。
斐波那契是中世紀一個有名的數學家,他在計算之書中提出了一個有趣的:
兔子問題:
# 若一對成年兔子,每個月生下一對小兔子,恰好一雌一雄。
# 在年初時,只有一對小兔子。
# 第1個月結束時,他們成長為成年兔子。
# 第2個月結束時,這對成年兔子,則生下一對小兔子。
# 這種成長與繁殖過程一直持續下去,并假設生下的小兔子不會死,那么一年之后將會有多少只兔子?
# 推算第5個月兔子總數。#第1個月:1對兔子。
#第2個月:小兔子長大,仍然1對兔子。
#第3個月:這對兔子生了1對小兔子,所以有2對兔子。
#第4個月:老兔子又生了1對兔子,而上個月新出生的兔子還未成熟,所以有3對兔子。
#第5個月:這是已經有2對兔子可以繁殖,于是生了2對兔子。所以有5對兔子。#第n個月的兔子總數=第n-1個月的兔子總數+第n-2個月的兔子總數
#斐波那契數列(黃金分割):1,1,2,3,5,8,13,21,34,55...
#取出最后得到的兩個數,取出21和34,21÷34約等于0.618,是黃金分割比例。
二、迭代法(用while循環推下一項 )
#用while循環推倒斐波那契數列下一項:
#斐波那切數列:假如這個函數可以生成斐波那切數列第n項:
#例如:0,1,1,2,3,5,8,13,21,34,55...
#fibo(0)=0,fibo(1)=1,fibo(2)=1;
#當fibo(n)時,返回就是斐波那切數列對應的第n項。
def fibo(n):#斐波那切數列的前兩項是:0,1fibo_list=[0,1]##**變量ii=2#讓列表包括斐波那切的所有數字,直到第n項,寫while循環。while i<=n:##每次推導出數列的下一個數值num(第i項第值num,規律)num=fibo_list[i-1]+fibo_list[i-2]# append方法添加到列表的最后fibo_list.append(num)#添加到最后一項循環結束##加1操作i+=1#返回斐波那契額數列第n項return fibo_list[n]#因為數列第0,1項已知,所以添加第2項到數列,變量i
#1.打印第5項
print(fibo(5))
#2.打印0-10項
# for j in range(10):
#???? print(fibo(j))? #打印前10項#遞歸函數:def funA():
#在函數內部可以調用其他函數,如果一個函數直接或者間接調用函數本身,是遞歸函數
三、遞歸函數
(函數的定義中調用函數自身的一種函數定義方式)?
# f(0)=0
# f(1)=1
# f(2)=1=0+1=f(1)+f(0)
# f(3)=2=1+1=f(2)+f(1)#f(n)=f(n-1)+f(n-2)def fibo(n):if n==0:return 0elif n==1:return 1# if n<2:#???? return nelse:return fibo(n-1)+fibo(n-2)? #函數內調用了這個,所以遞歸for j in range(10):print(fibo(j))四、遞歸函數的底層邏輯推理
(二叉樹推倒最左下節點回退法)
#定義簡單,邏輯清晰
#過程中發生了什么,樹形圖
def fibo(n):print('fibo:'+str(n))if n<2:return nelse:return fibo(n-1) + fibo(n-2)
print(fibo(3))
#print(fibo(6))?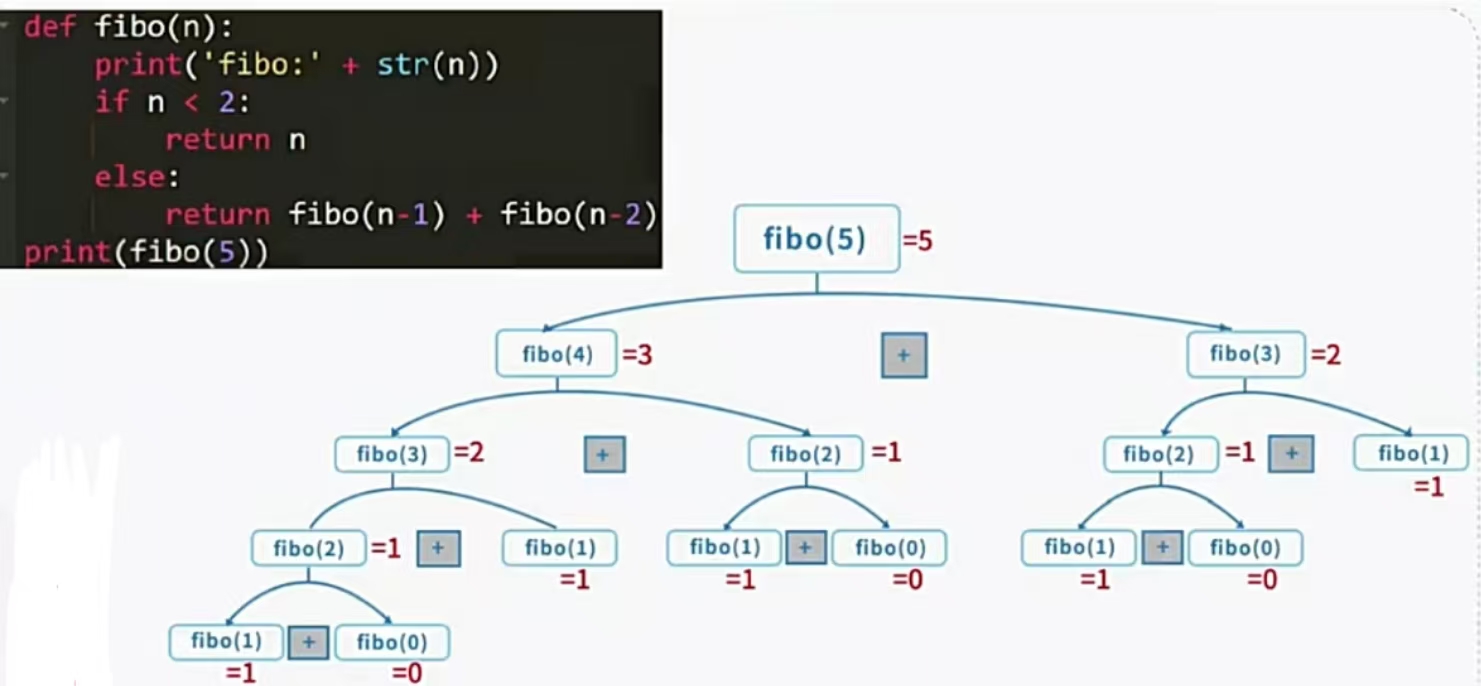

)

)







)





)
——設計思路、實現步驟、代碼實現)

